6.3.7一元一次方程-面积周长问题 同步练习 2021—2022学年华东师大版数学七年级下册
文档属性
| 名称 | 6.3.7一元一次方程-面积周长问题 同步练习 2021—2022学年华东师大版数学七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 278.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-02 14:36:05 | ||
图片预览



文档简介
6.3.7一元一次方程-面积周长问题
一.选择题(共6小题)
1.内径为120mm的圆柱形玻璃杯,和内径为300mm,内高为32mm的圆柱形玻璃盆可以盛同样多的水,则玻璃杯的内高为( )
A.150mm B.200mm C.250mm D.300mm
2.在矩形ABCD中放入六个长、宽都相同的小长方形,所标尺寸如图所示,求小长方形的宽AE.若AE=x(cm),依题意可得方程( )
A.6+2x=14﹣3x B.6+2x=x+(14﹣3x)
C.14﹣3x=6 D.6+2x=14﹣x
3.一梯形面积为84cm2,高为8cm,它的下底比上底的2倍少3cm,求这个梯形的上底和下底的长度.解题时设梯形的上底为xcm,那么下面正确的方程是( )
A.8[x+(2x+3)]=84 B.8[x+(2x﹣3)]=84
C.×8[x+(2x+3)]=84 D.×8×[x+(2x﹣3)]=84
4.甲、乙两个油桶中装有体积相等的油.先把甲桶的油倒一半到乙桶(乙桶没有溢出),再把乙桶的油倒出给甲桶(甲桶没有溢出),这时两个油桶中的油的是( )
A.甲桶的油多
B.乙桶的油多
C.甲桶与乙桶一样多
D.无法判断,与原有的油的体积大小有关
5.要锻造直径为2厘米,高为16厘米的圆柱形机器零件10件,则需直径为4厘米的圆钢柱长( )
A.10厘米 B.20厘米 C.30厘米 D.40厘米
6.六张形状大小完全相同的小长方形(白色部分)如图摆放在大长方形ABCD中,BC=n,AB=m,则图中两块阴影部分长方形的周长和是( )
A.4m B.4n C.2(m+n) D.4(m﹣n)
二.填空题(共6小题)
7.一个长方体水箱,从里面量长、宽、高分别为40cm、30cm和30cm,箱中水面高10cm,放进一个棱长为20cm的正方体铁块后,这时水面高为 cm.
8.如图,一块长4厘米、宽1厘米的长方形纸板①,一块长5厘米、宽2厘米的长方形纸板②与一块正方形纸板③以及另两块长方形纸板④和⑤,恰好拼成一个大正方形,则大正方形的面积是 平方厘米.
9.李红用40cm长的铁丝围成一个长方形,要使长方形的长比宽多4cm.设宽为xcm,则可列方程为 ,围成的长方形的面积为 .
10.有一艘轮船的载重量是800吨,容积是795立方米.现要装运生铁和棉花两种物资,生铁每吨的体积为0.3立方米,棉花每吨的体积为4立方米,则生铁装 吨、棉花装 吨才能充分利用船的载重量和容积.
11.现有含盐30%的盐水60千克,要把它变成浓度为40%的盐水,有下列两种方案:
(1)加盐,问需盐多少千克?若设需加盐x千克,所列方程为 ,求得x= .
(2)蒸发水,问需蒸发多少千克?若设需蒸发y千克,所列方程为 ,求得y= .
12.实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在容器的5cm高度处连通(即管子底离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升cm.
(1)开始注水1分钟,丙的水位上升 cm.
(2)开始注入 分钟的水量后,乙的水位比甲高0.5cm.
三.解答题(共8小题)
13.在一个底面直径为5cm,高为16cm圆柱形瓶内装满水,再将瓶内的水倒入一个底面直径为6cm,高为10cm的圆柱形玻璃杯中,能否完全装下?若装不下,求瓶内水面还有多高?若未能装满,求玻璃杯内水面离杯口的距离?
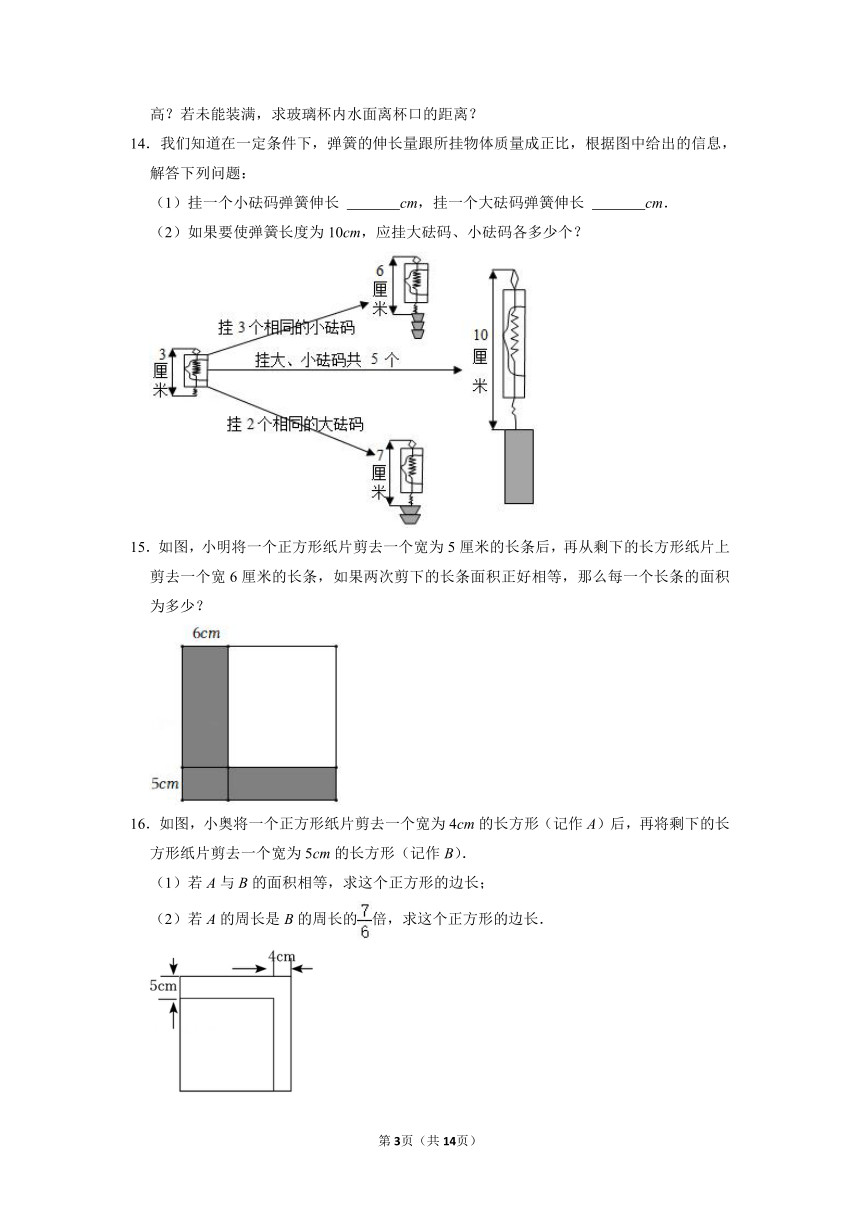
14.我们知道在一定条件下,弹簧的伸长量跟所挂物体质量成正比,根据图中给出的信息,解答下列问题:
(1)挂一个小砝码弹簧伸长 cm,挂一个大砝码弹簧伸长 cm.
(2)如果要使弹簧长度为10cm,应挂大砝码、小砝码各多少个?
15.如图,小明将一个正方形纸片剪去一个宽为5厘米的长条后,再从剩下的长方形纸片上剪去一个宽6厘米的长条,如果两次剪下的长条面积正好相等,那么每一个长条的面积为多少?
16.如图,小奥将一个正方形纸片剪去一个宽为4cm的长方形(记作A)后,再将剩下的长方形纸片剪去一个宽为5cm的长方形(记作B).
(1)若A与B的面积相等,求这个正方形的边长;
(2)若A的周长是B的周长的倍,求这个正方形的边长.
17.一个长方形养鸡场的长边靠墙,墙长14米,其他三边用竹篱笆围成,现有长为35米的篱笆,爸爸的设计方案是长比宽多5米;妈妈的设计方案是长比宽多2米,你认为谁的设计合理,为什么?如果按这种设计,养鸡场的面积是多少?
18.如图,是一块在电脑屏幕上出现的矩形色块图,由6个颜色不同的正方形组成,设中间最小的一个正方形边长为1,求这个矩形色块图的面积.
19.张师傅想用篱笆围一个长方形鸡舍,一边利用房屋外的一面墙(墙的长度为12米),其他三边用篱笆,且中间用篱笆隔开,并在如图位置开两扇宽各1米的门(门不用篱笆),若鸡舍的宽为(a+2)米,长比宽的还多1米.
(1)求所用篱笆的总长度是多少米?(用含a的代数式表示,且结果要化简)
(2)当所围成的鸡舍用去篱笆的总长度为21米时,求a的值;
(3)能用27.6米长的篱笆围成符合条件的鸡舍吗?若能围成,求出此时的a值;若不能围成,请说明理由.
20.如图,A、B两点在数轴上对应的数分别为﹣20、40,在A、B两点处各放一个挡板,M、N两个电子小球同时从原点出发,M以2个单位/秒的速度向数轴负方向运动,N以4个单位/秒的速度向数轴正方向运动,碰到挡板后则反方向运动,速度大小不变,当两小球第一次相遇时都停止运动.设两个小球运动的时间为t,那么:
(1)当0<t<10时,M在数轴上对应的数可以表示为 ;
(2)小杨同学发现:当0<t<10时,2MB﹣NA始终为定值.小杨的发现是否正确?若正确,请求出这个定值;若不正确,请说明理由.
(3)在整个运动过程中,t为何值时M、N两个小球间的距离为6?请直接写出答案.
6.3.7一元一次方程-面积周长问题
参考答案与试题解析
一.选择题(共6小题)
1.内径为120mm的圆柱形玻璃杯,和内径为300mm,内高为32mm的圆柱形玻璃盆可以盛同样多的水,则玻璃杯的内高为( )
A.150mm B.200mm C.250mm D.300mm
【解答】解:设玻璃杯内高为x,
依据题意得:π×x=π×32解得x=200mm,
故选:B.
2.在矩形ABCD中放入六个长、宽都相同的小长方形,所标尺寸如图所示,求小长方形的宽AE.若AE=x(cm),依题意可得方程( )
A.6+2x=14﹣3x B.6+2x=x+(14﹣3x)
C.14﹣3x=6 D.6+2x=14﹣x
【解答】解:设AE为xcm,则AM为(14﹣3x)cm,
根据题意得出:∵AN=MW,∴AN+6=x+MR,
即6+2x=x+(14﹣3x)
故选:B.
3.一梯形面积为84cm2,高为8cm,它的下底比上底的2倍少3cm,求这个梯形的上底和下底的长度.解题时设梯形的上底为xcm,那么下面正确的方程是( )
A.8[x+(2x+3)]=84 B.8[x+(2x﹣3)]=84
C.×8[x+(2x+3)]=84 D.×8×[x+(2x﹣3)]=84
【解答】解:设梯形的上底为xcm,则下底为:(2x﹣3)cm,根据题意得出:
(x+2x﹣3)×8=84.
故选:D.
4.甲、乙两个油桶中装有体积相等的油.先把甲桶的油倒一半到乙桶(乙桶没有溢出),再把乙桶的油倒出给甲桶(甲桶没有溢出),这时两个油桶中的油的是( )
A.甲桶的油多
B.乙桶的油多
C.甲桶与乙桶一样多
D.无法判断,与原有的油的体积大小有关
【解答】解:设甲、乙两个油桶中油的重量为a.根据题意,得:
因为先把甲桶的油倒一半至乙桶,
甲桶的油=(1﹣)a,乙桶的油=(1+)a,
再把乙桶的油倒出三分之一给甲桶,
所以甲桶有油(1﹣)a+(1+)a×=a,
乙桶有油(1+) a (1﹣)=a,
所以甲乙两桶油一样多.
故选:C.
5.要锻造直径为2厘米,高为16厘米的圆柱形机器零件10件,则需直径为4厘米的圆钢柱长( )
A.10厘米 B.20厘米 C.30厘米 D.40厘米
【解答】解:设应截取直径4厘米的圆钢x厘米,
由题意得:π×()2×16×10=π×()2 x
解得:x=40.
故选:D.
6.六张形状大小完全相同的小长方形(白色部分)如图摆放在大长方形ABCD中,BC=n,AB=m,则图中两块阴影部分长方形的周长和是( )
A.4m B.4n C.2(m+n) D.4(m﹣n)
【解答】解:如图
由题意:EF=BM,HK=GD.
∴两个阴影部分长方形的四个长的和为AG+HK+CM+EF=AG+GD+BM+CM=AD+BC=2n.
设小白长方形的长为x,宽为y,则AE=GF=m﹣3y,CK=HM=m﹣x.
∴两个阴影部分长方形的四个宽的和为2AE+2CK=2(m﹣3y)+2(m﹣x)=4m﹣2(x+3y).
∵BM=x,CM=3y.
∴x+3y=BM+CM=BC=n.
∴两个阴影部分长方形的四个宽的和为4m﹣2n.
∴两块阴影部分长方形的周长和是2n+4m﹣2n=4m.
故选:A.
二.填空题(共6小题)
7.一个长方体水箱,从里面量长、宽、高分别为40cm、30cm和30cm,箱中水面高10cm,放进一个棱长为20cm的正方体铁块后,这时水面高为 15 cm.
【解答】解:设放入正方体铁块后水面高为h厘米,由题意得:
40×30×10+20×20×h=40×30×h,
解得:h=15.
答:这时水面高15厘米.
故答案为:15.
8.如图,一块长4厘米、宽1厘米的长方形纸板①,一块长5厘米、宽2厘米的长方形纸板②与一块正方形纸板③以及另两块长方形纸板④和⑤,恰好拼成一个大正方形,则大正方形的面积是 36 平方厘米.
【解答】解:设小正方形的边长为x,依题意得
1+x+2=4+5﹣x,
解得x=3,
∴大正方形的边长为6厘米,
∴大正方形的面积是6×6=36(平方厘米),
答:大正方形的面积是36平方厘米.
故答案是:36.
9.李红用40cm长的铁丝围成一个长方形,要使长方形的长比宽多4cm.设宽为xcm,则可列方程为 2(x+4+x)=40 ,围成的长方形的面积为 96cm2 .
【解答】解:设这个长方形的宽为xcm,则长为(x+4)cm,
则可列方程:2(x+4+x)=40,
解得:x=8,
围成的长方形的面积为8×12=96(cm2),
故答案为:2(x+4+x)=40,96cm2.
10.有一艘轮船的载重量是800吨,容积是795立方米.现要装运生铁和棉花两种物资,生铁每吨的体积为0.3立方米,棉花每吨的体积为4立方米,则生铁装 650 吨、棉花装 150 吨才能充分利用船的载重量和容积.
【解答】解:设生铁运x吨,则棉花运(800﹣x)吨,
由题意得出:0.3x+4(800﹣x)=795,
解得:x=650,
800﹣650=150(吨),
答:生铁运650吨,棉花运150吨,
故答案为:650;150.
11.现有含盐30%的盐水60千克,要把它变成浓度为40%的盐水,有下列两种方案:
(1)加盐,问需盐多少千克?若设需加盐x千克,所列方程为 60(1﹣10%)=(60+x)(1﹣40%) ,求得x= 30 .
(2)蒸发水,问需蒸发多少千克?若设需蒸发y千克,所列方程为 60×30%=(60﹣y)×40% ,求得y= 15 .
【解答】解:(1)设需要加盐x千克,
由题意得:60(1﹣10%)=(60+x)(1﹣40%).
解得 x=30
故答案是:60(1﹣10%)=(60+x)(1﹣40%);30;
(2)设需蒸发y千克,
由题意得:60×30%=(60﹣y)×40%
解得y=15.
故答案是:60×30%=(60﹣y)×40%;15.
12.实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在容器的5cm高度处连通(即管子底离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升cm.
(1)开始注水1分钟,丙的水位上升 cm.
(2)开始注入 或 分钟的水量后,乙的水位比甲高0.5cm.
【解答】解:(1)∵甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,
∵注水1分钟,乙的水位上升cm,
∴得到注水1分钟,丙的水位上升cm×4=cm;
(2)设开始注入t分钟的水量后,乙的水位比甲高0.5cm,有两种情况:
①甲的水位不变时;
由题意得,t﹣1=0.5,
解得:t=,
∵×=6>5,
∴此时丙容器已向乙容器溢水,
∵5÷=分钟,×=,即经过分钟时丙容器的水到达管子底部,乙的水位上升,
∴+2×(t﹣)﹣1=0.5,解得:t=;
②当乙的水位到达管子底部,甲的水位上升时,
∵乙的水位到达管子底部的时间为;+(5﹣)÷÷2=分钟,
∴5﹣1﹣2×(t﹣)=0.5,
解得:t=,
综上所述开始注入或分钟的水量后,乙的水位比甲高0.5cm.
故答案为cm;或.
三.解答题(共8小题)
13.在一个底面直径为5cm,高为16cm圆柱形瓶内装满水,再将瓶内的水倒入一个底面直径为6cm,高为10cm的圆柱形玻璃杯中,能否完全装下?若装不下,求瓶内水面还有多高?若未能装满,求玻璃杯内水面离杯口的距离?
【解答】解:设将瓶内的水倒入一个底面直径是6cm,高是10cm的圆柱形玻璃杯中时,水面高为xcm,
根据题意得π ()2 x=π ()2×16,
解得x=,
∵>10,
∴不能完全装下.
﹣10=(cm),
16×=1.6(cm),
答:装不下,那么瓶内水面还有1.6cm.
14.我们知道在一定条件下,弹簧的伸长量跟所挂物体质量成正比,根据图中给出的信息,解答下列问题:
(1)挂一个小砝码弹簧伸长 1 cm,挂一个大砝码弹簧伸长 2 cm.
(2)如果要使弹簧长度为10cm,应挂大砝码、小砝码各多少个?
【解答】解:(1)由图可知:挂一个小砝码弹簧伸长(6﹣3)÷3=1(cm),
挂一个大砝码弹簧伸长(7﹣3)÷2=2(cm),
故答案为:1,2;
(2)设应挂大砝码x个,则小砝码(5﹣x)个,
根据题意得:2x+(5﹣x)×1=10﹣3,
解得:x=2,
∴5﹣x=5﹣2=3,
答:应挂大砝码2个,小砝码3个.
15.如图,小明将一个正方形纸片剪去一个宽为5厘米的长条后,再从剩下的长方形纸片上剪去一个宽6厘米的长条,如果两次剪下的长条面积正好相等,那么每一个长条的面积为多少?
【解答】解:设原来正方形纸的边长是xcm,则第一次剪下的长条的长是xcm,宽是5cm,第二次剪下的长条的长是(x﹣5)cm,宽是6cm,
由题意得:5x=6(x﹣5),
解得:x=30,
则30×5=150(cm2).
答:每一个长条的面积为150cm2.
16.如图,小奥将一个正方形纸片剪去一个宽为4cm的长方形(记作A)后,再将剩下的长方形纸片剪去一个宽为5cm的长方形(记作B).
(1)若A与B的面积相等,求这个正方形的边长;
(2)若A的周长是B的周长的倍,求这个正方形的边长.
【解答】解:(1)设正方形的边长为xcm,
由题意,得4x=5(x﹣4).
解得x=20.
答:这个正方形的边长为20cm;
(2)设这个正方形的边长为ycm,
由题意,得6(2y+8)=7×2[5+(y﹣4)].
解得y=17.
答:这个正方形的边长为17cm.
17.一个长方形养鸡场的长边靠墙,墙长14米,其他三边用竹篱笆围成,现有长为35米的篱笆,爸爸的设计方案是长比宽多5米;妈妈的设计方案是长比宽多2米,你认为谁的设计合理,为什么?如果按这种设计,养鸡场的面积是多少?
【解答】解:设爸爸的设计方案中鸡场的宽为xm,则长为(x+5)m,
根据题意得:2x+(x+5)=35,
解得:x=10,
x+5=15m>14m,所以不符合实际;
设妈妈的设计方案中鸡场的宽为ym,则长为(y+2)m,
根据题意得:2y+(y+2)=35,
解得:y=11,
y+2=13m<14m,所以符合实际,
此时鸡场的面积为11×13=143m2,
答:妈妈的设计符合实际,鸡场的面积为143m2.
18.如图,是一块在电脑屏幕上出现的矩形色块图,由6个颜色不同的正方形组成,设中间最小的一个正方形边长为1,求这个矩形色块图的面积.
【解答】解:如图所示
DF﹣AE=1,AE=BE+1,2CF﹣DF=1
DF=AE+1,AE=CF+1+1,DF=CF+3,
2CF﹣CF﹣3=1,解得CF=4,
∴BE=5,AE=6,∴AB=11,BC=13
S=AB BC=11×13=143.
19.张师傅想用篱笆围一个长方形鸡舍,一边利用房屋外的一面墙(墙的长度为12米),其他三边用篱笆,且中间用篱笆隔开,并在如图位置开两扇宽各1米的门(门不用篱笆),若鸡舍的宽为(a+2)米,长比宽的还多1米.
(1)求所用篱笆的总长度是多少米?(用含a的代数式表示,且结果要化简)
(2)当所围成的鸡舍用去篱笆的总长度为21米时,求a的值;
(3)能用27.6米长的篱笆围成符合条件的鸡舍吗?若能围成,求出此时的a值;若不能围成,请说明理由.
【解答】解:(1)∵鸡舍的宽为(a+2)米,长比宽的还多1米,
∴鸡舍的长为(a+2)+1米,
∵两扇小门宽各2米,
∴篱笆的总长度L=3×鸡舍的宽度+鸡舍的长度﹣2×小门的宽度=3(a+2)+[(a+2)+1]﹣2×1=;
(2)将L=21代入L=得:=21,解得:a=2;
(3)将L=27.6代入L=得:=27.6,
解得:a=3.2,
当a=3.2时,鸡舍的宽度为(3.2+2)+1=14>12,
故27.6米的篱笆不能围成符合题意的鸡舍.
20.如图,A、B两点在数轴上对应的数分别为﹣20、40,在A、B两点处各放一个挡板,M、N两个电子小球同时从原点出发,M以2个单位/秒的速度向数轴负方向运动,N以4个单位/秒的速度向数轴正方向运动,碰到挡板后则反方向运动,速度大小不变,当两小球第一次相遇时都停止运动.设两个小球运动的时间为t,那么:
(1)当0<t<10时,M在数轴上对应的数可以表示为 ﹣2t ;
(2)小杨同学发现:当0<t<10时,2MB﹣NA始终为定值.小杨的发现是否正确?若正确,请求出这个定值;若不正确,请说明理由.
(3)在整个运动过程中,t为何值时M、N两个小球间的距离为6?请直接写出答案.
【解答】解:(1)M、N碰到挡板所需时间均为10s,
∴0<t<10时M未碰到挡板运动距离为2t,又M向负轴运动,则M对应数轴上的数为﹣2t,
故答案为﹣2t.
(2)0<t<10时,设O点在数轴上对应的数为0,
则MB=MO+OB=2t+40;NA=NO+OA=4t+20,
2MB﹣NA=2(2t+40)﹣(4t+20)=60,
故2MB﹣NA为定值,定值为60.
(3)0<t<10时,MN=MO+ON=2t+4t=6t,令MN=6则t=l;
10<t<20时,MN=MO+ON=AO﹣AM+BO﹣BN=20﹣(2t﹣20)+40﹣(4t﹣40)=120﹣6t;
令MN=6则t=19.
故t=1s或19s时,MN两个小球间距离为6.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2022/3/23 14:02:32;用户:杨晓忆;邮箱:syx071@;学号:24369258
第1页(共14页)
一.选择题(共6小题)
1.内径为120mm的圆柱形玻璃杯,和内径为300mm,内高为32mm的圆柱形玻璃盆可以盛同样多的水,则玻璃杯的内高为( )
A.150mm B.200mm C.250mm D.300mm
2.在矩形ABCD中放入六个长、宽都相同的小长方形,所标尺寸如图所示,求小长方形的宽AE.若AE=x(cm),依题意可得方程( )
A.6+2x=14﹣3x B.6+2x=x+(14﹣3x)
C.14﹣3x=6 D.6+2x=14﹣x
3.一梯形面积为84cm2,高为8cm,它的下底比上底的2倍少3cm,求这个梯形的上底和下底的长度.解题时设梯形的上底为xcm,那么下面正确的方程是( )
A.8[x+(2x+3)]=84 B.8[x+(2x﹣3)]=84
C.×8[x+(2x+3)]=84 D.×8×[x+(2x﹣3)]=84
4.甲、乙两个油桶中装有体积相等的油.先把甲桶的油倒一半到乙桶(乙桶没有溢出),再把乙桶的油倒出给甲桶(甲桶没有溢出),这时两个油桶中的油的是( )
A.甲桶的油多
B.乙桶的油多
C.甲桶与乙桶一样多
D.无法判断,与原有的油的体积大小有关
5.要锻造直径为2厘米,高为16厘米的圆柱形机器零件10件,则需直径为4厘米的圆钢柱长( )
A.10厘米 B.20厘米 C.30厘米 D.40厘米
6.六张形状大小完全相同的小长方形(白色部分)如图摆放在大长方形ABCD中,BC=n,AB=m,则图中两块阴影部分长方形的周长和是( )
A.4m B.4n C.2(m+n) D.4(m﹣n)
二.填空题(共6小题)
7.一个长方体水箱,从里面量长、宽、高分别为40cm、30cm和30cm,箱中水面高10cm,放进一个棱长为20cm的正方体铁块后,这时水面高为 cm.
8.如图,一块长4厘米、宽1厘米的长方形纸板①,一块长5厘米、宽2厘米的长方形纸板②与一块正方形纸板③以及另两块长方形纸板④和⑤,恰好拼成一个大正方形,则大正方形的面积是 平方厘米.
9.李红用40cm长的铁丝围成一个长方形,要使长方形的长比宽多4cm.设宽为xcm,则可列方程为 ,围成的长方形的面积为 .
10.有一艘轮船的载重量是800吨,容积是795立方米.现要装运生铁和棉花两种物资,生铁每吨的体积为0.3立方米,棉花每吨的体积为4立方米,则生铁装 吨、棉花装 吨才能充分利用船的载重量和容积.
11.现有含盐30%的盐水60千克,要把它变成浓度为40%的盐水,有下列两种方案:
(1)加盐,问需盐多少千克?若设需加盐x千克,所列方程为 ,求得x= .
(2)蒸发水,问需蒸发多少千克?若设需蒸发y千克,所列方程为 ,求得y= .
12.实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在容器的5cm高度处连通(即管子底离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升cm.
(1)开始注水1分钟,丙的水位上升 cm.
(2)开始注入 分钟的水量后,乙的水位比甲高0.5cm.
三.解答题(共8小题)
13.在一个底面直径为5cm,高为16cm圆柱形瓶内装满水,再将瓶内的水倒入一个底面直径为6cm,高为10cm的圆柱形玻璃杯中,能否完全装下?若装不下,求瓶内水面还有多高?若未能装满,求玻璃杯内水面离杯口的距离?
14.我们知道在一定条件下,弹簧的伸长量跟所挂物体质量成正比,根据图中给出的信息,解答下列问题:
(1)挂一个小砝码弹簧伸长 cm,挂一个大砝码弹簧伸长 cm.
(2)如果要使弹簧长度为10cm,应挂大砝码、小砝码各多少个?
15.如图,小明将一个正方形纸片剪去一个宽为5厘米的长条后,再从剩下的长方形纸片上剪去一个宽6厘米的长条,如果两次剪下的长条面积正好相等,那么每一个长条的面积为多少?
16.如图,小奥将一个正方形纸片剪去一个宽为4cm的长方形(记作A)后,再将剩下的长方形纸片剪去一个宽为5cm的长方形(记作B).
(1)若A与B的面积相等,求这个正方形的边长;
(2)若A的周长是B的周长的倍,求这个正方形的边长.
17.一个长方形养鸡场的长边靠墙,墙长14米,其他三边用竹篱笆围成,现有长为35米的篱笆,爸爸的设计方案是长比宽多5米;妈妈的设计方案是长比宽多2米,你认为谁的设计合理,为什么?如果按这种设计,养鸡场的面积是多少?
18.如图,是一块在电脑屏幕上出现的矩形色块图,由6个颜色不同的正方形组成,设中间最小的一个正方形边长为1,求这个矩形色块图的面积.
19.张师傅想用篱笆围一个长方形鸡舍,一边利用房屋外的一面墙(墙的长度为12米),其他三边用篱笆,且中间用篱笆隔开,并在如图位置开两扇宽各1米的门(门不用篱笆),若鸡舍的宽为(a+2)米,长比宽的还多1米.
(1)求所用篱笆的总长度是多少米?(用含a的代数式表示,且结果要化简)
(2)当所围成的鸡舍用去篱笆的总长度为21米时,求a的值;
(3)能用27.6米长的篱笆围成符合条件的鸡舍吗?若能围成,求出此时的a值;若不能围成,请说明理由.
20.如图,A、B两点在数轴上对应的数分别为﹣20、40,在A、B两点处各放一个挡板,M、N两个电子小球同时从原点出发,M以2个单位/秒的速度向数轴负方向运动,N以4个单位/秒的速度向数轴正方向运动,碰到挡板后则反方向运动,速度大小不变,当两小球第一次相遇时都停止运动.设两个小球运动的时间为t,那么:
(1)当0<t<10时,M在数轴上对应的数可以表示为 ;
(2)小杨同学发现:当0<t<10时,2MB﹣NA始终为定值.小杨的发现是否正确?若正确,请求出这个定值;若不正确,请说明理由.
(3)在整个运动过程中,t为何值时M、N两个小球间的距离为6?请直接写出答案.
6.3.7一元一次方程-面积周长问题
参考答案与试题解析
一.选择题(共6小题)
1.内径为120mm的圆柱形玻璃杯,和内径为300mm,内高为32mm的圆柱形玻璃盆可以盛同样多的水,则玻璃杯的内高为( )
A.150mm B.200mm C.250mm D.300mm
【解答】解:设玻璃杯内高为x,
依据题意得:π×x=π×32解得x=200mm,
故选:B.
2.在矩形ABCD中放入六个长、宽都相同的小长方形,所标尺寸如图所示,求小长方形的宽AE.若AE=x(cm),依题意可得方程( )
A.6+2x=14﹣3x B.6+2x=x+(14﹣3x)
C.14﹣3x=6 D.6+2x=14﹣x
【解答】解:设AE为xcm,则AM为(14﹣3x)cm,
根据题意得出:∵AN=MW,∴AN+6=x+MR,
即6+2x=x+(14﹣3x)
故选:B.
3.一梯形面积为84cm2,高为8cm,它的下底比上底的2倍少3cm,求这个梯形的上底和下底的长度.解题时设梯形的上底为xcm,那么下面正确的方程是( )
A.8[x+(2x+3)]=84 B.8[x+(2x﹣3)]=84
C.×8[x+(2x+3)]=84 D.×8×[x+(2x﹣3)]=84
【解答】解:设梯形的上底为xcm,则下底为:(2x﹣3)cm,根据题意得出:
(x+2x﹣3)×8=84.
故选:D.
4.甲、乙两个油桶中装有体积相等的油.先把甲桶的油倒一半到乙桶(乙桶没有溢出),再把乙桶的油倒出给甲桶(甲桶没有溢出),这时两个油桶中的油的是( )
A.甲桶的油多
B.乙桶的油多
C.甲桶与乙桶一样多
D.无法判断,与原有的油的体积大小有关
【解答】解:设甲、乙两个油桶中油的重量为a.根据题意,得:
因为先把甲桶的油倒一半至乙桶,
甲桶的油=(1﹣)a,乙桶的油=(1+)a,
再把乙桶的油倒出三分之一给甲桶,
所以甲桶有油(1﹣)a+(1+)a×=a,
乙桶有油(1+) a (1﹣)=a,
所以甲乙两桶油一样多.
故选:C.
5.要锻造直径为2厘米,高为16厘米的圆柱形机器零件10件,则需直径为4厘米的圆钢柱长( )
A.10厘米 B.20厘米 C.30厘米 D.40厘米
【解答】解:设应截取直径4厘米的圆钢x厘米,
由题意得:π×()2×16×10=π×()2 x
解得:x=40.
故选:D.
6.六张形状大小完全相同的小长方形(白色部分)如图摆放在大长方形ABCD中,BC=n,AB=m,则图中两块阴影部分长方形的周长和是( )
A.4m B.4n C.2(m+n) D.4(m﹣n)
【解答】解:如图
由题意:EF=BM,HK=GD.
∴两个阴影部分长方形的四个长的和为AG+HK+CM+EF=AG+GD+BM+CM=AD+BC=2n.
设小白长方形的长为x,宽为y,则AE=GF=m﹣3y,CK=HM=m﹣x.
∴两个阴影部分长方形的四个宽的和为2AE+2CK=2(m﹣3y)+2(m﹣x)=4m﹣2(x+3y).
∵BM=x,CM=3y.
∴x+3y=BM+CM=BC=n.
∴两个阴影部分长方形的四个宽的和为4m﹣2n.
∴两块阴影部分长方形的周长和是2n+4m﹣2n=4m.
故选:A.
二.填空题(共6小题)
7.一个长方体水箱,从里面量长、宽、高分别为40cm、30cm和30cm,箱中水面高10cm,放进一个棱长为20cm的正方体铁块后,这时水面高为 15 cm.
【解答】解:设放入正方体铁块后水面高为h厘米,由题意得:
40×30×10+20×20×h=40×30×h,
解得:h=15.
答:这时水面高15厘米.
故答案为:15.
8.如图,一块长4厘米、宽1厘米的长方形纸板①,一块长5厘米、宽2厘米的长方形纸板②与一块正方形纸板③以及另两块长方形纸板④和⑤,恰好拼成一个大正方形,则大正方形的面积是 36 平方厘米.
【解答】解:设小正方形的边长为x,依题意得
1+x+2=4+5﹣x,
解得x=3,
∴大正方形的边长为6厘米,
∴大正方形的面积是6×6=36(平方厘米),
答:大正方形的面积是36平方厘米.
故答案是:36.
9.李红用40cm长的铁丝围成一个长方形,要使长方形的长比宽多4cm.设宽为xcm,则可列方程为 2(x+4+x)=40 ,围成的长方形的面积为 96cm2 .
【解答】解:设这个长方形的宽为xcm,则长为(x+4)cm,
则可列方程:2(x+4+x)=40,
解得:x=8,
围成的长方形的面积为8×12=96(cm2),
故答案为:2(x+4+x)=40,96cm2.
10.有一艘轮船的载重量是800吨,容积是795立方米.现要装运生铁和棉花两种物资,生铁每吨的体积为0.3立方米,棉花每吨的体积为4立方米,则生铁装 650 吨、棉花装 150 吨才能充分利用船的载重量和容积.
【解答】解:设生铁运x吨,则棉花运(800﹣x)吨,
由题意得出:0.3x+4(800﹣x)=795,
解得:x=650,
800﹣650=150(吨),
答:生铁运650吨,棉花运150吨,
故答案为:650;150.
11.现有含盐30%的盐水60千克,要把它变成浓度为40%的盐水,有下列两种方案:
(1)加盐,问需盐多少千克?若设需加盐x千克,所列方程为 60(1﹣10%)=(60+x)(1﹣40%) ,求得x= 30 .
(2)蒸发水,问需蒸发多少千克?若设需蒸发y千克,所列方程为 60×30%=(60﹣y)×40% ,求得y= 15 .
【解答】解:(1)设需要加盐x千克,
由题意得:60(1﹣10%)=(60+x)(1﹣40%).
解得 x=30
故答案是:60(1﹣10%)=(60+x)(1﹣40%);30;
(2)设需蒸发y千克,
由题意得:60×30%=(60﹣y)×40%
解得y=15.
故答案是:60×30%=(60﹣y)×40%;15.
12.实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在容器的5cm高度处连通(即管子底离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升cm.
(1)开始注水1分钟,丙的水位上升 cm.
(2)开始注入 或 分钟的水量后,乙的水位比甲高0.5cm.
【解答】解:(1)∵甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,
∵注水1分钟,乙的水位上升cm,
∴得到注水1分钟,丙的水位上升cm×4=cm;
(2)设开始注入t分钟的水量后,乙的水位比甲高0.5cm,有两种情况:
①甲的水位不变时;
由题意得,t﹣1=0.5,
解得:t=,
∵×=6>5,
∴此时丙容器已向乙容器溢水,
∵5÷=分钟,×=,即经过分钟时丙容器的水到达管子底部,乙的水位上升,
∴+2×(t﹣)﹣1=0.5,解得:t=;
②当乙的水位到达管子底部,甲的水位上升时,
∵乙的水位到达管子底部的时间为;+(5﹣)÷÷2=分钟,
∴5﹣1﹣2×(t﹣)=0.5,
解得:t=,
综上所述开始注入或分钟的水量后,乙的水位比甲高0.5cm.
故答案为cm;或.
三.解答题(共8小题)
13.在一个底面直径为5cm,高为16cm圆柱形瓶内装满水,再将瓶内的水倒入一个底面直径为6cm,高为10cm的圆柱形玻璃杯中,能否完全装下?若装不下,求瓶内水面还有多高?若未能装满,求玻璃杯内水面离杯口的距离?
【解答】解:设将瓶内的水倒入一个底面直径是6cm,高是10cm的圆柱形玻璃杯中时,水面高为xcm,
根据题意得π ()2 x=π ()2×16,
解得x=,
∵>10,
∴不能完全装下.
﹣10=(cm),
16×=1.6(cm),
答:装不下,那么瓶内水面还有1.6cm.
14.我们知道在一定条件下,弹簧的伸长量跟所挂物体质量成正比,根据图中给出的信息,解答下列问题:
(1)挂一个小砝码弹簧伸长 1 cm,挂一个大砝码弹簧伸长 2 cm.
(2)如果要使弹簧长度为10cm,应挂大砝码、小砝码各多少个?
【解答】解:(1)由图可知:挂一个小砝码弹簧伸长(6﹣3)÷3=1(cm),
挂一个大砝码弹簧伸长(7﹣3)÷2=2(cm),
故答案为:1,2;
(2)设应挂大砝码x个,则小砝码(5﹣x)个,
根据题意得:2x+(5﹣x)×1=10﹣3,
解得:x=2,
∴5﹣x=5﹣2=3,
答:应挂大砝码2个,小砝码3个.
15.如图,小明将一个正方形纸片剪去一个宽为5厘米的长条后,再从剩下的长方形纸片上剪去一个宽6厘米的长条,如果两次剪下的长条面积正好相等,那么每一个长条的面积为多少?
【解答】解:设原来正方形纸的边长是xcm,则第一次剪下的长条的长是xcm,宽是5cm,第二次剪下的长条的长是(x﹣5)cm,宽是6cm,
由题意得:5x=6(x﹣5),
解得:x=30,
则30×5=150(cm2).
答:每一个长条的面积为150cm2.
16.如图,小奥将一个正方形纸片剪去一个宽为4cm的长方形(记作A)后,再将剩下的长方形纸片剪去一个宽为5cm的长方形(记作B).
(1)若A与B的面积相等,求这个正方形的边长;
(2)若A的周长是B的周长的倍,求这个正方形的边长.
【解答】解:(1)设正方形的边长为xcm,
由题意,得4x=5(x﹣4).
解得x=20.
答:这个正方形的边长为20cm;
(2)设这个正方形的边长为ycm,
由题意,得6(2y+8)=7×2[5+(y﹣4)].
解得y=17.
答:这个正方形的边长为17cm.
17.一个长方形养鸡场的长边靠墙,墙长14米,其他三边用竹篱笆围成,现有长为35米的篱笆,爸爸的设计方案是长比宽多5米;妈妈的设计方案是长比宽多2米,你认为谁的设计合理,为什么?如果按这种设计,养鸡场的面积是多少?
【解答】解:设爸爸的设计方案中鸡场的宽为xm,则长为(x+5)m,
根据题意得:2x+(x+5)=35,
解得:x=10,
x+5=15m>14m,所以不符合实际;
设妈妈的设计方案中鸡场的宽为ym,则长为(y+2)m,
根据题意得:2y+(y+2)=35,
解得:y=11,
y+2=13m<14m,所以符合实际,
此时鸡场的面积为11×13=143m2,
答:妈妈的设计符合实际,鸡场的面积为143m2.
18.如图,是一块在电脑屏幕上出现的矩形色块图,由6个颜色不同的正方形组成,设中间最小的一个正方形边长为1,求这个矩形色块图的面积.
【解答】解:如图所示
DF﹣AE=1,AE=BE+1,2CF﹣DF=1
DF=AE+1,AE=CF+1+1,DF=CF+3,
2CF﹣CF﹣3=1,解得CF=4,
∴BE=5,AE=6,∴AB=11,BC=13
S=AB BC=11×13=143.
19.张师傅想用篱笆围一个长方形鸡舍,一边利用房屋外的一面墙(墙的长度为12米),其他三边用篱笆,且中间用篱笆隔开,并在如图位置开两扇宽各1米的门(门不用篱笆),若鸡舍的宽为(a+2)米,长比宽的还多1米.
(1)求所用篱笆的总长度是多少米?(用含a的代数式表示,且结果要化简)
(2)当所围成的鸡舍用去篱笆的总长度为21米时,求a的值;
(3)能用27.6米长的篱笆围成符合条件的鸡舍吗?若能围成,求出此时的a值;若不能围成,请说明理由.
【解答】解:(1)∵鸡舍的宽为(a+2)米,长比宽的还多1米,
∴鸡舍的长为(a+2)+1米,
∵两扇小门宽各2米,
∴篱笆的总长度L=3×鸡舍的宽度+鸡舍的长度﹣2×小门的宽度=3(a+2)+[(a+2)+1]﹣2×1=;
(2)将L=21代入L=得:=21,解得:a=2;
(3)将L=27.6代入L=得:=27.6,
解得:a=3.2,
当a=3.2时,鸡舍的宽度为(3.2+2)+1=14>12,
故27.6米的篱笆不能围成符合题意的鸡舍.
20.如图,A、B两点在数轴上对应的数分别为﹣20、40,在A、B两点处各放一个挡板,M、N两个电子小球同时从原点出发,M以2个单位/秒的速度向数轴负方向运动,N以4个单位/秒的速度向数轴正方向运动,碰到挡板后则反方向运动,速度大小不变,当两小球第一次相遇时都停止运动.设两个小球运动的时间为t,那么:
(1)当0<t<10时,M在数轴上对应的数可以表示为 ﹣2t ;
(2)小杨同学发现:当0<t<10时,2MB﹣NA始终为定值.小杨的发现是否正确?若正确,请求出这个定值;若不正确,请说明理由.
(3)在整个运动过程中,t为何值时M、N两个小球间的距离为6?请直接写出答案.
【解答】解:(1)M、N碰到挡板所需时间均为10s,
∴0<t<10时M未碰到挡板运动距离为2t,又M向负轴运动,则M对应数轴上的数为﹣2t,
故答案为﹣2t.
(2)0<t<10时,设O点在数轴上对应的数为0,
则MB=MO+OB=2t+40;NA=NO+OA=4t+20,
2MB﹣NA=2(2t+40)﹣(4t+20)=60,
故2MB﹣NA为定值,定值为60.
(3)0<t<10时,MN=MO+ON=2t+4t=6t,令MN=6则t=l;
10<t<20时,MN=MO+ON=AO﹣AM+BO﹣BN=20﹣(2t﹣20)+40﹣(4t﹣40)=120﹣6t;
令MN=6则t=19.
故t=1s或19s时,MN两个小球间距离为6.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2022/3/23 14:02:32;用户:杨晓忆;邮箱:syx071@;学号:24369258
第1页(共14页)
