2021--2022学年人教版七年级数学下册 第六章 实数 复习课件(共45张)
文档属性
| 名称 | 2021--2022学年人教版七年级数学下册 第六章 实数 复习课件(共45张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-03 12:46:09 | ||
图片预览









文档简介
(共45张PPT)
实数 复习
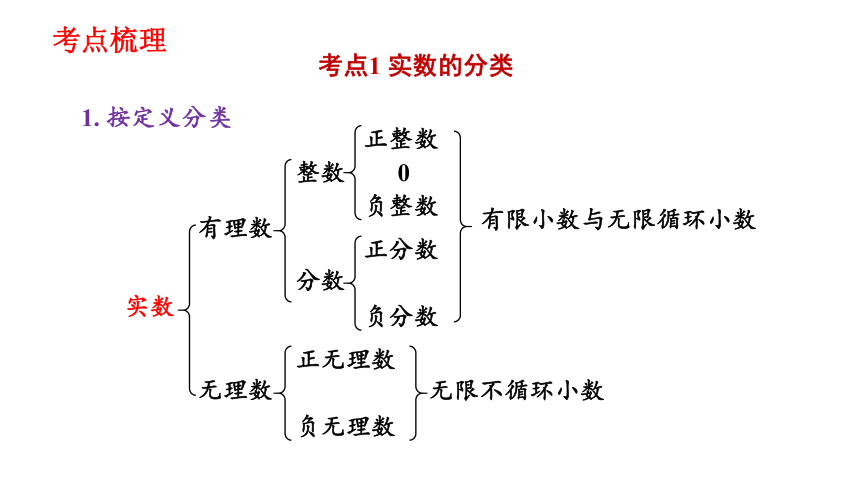
考点1 实数的分类
1. 按定义分类
实数
有理数
无理数
整数
分数
正整数
0
负整数
正分数
负分数
正无理数
负无理数
有限小数与无限循环小数
无限不循环小数
考点梳理
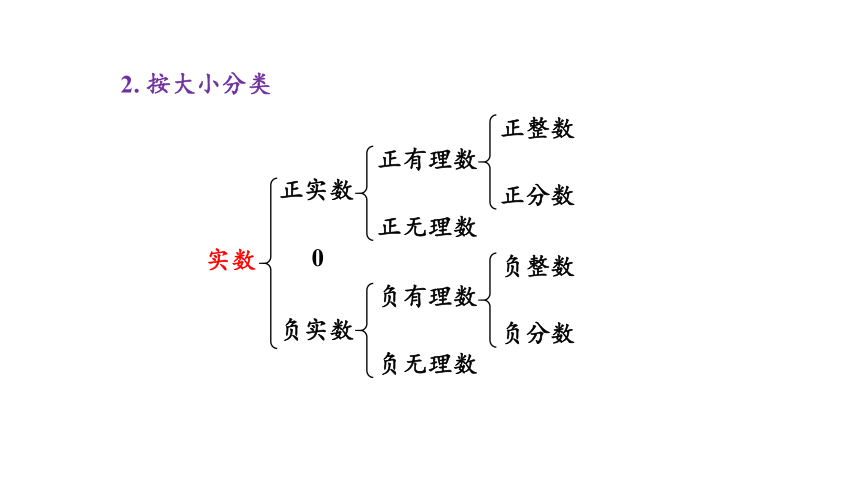
2. 按大小分类
实数
正实数
负实数
0
正有理数
正无理数
负有理数
负无理数
正整数
正分数
负整数
负分数
温馨提示
常见的无理数类型
(1)π及化简后含π的数,如 , π-1等.
(2)开方开不尽的数,如, 等.
(3)含有根号的三角函数值,如tan30°, sin60°等.
(4)有规律的无限不循环小数,如0.3030030003…(相邻两个3之间依次多一个0).
1.下列实数是无理数的是( )
A.-2 B. C. D.
D
考点专练
2.小幸学习了在数轴上画出表示无理数的点的方法后,进行以下练习:首先画出数轴,原点为O,在数轴上找到表示数2的点A,然后过点A作AB⊥OA,使AB=3.以点O为圆心,OB为半径作弧,交数轴正半轴于点P,则点P所表示的数介于( )
A.3和3.5之间 B.3.5和4之间
C.4和4.5之间 D.4.5和5之间
B
3.若盈余2万元记作+2万元,则-2万元表示( )
A.盈余2万元 B.亏损2万元
C.亏损-2万元 D.不盈余也不亏损
B
4.《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是:今有两数若其意义相反,则分别叫做正数与负数.若气温为零上10 ℃记作+10 ℃,则-3 ℃表示气温为( )
A.零上3 ℃ B.零下3 ℃
C.零上7 ℃ D.零下7 ℃
B
考点2 数轴
概念 规定了_______、_________和___________的直线叫做数轴 性质 ①实数与数轴上的点是___________的; ②离原点越远的数的绝对值越_____; ③数轴上右边的数总比左边的数_____. 用途 (1)利用数轴可以表示实数;
(2)利用数轴可以比较有理数的大小.
注意:一一对应是指每一个实数都能在数轴上找到一个点和它对应,数轴上的每个点,都有一个实数和它对应. 原点
正方向
单位长度
一一对应
大
大
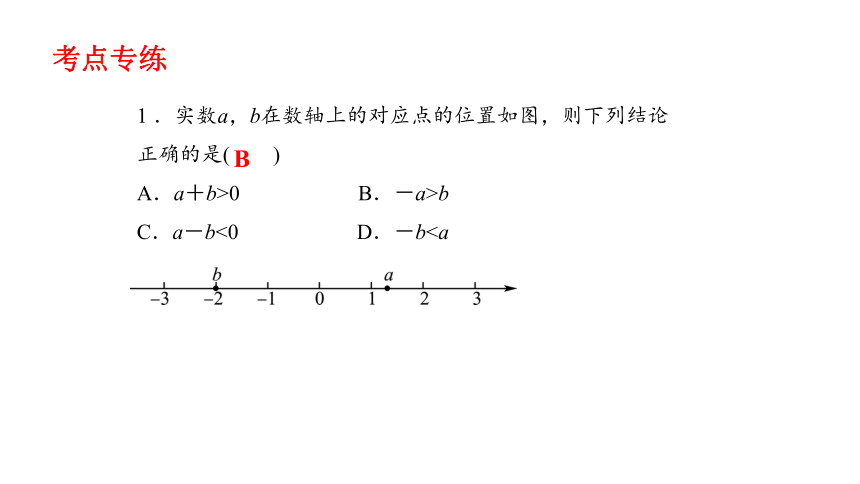
1 .实数a,b在数轴上的对应点的位置如图,则下列结论正确的是( )
A.a+b>0 B.-a>b
C.a-b<0 D.-b考点专练
B
2.在数轴上,点A表示-2.若从点A出发,沿数轴的正方向移动4个单位长度到达点B,则点B表示的数是( )
A.-6 B.-4 C.2 D.4
考点专练
C
2
1
0
-1
-2
3
4
5
-3
A
B
考点3 相反数、绝对值、倒数
此考点为必考内容,注意相反数、倒数、绝对值之间的区别.
概念 性质
相反数 只有_______不同的两个数互为相反数 1.0的相反数还是0
2.a,b互为相反数 a+b=0
3.在数轴上,表示互为相反数的两个点位于原点两侧(0除外),且与原点的距离_______
绝对值 一般地,数轴上表示数a的点与原点的_______叫做数a的绝对值,记作|a| 1.互为相反数的两个数的绝对值_______
倒 数 乘积是____的两个数互为倒数 1.a·b=1 a,b互为倒数
2.1和-1的倒数还是它本身
3.0没有倒数
注意:互为相反数的两个数关于原点对称,非正数(0或负数)的相反数是非负数(0或正数),相反数等于本身的数只有0 符号
相等
距离
相等
1
1.|-3|的值是( )
A.-3 B.3 C.- D.
考点专练
B
2.-5的倒数是( )
A.-5 B.5 C. D.-
D
3. 2的绝对值的倒数是( )
A.-2 B. C.2 D.±2
B
4.如图,数轴上有三个点A,B,C,若点A,B表示的数互为相反数,则图中点C对应的数是( )
A.-2 B.0 C.1 D.4
5.如图,数轴上点A所表示的数的倒数为( )
A.-3 B.3 C.- D.
C
C
考点4 平方根、算术平方根、立方根
平方根与算术平方根既是必考点又是易错点.
名称 a>0 a=0 a<0 定义与性质
平方根 ± 0 没有 0只有一个平方根,是0;
负数没有平方根.
平方根等于本身的数是0.
算术 平方根 0 没有 正数的算术平方根是一个正数;
0的算术平方根是0;
负数没有算术平方根.
算术平方根等于本身的数是0和1.
立方根 0 正数的立方根是正数;
0的立方根是0;
负数的立方根是负数.
任何数都有唯一的立方根与它对应,=-.
平方与开平方是互逆运算,一个正数有两个平方根,这两个平方根互为相反数,千万不能丢掉负的平方根.在实数范围内,每个数(包括正数、0、负数)均有一个立方根.
易错提示
1. 的算术平方根是( )
A.±9 B.±3 C.9 D.3
2. 的立方根为______.
考点专练
D
2
3. 的平方根是( )
A.4 B.±2 C.2 D.±4
B
4.-27的立方根是( )
A.3 B.-3 C.±3 D.-3
5.若实数m,n满足(m+1)2+ =0,则=____.
考点专练
2
D
考点5 近似数与科学计数法
近似数 与实际完全符合的数称为_________,与实际接近的数称为_________
精确度 一个近似数的最后一位是哪一位,就说这个近似数精确到哪一位
科学 记数法 1.把一个大于10的数表示成a×10n的形式(其中a大于或等于1且小于10,n是正整数)
2.科学记数法可以记大数也可以记小数,注意n的正负性.另外负数的科学记数法不要忘记负号
准确数
近似数
1.国务院第七次全国人口普查领导小组办公室5月11日发布,江西人口数约为45100000人,将45100000用科学记数法表示为_______________________.
考点专练
4.51×107
2.纳米技术,是研究结构尺寸在1至100纳米范围内材料的性质和应用.有一种纳米材料其理论厚度是0.00000000069 m,这个数用科学记数法表示正确的是( )
A.0.69×10-10 B.0.69×10-9
C.6.9×10-9 D.6.9×10-10
3.2021年5月11日,第七次全国人口普查数据显示,全国人口比第六次全国人口普查数据增加了7 206万人.7 206万用科学记数法表示为________________.
D
7.206×107
考点6 实数的大小比较
数轴比较法 在数轴上,右边的点表示的数总比左边的点表示的数_____
法则比较法 正数_____0,负数_____0,正数____一切负数;两个负数比较大小,绝对值大的反而小
作差比较法 1.若a-b>0,则a_____b
2.若a-b=0,则a_____b
3.若a-b<0,则a_____b
作商比较法 1.若a>0,b>0,则>1 a>b;=1 a=b;<1 a2.若a<0,b<0,则>1 ab
大
>
<
>
>
=
<
1.下列各数:-4,-2.8,0,|-4|,其中比-3小的数是( )
A.-4 B.|-4| C.0 D.-2.8
考点专练
A
2.下表是几种液体在标准大气压下的沸点:
液体名称 液态氧 液态氢 液态氮 液态氦
沸点/℃ -183 -253 -196 -268.9
则沸点最高的液体是( )
A.液态氧 B.液态氢 C.液态氮 D.液态氦
A
考点7 实数的运算
加法运算 同号两数相加,取与加数_________符号,并把_____________;
异号两数相加,绝对值相等时和为0;绝对值不相等时,取
_________较大的数的符号,并用较大的绝对值_______较小的绝对值;互为相反数的两数相加得____;一个数同0相加,仍得这个数.
口诀:同号相加大加小,符号跟着它俩人跑;异号相加大减小,符号跟着大的跑
减法运算 减去一个数,等于加上这个数的相反数,a-b=a+_______
相同的
绝对值相加
绝对值
减去
0
(-b)
乘法运算 两数相乘,同号得正,异号得负,绝对值相乘,任何数与0相乘,积仍为0. a·b=ab;(-a)·(-b)=_____;a·(-b)=-ab;0·a=____
除法运算 两个有理数相除,同号得正,异号得负,并把绝对值相除,0除以任何非0的数都得0,0不能作除数,除以一个不为0的数,等于乘这个数的倒数.a÷b=a· (b≠0);0÷b=0(b≠0)
ab
0
混合运算 的顺序 1.先算乘方、开方,再算乘除,最后算加减,如果有括号,要先算括号里面的,注意一定先计算各小项的值
2.没有括号,在同一级运算中,要按从左至右的顺序依次运算
1
有理数的 运算律 1.加法的交换律:a+b=b+a
2.加法的结合律:(a+b)+c=a+(b+c)
3.乘法的交换律:ab=ba
4.乘法的结合律:(ab)c=a(bc)
5.乘法对加法的分配律:a(b+c)=ab+ac
注意:实数的运算是中考的必考内容,经常把零指数幂、负整数指数幂、绝对值、二次根式、三角函数等知识结合起来考查,解决该类问题首先从各运算的含义出发,确定每项的符号、数值,再按运算顺序进行计算,灵活运用运算法则,细心计算. 1.计算:|-|+(-)2-(+)2.
解:原式= +(-++)(---)
=+2 ×(-1)
=-.
典例讲析
题型一 科学记数法
例1.2021年5月15日,我国“天问一号”探测器在火星成功着陆.火星具有和地球相近的环境,与地球最近时候的距离约55 000 000 km.将数字55 000 000用科学记数法表示为( )
A.0.55×108 B.5.5×107
C.5.5×106 D.55×106
B
例2我国天问一号火星探测器于2021年5月15日成功着陆火星表面.经测算,地球跟火星最远距离约400 000 000千米,其中数据400 000 000用科学记数法表示为( )
A.4×109 B.40×107
C.4×108 D.0.4×109
C
1.当|原数|≥10时,n为正整数,且等于原数的整数位数减1.
2.当0<原数<1时,n是负整数,且绝对值等于原数左起第一个非零数字前面0的个数(含小数点前面的那个0).
方法总结
1. 经过4.6亿千米的飞行,我国首次火星探测任务“天问一号”探测器于2021年5月15日在火星表面成功着陆,火星上首次留下了中国的印迹.将4.6亿用科学记数法表示为( )
A.4.6×109 B.0.46×109
C.46×108 D.4.6×108
跟踪练习
D
2.(2021·荆门)“绿水青山就是金山银山”某地积极响应党中央号召,大力推进农村厕所革命,已经累计投资1.012×108元资金.数据1.012×108可表示为( )
A.10.12亿 B.1.012亿
C.101.2亿 D.1 012亿
B
题型二 实数的大小比较
例3 实数2,0,-3, 中,最小的数是( )
A.2 B.0 C.-3 D.
例4 下列各数中,比3大比4小的无理数是( )
A.3.14 B. C. D.
C
C
⑥作差法;
⑦放缩法;
⑧取倒数法;
⑨作商法等.
方法总结
①数轴法;
②绝对值法;
③统一分子法;
④统一分母法;
⑤分子(母)有理化法;
实数大小比较方法
3.实数a,b,c在数轴上的对应点的位置如图,下列关系式一定成立的是( )
A. > B.a+c>b+c
C.2a>2b D.a-c>b-c
A
跟踪练习
例4 |1-|=( )
A.1- B.-1 C.1+ D.-1-
B
题型三 实数的运算
(1)在实数运算中,要注意括号、正负号、运算顺序、公式、运算律的正确使用,以提高运算的准确性.
(2)三个常见非负数:①实数的绝对值是非负数,即≥0;②平方数是非负数,即a2≥0;③算术平方根是非负数,即≥0.
(3)注意在理解的基础上熟练运用整数指数幂和特殊角的三角函数值.
方法总结
题型四 生活中的数学
问题情境1
1.如果零上15 ℃记作+15 ℃,那么零下3 ℃可记作( )
A.-3 ℃ B.+3 ℃
C.-12 ℃ D.12 ℃
A
2.北京某天的最高气温为3 ℃,最低气温为-3 ℃,则这一天的最高气温与最低气温的差为( )
A.6 ℃ B.8 ℃
C.10 ℃ D.-10 ℃
A
3.据光明日报网,中国科学技术大学的潘建伟、陆朝阳等人构建了一台76个光子100个模式的量子计算机“九章”.它处理“高斯玻色取样”的速度比目前最快的超级计算机“富岳”快一百万亿倍.也就是说,超级计算机需要一亿年完成的任务,“九章”只需一分钟.其中一百万亿用科学记数法表示为( )
A.10×1012 B.10×1014
C.1×1014 D.1×1015
问题情境2
C
4.中芯国际集成电路制造有限公司,是世界领先的集成电路晶圆代工企业之一,也是中国内地技术最先进、配套最完善、规模最大、跨国经营的集成电路制造企业集团,中芯国际第一代14纳米FinFET技术取得了突破性进展,并于2019年第四季度进入量产,代表了中国大陆自主研发集成电路的最先进水平,14纳米=0.000 000 014米,0.000 000 014用科学记数法表示为( )
A.1.4×10-7 B.14×10-7
C.1.4×10-8 D.1.4×10-9
C
5.如果物体先向右运动5 m,再向右运动3 m,那么两次运动后,距离原地( )
A.2 m B.3 m C.8 m D.5 m
问题情境3
C
实数 复习
考点1 实数的分类
1. 按定义分类
实数
有理数
无理数
整数
分数
正整数
0
负整数
正分数
负分数
正无理数
负无理数
有限小数与无限循环小数
无限不循环小数
考点梳理
2. 按大小分类
实数
正实数
负实数
0
正有理数
正无理数
负有理数
负无理数
正整数
正分数
负整数
负分数
温馨提示
常见的无理数类型
(1)π及化简后含π的数,如 , π-1等.
(2)开方开不尽的数,如, 等.
(3)含有根号的三角函数值,如tan30°, sin60°等.
(4)有规律的无限不循环小数,如0.3030030003…(相邻两个3之间依次多一个0).
1.下列实数是无理数的是( )
A.-2 B. C. D.
D
考点专练
2.小幸学习了在数轴上画出表示无理数的点的方法后,进行以下练习:首先画出数轴,原点为O,在数轴上找到表示数2的点A,然后过点A作AB⊥OA,使AB=3.以点O为圆心,OB为半径作弧,交数轴正半轴于点P,则点P所表示的数介于( )
A.3和3.5之间 B.3.5和4之间
C.4和4.5之间 D.4.5和5之间
B
3.若盈余2万元记作+2万元,则-2万元表示( )
A.盈余2万元 B.亏损2万元
C.亏损-2万元 D.不盈余也不亏损
B
4.《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是:今有两数若其意义相反,则分别叫做正数与负数.若气温为零上10 ℃记作+10 ℃,则-3 ℃表示气温为( )
A.零上3 ℃ B.零下3 ℃
C.零上7 ℃ D.零下7 ℃
B
考点2 数轴
概念 规定了_______、_________和___________的直线叫做数轴 性质 ①实数与数轴上的点是___________的; ②离原点越远的数的绝对值越_____; ③数轴上右边的数总比左边的数_____. 用途 (1)利用数轴可以表示实数;
(2)利用数轴可以比较有理数的大小.
注意:一一对应是指每一个实数都能在数轴上找到一个点和它对应,数轴上的每个点,都有一个实数和它对应. 原点
正方向
单位长度
一一对应
大
大
1 .实数a,b在数轴上的对应点的位置如图,则下列结论正确的是( )
A.a+b>0 B.-a>b
C.a-b<0 D.-b
B
2.在数轴上,点A表示-2.若从点A出发,沿数轴的正方向移动4个单位长度到达点B,则点B表示的数是( )
A.-6 B.-4 C.2 D.4
考点专练
C
2
1
0
-1
-2
3
4
5
-3
A
B
考点3 相反数、绝对值、倒数
此考点为必考内容,注意相反数、倒数、绝对值之间的区别.
概念 性质
相反数 只有_______不同的两个数互为相反数 1.0的相反数还是0
2.a,b互为相反数 a+b=0
3.在数轴上,表示互为相反数的两个点位于原点两侧(0除外),且与原点的距离_______
绝对值 一般地,数轴上表示数a的点与原点的_______叫做数a的绝对值,记作|a| 1.互为相反数的两个数的绝对值_______
倒 数 乘积是____的两个数互为倒数 1.a·b=1 a,b互为倒数
2.1和-1的倒数还是它本身
3.0没有倒数
注意:互为相反数的两个数关于原点对称,非正数(0或负数)的相反数是非负数(0或正数),相反数等于本身的数只有0 符号
相等
距离
相等
1
1.|-3|的值是( )
A.-3 B.3 C.- D.
考点专练
B
2.-5的倒数是( )
A.-5 B.5 C. D.-
D
3. 2的绝对值的倒数是( )
A.-2 B. C.2 D.±2
B
4.如图,数轴上有三个点A,B,C,若点A,B表示的数互为相反数,则图中点C对应的数是( )
A.-2 B.0 C.1 D.4
5.如图,数轴上点A所表示的数的倒数为( )
A.-3 B.3 C.- D.
C
C
考点4 平方根、算术平方根、立方根
平方根与算术平方根既是必考点又是易错点.
名称 a>0 a=0 a<0 定义与性质
平方根 ± 0 没有 0只有一个平方根,是0;
负数没有平方根.
平方根等于本身的数是0.
算术 平方根 0 没有 正数的算术平方根是一个正数;
0的算术平方根是0;
负数没有算术平方根.
算术平方根等于本身的数是0和1.
立方根 0 正数的立方根是正数;
0的立方根是0;
负数的立方根是负数.
任何数都有唯一的立方根与它对应,=-.
平方与开平方是互逆运算,一个正数有两个平方根,这两个平方根互为相反数,千万不能丢掉负的平方根.在实数范围内,每个数(包括正数、0、负数)均有一个立方根.
易错提示
1. 的算术平方根是( )
A.±9 B.±3 C.9 D.3
2. 的立方根为______.
考点专练
D
2
3. 的平方根是( )
A.4 B.±2 C.2 D.±4
B
4.-27的立方根是( )
A.3 B.-3 C.±3 D.-3
5.若实数m,n满足(m+1)2+ =0,则=____.
考点专练
2
D
考点5 近似数与科学计数法
近似数 与实际完全符合的数称为_________,与实际接近的数称为_________
精确度 一个近似数的最后一位是哪一位,就说这个近似数精确到哪一位
科学 记数法 1.把一个大于10的数表示成a×10n的形式(其中a大于或等于1且小于10,n是正整数)
2.科学记数法可以记大数也可以记小数,注意n的正负性.另外负数的科学记数法不要忘记负号
准确数
近似数
1.国务院第七次全国人口普查领导小组办公室5月11日发布,江西人口数约为45100000人,将45100000用科学记数法表示为_______________________.
考点专练
4.51×107
2.纳米技术,是研究结构尺寸在1至100纳米范围内材料的性质和应用.有一种纳米材料其理论厚度是0.00000000069 m,这个数用科学记数法表示正确的是( )
A.0.69×10-10 B.0.69×10-9
C.6.9×10-9 D.6.9×10-10
3.2021年5月11日,第七次全国人口普查数据显示,全国人口比第六次全国人口普查数据增加了7 206万人.7 206万用科学记数法表示为________________.
D
7.206×107
考点6 实数的大小比较
数轴比较法 在数轴上,右边的点表示的数总比左边的点表示的数_____
法则比较法 正数_____0,负数_____0,正数____一切负数;两个负数比较大小,绝对值大的反而小
作差比较法 1.若a-b>0,则a_____b
2.若a-b=0,则a_____b
3.若a-b<0,则a_____b
作商比较法 1.若a>0,b>0,则>1 a>b;=1 a=b;<1 a
大
>
<
>
>
=
<
1.下列各数:-4,-2.8,0,|-4|,其中比-3小的数是( )
A.-4 B.|-4| C.0 D.-2.8
考点专练
A
2.下表是几种液体在标准大气压下的沸点:
液体名称 液态氧 液态氢 液态氮 液态氦
沸点/℃ -183 -253 -196 -268.9
则沸点最高的液体是( )
A.液态氧 B.液态氢 C.液态氮 D.液态氦
A
考点7 实数的运算
加法运算 同号两数相加,取与加数_________符号,并把_____________;
异号两数相加,绝对值相等时和为0;绝对值不相等时,取
_________较大的数的符号,并用较大的绝对值_______较小的绝对值;互为相反数的两数相加得____;一个数同0相加,仍得这个数.
口诀:同号相加大加小,符号跟着它俩人跑;异号相加大减小,符号跟着大的跑
减法运算 减去一个数,等于加上这个数的相反数,a-b=a+_______
相同的
绝对值相加
绝对值
减去
0
(-b)
乘法运算 两数相乘,同号得正,异号得负,绝对值相乘,任何数与0相乘,积仍为0. a·b=ab;(-a)·(-b)=_____;a·(-b)=-ab;0·a=____
除法运算 两个有理数相除,同号得正,异号得负,并把绝对值相除,0除以任何非0的数都得0,0不能作除数,除以一个不为0的数,等于乘这个数的倒数.a÷b=a· (b≠0);0÷b=0(b≠0)
ab
0
混合运算 的顺序 1.先算乘方、开方,再算乘除,最后算加减,如果有括号,要先算括号里面的,注意一定先计算各小项的值
2.没有括号,在同一级运算中,要按从左至右的顺序依次运算
1
有理数的 运算律 1.加法的交换律:a+b=b+a
2.加法的结合律:(a+b)+c=a+(b+c)
3.乘法的交换律:ab=ba
4.乘法的结合律:(ab)c=a(bc)
5.乘法对加法的分配律:a(b+c)=ab+ac
注意:实数的运算是中考的必考内容,经常把零指数幂、负整数指数幂、绝对值、二次根式、三角函数等知识结合起来考查,解决该类问题首先从各运算的含义出发,确定每项的符号、数值,再按运算顺序进行计算,灵活运用运算法则,细心计算. 1.计算:|-|+(-)2-(+)2.
解:原式= +(-++)(---)
=+2 ×(-1)
=-.
典例讲析
题型一 科学记数法
例1.2021年5月15日,我国“天问一号”探测器在火星成功着陆.火星具有和地球相近的环境,与地球最近时候的距离约55 000 000 km.将数字55 000 000用科学记数法表示为( )
A.0.55×108 B.5.5×107
C.5.5×106 D.55×106
B
例2我国天问一号火星探测器于2021年5月15日成功着陆火星表面.经测算,地球跟火星最远距离约400 000 000千米,其中数据400 000 000用科学记数法表示为( )
A.4×109 B.40×107
C.4×108 D.0.4×109
C
1.当|原数|≥10时,n为正整数,且等于原数的整数位数减1.
2.当0<原数<1时,n是负整数,且绝对值等于原数左起第一个非零数字前面0的个数(含小数点前面的那个0).
方法总结
1. 经过4.6亿千米的飞行,我国首次火星探测任务“天问一号”探测器于2021年5月15日在火星表面成功着陆,火星上首次留下了中国的印迹.将4.6亿用科学记数法表示为( )
A.4.6×109 B.0.46×109
C.46×108 D.4.6×108
跟踪练习
D
2.(2021·荆门)“绿水青山就是金山银山”某地积极响应党中央号召,大力推进农村厕所革命,已经累计投资1.012×108元资金.数据1.012×108可表示为( )
A.10.12亿 B.1.012亿
C.101.2亿 D.1 012亿
B
题型二 实数的大小比较
例3 实数2,0,-3, 中,最小的数是( )
A.2 B.0 C.-3 D.
例4 下列各数中,比3大比4小的无理数是( )
A.3.14 B. C. D.
C
C
⑥作差法;
⑦放缩法;
⑧取倒数法;
⑨作商法等.
方法总结
①数轴法;
②绝对值法;
③统一分子法;
④统一分母法;
⑤分子(母)有理化法;
实数大小比较方法
3.实数a,b,c在数轴上的对应点的位置如图,下列关系式一定成立的是( )
A. > B.a+c>b+c
C.2a>2b D.a-c>b-c
A
跟踪练习
例4 |1-|=( )
A.1- B.-1 C.1+ D.-1-
B
题型三 实数的运算
(1)在实数运算中,要注意括号、正负号、运算顺序、公式、运算律的正确使用,以提高运算的准确性.
(2)三个常见非负数:①实数的绝对值是非负数,即≥0;②平方数是非负数,即a2≥0;③算术平方根是非负数,即≥0.
(3)注意在理解的基础上熟练运用整数指数幂和特殊角的三角函数值.
方法总结
题型四 生活中的数学
问题情境1
1.如果零上15 ℃记作+15 ℃,那么零下3 ℃可记作( )
A.-3 ℃ B.+3 ℃
C.-12 ℃ D.12 ℃
A
2.北京某天的最高气温为3 ℃,最低气温为-3 ℃,则这一天的最高气温与最低气温的差为( )
A.6 ℃ B.8 ℃
C.10 ℃ D.-10 ℃
A
3.据光明日报网,中国科学技术大学的潘建伟、陆朝阳等人构建了一台76个光子100个模式的量子计算机“九章”.它处理“高斯玻色取样”的速度比目前最快的超级计算机“富岳”快一百万亿倍.也就是说,超级计算机需要一亿年完成的任务,“九章”只需一分钟.其中一百万亿用科学记数法表示为( )
A.10×1012 B.10×1014
C.1×1014 D.1×1015
问题情境2
C
4.中芯国际集成电路制造有限公司,是世界领先的集成电路晶圆代工企业之一,也是中国内地技术最先进、配套最完善、规模最大、跨国经营的集成电路制造企业集团,中芯国际第一代14纳米FinFET技术取得了突破性进展,并于2019年第四季度进入量产,代表了中国大陆自主研发集成电路的最先进水平,14纳米=0.000 000 014米,0.000 000 014用科学记数法表示为( )
A.1.4×10-7 B.14×10-7
C.1.4×10-8 D.1.4×10-9
C
5.如果物体先向右运动5 m,再向右运动3 m,那么两次运动后,距离原地( )
A.2 m B.3 m C.8 m D.5 m
问题情境3
C
