北师大版七年级数学下册2.1.2 垂线 优质习题课件(共23张PPT)
文档属性
| 名称 | 北师大版七年级数学下册2.1.2 垂线 优质习题课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 989.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-03 13:50:52 | ||
图片预览




文档简介
(共23张PPT)
第二章 相交线与平行线
1 两条直线的位置关系
第二课时 垂 线
名 师 点 睛
知识点1 垂线及其画法
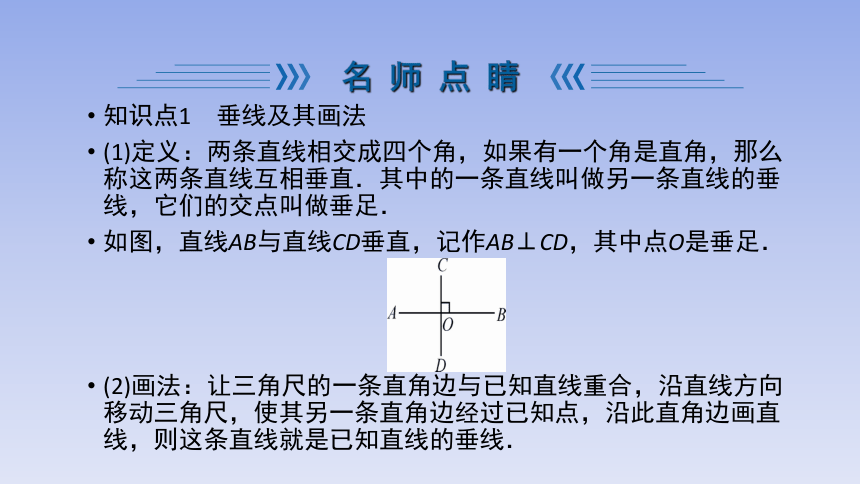
(1)定义:两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相垂直.其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
如图,直线AB与直线CD垂直,记作AB⊥CD,其中点O是垂足.
(2)画法:让三角尺的一条直角边与已知直线重合,沿直线方向移动三角尺,使其另一条直角边经过已知点,沿此直角边画直线,则这条直线就是已知直线的垂线.
知识点2 垂线的性质
(1)平面内,过一点有且只有一条直线与已知直线垂直.
(2)直线外一点与直线上各点连接的所有线段中,垂线段最短.
知识点3 点到直线的距离
直线外一点到这条直线的垂线段的长度叫做点到直线的距离.
【典例】以下关于距离的四种说法中,正确的有( )
①连接两点的线段叫做两点的距离;②连接直线外一点和直线上的点的线段叫做点到直线的距离;③从直线外一点,所引的这条直线的垂线叫做点到直线的距离;④直线外一点到这条直线的垂线段的长度叫做点到直线的距离.
A.1个 B.2个
C.3个 D.4个
分析:点到直线的距离是垂线段的长度,所以④正确,①②③错误,故选A.
答案:A
点评:“点到直线的距离”实质上是直线外一点到垂足之间的距离.
基 础 过 关
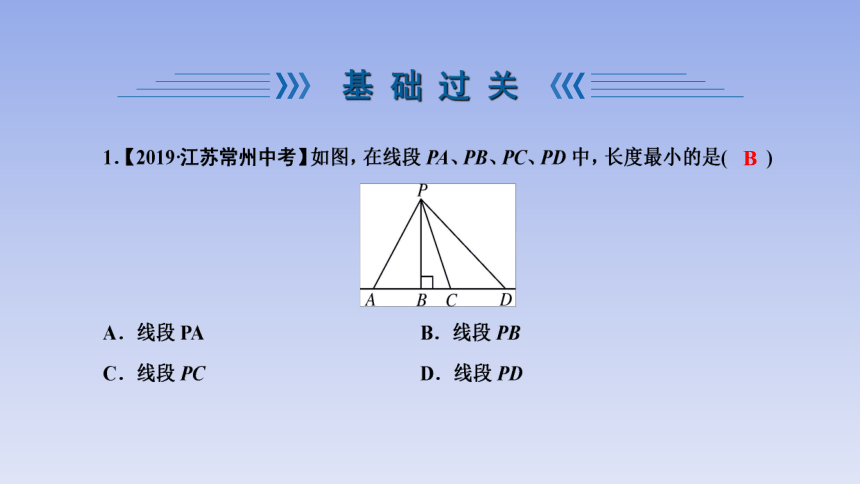
B
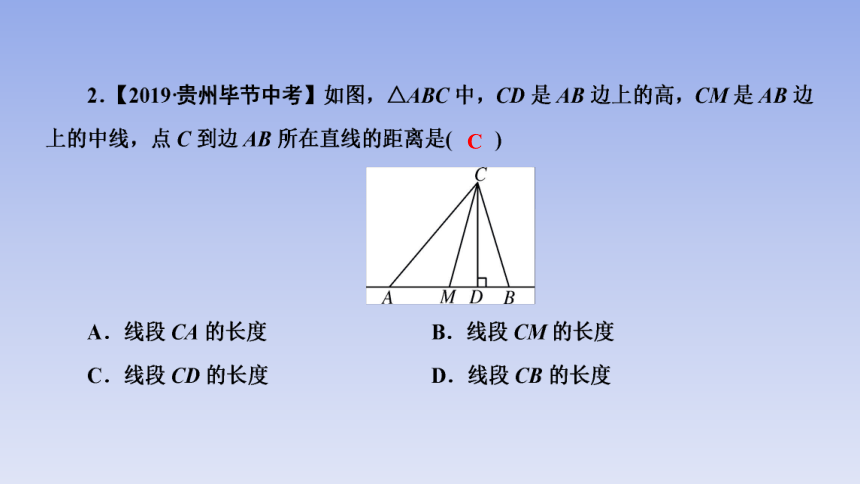
C
A
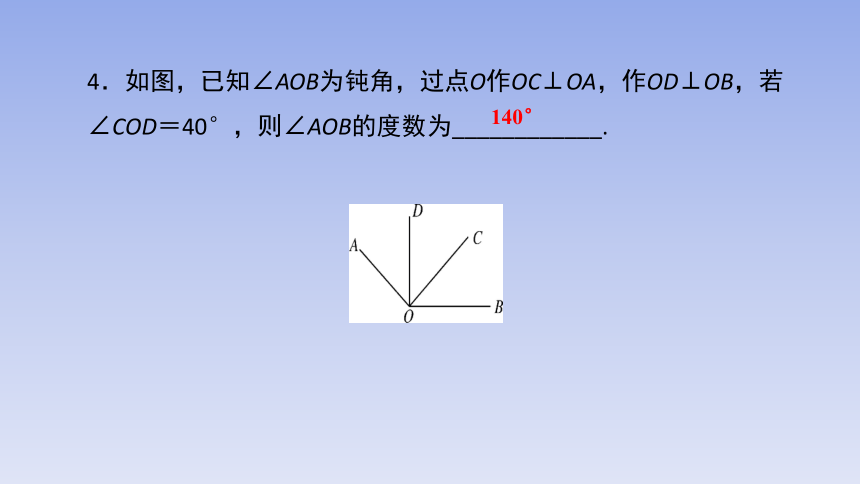
4.如图,已知∠AOB为钝角,过点O作OC⊥OA,作OD⊥OB,若∠COD=40°,则∠AOB的度数为____________.
140°
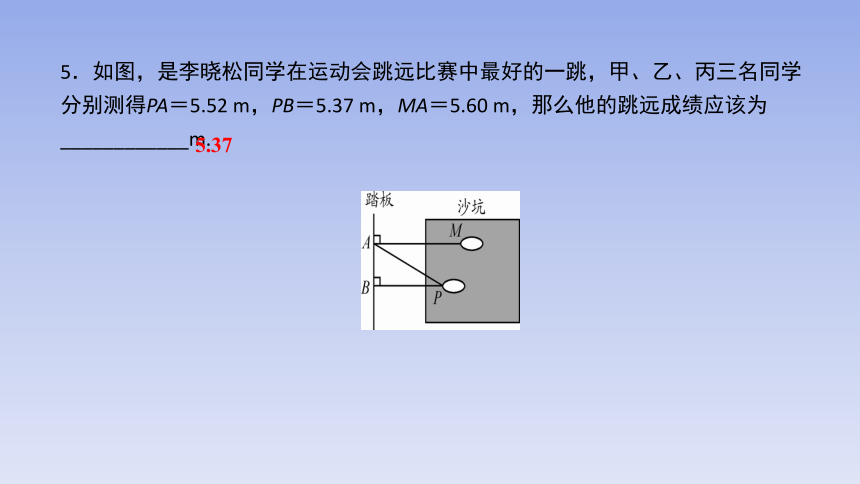
5.如图,是李晓松同学在运动会跳远比赛中最好的一跳,甲、乙、丙三名同学分别测得PA=5.52 m,PB=5.37 m,MA=5.60 m,那么他的跳远成绩应该为____________m.
5.37
6.如图,直线AB、CD相交于点O,OE⊥CD于点O,OD平分∠BOF,∠BOE=50°,求∠AOC、∠EOF和∠AOF的度数.
7.如图,一辆汽车在直线形公路AB上由A向B行驶,M、N是分别位于公路AB两侧的两所学校.
(1)汽车在公路上行驶时,会对两所学校教学都造成影响,当汽车行驶到何处时,分别对两所学校影响最大?请在图上标出来;
(2)当汽车从A向B行驶时,在哪一段上对两学校影响越来越大?在哪一段上对两学校影响越来越小?在哪一段上对M学校影响逐渐减小而对N学校影响逐渐增大?
能 力 提 升
8.已知△ABC中,BC=6,AC=3,CP⊥AB,垂足为点P,则CP的长可能是( )
A.2 B.4
C.5 D.7
A
C
B
11.如图,AB、CD、EF相交于点O,AB⊥CD,OG平分∠AOE,∠DOF=42°,则∠AOG的度数为( )
A.56°
B.59°
C.60°
D.66°
B
12.如图,AC⊥BC于点C,CD⊥AB于点D,DE⊥BC于点E,能表示点到直线(或线段)的距离的线段有____________条.
8
13.如图,已知AB⊥BD,BC⊥CD,AD=8,BC=6,则线段BD长的取值范围是____________.
614.如图,直线AB、CD相交于点O,OE⊥AB,∠DOF=90°,OB平分∠DOG.给出下列结论:①当∠AOF=60°时,∠DOE=60°;②OD为∠EOG的平分线;③与∠BOD相等的角有3个;④∠COG=∠AOB-2∠EOF.其中正确的结论有____________.(把所有正确结论的序号都填在横线上)
①③④
15.如图,在小河l的同侧有一个净化水厂A和村庄B,B村的生活用水要到小河l中去提,饮用净化水要到净化水厂A去取,B村的村民怎样走到河边最近?怎样走到净化水厂最近?请你画出图形并说明理由.
思 维 训 练
16.如图,点O为直线AB上一点,OC为一射线,OE平分∠AOC,OF平分∠BOC.
(1)若∠BOC=50°,试探究OE、OF的位置关系;
(2)若∠BOC为任意角α(0°<α<180°),(1)中OE、OF的位置关系是否仍成立?请说明理由.由此你发现什么规律?
第二章 相交线与平行线
1 两条直线的位置关系
第二课时 垂 线
名 师 点 睛
知识点1 垂线及其画法
(1)定义:两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相垂直.其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
如图,直线AB与直线CD垂直,记作AB⊥CD,其中点O是垂足.
(2)画法:让三角尺的一条直角边与已知直线重合,沿直线方向移动三角尺,使其另一条直角边经过已知点,沿此直角边画直线,则这条直线就是已知直线的垂线.
知识点2 垂线的性质
(1)平面内,过一点有且只有一条直线与已知直线垂直.
(2)直线外一点与直线上各点连接的所有线段中,垂线段最短.
知识点3 点到直线的距离
直线外一点到这条直线的垂线段的长度叫做点到直线的距离.
【典例】以下关于距离的四种说法中,正确的有( )
①连接两点的线段叫做两点的距离;②连接直线外一点和直线上的点的线段叫做点到直线的距离;③从直线外一点,所引的这条直线的垂线叫做点到直线的距离;④直线外一点到这条直线的垂线段的长度叫做点到直线的距离.
A.1个 B.2个
C.3个 D.4个
分析:点到直线的距离是垂线段的长度,所以④正确,①②③错误,故选A.
答案:A
点评:“点到直线的距离”实质上是直线外一点到垂足之间的距离.
基 础 过 关
B
C
A
4.如图,已知∠AOB为钝角,过点O作OC⊥OA,作OD⊥OB,若∠COD=40°,则∠AOB的度数为____________.
140°
5.如图,是李晓松同学在运动会跳远比赛中最好的一跳,甲、乙、丙三名同学分别测得PA=5.52 m,PB=5.37 m,MA=5.60 m,那么他的跳远成绩应该为____________m.
5.37
6.如图,直线AB、CD相交于点O,OE⊥CD于点O,OD平分∠BOF,∠BOE=50°,求∠AOC、∠EOF和∠AOF的度数.
7.如图,一辆汽车在直线形公路AB上由A向B行驶,M、N是分别位于公路AB两侧的两所学校.
(1)汽车在公路上行驶时,会对两所学校教学都造成影响,当汽车行驶到何处时,分别对两所学校影响最大?请在图上标出来;
(2)当汽车从A向B行驶时,在哪一段上对两学校影响越来越大?在哪一段上对两学校影响越来越小?在哪一段上对M学校影响逐渐减小而对N学校影响逐渐增大?
能 力 提 升
8.已知△ABC中,BC=6,AC=3,CP⊥AB,垂足为点P,则CP的长可能是( )
A.2 B.4
C.5 D.7
A
C
B
11.如图,AB、CD、EF相交于点O,AB⊥CD,OG平分∠AOE,∠DOF=42°,则∠AOG的度数为( )
A.56°
B.59°
C.60°
D.66°
B
12.如图,AC⊥BC于点C,CD⊥AB于点D,DE⊥BC于点E,能表示点到直线(或线段)的距离的线段有____________条.
8
13.如图,已知AB⊥BD,BC⊥CD,AD=8,BC=6,则线段BD长的取值范围是____________.
6
①③④
15.如图,在小河l的同侧有一个净化水厂A和村庄B,B村的生活用水要到小河l中去提,饮用净化水要到净化水厂A去取,B村的村民怎样走到河边最近?怎样走到净化水厂最近?请你画出图形并说明理由.
思 维 训 练
16.如图,点O为直线AB上一点,OC为一射线,OE平分∠AOC,OF平分∠BOC.
(1)若∠BOC=50°,试探究OE、OF的位置关系;
(2)若∠BOC为任意角α(0°<α<180°),(1)中OE、OF的位置关系是否仍成立?请说明理由.由此你发现什么规律?
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
