北师大版七年级数学下册2.1_第1课时 对顶角、补角与余角 课件(共16张PPT)
文档属性
| 名称 | 北师大版七年级数学下册2.1_第1课时 对顶角、补角与余角 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 945.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-03 13:52:56 | ||
图片预览




文档简介
(共16张PPT)
版本:北师大版
章节:七年级下册 第二章 第一节
2.1 两条直线的位置关系
第1课时 对顶角、补角与余角
1.通过观察生活模型,会描述平面内两条直线的位置关系;
2.会辨别两个角是否是对顶角、互为补角、互为余角,并利用其性质进行实际应用;
3.通过动手操作和小组合作,发展空间观念、推理能力和初步的几何语言表达能力.
学习目标
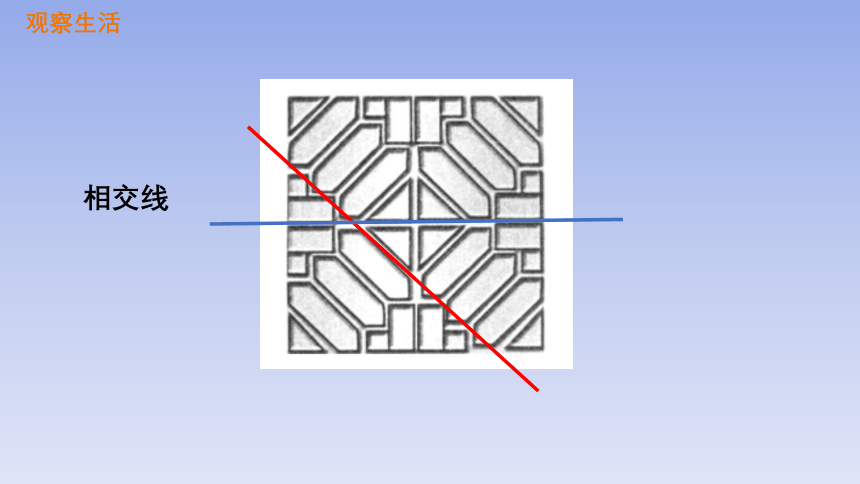
河南省社旗县清山会馆窗棂图案
l1
l2
相交
只有一个公共点
l3
l4
l5
平行
没有公共点
同一平面
观察生活
相交线
观察生活
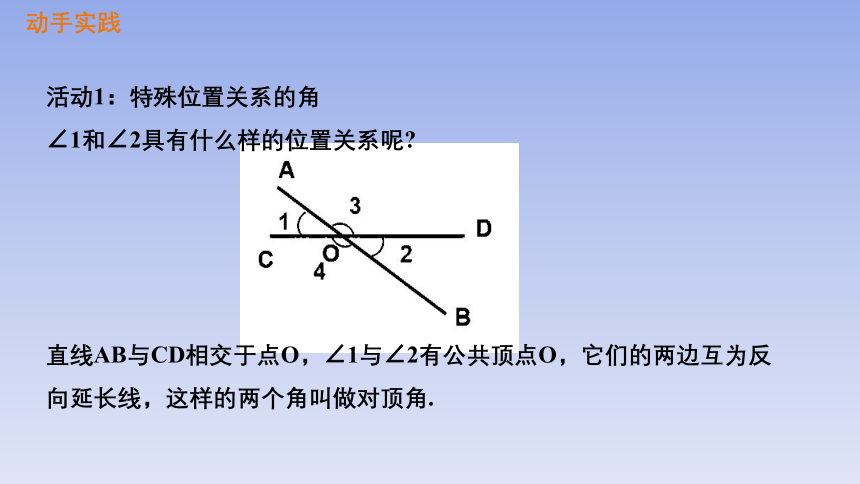
活动1:特殊位置关系的角
∠1和∠2具有什么样的位置关系呢
直线AB与CD相交于点O,∠1与∠2有公共顶点O,它们的两边互为反向延长线,这样的两个角叫做对顶角.
动手实践
下列各图中,∠1与∠2互为对顶角的是( )
C
判断两个角是否是对顶角的标准是什么?
动手实践
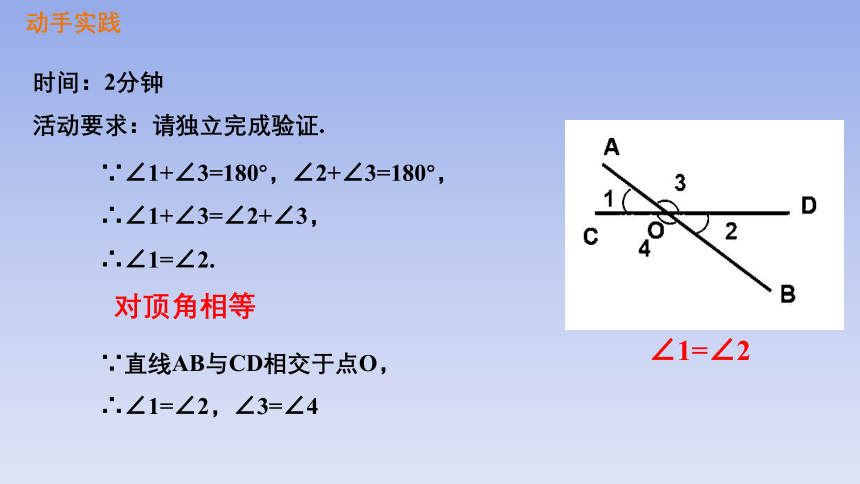
时间:2分钟
活动要求:请独立完成验证.
∵∠1+∠3=180°,∠2+∠3=180°,
∴∠1+∠3=∠2+∠3,
∴∠1=∠2.
∠1=∠2
∵直线AB与CD相交于点O,
∴∠1=∠2,∠3=∠4
对顶角相等
动手实践
活动2:特殊数量关系的角
如果两个角的和是180°,
那么称这两个角互为补角.
结论1:同角的补角相等.
∵∠1+∠3=180°, ∠2+∠3=180°
∴∠1=∠2
结论2:等角的补角相等.
∵∠1+∠3=180°,∠2+∠4=180°,
又∵∠1=∠2,∴∠3=∠4
动手实践
活动2:特殊数量关系的角
如果两个角的和是90°,那么称这两个角互为余角.
猜想:同角或等角的余角相等.
动手实践
动手实践
活动2:特殊数量关系的角
若∠ABE=∠BEF=∠ACF=∠CFE=90°,类比补角的性质来验证自己的猜想.
时间:5分钟
活动要求:小组合作,交流探讨,利用图中标出数字的角验证猜想,一人画图,一人写说理过程一人解说,一人拍照上传.
结论:同角或等角的余角相等.
小组合作
D
O
C
已知:ON与DC交于点O,∠ 1=∠2,∠DON=∠CON=90°.
问题1:有哪些角互为补角?有哪些角互为余角?
问题2:∠3与∠4有什么关系?为什么?
问题3:∠AOC与∠BOD有什么关系?为什么?
实践巩固
D
O
C
已知:ON与DC交于点O,∠ 1=∠2,∠DON=∠CON=90°.
问题1:有哪些角互为补角?有哪些角互为余角?
问题2:∠3与∠4有什么关系?为什么?
问题3:∠AOC与∠BOD有什么关系?为什么?
实践巩固
时间:3分钟
要求:完成平板推送题目. 对错误率较高的题目进行小组交流. 组内互助,总结反思.
当堂检测
通过本节课的探索与交流,你有哪些收获?
归纳小结
如图,将一个长方形纸片沿着直线EF折叠,点C落在点H处;再将∠D沿着EE折叠,使DE落在直线EH上:
问题1:∠FEG等于多少度?为什么?
问题2:上述折纸的图形中,还有哪些角互为余角?哪些角互为补角?
布置作业
版本:北师大版
章节:七年级下册 第二章 第一节
2.1 两条直线的位置关系
第1课时 对顶角、补角与余角
1.通过观察生活模型,会描述平面内两条直线的位置关系;
2.会辨别两个角是否是对顶角、互为补角、互为余角,并利用其性质进行实际应用;
3.通过动手操作和小组合作,发展空间观念、推理能力和初步的几何语言表达能力.
学习目标
河南省社旗县清山会馆窗棂图案
l1
l2
相交
只有一个公共点
l3
l4
l5
平行
没有公共点
同一平面
观察生活
相交线
观察生活
活动1:特殊位置关系的角
∠1和∠2具有什么样的位置关系呢
直线AB与CD相交于点O,∠1与∠2有公共顶点O,它们的两边互为反向延长线,这样的两个角叫做对顶角.
动手实践
下列各图中,∠1与∠2互为对顶角的是( )
C
判断两个角是否是对顶角的标准是什么?
动手实践
时间:2分钟
活动要求:请独立完成验证.
∵∠1+∠3=180°,∠2+∠3=180°,
∴∠1+∠3=∠2+∠3,
∴∠1=∠2.
∠1=∠2
∵直线AB与CD相交于点O,
∴∠1=∠2,∠3=∠4
对顶角相等
动手实践
活动2:特殊数量关系的角
如果两个角的和是180°,
那么称这两个角互为补角.
结论1:同角的补角相等.
∵∠1+∠3=180°, ∠2+∠3=180°
∴∠1=∠2
结论2:等角的补角相等.
∵∠1+∠3=180°,∠2+∠4=180°,
又∵∠1=∠2,∴∠3=∠4
动手实践
活动2:特殊数量关系的角
如果两个角的和是90°,那么称这两个角互为余角.
猜想:同角或等角的余角相等.
动手实践
动手实践
活动2:特殊数量关系的角
若∠ABE=∠BEF=∠ACF=∠CFE=90°,类比补角的性质来验证自己的猜想.
时间:5分钟
活动要求:小组合作,交流探讨,利用图中标出数字的角验证猜想,一人画图,一人写说理过程一人解说,一人拍照上传.
结论:同角或等角的余角相等.
小组合作
D
O
C
已知:ON与DC交于点O,∠ 1=∠2,∠DON=∠CON=90°.
问题1:有哪些角互为补角?有哪些角互为余角?
问题2:∠3与∠4有什么关系?为什么?
问题3:∠AOC与∠BOD有什么关系?为什么?
实践巩固
D
O
C
已知:ON与DC交于点O,∠ 1=∠2,∠DON=∠CON=90°.
问题1:有哪些角互为补角?有哪些角互为余角?
问题2:∠3与∠4有什么关系?为什么?
问题3:∠AOC与∠BOD有什么关系?为什么?
实践巩固
时间:3分钟
要求:完成平板推送题目. 对错误率较高的题目进行小组交流. 组内互助,总结反思.
当堂检测
通过本节课的探索与交流,你有哪些收获?
归纳小结
如图,将一个长方形纸片沿着直线EF折叠,点C落在点H处;再将∠D沿着EE折叠,使DE落在直线EH上:
问题1:∠FEG等于多少度?为什么?
问题2:上述折纸的图形中,还有哪些角互为余角?哪些角互为补角?
布置作业
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
