北师大版七年级数学下册 2.1 第2课时 垂直 教学设计
文档属性
| 名称 | 北师大版七年级数学下册 2.1 第2课时 垂直 教学设计 |
|
|
| 格式 | docx | ||
| 文件大小 | 399.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-03 14:44:16 | ||
图片预览


文档简介
第二章 相交线与平行线
第2课时 垂 线
学习目标:
1.理解垂直的有关概念、画法及性质;
2.知道垂线段和点到直线的距离两个概念,并会应用它们解决问题.(重点,难点)
教学过程:
一、情境导入
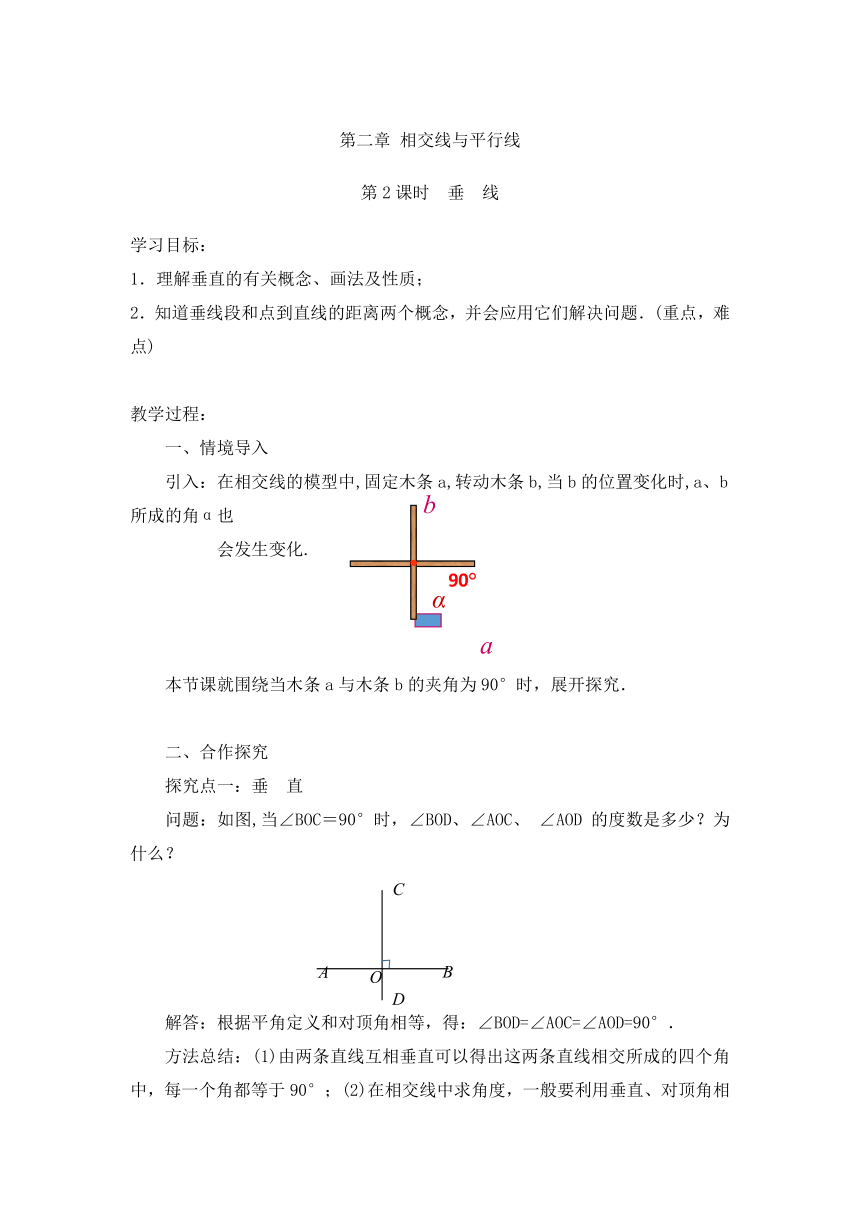
引入:在相交线的模型中,固定木条a,转动木条b,当b的位置变化时,a、b所成的角α也
会发生变化.
本节课就围绕当木条a与木条b的夹角为90°时,展开探究.
二、合作探究
探究点一:垂 直
问题:如图,当∠BOC=90°时,∠BOD、∠AOC、 ∠AOD 的度数是多少?为什么?
解答:根据平角定义和对顶角相等,得:∠BOD=∠AOC=∠AOD=90°.
方法总结:(1)由两条直线互相垂直可以得出这两条直线相交所成的四个角中,每一个角都等于90°;(2)在相交线中求角度,一般要利用垂直、对顶角相等、余角、补角等知识.
1、垂直的定义
两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相垂直.
其中的一条直线叫做另一条直线的垂线 ,它们的交点叫做垂足.
垂直的表示方法
(1)如果直线AB与直线CD垂直,那么可记作:AB⊥CD(或CD⊥AB).
(2)如果用a、b表示这两条直线,那么直线a 与直线b 垂直,可记作 a⊥b(或b⊥a).
3、符号语言
如图∵∠AOD=90°(已知) ,
∴AB⊥CD(垂直的定义)
探究二:画垂直
活动一:画、折两条互相垂直的直线
①你能用三角尺在一张白纸上画出两条互相垂直的直线吗?
②若只有直尺,你能在方格纸上画出两条互相垂直的直线吗?
③你能用纸折出两条互相垂直的直线吗
学生分组进行动手操作,讨论、总结、展示.
分析:
①用三角板画两条互相垂直的直线,是利用三角板的两条直角边.
②利用方格纸和直尺画垂直,是利用了方格纸中的每一个方格都是正方形,含有直角,从而利用直尺可以画出两条互相垂直的直线.
③用纸折垂直.有的学生可能会利用自己手中的方格纸中的垂线为折痕这出垂直,也可能会利用手中的纸是特殊形状(长方形),上下左右折叠,得到两条互相垂直的折痕;最终总结出任意一张纸,不规范也可以,先任意折叠一下,得到一个平角,然后对折平角,得到一个直角,再展开,就得到两条互相垂直的折痕.
总结:归根结底,都是先找到一个直角,然后利用垂直的定义,得到两条互相垂直的直线.
探究三:垂线的性质
活动二:画已知直线的垂线.
①画已知直线l的垂线能画几条
②过一点画已知直线l的垂线能画几条
分析:①画已知直线的垂线可以画无数条.
②过一点画已知直线的垂线,这个点可以在直线上,也可以在直线外,所以要分两种情况进行讨论.
思考:根据活动二,你能总结出什么结论呢?
垂线的性质:
在同一平面内,过一点有且只有一条直线与已知直线垂直.
注意:
1.“过一点”中的点,可以在已知直线上,也可以在已知直线外;
2.“有且只有”中,“有”指存在,“只有”指唯一性.
探究四:垂线段和点到直线的距离
通过一段视频引入:如何测量跳远的成绩?
学生先想一想,然后把这个实际问题抽象成一个数学模型,解释数学模型中每一点对应的实际含义,然后利用所学的知识,制定测量跳远成绩的方案.
小组讨论,小组代表分享讨论结果.
最终总结出:
垂线段的定义:
过直线外一点做已知直线的垂线,这个点和垂足之间的线段叫做垂线段.
垂线段的性质:
连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:垂线段最短.
点到直线的距离:
垂线段的长度,叫做点到直线的距离.
应用:
例 在灌溉时,要把河中的水引到农田P处,如何挖掘能使渠道最短?请画出图来,并说明理由.
分析:把实际问题抽象成数学模型,感受数学建模思想,即:把河近似看作一条直线m,这个问题就转化为过直线外一点P到已知直线m的最短距离.利用垂线段最短,过点P做直线m的垂线,垂线段就是最短的渠道.
三、课堂小结:
谈谈你本节课的收获.
根据学习目标,检验自己学习目标的达成度.
四、作业布置:
1.完成学案,并在课本上把本节课的关键内容进行整理标注.
2.预习本章第2课时(探索直线平行的条件)
五、板书设计
1、垂线的概念:
∵∠COB=90°,∴AB⊥CD
2、画垂直、折垂直
①利用三角尺画垂直②利用直尺在方格之中画垂直③折垂直
(学生作品展示)
3、性质:
(学生作品展示)
平面内,过一点有且只有一条直线与已知直线垂直;
直线外一点与直线上各点连接的所有线段中,垂线段最短.
4、垂线段的性质:垂线段最短.
点到直线的距离:垂线段的长.
教学反思:
本节课学习了垂线的概念和垂线的性质,垂直是相交的一种特殊情况,要说明两条相交线的位置关系,一般都是垂直.垂线的两条性质中,不要遗漏条件“在同一平面内”,以保证定理的精确性.对于垂线的概念和性质,要让学生理解记忆.
第2课时 垂 线
学习目标:
1.理解垂直的有关概念、画法及性质;
2.知道垂线段和点到直线的距离两个概念,并会应用它们解决问题.(重点,难点)
教学过程:
一、情境导入
引入:在相交线的模型中,固定木条a,转动木条b,当b的位置变化时,a、b所成的角α也
会发生变化.
本节课就围绕当木条a与木条b的夹角为90°时,展开探究.
二、合作探究
探究点一:垂 直
问题:如图,当∠BOC=90°时,∠BOD、∠AOC、 ∠AOD 的度数是多少?为什么?
解答:根据平角定义和对顶角相等,得:∠BOD=∠AOC=∠AOD=90°.
方法总结:(1)由两条直线互相垂直可以得出这两条直线相交所成的四个角中,每一个角都等于90°;(2)在相交线中求角度,一般要利用垂直、对顶角相等、余角、补角等知识.
1、垂直的定义
两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相垂直.
其中的一条直线叫做另一条直线的垂线 ,它们的交点叫做垂足.
垂直的表示方法
(1)如果直线AB与直线CD垂直,那么可记作:AB⊥CD(或CD⊥AB).
(2)如果用a、b表示这两条直线,那么直线a 与直线b 垂直,可记作 a⊥b(或b⊥a).
3、符号语言
如图∵∠AOD=90°(已知) ,
∴AB⊥CD(垂直的定义)
探究二:画垂直
活动一:画、折两条互相垂直的直线
①你能用三角尺在一张白纸上画出两条互相垂直的直线吗?
②若只有直尺,你能在方格纸上画出两条互相垂直的直线吗?
③你能用纸折出两条互相垂直的直线吗
学生分组进行动手操作,讨论、总结、展示.
分析:
①用三角板画两条互相垂直的直线,是利用三角板的两条直角边.
②利用方格纸和直尺画垂直,是利用了方格纸中的每一个方格都是正方形,含有直角,从而利用直尺可以画出两条互相垂直的直线.
③用纸折垂直.有的学生可能会利用自己手中的方格纸中的垂线为折痕这出垂直,也可能会利用手中的纸是特殊形状(长方形),上下左右折叠,得到两条互相垂直的折痕;最终总结出任意一张纸,不规范也可以,先任意折叠一下,得到一个平角,然后对折平角,得到一个直角,再展开,就得到两条互相垂直的折痕.
总结:归根结底,都是先找到一个直角,然后利用垂直的定义,得到两条互相垂直的直线.
探究三:垂线的性质
活动二:画已知直线的垂线.
①画已知直线l的垂线能画几条
②过一点画已知直线l的垂线能画几条
分析:①画已知直线的垂线可以画无数条.
②过一点画已知直线的垂线,这个点可以在直线上,也可以在直线外,所以要分两种情况进行讨论.
思考:根据活动二,你能总结出什么结论呢?
垂线的性质:
在同一平面内,过一点有且只有一条直线与已知直线垂直.
注意:
1.“过一点”中的点,可以在已知直线上,也可以在已知直线外;
2.“有且只有”中,“有”指存在,“只有”指唯一性.
探究四:垂线段和点到直线的距离
通过一段视频引入:如何测量跳远的成绩?
学生先想一想,然后把这个实际问题抽象成一个数学模型,解释数学模型中每一点对应的实际含义,然后利用所学的知识,制定测量跳远成绩的方案.
小组讨论,小组代表分享讨论结果.
最终总结出:
垂线段的定义:
过直线外一点做已知直线的垂线,这个点和垂足之间的线段叫做垂线段.
垂线段的性质:
连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:垂线段最短.
点到直线的距离:
垂线段的长度,叫做点到直线的距离.
应用:
例 在灌溉时,要把河中的水引到农田P处,如何挖掘能使渠道最短?请画出图来,并说明理由.
分析:把实际问题抽象成数学模型,感受数学建模思想,即:把河近似看作一条直线m,这个问题就转化为过直线外一点P到已知直线m的最短距离.利用垂线段最短,过点P做直线m的垂线,垂线段就是最短的渠道.
三、课堂小结:
谈谈你本节课的收获.
根据学习目标,检验自己学习目标的达成度.
四、作业布置:
1.完成学案,并在课本上把本节课的关键内容进行整理标注.
2.预习本章第2课时(探索直线平行的条件)
五、板书设计
1、垂线的概念:
∵∠COB=90°,∴AB⊥CD
2、画垂直、折垂直
①利用三角尺画垂直②利用直尺在方格之中画垂直③折垂直
(学生作品展示)
3、性质:
(学生作品展示)
平面内,过一点有且只有一条直线与已知直线垂直;
直线外一点与直线上各点连接的所有线段中,垂线段最短.
4、垂线段的性质:垂线段最短.
点到直线的距离:垂线段的长.
教学反思:
本节课学习了垂线的概念和垂线的性质,垂直是相交的一种特殊情况,要说明两条相交线的位置关系,一般都是垂直.垂线的两条性质中,不要遗漏条件“在同一平面内”,以保证定理的精确性.对于垂线的概念和性质,要让学生理解记忆.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
