20.3 综合与实践 体重指数 特色训练题(含答案)
文档属性
| 名称 | 20.3 综合与实践 体重指数 特色训练题(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 81.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-02 00:00:00 | ||
图片预览

文档简介
20.3 综合与实践 体重指数(特色训练题)
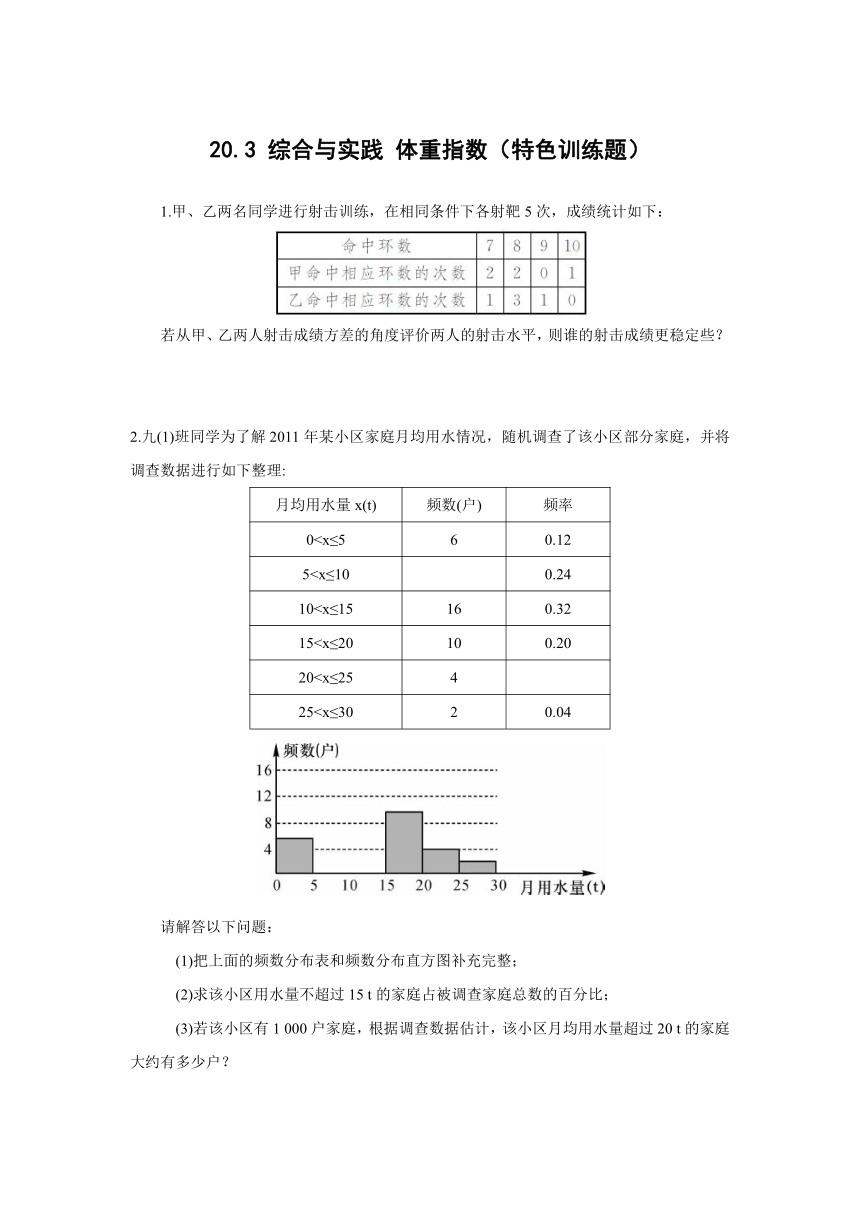
1.甲、乙两名同学进行射击训练,在相同条件下各射靶5次,成绩统计如下:
若从甲、乙两人射击成绩方差的角度评价两人的射击水平,则谁的射击成绩更稳定些?
2.九(1)班同学为了解2011年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:
月均用水量x(t) 频数(户) 频率
0510152025请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)求该小区用水量不超过15 t的家庭占被调查家庭总数的百分比;
(3)若该小区有1 000户家庭,根据调查数据估计,该小区月均用水量超过20 t的家庭大约有多少户?
参考答案
1.解:甲、乙两人射击成绩的平均成绩分别为:
甲=(7×2+8×2+10×1)=8,
乙=(7×1+8×3+9×1)=8,
s2甲=[2×(7-8)2+2×(8-8)2+(10-8)2]=1.2,
s2乙=[(7-8)2+3×(8-8)2+(9-8)2]=0.4.
∵s2甲>s2乙,∴乙同学的射击成绩比较稳定.
点拨:在平均数相等时,方差越小,数据越稳定.
2.解:(1)根据频数分布表可知0<x≤5频数为6,频率为0.12,则
6÷0.12=50,50×0.24=12(户),
4÷50=0.08,
故表格从上往下依次是:12户和0.08;
频数分布直方图补充如下:
(2)用水量不超过15吨是前三组,(0.12+0.24+0.32)×100%=68%;
(3)1000×(0.04+0.08)=120(户).
1.甲、乙两名同学进行射击训练,在相同条件下各射靶5次,成绩统计如下:
若从甲、乙两人射击成绩方差的角度评价两人的射击水平,则谁的射击成绩更稳定些?
2.九(1)班同学为了解2011年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:
月均用水量x(t) 频数(户) 频率
0
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)求该小区用水量不超过15 t的家庭占被调查家庭总数的百分比;
(3)若该小区有1 000户家庭,根据调查数据估计,该小区月均用水量超过20 t的家庭大约有多少户?
参考答案
1.解:甲、乙两人射击成绩的平均成绩分别为:
甲=(7×2+8×2+10×1)=8,
乙=(7×1+8×3+9×1)=8,
s2甲=[2×(7-8)2+2×(8-8)2+(10-8)2]=1.2,
s2乙=[(7-8)2+3×(8-8)2+(9-8)2]=0.4.
∵s2甲>s2乙,∴乙同学的射击成绩比较稳定.
点拨:在平均数相等时,方差越小,数据越稳定.
2.解:(1)根据频数分布表可知0<x≤5频数为6,频率为0.12,则
6÷0.12=50,50×0.24=12(户),
4÷50=0.08,
故表格从上往下依次是:12户和0.08;
频数分布直方图补充如下:
(2)用水量不超过15吨是前三组,(0.12+0.24+0.32)×100%=68%;
(3)1000×(0.04+0.08)=120(户).
