华东师大版数学八年级下册 19.1矩形 19.1.2 矩形的判定 课件 (共15张PPT)
文档属性
| 名称 | 华东师大版数学八年级下册 19.1矩形 19.1.2 矩形的判定 课件 (共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 244.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-03 00:00:00 | ||
图片预览


文档简介
(共15张PPT)
数学 八年级下册 华师版
第19章 矩形、菱形与正方形
19.1 矩形19.1.2 矩形的判定
知识点 :有一个角是直角的平行四边形是矩形
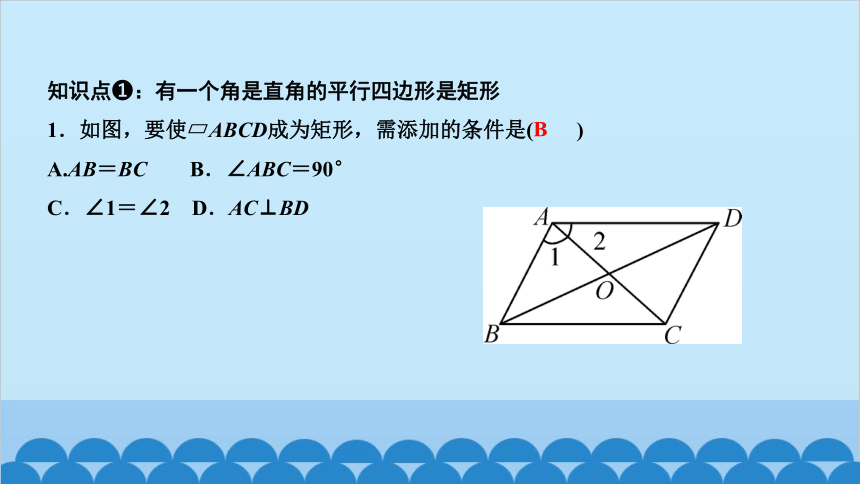
1.如图,要使 ABCD成为矩形,需添加的条件是( )
A.AB=BC B.∠ABC=90°
C.∠1=∠2 D.AC⊥BD
B
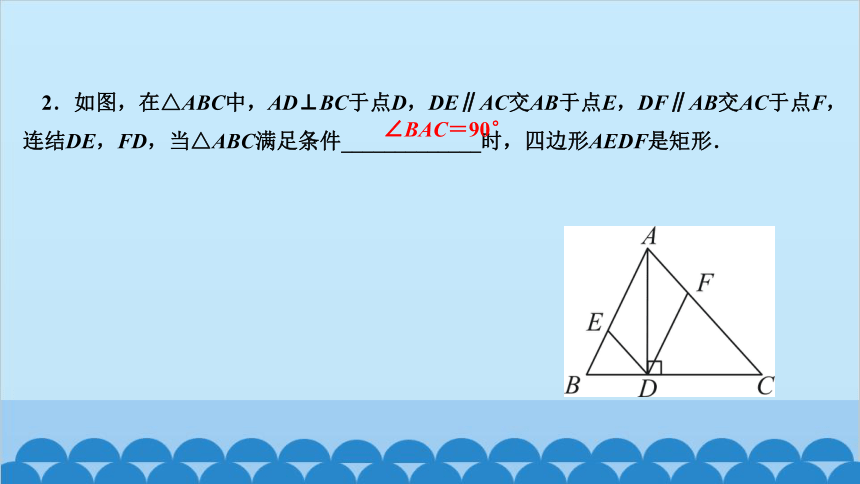
2.如图,在△ABC中,AD⊥BC于点D,DE∥AC交AB于点E,DF∥AB交AC于点F,连结DE,FD,当△ABC满足条件_____________时,四边形AEDF是矩形.
∠BAC=90°
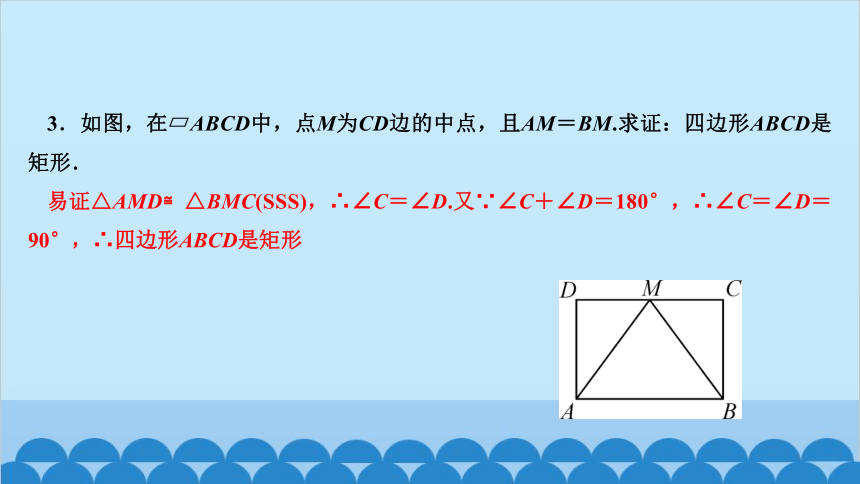
3.如图,在 ABCD中,点M为CD边的中点,且AM=BM.求证:四边形ABCD是矩形.
易证△AMD≌△BMC(SSS),∴∠C=∠D.又∵∠C+∠D=180°,∴∠C=∠D=90°,∴四边形ABCD是矩形
知识点 :矩形的判定定理1——有三个角是直角的四边形是矩形
4.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的4位同学拟定的方案,其中正确的是( )
A.测量对角线是否相互平分
B.测量两组对边是否分别相等
C.测量一组对角是否都为直角
D.测量四边形其中的三个角是否都为直角
D
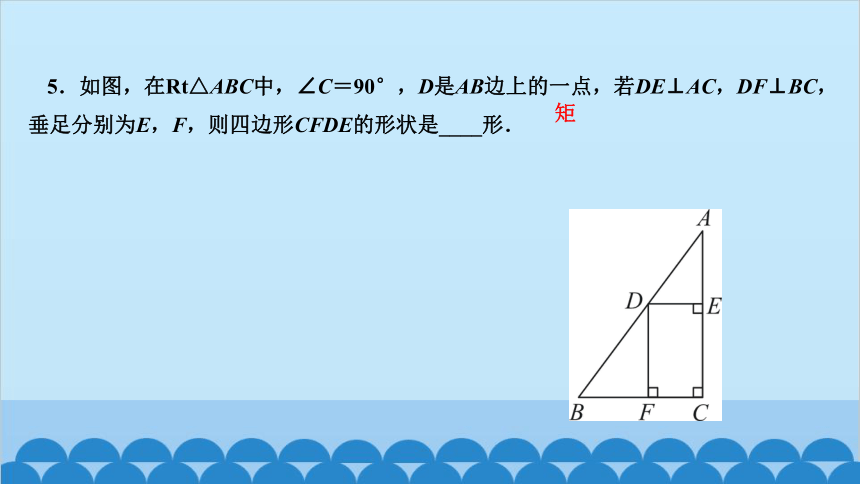
5.如图,在Rt△ABC中,∠C=90°,D是AB边上的一点,若DE⊥AC,DF⊥BC,垂足分别为E,F,则四边形CFDE的形状是____形.
矩
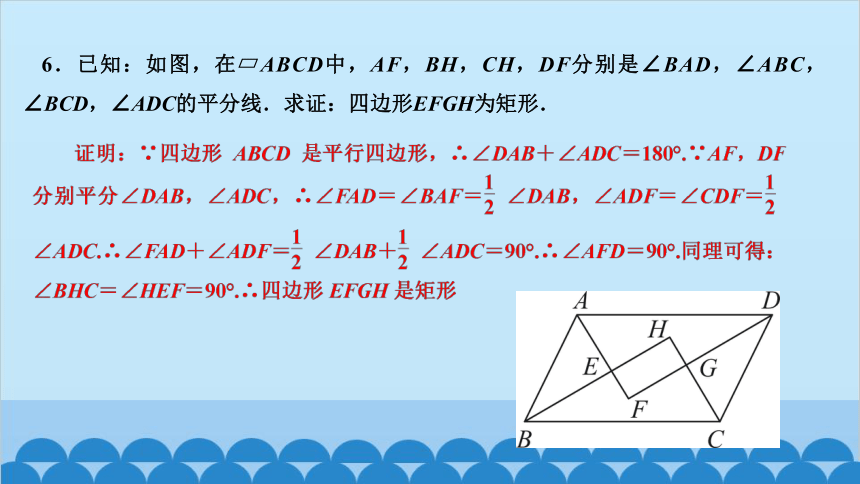
6.已知:如图,在 ABCD中,AF,BH,CH,DF分别是∠BAD,∠ABC,∠BCD,∠ADC的平分线.求证:四边形EFGH为矩形.
A
8.(聊城中考)如图,在 ABCD中,E为BC的中点,连结AE并延长交DC的延长线于点F,连结BF,AC,若AD=AF,求证:四边形ABFC是矩形.
证明:∵四边形ABCD是平行四边形,∴AB∥CD,AD=BC,∴∠BAE=∠CFE,∠ABE=∠FCE,∵E为BC的中点,∴EB=EC,∴△ABE≌△FCE(AAS),∴AB=CF.∵AB∥CF,∴四边形ABFC是平行四边形,∵AD=AF,∴BC=AF,∴四边形ABFC是矩形
9.(南阳唐河县期末)如图,四边形ABCD为平行四边形,延长AD到点E,使DE=AD,连结EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
A.AB=BE B.BE⊥DC
C.∠ADB=90° D.CE⊥DE
B
10.在四边形ABCD中,对角线AC,BD交于点O,从 ①AB=CD;②AB∥CD;③OA=OC;④OB=OD;⑤AC=BD;⑥∠ABC=90°,这六个条件中,可选取三个推出四边形ABCD是矩形,如①②⑤→四边形ABCD是矩形.请再写出符合要求的两个组合:_________;______________________.
①②⑥
③④⑥(答案不唯一)
11.(安顺中考)如图,在Rt△ABC中,∠BAC=90°,且BA=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连结MN,则线段MN的最小值为____.
12.(2021·连云港)如图,点C是BE的中点,四边形ABCD是平行四边形.
(1)求证:四边形ACED是平行四边形;
(2)如果AB=AE,求证:四边形ACED是矩形.
证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC,且AD=BC.∵点C是BE的中点,∴BC=CE,∴AD=CE,∵AD∥CE,∴四边形ACED是平行四边形
(2)∵四边形ABCD是平行四边形,∴AB=DC,∵AB=AE,∴DC=AE,∵四边形ACED是平行四边形,∴四边形ACED是矩形
13.如图,在△ABC中,点O是边AC上一个动点,过点O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
数学 八年级下册 华师版
第19章 矩形、菱形与正方形
19.1 矩形19.1.2 矩形的判定
知识点 :有一个角是直角的平行四边形是矩形
1.如图,要使 ABCD成为矩形,需添加的条件是( )
A.AB=BC B.∠ABC=90°
C.∠1=∠2 D.AC⊥BD
B
2.如图,在△ABC中,AD⊥BC于点D,DE∥AC交AB于点E,DF∥AB交AC于点F,连结DE,FD,当△ABC满足条件_____________时,四边形AEDF是矩形.
∠BAC=90°
3.如图,在 ABCD中,点M为CD边的中点,且AM=BM.求证:四边形ABCD是矩形.
易证△AMD≌△BMC(SSS),∴∠C=∠D.又∵∠C+∠D=180°,∴∠C=∠D=90°,∴四边形ABCD是矩形
知识点 :矩形的判定定理1——有三个角是直角的四边形是矩形
4.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的4位同学拟定的方案,其中正确的是( )
A.测量对角线是否相互平分
B.测量两组对边是否分别相等
C.测量一组对角是否都为直角
D.测量四边形其中的三个角是否都为直角
D
5.如图,在Rt△ABC中,∠C=90°,D是AB边上的一点,若DE⊥AC,DF⊥BC,垂足分别为E,F,则四边形CFDE的形状是____形.
矩
6.已知:如图,在 ABCD中,AF,BH,CH,DF分别是∠BAD,∠ABC,∠BCD,∠ADC的平分线.求证:四边形EFGH为矩形.
A
8.(聊城中考)如图,在 ABCD中,E为BC的中点,连结AE并延长交DC的延长线于点F,连结BF,AC,若AD=AF,求证:四边形ABFC是矩形.
证明:∵四边形ABCD是平行四边形,∴AB∥CD,AD=BC,∴∠BAE=∠CFE,∠ABE=∠FCE,∵E为BC的中点,∴EB=EC,∴△ABE≌△FCE(AAS),∴AB=CF.∵AB∥CF,∴四边形ABFC是平行四边形,∵AD=AF,∴BC=AF,∴四边形ABFC是矩形
9.(南阳唐河县期末)如图,四边形ABCD为平行四边形,延长AD到点E,使DE=AD,连结EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
A.AB=BE B.BE⊥DC
C.∠ADB=90° D.CE⊥DE
B
10.在四边形ABCD中,对角线AC,BD交于点O,从 ①AB=CD;②AB∥CD;③OA=OC;④OB=OD;⑤AC=BD;⑥∠ABC=90°,这六个条件中,可选取三个推出四边形ABCD是矩形,如①②⑤→四边形ABCD是矩形.请再写出符合要求的两个组合:_________;______________________.
①②⑥
③④⑥(答案不唯一)
11.(安顺中考)如图,在Rt△ABC中,∠BAC=90°,且BA=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连结MN,则线段MN的最小值为____.
12.(2021·连云港)如图,点C是BE的中点,四边形ABCD是平行四边形.
(1)求证:四边形ACED是平行四边形;
(2)如果AB=AE,求证:四边形ACED是矩形.
证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC,且AD=BC.∵点C是BE的中点,∴BC=CE,∴AD=CE,∵AD∥CE,∴四边形ACED是平行四边形
(2)∵四边形ABCD是平行四边形,∴AB=DC,∵AB=AE,∴DC=AE,∵四边形ACED是平行四边形,∴四边形ACED是矩形
13.如图,在△ABC中,点O是边AC上一个动点,过点O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
