人教版九年级数学下册 第二十七章 相似(word版 含答案)
文档属性
| 名称 | 人教版九年级数学下册 第二十七章 相似(word版 含答案) | 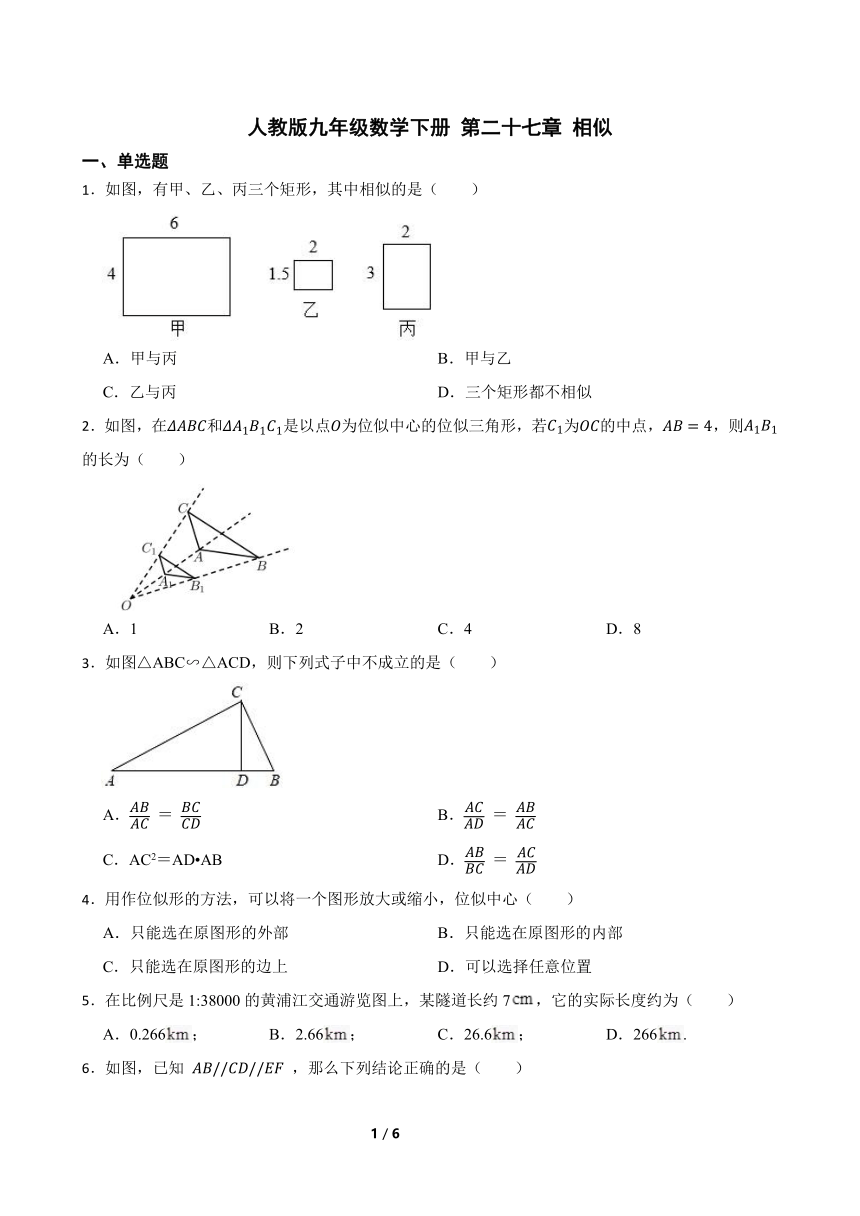 | |
| 格式 | docx | ||
| 文件大小 | 88.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-03 15:28:12 | ||
图片预览


文档简介
人教版九年级数学下册 第二十七章 相似
一、单选题
1.如图,有甲、乙、丙三个矩形,其中相似的是( )
A.甲与丙 B.甲与乙
C.乙与丙 D.三个矩形都不相似
2.如图,在和是以点为位似中心的位似三角形,若为的中点,,则的长为( )
A.1 B.2 C.4 D.8
3.如图△ABC∽△ACD,则下列式子中不成立的是( )
A. = B. =
C.AC2=AD AB D. =
4.用作位似形的方法,可以将一个图形放大或缩小,位似中心( )
A.只能选在原图形的外部 B.只能选在原图形的内部
C.只能选在原图形的边上 D.可以选择任意位置
5.在比例尺是1:38000的黄浦江交通游览图上,某隧道长约7,它的实际长度约为( )
A.0.266; B.2.66; C.26.6; D.266.
6.如图,已知 ,那么下列结论正确的是( )
A. B. C. D.
7.若△ABC∽△DEF,且S△ABC:S△DEF=3:4,则其相似比为( )
A.3:4 B.4:3 C. :2 D.2:
8.如图所示,在△ABC中,DE∥BC,若AD=1,DB=2,则 的值为( )
A. B. C. D.
9.已知△ABC∽△DEF,且△ABC的面积与△DEF的面积之比为4:9,则AB:DE=( )
A.4:9 B.2:3 C.16:81 D.9:4
10.如图所示,为估算某河的宽度,在河对岸的边上选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上,若测得BE=20m,EC=10m,CD=20m,则河的宽度AB的长为( )
A.60m B.40m C.30m D.20m
二、填空题
11.如果3x=4y,那么 = .
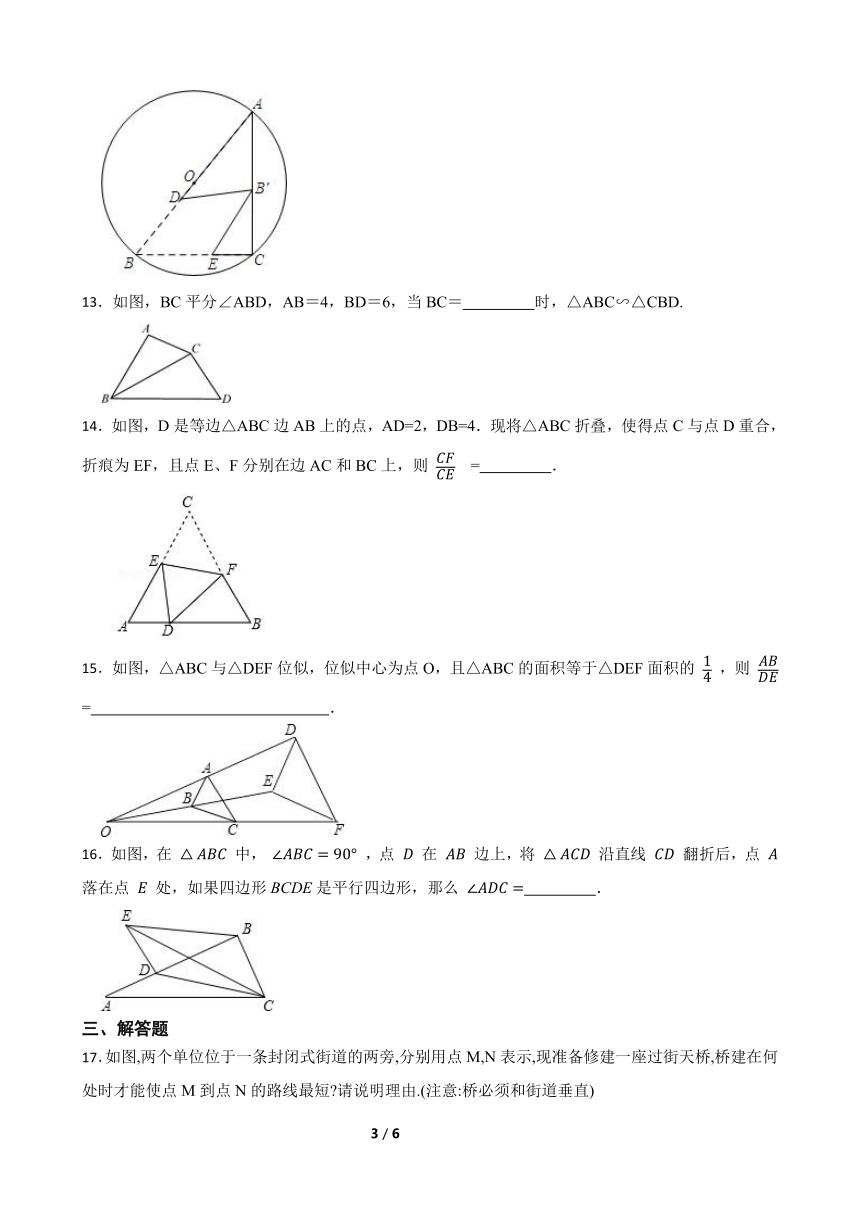
12.如图,△ABC内接于⊙O.AB为⊙O的直径,BC=3,AB=5,D、E分别是边AB、BC上的两个动点(不与端点A、B、C重合),将△BDE沿DE折叠,点B的对应点B′恰好落在线段AC上(包含端点A、C),若△ADB′为等腰三角形,则AD的长为 .
13.如图,BC平分∠ABD,AB=4,BD=6,当BC= 时,△ABC∽△CBD.
14.如图,D是等边△ABC边AB上的点,AD=2,DB=4.现将△ABC折叠,使得点C与点D重合,折痕为EF,且点E、F分别在边AC和BC上,则 = .
15.如图,△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的 ,则 = .
16.如图,在 中, ,点 在 边上,将 沿直线 翻折后,点 落在点 处,如果四边形BCDE是平行四边形,那么 .
三、解答题
17.如图,两个单位位于一条封闭式街道的两旁,分别用点M,N表示,现准备修建一座过街天桥,桥建在何处时才能使点M到点N的路线最短 请说明理由.(注意:桥必须和街道垂直)
18.如图,在△ABC中,D为AC边上一点,∠DBC=∠A.
(1)求证:△BCD∽△ABC;
(2)如果BC=,AC=3,求CD的长.
19.如图,在△ABC中,∠C=90°,∠B=30°,AB的垂直平分线交BC于D,垂足为E,BD=4cm.求AC的长.
20.如图,在△ABC中,AC=8厘米,BC=16厘米,点P从点A出发,沿着AC边向点C以1cm/s的速度运动,点Q从点C出发,沿着CB边向点B以2cm/s的速度运动,如果P与Q同时出发,经过几秒△PQC和△ABC相似?
答案解析部分
1.【答案】A
2.【答案】B
3.【答案】D
4.【答案】D
5.【答案】B
6.【答案】A
7.【答案】C
8.【答案】C
9.【答案】B
10.【答案】B
11.【答案】
12.【答案】 或 或
13.【答案】
14.【答案】
15.【答案】
16.【答案】135°
17.【答案】解: ①作NE⊥AB于点E,交CD于点F;
②在NE上截取NN'=EF;
③连接MN',交AB于点P;
④过点P作PQ⊥AB,交CD于点Q,如图,则PQ为过街天桥应建的位置.
理由:如图,连接QN.
∵PQ⊥AB,NE⊥AB,∴PQ∥NE.
又∵NN'=EF,EF=PQ,
∴PQ=NN'(相当于将PQ平移到NN').
∴QN=PN'.
∴MP+PN'最短(两点之间线段最短),PQ为定值.
∴桥建在PQ处时才能使点M到点N的路线最短.
18.【答案】(1)证明:∵∠DBC=∠A,∠C=∠C,∴△ABCD∽△ABC;(2)解:∵△BCD∽△ABC,∴,∴=,∴CD=2.
19.【答案】解:如图,连接AD, ∵ED是AB的垂直平分线, ∴AD=BD=4, ∴∠BAD=∠B=30°, ∴∠DAC=30°, ∵DC= AD=2, ∴AC= . 故答案是 .
20.【答案】解:设经过x秒,两三角形相似,
则CP=AC﹣AP=8﹣x,CQ=2x,
①当CP与CA是对应边时, ,
即 ,
解得x=4秒
②当CP与BC是对应边时, ,
即 ,
解得x= 秒;
故经过4或 秒,两个三角形相似.
1 / 1
一、单选题
1.如图,有甲、乙、丙三个矩形,其中相似的是( )
A.甲与丙 B.甲与乙
C.乙与丙 D.三个矩形都不相似
2.如图,在和是以点为位似中心的位似三角形,若为的中点,,则的长为( )
A.1 B.2 C.4 D.8
3.如图△ABC∽△ACD,则下列式子中不成立的是( )
A. = B. =
C.AC2=AD AB D. =
4.用作位似形的方法,可以将一个图形放大或缩小,位似中心( )
A.只能选在原图形的外部 B.只能选在原图形的内部
C.只能选在原图形的边上 D.可以选择任意位置
5.在比例尺是1:38000的黄浦江交通游览图上,某隧道长约7,它的实际长度约为( )
A.0.266; B.2.66; C.26.6; D.266.
6.如图,已知 ,那么下列结论正确的是( )
A. B. C. D.
7.若△ABC∽△DEF,且S△ABC:S△DEF=3:4,则其相似比为( )
A.3:4 B.4:3 C. :2 D.2:
8.如图所示,在△ABC中,DE∥BC,若AD=1,DB=2,则 的值为( )
A. B. C. D.
9.已知△ABC∽△DEF,且△ABC的面积与△DEF的面积之比为4:9,则AB:DE=( )
A.4:9 B.2:3 C.16:81 D.9:4
10.如图所示,为估算某河的宽度,在河对岸的边上选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上,若测得BE=20m,EC=10m,CD=20m,则河的宽度AB的长为( )
A.60m B.40m C.30m D.20m
二、填空题
11.如果3x=4y,那么 = .
12.如图,△ABC内接于⊙O.AB为⊙O的直径,BC=3,AB=5,D、E分别是边AB、BC上的两个动点(不与端点A、B、C重合),将△BDE沿DE折叠,点B的对应点B′恰好落在线段AC上(包含端点A、C),若△ADB′为等腰三角形,则AD的长为 .
13.如图,BC平分∠ABD,AB=4,BD=6,当BC= 时,△ABC∽△CBD.
14.如图,D是等边△ABC边AB上的点,AD=2,DB=4.现将△ABC折叠,使得点C与点D重合,折痕为EF,且点E、F分别在边AC和BC上,则 = .
15.如图,△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的 ,则 = .
16.如图,在 中, ,点 在 边上,将 沿直线 翻折后,点 落在点 处,如果四边形BCDE是平行四边形,那么 .
三、解答题
17.如图,两个单位位于一条封闭式街道的两旁,分别用点M,N表示,现准备修建一座过街天桥,桥建在何处时才能使点M到点N的路线最短 请说明理由.(注意:桥必须和街道垂直)
18.如图,在△ABC中,D为AC边上一点,∠DBC=∠A.
(1)求证:△BCD∽△ABC;
(2)如果BC=,AC=3,求CD的长.
19.如图,在△ABC中,∠C=90°,∠B=30°,AB的垂直平分线交BC于D,垂足为E,BD=4cm.求AC的长.
20.如图,在△ABC中,AC=8厘米,BC=16厘米,点P从点A出发,沿着AC边向点C以1cm/s的速度运动,点Q从点C出发,沿着CB边向点B以2cm/s的速度运动,如果P与Q同时出发,经过几秒△PQC和△ABC相似?
答案解析部分
1.【答案】A
2.【答案】B
3.【答案】D
4.【答案】D
5.【答案】B
6.【答案】A
7.【答案】C
8.【答案】C
9.【答案】B
10.【答案】B
11.【答案】
12.【答案】 或 或
13.【答案】
14.【答案】
15.【答案】
16.【答案】135°
17.【答案】解: ①作NE⊥AB于点E,交CD于点F;
②在NE上截取NN'=EF;
③连接MN',交AB于点P;
④过点P作PQ⊥AB,交CD于点Q,如图,则PQ为过街天桥应建的位置.
理由:如图,连接QN.
∵PQ⊥AB,NE⊥AB,∴PQ∥NE.
又∵NN'=EF,EF=PQ,
∴PQ=NN'(相当于将PQ平移到NN').
∴QN=PN'.
∴MP+PN'最短(两点之间线段最短),PQ为定值.
∴桥建在PQ处时才能使点M到点N的路线最短.
18.【答案】(1)证明:∵∠DBC=∠A,∠C=∠C,∴△ABCD∽△ABC;(2)解:∵△BCD∽△ABC,∴,∴=,∴CD=2.
19.【答案】解:如图,连接AD, ∵ED是AB的垂直平分线, ∴AD=BD=4, ∴∠BAD=∠B=30°, ∴∠DAC=30°, ∵DC= AD=2, ∴AC= . 故答案是 .
20.【答案】解:设经过x秒,两三角形相似,
则CP=AC﹣AP=8﹣x,CQ=2x,
①当CP与CA是对应边时, ,
即 ,
解得x=4秒
②当CP与BC是对应边时, ,
即 ,
解得x= 秒;
故经过4或 秒,两个三角形相似.
1 / 1
