华东师大版九年级数学上册第24章解直角三角形达标检测卷(Word版,附答案)
文档属性
| 名称 | 华东师大版九年级数学上册第24章解直角三角形达标检测卷(Word版,附答案) |  | |
| 格式 | doc | ||
| 文件大小 | 258.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-03 22:52:34 | ||
图片预览



文档简介
华东师大版九年级数学上册 第24章 达标检测卷
(限时: 120分钟 满分: 100分)
班级: 姓名: 得分:
一、选择题(每题3分,共24分)
1.在△ABC中,∠C=90°,AB=5,BC=3,则cos A的值是( )
A. B. . D.
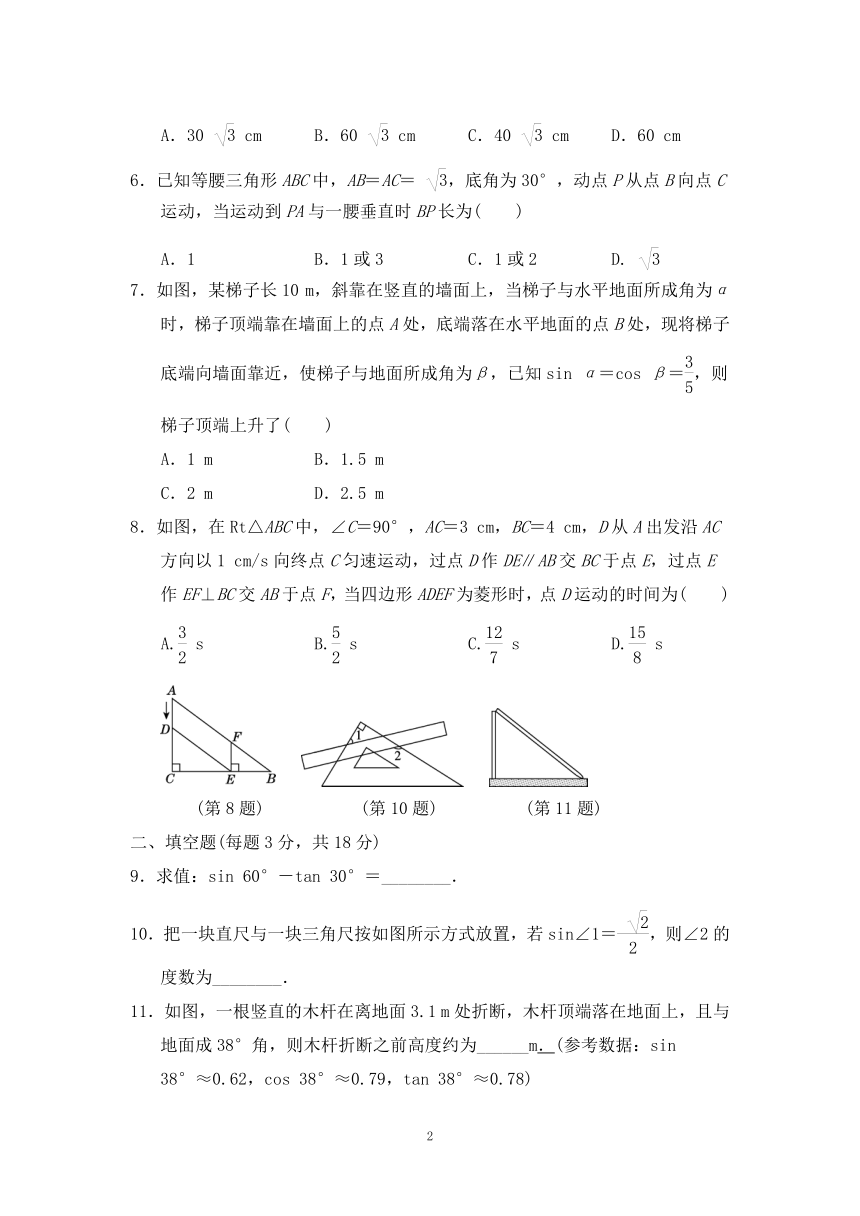
2.如图,一艘船向东航行,上午8时到达A处,测得一灯塔B在船的北偏东30°方向,且距离船48 n mile;上午11时到达C处,测得灯塔在船的正北方向,则这艘船航行的速度为( )
A.24 n mile/h B.8n mile/h
C.24 n mile/h D.8 n mile/h
INCLUDEPICTURE"M19.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M19.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M19.tif" \* MERGEFORMATINET INCLUDEPICTURE"M20.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M20.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M20.tif" \* MERGEFORMATINET INCLUDEPICTURE"M21.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M21.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M21.tif" \* MERGEFORMATINET
(第2题) (第5题) (第7题)
3.点M(-sin 60°,cos 60°)关于x轴对称的点的坐标是( )
A. B. C. D.
4.在△ABC中,AB=12,AC=13,cos B=,则BC=( )
A.7 B.8 C.8或17 D.7或17
5. 如图是我们经常看到的一种折叠桌子的示意图,它是由下面的支架AD,BC与桌面构成的,已知OA=OB=OC=OD=20 cm,∠COD=60°,则点A到地面(CD所在的平面)的距离是( )
A.30 cm B.60 cm C.40 cm D.60 cm
6.已知等腰三角形ABC中,AB=AC=,底角为30°,动点P从点B向点C运动,当运动到PA与一腰垂直时BP长为( )
A.1 B.1或3 C.1或2 D.
7.如图,某梯子长10 m,斜靠在竖直的墙面上,当梯子与水平地面所成角为α时,梯子顶端靠在墙面上的点A处,底端落在水平地面的点B处,现将梯子底端向墙面靠近,使梯子与地面所成角为β,已知sin α=cos β=,则梯子顶端上升了( )
A.1 m B.1.5 m
C.2 m D.2.5 m
8.如图,在Rt△ABC中,∠C=90°,AC=3 cm,BC=4 cm,D从A出发沿AC方向以1 cm/s向终点C匀速运动,过点D作DE∥AB交BC于点E,过点E作EF⊥BC交AB于点F,当四边形ADEF为菱形时,点D运动的时间为( )
A. s B. s C. s D. s
INCLUDEPICTURE"M22.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M22.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M22.tif" \* MERGEFORMATINET INCLUDEPICTURE"M23.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M23.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M23.tif" \* MERGEFORMATINET INCLUDEPICTURE"M24.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M24.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M24.tif" \* MERGEFORMATINET
(第8题) (第10题) (第11题)
二、填空题(每题3分,共18分)
9.求值:sin 60°-tan 30°=________.
10.把一块直尺与一块三角尺按如图所示方式放置,若sin∠1=,则∠2的度数为________.
11.如图,一根竖直的木杆在离地面3.1 m处折断,木杆顶端落在地面上,且与地面成38°角,则木杆折断之前高度约为______m.(参考数据:sin 38°≈0.62,cos 38°≈0.79,tan 38°≈0.78)
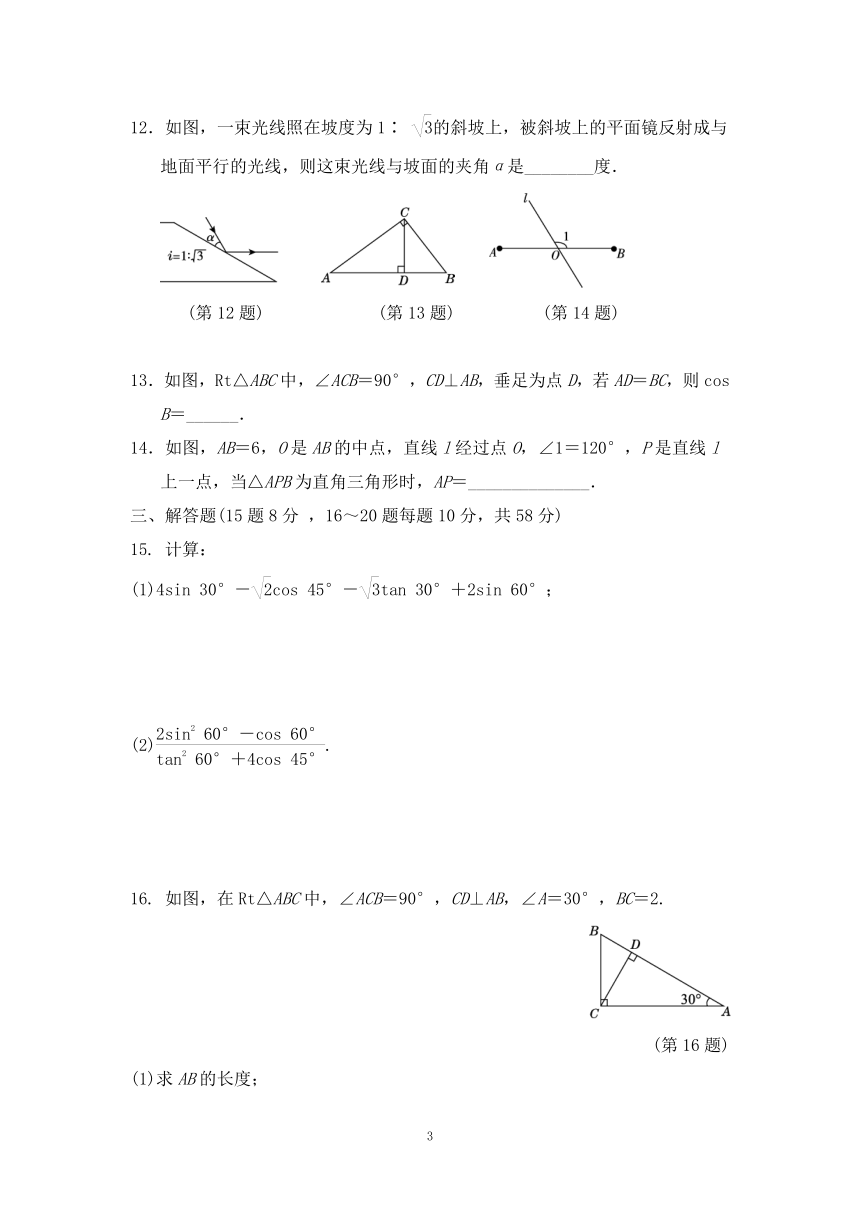
12.如图,一束光线照在坡度为1∶ 的斜坡上,被斜坡上的平面镜反射成与地面平行的光线,则这束光线与坡面的夹角α是________度.
INCLUDEPICTURE"HS30.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\HS30.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\HS30.tif" \* MERGEFORMATINET INCLUDEPICTURE"M25.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M25.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M25.tif" \* MERGEFORMATINET INCLUDEPICTURE"J30.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\J30.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\J30.tif" \* MERGEFORMATINET
(第12题) (第13题) (第14题)
13.如图,Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,若AD=BC,则cos B=______.
14.如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点,当△APB为直角三角形时,AP=______________.
三、解答题(15题8分 ,16~20题每题10分,共58分)
15. 计算:
(1)4sin 30°-cos 45°-tan 30°+2sin 60°;
(2).
16. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,∠A=30°,BC=2.
INCLUDEPICTURE"M26.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M26.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M26.tif" \* MERGEFORMATINET
(第16题)
(1)求AB的长度;
(2)求△ABC的面积;
(3)求CD的长度.
17. 小明想测量一棵树AB的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长BF为8 m,坡面上的影长CF为4 m.已知斜坡的坡角为30°,同一时刻,一根长为1 m且垂直于地面放置的标杆在地面上的影长为2 m,求树AB的高度.
INCLUDEPICTURE"二改+43.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\二改+43.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\二改+43.tif" \* MERGEFORMATINET
(第17题)
18. 如图,为测量某观光塔的高度,一人先在附近一楼房的底端点A处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端点B处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45 m,求观光塔的高CD是多少米.
INCLUDEPICTURE"M27.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M27.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M27.tif" \* MERGEFORMATINET
(第18题)
19. 定义:在△ABC中,我们把∠A的对边与∠C 的对边的比叫做∠A的邻弦,记作thi A,即thi A==.请解答下列问题:
已知在△ABC中,∠C=30°.
(1)若∠A=45°,求thi A的值;
(2)若thi A= ,则∠A=________;
(3)若∠A是锐角,探究thi A与sin A的数量关系.
20.如图,在四边形ABCD中,AB∥DC,AB≠CD,∠BCD=90°,且AB=1,BC=2,tan ∠ADC=2.
(1)求证:DC=BC;
(2)E是四边形ABCD内一点,F是四边形ABCD外一点,且∠EDC=∠FBC,DE=BF,试判断△ECF的形状,并证明你的结论;
(3)在(2)的条件下,当BE∶CE=1∶2,∠BEC=135°时,求sin ∠BFE.
INCLUDEPICTURE"HS39.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\HS39.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\HS39.tif" \* MERGEFORMATINET
(第20题)
答案
一、1.D 2.D 3.B 4.D 5.D 6.C 7.C
8.D 点拨:设经过t s后,四边形ADEF是菱形,
∴AD=DE=t cm,DE∥AB,
∴CD=(3-t)cm,∠ABC=∠DEC,
∵∠C=90°,AC=3 cm,BC=4 cm,
∴AB===5(cm).
∵sin∠DEC=sin∠ABC==,
∴=,∴t=.
二、9. 10.135° 11.8.1 12.30
13. 点拨:设AD=BC=x,∵∠ACB=90°,CD⊥AB,
∴∠A+∠ACD=∠ACD+∠BCD=90°,∴∠A=∠BCD.又∠B=∠B,∴△ABC ∽△CBD,∴=,即=,∴BD=x(负根已经舍弃),∴cos B==.
14.3或3或3 点拨:当∠APB=90°时,分两种情况讨论.情况一:如图①,∵O是AB的中点,∠APB=90°,∴PO=BO=AO,∵∠1=120°,∴∠AOP=60°,∴△AOP为等边三角形,∴AP=OA=AB=3;情况二:如图②,∵O是AB的中点,∠APB=90°,∴PO=BO,∵∠1=120°,∴∠BOP=60°,∴△BOP为等边三角形,∴∠OBP=60°,∴AP=AB·sin 60°=6×=3;当∠BAP=90°时,如图③,∵O是AB的中点,∴OA=OB=AB=3.∵∠1=120°,∴∠AOP=60°,∴AP=OA·tan∠AOP=3×=3;当∠ABP=90°时,如图④,∵∠1=120°,∴∠BOP=60°.∵O是AB的中点,∴OB=AB=3,∴PB=OB·tan∠BOP=3×=3,
∴PA==3,故答案为3或3或3.
INCLUDEPICTURE"DA24-2.tif" INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\DA24-2.tif" \* MERGEFORMATINET (第14题)
三、15.解:(1)原式=4×-×-×+2×=2-1-1+=.
(2)原式===3-2.
16.解:(1)∵∠ACB=90°,∠A=30°,∴AB=2BC=4.
(2)在Rt△ABC中,∠ACB=90°,AB=4,BC=2,
根据勾股定理,得AC===2,
∴S△ABC=×BC×AC=×2×2=2.
(3)∵S△ABC=×AB×CD=2,AB=4,
∴×4×CD=2,解得CD=.
17.解:延长AC交BF延长线于点D,作CE⊥BD于点E,
在Rt△CFE中,∠CFE=30°,CF=4 m,∴CE=2 m,EF=4cos 30°=4×=2(m).
∵同一时刻,一根长为1 m且垂直于地面放置的标杆在地面上的影长为2 m,∴CE∶DE=1∶2,AB∶BD=1∶2,
∴DE=4 m,∴BD=BF+EF+ED=(12+2)m,
∴AB=BD=(12+2)=+6(m).
答:树AB的高度为(+6)m.
18.解:由题意得∠ADB=30°,∠CAD=60°,
在Rt△ABD中,AD==45 m.
在Rt△ACD中,CD=AD·tan 60°=45×=135(m).
答:观光塔的高CD是135 m.
19.解:(1)如图,在△ABC中,∠C=30°,∠A=45°.
作BH⊥AC,垂足为H.在Rt△BHC中,sin C==,
即BC=2BH.
在Rt△BHA中,sin A==,
INCLUDEPICTURE"DA24-6.tif" INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\DA24-6.tif" \* MERGEFORMATINET
(第19题)
即AB=BH.∴thi A==.
(2)60°或120°
(3)如图,在△ABC中,
∠C=30°,thi A=.
在Rt△BHA中,sin A=.在Rt△BHC中,sin C==,即BC=2BH.∴thi A=,即thi A=2sinA.
20.(1)证明:如图,过点A作DC的垂线AM,交DC于点M,∵AB∥DC,∠BCD=90°,∴∠ABC=90°,
易知四边形ABCM为矩形,∴AM=BC=2,MC=AB=1.
∵tan ∠ADC==2,∴DM=AM=1.
∴DC=DM+MC=2,∴DC=BC.
INCLUDEPICTURE"HS66.tif" INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\HS66.tif" \* MERGEFORMATINET
(第20题)
(2)解:△ECF是等腰直角三角形.
证明:如图,∵DE=BF,∠EDC=∠FBC,DC=BC,
∴△DEC ≌△BFC,∴∠1=∠3,EC=FC.
∴∠3+∠2=∠1+∠2=90°.
∴△ECF为等腰直角三角形.
(3)解:在(2)的条件下,∠CEF=45°,
∵∠BEC=135°,∴∠BEF=135°-45°=90°.
∵BE∶CE=1∶2,∴设BE=k,CE=2k,易知EF=2k,∴BF===3k.
在Rt△BEF中,sin ∠BFE===.
PAGE
(限时: 120分钟 满分: 100分)
班级: 姓名: 得分:
一、选择题(每题3分,共24分)
1.在△ABC中,∠C=90°,AB=5,BC=3,则cos A的值是( )
A. B. . D.
2.如图,一艘船向东航行,上午8时到达A处,测得一灯塔B在船的北偏东30°方向,且距离船48 n mile;上午11时到达C处,测得灯塔在船的正北方向,则这艘船航行的速度为( )
A.24 n mile/h B.8n mile/h
C.24 n mile/h D.8 n mile/h
INCLUDEPICTURE"M19.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M19.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M19.tif" \* MERGEFORMATINET INCLUDEPICTURE"M20.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M20.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M20.tif" \* MERGEFORMATINET INCLUDEPICTURE"M21.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M21.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M21.tif" \* MERGEFORMATINET
(第2题) (第5题) (第7题)
3.点M(-sin 60°,cos 60°)关于x轴对称的点的坐标是( )
A. B. C. D.
4.在△ABC中,AB=12,AC=13,cos B=,则BC=( )
A.7 B.8 C.8或17 D.7或17
5. 如图是我们经常看到的一种折叠桌子的示意图,它是由下面的支架AD,BC与桌面构成的,已知OA=OB=OC=OD=20 cm,∠COD=60°,则点A到地面(CD所在的平面)的距离是( )
A.30 cm B.60 cm C.40 cm D.60 cm
6.已知等腰三角形ABC中,AB=AC=,底角为30°,动点P从点B向点C运动,当运动到PA与一腰垂直时BP长为( )
A.1 B.1或3 C.1或2 D.
7.如图,某梯子长10 m,斜靠在竖直的墙面上,当梯子与水平地面所成角为α时,梯子顶端靠在墙面上的点A处,底端落在水平地面的点B处,现将梯子底端向墙面靠近,使梯子与地面所成角为β,已知sin α=cos β=,则梯子顶端上升了( )
A.1 m B.1.5 m
C.2 m D.2.5 m
8.如图,在Rt△ABC中,∠C=90°,AC=3 cm,BC=4 cm,D从A出发沿AC方向以1 cm/s向终点C匀速运动,过点D作DE∥AB交BC于点E,过点E作EF⊥BC交AB于点F,当四边形ADEF为菱形时,点D运动的时间为( )
A. s B. s C. s D. s
INCLUDEPICTURE"M22.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M22.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M22.tif" \* MERGEFORMATINET INCLUDEPICTURE"M23.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M23.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M23.tif" \* MERGEFORMATINET INCLUDEPICTURE"M24.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M24.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M24.tif" \* MERGEFORMATINET
(第8题) (第10题) (第11题)
二、填空题(每题3分,共18分)
9.求值:sin 60°-tan 30°=________.
10.把一块直尺与一块三角尺按如图所示方式放置,若sin∠1=,则∠2的度数为________.
11.如图,一根竖直的木杆在离地面3.1 m处折断,木杆顶端落在地面上,且与地面成38°角,则木杆折断之前高度约为______m.(参考数据:sin 38°≈0.62,cos 38°≈0.79,tan 38°≈0.78)
12.如图,一束光线照在坡度为1∶ 的斜坡上,被斜坡上的平面镜反射成与地面平行的光线,则这束光线与坡面的夹角α是________度.
INCLUDEPICTURE"HS30.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\HS30.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\HS30.tif" \* MERGEFORMATINET INCLUDEPICTURE"M25.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M25.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M25.tif" \* MERGEFORMATINET INCLUDEPICTURE"J30.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\J30.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\J30.tif" \* MERGEFORMATINET
(第12题) (第13题) (第14题)
13.如图,Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,若AD=BC,则cos B=______.
14.如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点,当△APB为直角三角形时,AP=______________.
三、解答题(15题8分 ,16~20题每题10分,共58分)
15. 计算:
(1)4sin 30°-cos 45°-tan 30°+2sin 60°;
(2).
16. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,∠A=30°,BC=2.
INCLUDEPICTURE"M26.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M26.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M26.tif" \* MERGEFORMATINET
(第16题)
(1)求AB的长度;
(2)求△ABC的面积;
(3)求CD的长度.
17. 小明想测量一棵树AB的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长BF为8 m,坡面上的影长CF为4 m.已知斜坡的坡角为30°,同一时刻,一根长为1 m且垂直于地面放置的标杆在地面上的影长为2 m,求树AB的高度.
INCLUDEPICTURE"二改+43.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\二改+43.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\二改+43.tif" \* MERGEFORMATINET
(第17题)
18. 如图,为测量某观光塔的高度,一人先在附近一楼房的底端点A处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端点B处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45 m,求观光塔的高CD是多少米.
INCLUDEPICTURE"M27.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M27.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M27.tif" \* MERGEFORMATINET
(第18题)
19. 定义:在△ABC中,我们把∠A的对边与∠C 的对边的比叫做∠A的邻弦,记作thi A,即thi A==.请解答下列问题:
已知在△ABC中,∠C=30°.
(1)若∠A=45°,求thi A的值;
(2)若thi A= ,则∠A=________;
(3)若∠A是锐角,探究thi A与sin A的数量关系.
20.如图,在四边形ABCD中,AB∥DC,AB≠CD,∠BCD=90°,且AB=1,BC=2,tan ∠ADC=2.
(1)求证:DC=BC;
(2)E是四边形ABCD内一点,F是四边形ABCD外一点,且∠EDC=∠FBC,DE=BF,试判断△ECF的形状,并证明你的结论;
(3)在(2)的条件下,当BE∶CE=1∶2,∠BEC=135°时,求sin ∠BFE.
INCLUDEPICTURE"HS39.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\HS39.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\HS39.tif" \* MERGEFORMATINET
(第20题)
答案
一、1.D 2.D 3.B 4.D 5.D 6.C 7.C
8.D 点拨:设经过t s后,四边形ADEF是菱形,
∴AD=DE=t cm,DE∥AB,
∴CD=(3-t)cm,∠ABC=∠DEC,
∵∠C=90°,AC=3 cm,BC=4 cm,
∴AB===5(cm).
∵sin∠DEC=sin∠ABC==,
∴=,∴t=.
二、9. 10.135° 11.8.1 12.30
13. 点拨:设AD=BC=x,∵∠ACB=90°,CD⊥AB,
∴∠A+∠ACD=∠ACD+∠BCD=90°,∴∠A=∠BCD.又∠B=∠B,∴△ABC ∽△CBD,∴=,即=,∴BD=x(负根已经舍弃),∴cos B==.
14.3或3或3 点拨:当∠APB=90°时,分两种情况讨论.情况一:如图①,∵O是AB的中点,∠APB=90°,∴PO=BO=AO,∵∠1=120°,∴∠AOP=60°,∴△AOP为等边三角形,∴AP=OA=AB=3;情况二:如图②,∵O是AB的中点,∠APB=90°,∴PO=BO,∵∠1=120°,∴∠BOP=60°,∴△BOP为等边三角形,∴∠OBP=60°,∴AP=AB·sin 60°=6×=3;当∠BAP=90°时,如图③,∵O是AB的中点,∴OA=OB=AB=3.∵∠1=120°,∴∠AOP=60°,∴AP=OA·tan∠AOP=3×=3;当∠ABP=90°时,如图④,∵∠1=120°,∴∠BOP=60°.∵O是AB的中点,∴OB=AB=3,∴PB=OB·tan∠BOP=3×=3,
∴PA==3,故答案为3或3或3.
INCLUDEPICTURE"DA24-2.tif" INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\DA24-2.tif" \* MERGEFORMATINET (第14题)
三、15.解:(1)原式=4×-×-×+2×=2-1-1+=.
(2)原式===3-2.
16.解:(1)∵∠ACB=90°,∠A=30°,∴AB=2BC=4.
(2)在Rt△ABC中,∠ACB=90°,AB=4,BC=2,
根据勾股定理,得AC===2,
∴S△ABC=×BC×AC=×2×2=2.
(3)∵S△ABC=×AB×CD=2,AB=4,
∴×4×CD=2,解得CD=.
17.解:延长AC交BF延长线于点D,作CE⊥BD于点E,
在Rt△CFE中,∠CFE=30°,CF=4 m,∴CE=2 m,EF=4cos 30°=4×=2(m).
∵同一时刻,一根长为1 m且垂直于地面放置的标杆在地面上的影长为2 m,∴CE∶DE=1∶2,AB∶BD=1∶2,
∴DE=4 m,∴BD=BF+EF+ED=(12+2)m,
∴AB=BD=(12+2)=+6(m).
答:树AB的高度为(+6)m.
18.解:由题意得∠ADB=30°,∠CAD=60°,
在Rt△ABD中,AD==45 m.
在Rt△ACD中,CD=AD·tan 60°=45×=135(m).
答:观光塔的高CD是135 m.
19.解:(1)如图,在△ABC中,∠C=30°,∠A=45°.
作BH⊥AC,垂足为H.在Rt△BHC中,sin C==,
即BC=2BH.
在Rt△BHA中,sin A==,
INCLUDEPICTURE"DA24-6.tif" INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\DA24-6.tif" \* MERGEFORMATINET
(第19题)
即AB=BH.∴thi A==.
(2)60°或120°
(3)如图,在△ABC中,
∠C=30°,thi A=.
在Rt△BHA中,sin A=.在Rt△BHC中,sin C==,即BC=2BH.∴thi A=,即thi A=2sinA.
20.(1)证明:如图,过点A作DC的垂线AM,交DC于点M,∵AB∥DC,∠BCD=90°,∴∠ABC=90°,
易知四边形ABCM为矩形,∴AM=BC=2,MC=AB=1.
∵tan ∠ADC==2,∴DM=AM=1.
∴DC=DM+MC=2,∴DC=BC.
INCLUDEPICTURE"HS66.tif" INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\HS66.tif" \* MERGEFORMATINET
(第20题)
(2)解:△ECF是等腰直角三角形.
证明:如图,∵DE=BF,∠EDC=∠FBC,DC=BC,
∴△DEC ≌△BFC,∴∠1=∠3,EC=FC.
∴∠3+∠2=∠1+∠2=90°.
∴△ECF为等腰直角三角形.
(3)解:在(2)的条件下,∠CEF=45°,
∵∠BEC=135°,∴∠BEF=135°-45°=90°.
∵BE∶CE=1∶2,∴设BE=k,CE=2k,易知EF=2k,∴BF===3k.
在Rt△BEF中,sin ∠BFE===.
PAGE
