华东师大版九年级数学上册期末达标检测卷(Word版,附答案)
文档属性
| 名称 | 华东师大版九年级数学上册期末达标检测卷(Word版,附答案) |  | |
| 格式 | doc | ||
| 文件大小 | 284.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-03 23:07:23 | ||
图片预览




文档简介
华东师大版九年级数学上册 期末达标检测卷
(限时: 120分钟 满分: 100分)
班级: 姓名: 得分:
一、选择题(每题3分,共30分)
1.若 是最简二次根式,则a的值可能是( )
A.-2 B.2 C. D.8
2.某航空公司有若干个飞机场,每两个飞机场之间都开辟1条航线,一共开辟了10条航线,则这个航空公司共有飞机场( )
A.4个 B.5个 C.6个 D.7个
3.从如图所示的扑克牌中任取一张,牌面数字是3的倍数的概率是( )
A. B. C. D.
INCLUDEPICTURE"M33.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M33.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M33.tif" \* MERGEFORMATINET INCLUDEPICTURE"M35.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M35.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M35.tif" \* MERGEFORMATINET
(第3题) (第7题)
4.下列计算正确的是( )
A.-= B.=1
C.(2)2=24 D.3×2=6
5.用公式法解方程x2+4x=2,其中求得b2-4ac的值是( )
A.16 B.±4 C.32 D.64
6.在Rt△ABC中,∠C=90°,∠A=30°,AB+BC=12 cm,则AB等于( )
A.6 cm B.7 cm
C.8 cm D.9 cm
7.按如图所示的运算程序,能使输出的y值为的是( )
A.α=60°,β=45° B.α=30°,β=45°
C.α=30°,β=30° D.α=45°,β=30°
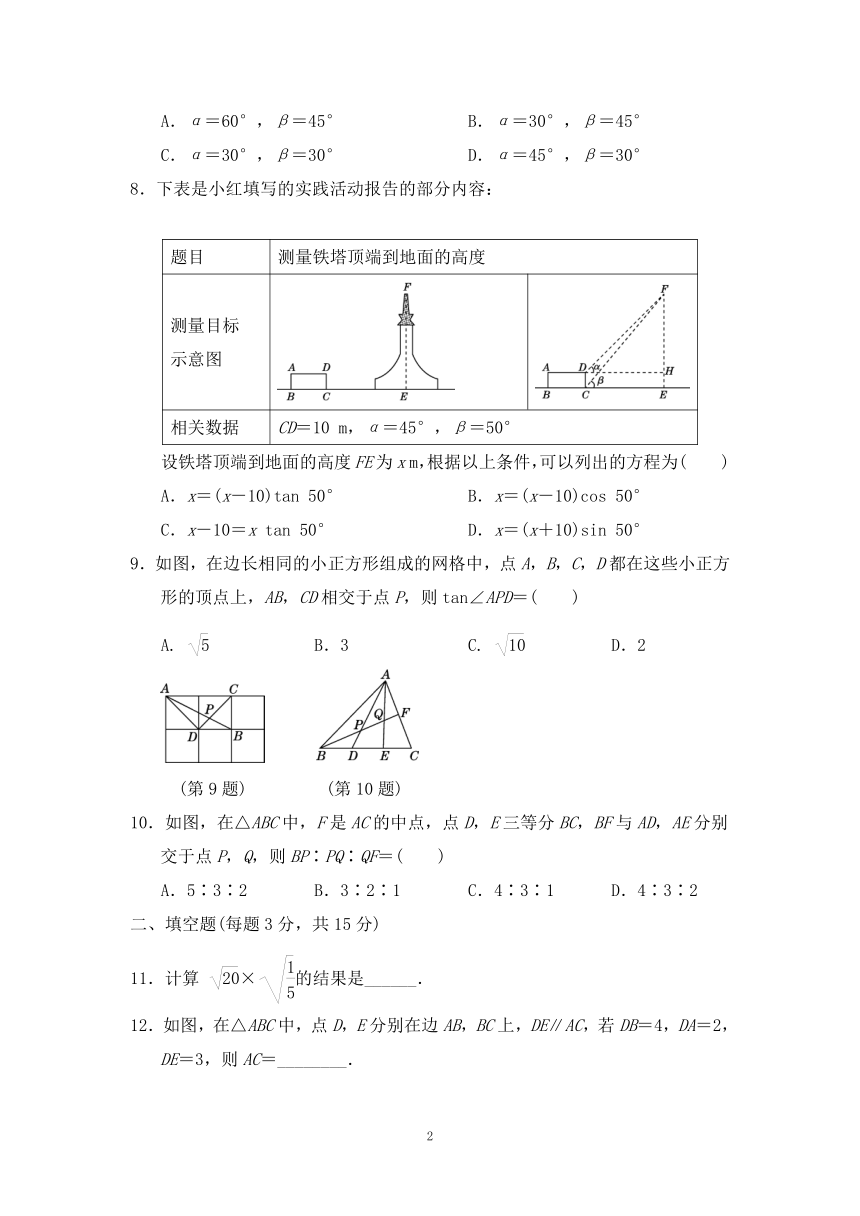
8.下表是小红填写的实践活动报告的部分内容:
题目 测量铁塔顶端到地面的高度
测量目标示意图 INCLUDEPICTURE"加227.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\加227.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\加227.tif" \* MERGEFORMATINET INCLUDEPICTURE"加228.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\加228.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\加228.tif" \* MERGEFORMATINET
相关数据 CD=10 m,α=45°,β=50°
设铁塔顶端到地面的高度FE为x m,根据以上条件,可以列出的方程为( )
A.x=(x-10)tan 50° B.x=(x-10)cos 50°
C.x-10=x tan 50° D.x=(x+10)sin 50°
9.如图,在边长相同的小正方形组成的网格中,点A,B,C,D都在这些小正方形的顶点上,AB,CD相交于点P,则tan∠APD=( )
A. B.3 C. D.2
INCLUDEPICTURE"M36.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M36.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M36.tif" \* MERGEFORMATINET INCLUDEPICTURE"M37.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M37.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M37.tif" \* MERGEFORMATINET
(第9题) (第10题)
10.如图,在△ABC中,F是AC的中点,点D,E三等分BC,BF与AD,AE分别交于点P,Q,则BP∶PQ∶QF=( )
A.5∶3∶2 B.3∶2∶1 C.4∶3∶1 D.4∶3∶2
二、填空题(每题3分,共15分)
11.计算×的结果是______.
12.如图,在△ABC中,点D,E分别在边AB,BC上,DE∥AC,若DB=4,DA=2,DE=3,则AC=________.
INCLUDEPICTURE"J41.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\J41.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\J41.tif" \* MERGEFORMATINET
(第12题)
13.已知x=m是关于x的一元二次方程x2+3x-1=0的根,则-=________.
14.如图,在Rt△ABC中,∠BAC=90°,AB=3,BC=5,点D是线段BC上一动点,连结AD,以AD为边作△ADE,使△ADE∽△ABC,则△ADE的最小面积与最大面积之比等于________.
INCLUDEPICTURE"加229.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\加229.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\加229.tif" \* MERGEFORMATINET
(第14题)
15.在△ABC中,∠ABC=30°,AB=4,AC=,则BC的长为________________.
三、解答题(16~18题每题8分,19~20题每题9分,21~22题每题10分,23题13分,共75分)
16. (1)计算:|1-|-+(π-3)0+;
(2)用公式法解方程:4x2+x-3=0.
17. 如图,在△ABC中,D是BC上的一点,E,F,G,H分别是BD,BC,AC,AD的中点,求证:EG,HF互相平分.
INCLUDEPICTURE"J42.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\J42.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\J42.tif" \* MERGEFORMATINET
(第17题)
18. 已知关于x的一元二次方程x2+(m+4)x-2m-12=0.
(1)求证:方程总有两个实数根;
(2)如果方程的两根相等,求此时方程的根.
19.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)以原点O为位似中心,相似比为2,在y轴的左侧,画出△ABC放大后的图形△A1B1C1;
(2)点C1的坐标为 ________;若线段AB上点D的坐标为(a,b),则对应的点D1的坐标为 ________;
(3)△A1B1C1的面积为________.
INCLUDEPICTURE"M38.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M38.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M38.tif" \* MERGEFORMATINET
(第19题)
20. 如图,有一个可自由转动的转盘,被分成了三个大小相同的扇形,分别标有数字2,4,6;另有一个不透明的瓶子,装有分别标有数字1,3,5的三个完全相同(除数字外)的小球,小杰先转动一次转盘,停止后记下指针指向的数字(若指针指在分界线上则重转),小玉再从瓶子中随机取出一个小球,记下小球上的数字.
(1)请用列表或画树状图的方法(选其中一种)表示出所有可能出现的结果;
INCLUDEPICTURE"1-50.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\1-50.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\1-50.tif" \* MERGEFORMATINET
(第20题)
(2)若得到的两数字之和为3的倍数,则小杰赢;若得到的两数字之和为7的倍数,则小玉赢,此游戏公平吗?为什么?
21. 周末,小涛想用所学的数学知识测量一斜坡上松树AB的高度(松树与地面垂直),测量时,他先选择在水平地面CD上的F处垂直于地面放置测角仪EF.从点E测得松树顶端A的仰角为45°,松树底部B的仰角为20°,已知斜坡上松树底部B到坡底C的距离BC=6 m,CF=1 m,坡角∠BCD=30°,测量示意图如图所示,请根据相关测量信息,求松树AB的高度.(参考数据:sin 20°≈0.34,cos 20°≈0.94,tan 20°≈0.36)
INCLUDEPICTURE"加230.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\加230.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\加230.tif" \* MERGEFORMATINET
(第21题)
22. 某淘宝网店销售台灯,每个台灯售价为60元,每星期可卖出300个,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30个.已知该款台灯每个成本为40元.
(1)若每个台灯降x元(x>0),则每星期能卖出________个台灯,每个台灯的利润是________元.
(2)在顾客得到实惠的前提下,该淘宝网店还想获得每星期6 480元的利润,那么应将每个台灯的售价定为多少元?
23. 在四边形ABCD的边AB上任取一点E(点E不与A,B重合),分别连结ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相似点”.
(1)如图①,∠A=∠B=∠DEC=45°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图②,在矩形ABCD中,A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点;
(3)如图③,将矩形ABCD沿CM折叠,使点D落在边AB上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB与BC的数量关系.
INCLUDEPICTURE"J45.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\J45.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\J45.tif" \* MERGEFORMATINET
(第23题)
答案
一、1.B 2.B 3.A 4.D 5.D 6.C 7.C 8.A
9.B 点拨:设小正方形的边长为1,
由题图可知AD=DC=,AC=2,∵AD2+DC2=AC2,
∴△ADC是等腰直角三角形,∴AD⊥DC.
∵AC∥BD,∴△ACP∽△BDP,∴==2,∴PC=2DP,
∴AD=DC=3DP,∴tan∠APD==3.
10.A 点拨:过点F作FN∥BC,交AE于点M,交AD于点N,如图.
INCLUDEPICTURE"b35.tif" INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\b35.tif" \* MERGEFORMATINET
(第10题)
∵F是AC的中点,∴易得FM是△AEC的中位线,∴CE=2FM.由题意得BD=DE=CE,∴BE=2CE=4FM.∵FM∥BC,∴△FMQ ∽△BEQ,∴==.易知FN是△ADC的中位线,∴FN=CD=CE=BD,
∵FN∥BC,∴△FNP ∽△BDP,∴==1,∴BP=PF=BF,∵=,∴=,∴FQ=BF,
∴PQ=PF-QF=BF-BF=BF,∴BP?PQ?QF=??=5∶3∶2.
二、11.2 12. 13.-4
14. 点拨:∵在Rt△ABC中,∠BAC=90°,AB=3,
BC=5,∴AC=4.当AD⊥BC时,△ADE的面积最小,
易得此时AD===.
∵△ADE ∽△ABC,∴=,∴=,
∴AE=,∴△ADE的最小面积为××=;
当D与C重合,即AD=4时,△ADE的面积最大.
∵=,
∴=,∴AE=,
∴△ADE的最大面积为×4×=.
∴△ADE的最小面积与最大面积之比为=.
15.5或7
三、16.解:(1)原式=-1-2+1+3=-+3.
(2)∵a=4,b=1,c=-3,∴Δ=12-4×4×(-3)=49,
∴x=,∴x1=-1,x2=.
17.证明:连结EH,GH,GF.
∵E,F,G,H分别是BD,BC,AC,AD的中点,∴AB∥EH∥GF,GH∥EF,∴四边形EHGF为平行四边形.
∵EG,HF为 EHGF的对角线,
∴EG,HF互相平分.
18.(1)证明:∵Δ=(m+4)2-4(-2m-12)=m2+16m+64=(m+8)2≥0,∴方程总有两个实数根.
(2)解:如果方程的两根相等,
则Δ=(m+8)2=0,解得m=-8,
此时方程为x2-4x+4=0,
即(x-2)2=0,解得x1=x2=2.
19.解:(1)如图,△A1B1C1即为所作.
INCLUDEPICTURE"b37.tif" INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\b37.tif" \* MERGEFORMATINET (第19题)
(2)(-6,4);(2a,2b) (3)8
20.解:(1)用列表法表示所有可能出现的结果如下:
转盘摸球 2 4 6
1 (2,1) (4,1) (6,1)
3 (2,3) (4,3) (6,3)
5 (2,5) (4,5) (6,5)
共有9种不同结果,即(2,1),(2,3),(2,5),(4,1),(4,3),(4,5),(6,1),(6,3),(6,5).
(2)公平.理由如下:列出两数字之和的所有可能的结果如下:
转盘摸球 2 4 6
1 2+1=3 4+1=5 6+1=7
3 2+3=5 4+3=7 6+3=9
5 2+5=7 4+5=9 6+5=11
共有9种等可能出现的结果,其中“和为3的倍数”的有3种,“和为7的倍数”的有3种,所以P(小杰赢)==,P(小玉赢)==,因此游戏是公平的.
21.解:如图,延长AB交CD于点M,过点E作EG⊥AM,垂足为G.由题意得AM⊥CD.
∵松树底部B到坡底C的距离BC=6m,斜坡的坡角为30°,∴在Rt△BMC中,MC=BC·cos 30°=6×=9(m).∵CF=1 m,∴MF=9+1=10(m),
∴易得GE=10 m.∵∠AEG=45°,∴AG=EG=10 m.
在Rt△BGE中,BG=GE·tan 20°≈10×0.36=3.6(m),∴AB=AG-BG≈10-3.6=6.4(m).
答:松树AB的高度约为6.4 m.
INCLUDEPICTURE"加237.tif" INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\加237.tif" \* MERGEFORMATINET INCLUDEPICTURE"QM-4.tif" INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\QM-4.tif" \* MERGEFORMATINET
(第21题) (第23题)
22.解:(1)(300+30x);(20-x)
(2)由题意,得(20-x)(300+30x)=6 480,
解得x1=8,x2=2(舍去).60-8=52(元).
答:应将每个台灯的售价定为52元.
23.解:(1)是.理由:∵∠A=∠B=∠DEC=45°,
∴∠AED+∠ADE=135°,∠AED+∠CEB=135°,
∴∠ADE=∠CEB.在△ADE和△BEC中,∠A=∠B,∠ADE=∠BEC,∴△ADE ∽△BEC,
∴点E是四边形ABCD的边AB上的相似点.
(2)如图,E1和E2均是矩形ABCD的边AB上的强相似点.
(3)∵点E是四边形ABCM的边AB上的一个强相似点,∴△AEM ∽△BCE ∽△ECM.∴∠BCE=∠ECM.
由折叠可知△ECM ≌△DCM,∴∠ECM=∠DCM =∠BCE,CE=CD=AB,∴∠BCE=∠BCD=×90°=30°,∴在Rt△BCE中,cos∠BCE==cos 30°=,∴=.
PAGE
(限时: 120分钟 满分: 100分)
班级: 姓名: 得分:
一、选择题(每题3分,共30分)
1.若 是最简二次根式,则a的值可能是( )
A.-2 B.2 C. D.8
2.某航空公司有若干个飞机场,每两个飞机场之间都开辟1条航线,一共开辟了10条航线,则这个航空公司共有飞机场( )
A.4个 B.5个 C.6个 D.7个
3.从如图所示的扑克牌中任取一张,牌面数字是3的倍数的概率是( )
A. B. C. D.
INCLUDEPICTURE"M33.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M33.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M33.tif" \* MERGEFORMATINET INCLUDEPICTURE"M35.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M35.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M35.tif" \* MERGEFORMATINET
(第3题) (第7题)
4.下列计算正确的是( )
A.-= B.=1
C.(2)2=24 D.3×2=6
5.用公式法解方程x2+4x=2,其中求得b2-4ac的值是( )
A.16 B.±4 C.32 D.64
6.在Rt△ABC中,∠C=90°,∠A=30°,AB+BC=12 cm,则AB等于( )
A.6 cm B.7 cm
C.8 cm D.9 cm
7.按如图所示的运算程序,能使输出的y值为的是( )
A.α=60°,β=45° B.α=30°,β=45°
C.α=30°,β=30° D.α=45°,β=30°
8.下表是小红填写的实践活动报告的部分内容:
题目 测量铁塔顶端到地面的高度
测量目标示意图 INCLUDEPICTURE"加227.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\加227.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\加227.tif" \* MERGEFORMATINET INCLUDEPICTURE"加228.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\加228.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\加228.tif" \* MERGEFORMATINET
相关数据 CD=10 m,α=45°,β=50°
设铁塔顶端到地面的高度FE为x m,根据以上条件,可以列出的方程为( )
A.x=(x-10)tan 50° B.x=(x-10)cos 50°
C.x-10=x tan 50° D.x=(x+10)sin 50°
9.如图,在边长相同的小正方形组成的网格中,点A,B,C,D都在这些小正方形的顶点上,AB,CD相交于点P,则tan∠APD=( )
A. B.3 C. D.2
INCLUDEPICTURE"M36.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M36.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M36.tif" \* MERGEFORMATINET INCLUDEPICTURE"M37.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M37.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M37.tif" \* MERGEFORMATINET
(第9题) (第10题)
10.如图,在△ABC中,F是AC的中点,点D,E三等分BC,BF与AD,AE分别交于点P,Q,则BP∶PQ∶QF=( )
A.5∶3∶2 B.3∶2∶1 C.4∶3∶1 D.4∶3∶2
二、填空题(每题3分,共15分)
11.计算×的结果是______.
12.如图,在△ABC中,点D,E分别在边AB,BC上,DE∥AC,若DB=4,DA=2,DE=3,则AC=________.
INCLUDEPICTURE"J41.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\J41.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\J41.tif" \* MERGEFORMATINET
(第12题)
13.已知x=m是关于x的一元二次方程x2+3x-1=0的根,则-=________.
14.如图,在Rt△ABC中,∠BAC=90°,AB=3,BC=5,点D是线段BC上一动点,连结AD,以AD为边作△ADE,使△ADE∽△ABC,则△ADE的最小面积与最大面积之比等于________.
INCLUDEPICTURE"加229.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\加229.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\加229.tif" \* MERGEFORMATINET
(第14题)
15.在△ABC中,∠ABC=30°,AB=4,AC=,则BC的长为________________.
三、解答题(16~18题每题8分,19~20题每题9分,21~22题每题10分,23题13分,共75分)
16. (1)计算:|1-|-+(π-3)0+;
(2)用公式法解方程:4x2+x-3=0.
17. 如图,在△ABC中,D是BC上的一点,E,F,G,H分别是BD,BC,AC,AD的中点,求证:EG,HF互相平分.
INCLUDEPICTURE"J42.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\J42.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\J42.tif" \* MERGEFORMATINET
(第17题)
18. 已知关于x的一元二次方程x2+(m+4)x-2m-12=0.
(1)求证:方程总有两个实数根;
(2)如果方程的两根相等,求此时方程的根.
19.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)以原点O为位似中心,相似比为2,在y轴的左侧,画出△ABC放大后的图形△A1B1C1;
(2)点C1的坐标为 ________;若线段AB上点D的坐标为(a,b),则对应的点D1的坐标为 ________;
(3)△A1B1C1的面积为________.
INCLUDEPICTURE"M38.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\M38.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\M38.tif" \* MERGEFORMATINET
(第19题)
20. 如图,有一个可自由转动的转盘,被分成了三个大小相同的扇形,分别标有数字2,4,6;另有一个不透明的瓶子,装有分别标有数字1,3,5的三个完全相同(除数字外)的小球,小杰先转动一次转盘,停止后记下指针指向的数字(若指针指在分界线上则重转),小玉再从瓶子中随机取出一个小球,记下小球上的数字.
(1)请用列表或画树状图的方法(选其中一种)表示出所有可能出现的结果;
INCLUDEPICTURE"1-50.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\1-50.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\1-50.tif" \* MERGEFORMATINET
(第20题)
(2)若得到的两数字之和为3的倍数,则小杰赢;若得到的两数字之和为7的倍数,则小玉赢,此游戏公平吗?为什么?
21. 周末,小涛想用所学的数学知识测量一斜坡上松树AB的高度(松树与地面垂直),测量时,他先选择在水平地面CD上的F处垂直于地面放置测角仪EF.从点E测得松树顶端A的仰角为45°,松树底部B的仰角为20°,已知斜坡上松树底部B到坡底C的距离BC=6 m,CF=1 m,坡角∠BCD=30°,测量示意图如图所示,请根据相关测量信息,求松树AB的高度.(参考数据:sin 20°≈0.34,cos 20°≈0.94,tan 20°≈0.36)
INCLUDEPICTURE"加230.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\加230.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\加230.tif" \* MERGEFORMATINET
(第21题)
22. 某淘宝网店销售台灯,每个台灯售价为60元,每星期可卖出300个,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30个.已知该款台灯每个成本为40元.
(1)若每个台灯降x元(x>0),则每星期能卖出________个台灯,每个台灯的利润是________元.
(2)在顾客得到实惠的前提下,该淘宝网店还想获得每星期6 480元的利润,那么应将每个台灯的售价定为多少元?
23. 在四边形ABCD的边AB上任取一点E(点E不与A,B重合),分别连结ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相似点”.
(1)如图①,∠A=∠B=∠DEC=45°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图②,在矩形ABCD中,A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点;
(3)如图③,将矩形ABCD沿CM折叠,使点D落在边AB上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB与BC的数量关系.
INCLUDEPICTURE"J45.tif" INCLUDEPICTURE "D:\\方正转Word\\9HS全国\\J45.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\J45.tif" \* MERGEFORMATINET
(第23题)
答案
一、1.B 2.B 3.A 4.D 5.D 6.C 7.C 8.A
9.B 点拨:设小正方形的边长为1,
由题图可知AD=DC=,AC=2,∵AD2+DC2=AC2,
∴△ADC是等腰直角三角形,∴AD⊥DC.
∵AC∥BD,∴△ACP∽△BDP,∴==2,∴PC=2DP,
∴AD=DC=3DP,∴tan∠APD==3.
10.A 点拨:过点F作FN∥BC,交AE于点M,交AD于点N,如图.
INCLUDEPICTURE"b35.tif" INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\b35.tif" \* MERGEFORMATINET
(第10题)
∵F是AC的中点,∴易得FM是△AEC的中位线,∴CE=2FM.由题意得BD=DE=CE,∴BE=2CE=4FM.∵FM∥BC,∴△FMQ ∽△BEQ,∴==.易知FN是△ADC的中位线,∴FN=CD=CE=BD,
∵FN∥BC,∴△FNP ∽△BDP,∴==1,∴BP=PF=BF,∵=,∴=,∴FQ=BF,
∴PQ=PF-QF=BF-BF=BF,∴BP?PQ?QF=??=5∶3∶2.
二、11.2 12. 13.-4
14. 点拨:∵在Rt△ABC中,∠BAC=90°,AB=3,
BC=5,∴AC=4.当AD⊥BC时,△ADE的面积最小,
易得此时AD===.
∵△ADE ∽△ABC,∴=,∴=,
∴AE=,∴△ADE的最小面积为××=;
当D与C重合,即AD=4时,△ADE的面积最大.
∵=,
∴=,∴AE=,
∴△ADE的最大面积为×4×=.
∴△ADE的最小面积与最大面积之比为=.
15.5或7
三、16.解:(1)原式=-1-2+1+3=-+3.
(2)∵a=4,b=1,c=-3,∴Δ=12-4×4×(-3)=49,
∴x=,∴x1=-1,x2=.
17.证明:连结EH,GH,GF.
∵E,F,G,H分别是BD,BC,AC,AD的中点,∴AB∥EH∥GF,GH∥EF,∴四边形EHGF为平行四边形.
∵EG,HF为 EHGF的对角线,
∴EG,HF互相平分.
18.(1)证明:∵Δ=(m+4)2-4(-2m-12)=m2+16m+64=(m+8)2≥0,∴方程总有两个实数根.
(2)解:如果方程的两根相等,
则Δ=(m+8)2=0,解得m=-8,
此时方程为x2-4x+4=0,
即(x-2)2=0,解得x1=x2=2.
19.解:(1)如图,△A1B1C1即为所作.
INCLUDEPICTURE"b37.tif" INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\b37.tif" \* MERGEFORMATINET (第19题)
(2)(-6,4);(2a,2b) (3)8
20.解:(1)用列表法表示所有可能出现的结果如下:
转盘摸球 2 4 6
1 (2,1) (4,1) (6,1)
3 (2,3) (4,3) (6,3)
5 (2,5) (4,5) (6,5)
共有9种不同结果,即(2,1),(2,3),(2,5),(4,1),(4,3),(4,5),(6,1),(6,3),(6,5).
(2)公平.理由如下:列出两数字之和的所有可能的结果如下:
转盘摸球 2 4 6
1 2+1=3 4+1=5 6+1=7
3 2+3=5 4+3=7 6+3=9
5 2+5=7 4+5=9 6+5=11
共有9种等可能出现的结果,其中“和为3的倍数”的有3种,“和为7的倍数”的有3种,所以P(小杰赢)==,P(小玉赢)==,因此游戏是公平的.
21.解:如图,延长AB交CD于点M,过点E作EG⊥AM,垂足为G.由题意得AM⊥CD.
∵松树底部B到坡底C的距离BC=6m,斜坡的坡角为30°,∴在Rt△BMC中,MC=BC·cos 30°=6×=9(m).∵CF=1 m,∴MF=9+1=10(m),
∴易得GE=10 m.∵∠AEG=45°,∴AG=EG=10 m.
在Rt△BGE中,BG=GE·tan 20°≈10×0.36=3.6(m),∴AB=AG-BG≈10-3.6=6.4(m).
答:松树AB的高度约为6.4 m.
INCLUDEPICTURE"加237.tif" INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\加237.tif" \* MERGEFORMATINET INCLUDEPICTURE"QM-4.tif" INCLUDEPICTURE "F:\\22秋\\9数全国HS\\点训九数上HS文件\\QM-4.tif" \* MERGEFORMATINET
(第21题) (第23题)
22.解:(1)(300+30x);(20-x)
(2)由题意,得(20-x)(300+30x)=6 480,
解得x1=8,x2=2(舍去).60-8=52(元).
答:应将每个台灯的售价定为52元.
23.解:(1)是.理由:∵∠A=∠B=∠DEC=45°,
∴∠AED+∠ADE=135°,∠AED+∠CEB=135°,
∴∠ADE=∠CEB.在△ADE和△BEC中,∠A=∠B,∠ADE=∠BEC,∴△ADE ∽△BEC,
∴点E是四边形ABCD的边AB上的相似点.
(2)如图,E1和E2均是矩形ABCD的边AB上的强相似点.
(3)∵点E是四边形ABCM的边AB上的一个强相似点,∴△AEM ∽△BCE ∽△ECM.∴∠BCE=∠ECM.
由折叠可知△ECM ≌△DCM,∴∠ECM=∠DCM =∠BCE,CE=CD=AB,∴∠BCE=∠BCD=×90°=30°,∴在Rt△BCE中,cos∠BCE==cos 30°=,∴=.
PAGE
同课章节目录
