人教版七年级数学下册 5.2.2平行线的判定 课件(共23张PPT)
文档属性
| 名称 | 人教版七年级数学下册 5.2.2平行线的判定 课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-04 08:15:15 | ||
图片预览


文档简介
(共23张PPT)
5.2.2平行线的判定(1)
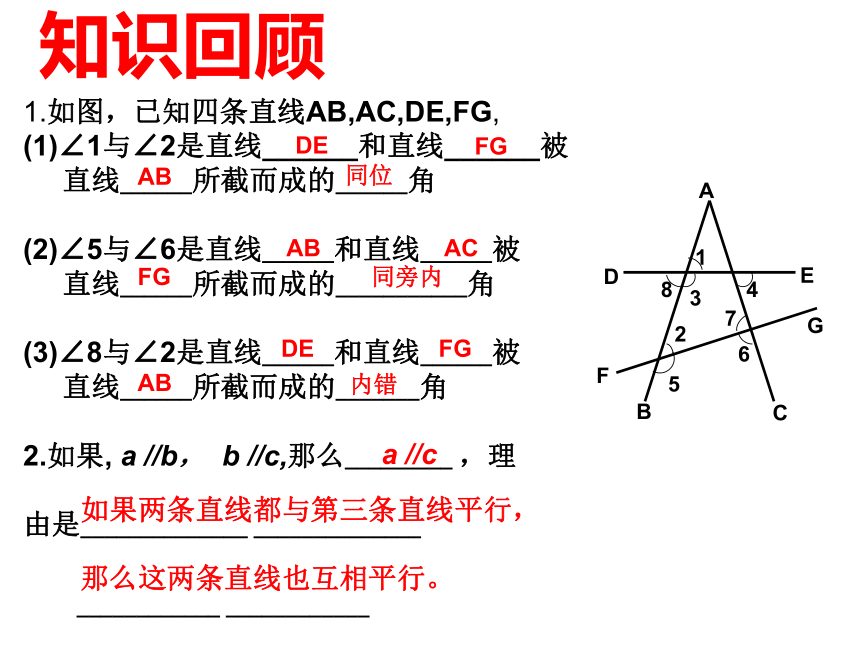
1.如图,已知四条直线AB,AC,DE,FG,
∠1与∠2是直线______和直线______被
直线______所截而成的______角
(2)∠5与∠6是直线______和直线______被
直线______所截而成的___________角
(3)∠8与∠2是直线______和直线______被
直线______所截而成的_______角
2.如果, a //b, b //c,那么_________ ,理
由是______________ ______________
____________ ____________
A
B
C
E
D
F
G
知识回顾
1
7
3
6
4
8
5
2
FG
DE
AB
同位
AC
AB
FG
同旁内
DE
FG
AB
内错
a //c
如果两条直线都与第三条直线平行,
那么这两条直线也互相平行。
注意观察!
a
b
.
A
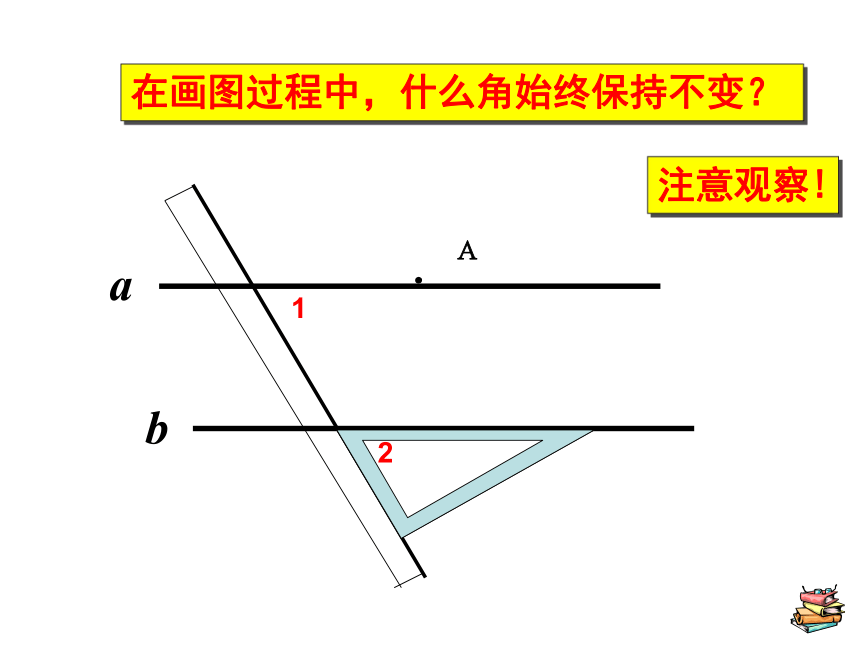
在画图过程中,什么角始终保持不变?
2
1
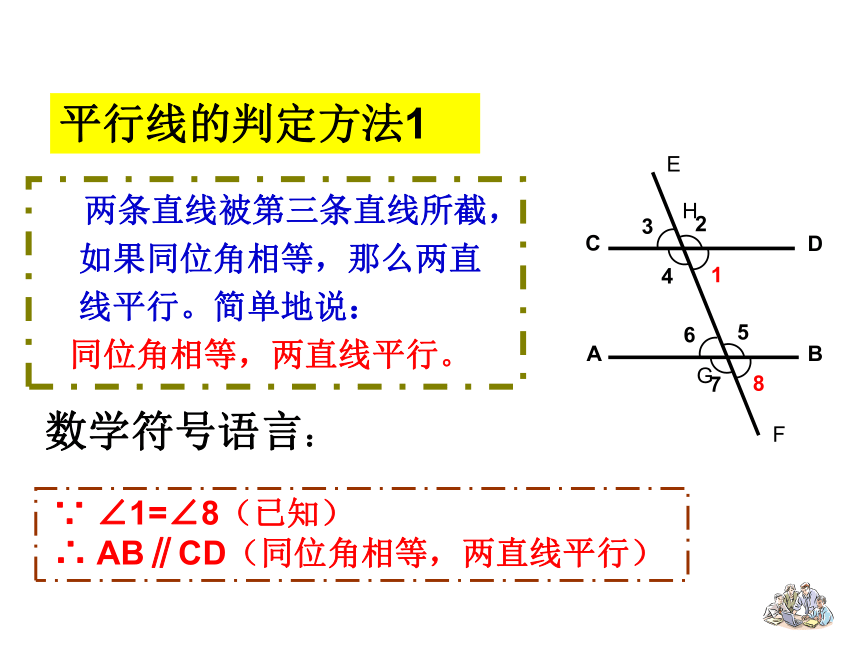
两条直线被第三条直线所截,如果同位角相等,那么两直线平行。简单地说:
同位角相等,两直线平行。
∵ ∠1=∠8(已知)
∴ AB∥CD(同位角相等,两直线平行)
数学符号语言:
C
A
2
1
3
4
5
8
6
7
D
B
平行线的判定方法1
E
F
H
G
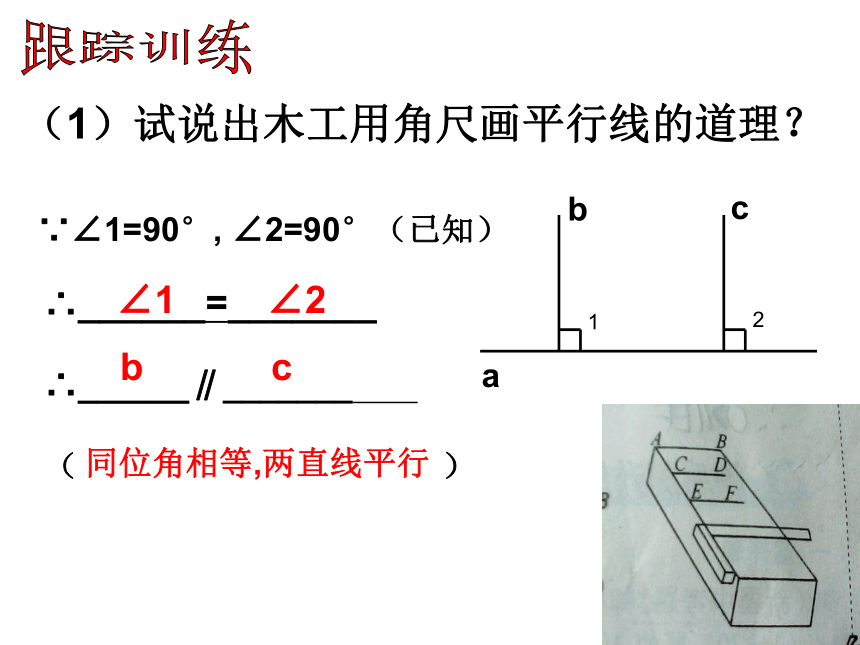
(1)试说出木工用角尺画平行线的道理?
∴______=_______
∴______∥_______
( )
1
2
a
c
b
b
c
同位角相等,两直线平行
∵∠1=90°, ∠2=90°(已知)
∠1
∠2
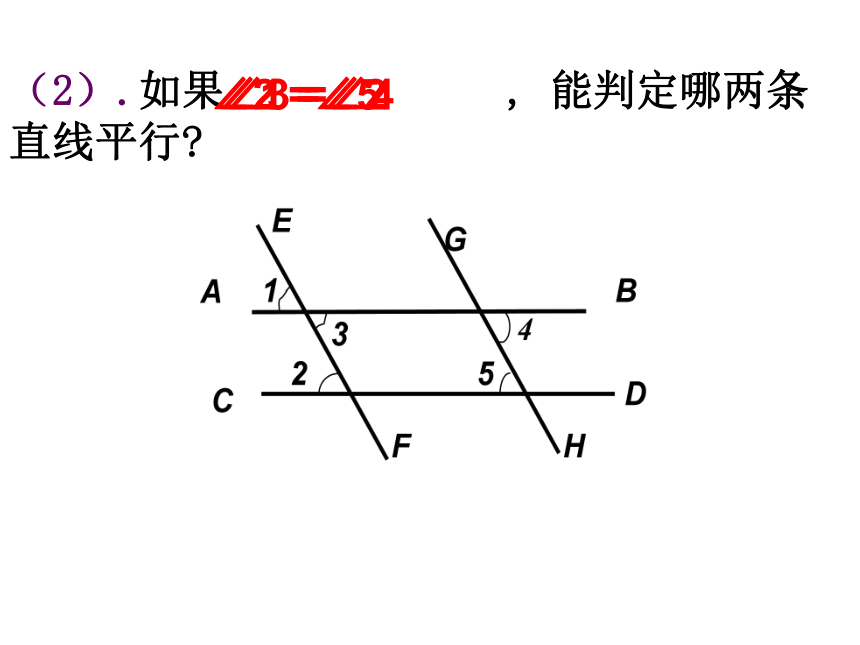
(2).如果 , 能判定哪两条直线平行
∠1 =∠2
∠2 =∠5
∠3 =∠4
D
A
B
E
1
3
4
2
F
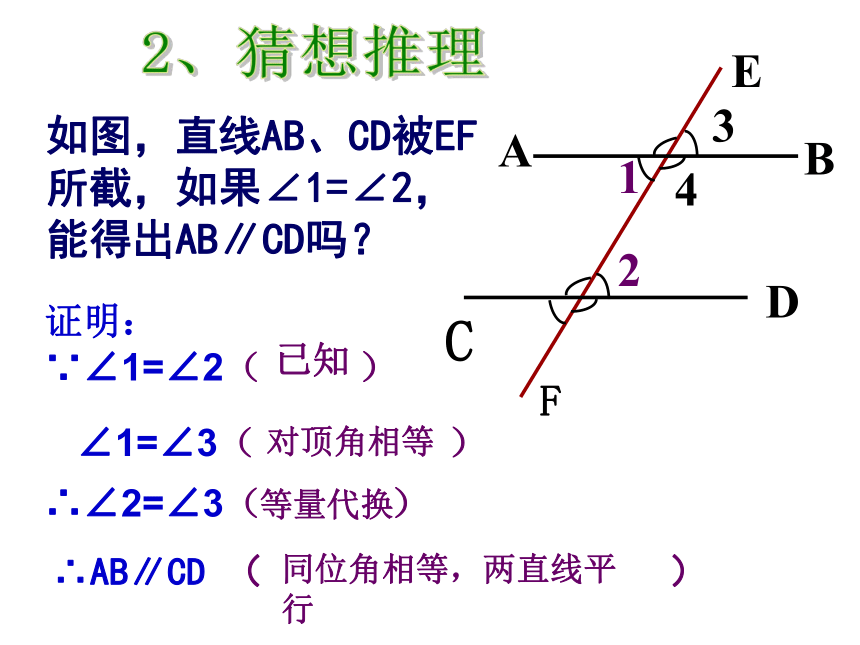
如图,直线AB、CD被EF所截,如果∠1=∠2,
能得出AB∥CD吗?
∴AB∥CD ( )
C
已知
对顶角相等
等量代换
同位角相等,两直线平行
证明:
∵∠1=∠2( )
∠1=∠3( )
∴∠2=∠3( )
平行线的判定方法2
两条直线被第三条直线所截,如果内错角相等,那么两条直线平行。
简单说成:内错角相等,两直线平行。
数学符号语言:
∵∠1=∠7 (已知)
∴AB∥CD(内错角相等,两直线平行)
D
A
B
E
8
5
6
1
2
3
4
7
C
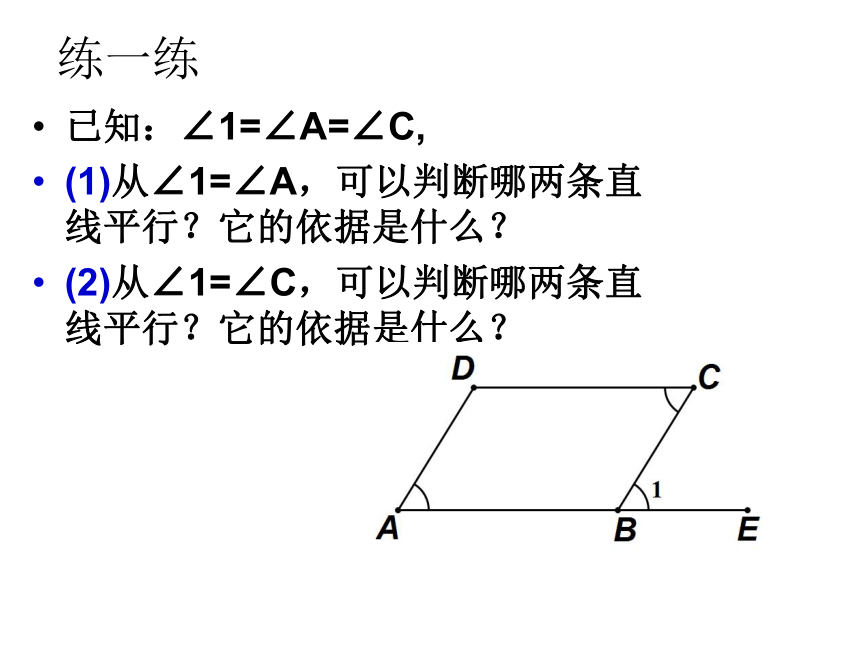
练一练
已知:∠1=∠A=∠C,
(1)从∠1=∠A,可以判断哪两条直线平行?它的依据是什么?
(2)从∠1=∠C,可以判断哪两条直线平行?它的依据是什么?
3、同旁内角数量上满足什么关系时,两直线平行?说明你的理由:
解:当) ∠2+∠4= 1800时 ,两直线平行。
∵∠1 +∠4= 180o ( )
∠2 +∠4= 180o ( )
∴∠1= ∠2 ( )
∴ a∥b ( )
a
b
1
4
3
2
c
或∵∠1 +∠4= 180o (已知)
∠3 +∠4= 180o (邻补角定义)
∴∠2= ∠3 (同角的补角相等 )
∴ a∥b(内错角相等,两直线平行)
邻补角定义
已知
同角的补角相等
同位角相等,两直线平行
数学符号语言:
∵∠2 +∠4= 180o (已知)
∴ a∥b(同旁内角互补两直线平行)
a
b
1
4
3
2
c
平行线的判定方法3
两条直线被第三条直线所截,如果同旁内角互补,那么两直线平行。
简单说成:同旁内角互补,两直线平行。
4、通 过 判 定 方 法 2 和 3 的 推 理 我 们 得 出,遇 到 一 个 新 问 题时,常 常 把 它 转 化 为__ 的 问题。
已知
b
c
a
1
2
5、自学14页例题,
在同一平面内,垂直于同一条直线的两条直线平行。
从而得出:
方法2 (内错角)
方法3(同旁内角)
方法1 (同位角)
还有其它证明方法吗?
答:这两条直线平行.
理由如下:
a
b
c
1
2
∵b⊥a ,c ⊥a (已知)
∴b∥c,(同位角相等,两直线平行)
∴∠1= ∠2 = 90°
(垂直的定义)
解法1:
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)
a
b
c
1
2
解法2:
答:这两条直线平行.
理由如下:
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)
a
b
c
1
2
解法3:
答:这两条直线平行.
理由如下:
同位角相等,两直线平行。
同旁内角互补,两直线平行。
平行线的定义:在同一平面内,不相交的两条直线平行。
平行公理的推论:平行于同一条直线的两条 直线平行。
内错角相等,两直线平行。
两直线平行的判定方法有哪些
在同一平面内,垂直于同一条直线的两
条直线平行。
练习1.
① ∵ ∠2 =___(已知)
∴ ___∥___( )
② ∵ ∠3 = ∠5(已知)
∴ ___∥___( )
③∵ ∠4 +___=180o(已知)
∴ ___∥___( )
∠6
AB
CD
AB
CD
∠5
AB
CD
A
C
1
4
2
3
5
8
6
7
B
D
如图:
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
平行线的判定
1
2
3
A
B
C
D
4
如图,如果 1= 4,那么AB
是否和CD平行,说明你的理由。
∴AB∥CD(同位角相等,两直线平行)
∵∠1=∠2(对顶角相等)
练习2.
∠1=∠4(已知)
∴ ∠2=∠4(等量代换)
解:这两条直线平行.
理由如下:
(1)如图1,∵∠1= ____
∴____∥____( )
b
2
3
a
c
d
1
4
5
图1
(2)如图2,∵∠A+ ______ = 180 (已知)
∴______∥______(
A
B
D
C
图2
2、(10分)
a
b
内错角相等,两直线平行
AB
CD
同旁内角互补,
两直线平行)
达标检测
1、填空(每空2分)
∠2
∠D
如图3,BC、DE分别平分 ABD和 BDF,
且 1= 2,请找出平行线,并说明理由。
图3
B
2
F
E
D
C
A
1
我们本节课用到了
“数形结合”、
“转化”的数学思想。
我们学习了两直线平行的判定方法及数学符号语言.
找到图形中的同位角、内错角或同旁内角。
不经历风雨,怎么见彩虹
没有人能随随便便成功!
5.2.2平行线的判定(1)
1.如图,已知四条直线AB,AC,DE,FG,
∠1与∠2是直线______和直线______被
直线______所截而成的______角
(2)∠5与∠6是直线______和直线______被
直线______所截而成的___________角
(3)∠8与∠2是直线______和直线______被
直线______所截而成的_______角
2.如果, a //b, b //c,那么_________ ,理
由是______________ ______________
____________ ____________
A
B
C
E
D
F
G
知识回顾
1
7
3
6
4
8
5
2
FG
DE
AB
同位
AC
AB
FG
同旁内
DE
FG
AB
内错
a //c
如果两条直线都与第三条直线平行,
那么这两条直线也互相平行。
注意观察!
a
b
.
A
在画图过程中,什么角始终保持不变?
2
1
两条直线被第三条直线所截,如果同位角相等,那么两直线平行。简单地说:
同位角相等,两直线平行。
∵ ∠1=∠8(已知)
∴ AB∥CD(同位角相等,两直线平行)
数学符号语言:
C
A
2
1
3
4
5
8
6
7
D
B
平行线的判定方法1
E
F
H
G
(1)试说出木工用角尺画平行线的道理?
∴______=_______
∴______∥_______
( )
1
2
a
c
b
b
c
同位角相等,两直线平行
∵∠1=90°, ∠2=90°(已知)
∠1
∠2
(2).如果 , 能判定哪两条直线平行
∠1 =∠2
∠2 =∠5
∠3 =∠4
D
A
B
E
1
3
4
2
F
如图,直线AB、CD被EF所截,如果∠1=∠2,
能得出AB∥CD吗?
∴AB∥CD ( )
C
已知
对顶角相等
等量代换
同位角相等,两直线平行
证明:
∵∠1=∠2( )
∠1=∠3( )
∴∠2=∠3( )
平行线的判定方法2
两条直线被第三条直线所截,如果内错角相等,那么两条直线平行。
简单说成:内错角相等,两直线平行。
数学符号语言:
∵∠1=∠7 (已知)
∴AB∥CD(内错角相等,两直线平行)
D
A
B
E
8
5
6
1
2
3
4
7
C
练一练
已知:∠1=∠A=∠C,
(1)从∠1=∠A,可以判断哪两条直线平行?它的依据是什么?
(2)从∠1=∠C,可以判断哪两条直线平行?它的依据是什么?
3、同旁内角数量上满足什么关系时,两直线平行?说明你的理由:
解:当) ∠2+∠4= 1800时 ,两直线平行。
∵∠1 +∠4= 180o ( )
∠2 +∠4= 180o ( )
∴∠1= ∠2 ( )
∴ a∥b ( )
a
b
1
4
3
2
c
或∵∠1 +∠4= 180o (已知)
∠3 +∠4= 180o (邻补角定义)
∴∠2= ∠3 (同角的补角相等 )
∴ a∥b(内错角相等,两直线平行)
邻补角定义
已知
同角的补角相等
同位角相等,两直线平行
数学符号语言:
∵∠2 +∠4= 180o (已知)
∴ a∥b(同旁内角互补两直线平行)
a
b
1
4
3
2
c
平行线的判定方法3
两条直线被第三条直线所截,如果同旁内角互补,那么两直线平行。
简单说成:同旁内角互补,两直线平行。
4、通 过 判 定 方 法 2 和 3 的 推 理 我 们 得 出,遇 到 一 个 新 问 题时,常 常 把 它 转 化 为__ 的 问题。
已知
b
c
a
1
2
5、自学14页例题,
在同一平面内,垂直于同一条直线的两条直线平行。
从而得出:
方法2 (内错角)
方法3(同旁内角)
方法1 (同位角)
还有其它证明方法吗?
答:这两条直线平行.
理由如下:
a
b
c
1
2
∵b⊥a ,c ⊥a (已知)
∴b∥c,(同位角相等,两直线平行)
∴∠1= ∠2 = 90°
(垂直的定义)
解法1:
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)
a
b
c
1
2
解法2:
答:这两条直线平行.
理由如下:
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)
a
b
c
1
2
解法3:
答:这两条直线平行.
理由如下:
同位角相等,两直线平行。
同旁内角互补,两直线平行。
平行线的定义:在同一平面内,不相交的两条直线平行。
平行公理的推论:平行于同一条直线的两条 直线平行。
内错角相等,两直线平行。
两直线平行的判定方法有哪些
在同一平面内,垂直于同一条直线的两
条直线平行。
练习1.
① ∵ ∠2 =___(已知)
∴ ___∥___( )
② ∵ ∠3 = ∠5(已知)
∴ ___∥___( )
③∵ ∠4 +___=180o(已知)
∴ ___∥___( )
∠6
AB
CD
AB
CD
∠5
AB
CD
A
C
1
4
2
3
5
8
6
7
B
D
如图:
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
平行线的判定
1
2
3
A
B
C
D
4
如图,如果 1= 4,那么AB
是否和CD平行,说明你的理由。
∴AB∥CD(同位角相等,两直线平行)
∵∠1=∠2(对顶角相等)
练习2.
∠1=∠4(已知)
∴ ∠2=∠4(等量代换)
解:这两条直线平行.
理由如下:
(1)如图1,∵∠1= ____
∴____∥____( )
b
2
3
a
c
d
1
4
5
图1
(2)如图2,∵∠A+ ______ = 180 (已知)
∴______∥______(
A
B
D
C
图2
2、(10分)
a
b
内错角相等,两直线平行
AB
CD
同旁内角互补,
两直线平行)
达标检测
1、填空(每空2分)
∠2
∠D
如图3,BC、DE分别平分 ABD和 BDF,
且 1= 2,请找出平行线,并说明理由。
图3
B
2
F
E
D
C
A
1
我们本节课用到了
“数形结合”、
“转化”的数学思想。
我们学习了两直线平行的判定方法及数学符号语言.
找到图形中的同位角、内错角或同旁内角。
不经历风雨,怎么见彩虹
没有人能随随便便成功!
