苏科版八年级数学下册 10.1 分式 课件(共27张PPT)
文档属性
| 名称 | 苏科版八年级数学下册 10.1 分式 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 438.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-04 08:20:01 | ||
图片预览







文档简介
(共27张PPT)
10.1 分式
早晨,我开车前往学校的途中,速度是60km/h,假如行驶过程中速度不变,汽车行驶路程用为23公里,聪明的你,能表示出汽车行驶的时间吗?
情境导入
如果汽车速度是vkm/h,路程是skm,汽车行驶的时间是多少?
出发时,我发现我的油箱里有8L油,根据以往的经验,发现每行驶100km耗油aL,那么汽车每千米耗油多少升?汽车剩余的油量还能行驶多少路程?
情境导入
我准备用a元钱去加油,发现92号汽油每升b元,加油站搞促销,每升降价1元,那么现在可以加油多少升?
到学校的途中,我打开了收音机,广播里面正在播放今早的相关新闻,我估算了一下主持人的语速达到每分钟180字,我听了t分钟,主持人在这个过程中大概播报了x个新闻事件,每个新闻事件播报的时间差不多,请问平均一个新闻事件大概播报多少字?
情境导入
回顾前面所列举的实例,观察下列数学式子:
讨论下面的问题:
⑴这些数学式子中哪些是整式?
⑵其余的式子为什么不是整式?它们具有哪些共同特征?
⑶你能给不是整式的式子命名吗?你是怎么想到的?
合作探究
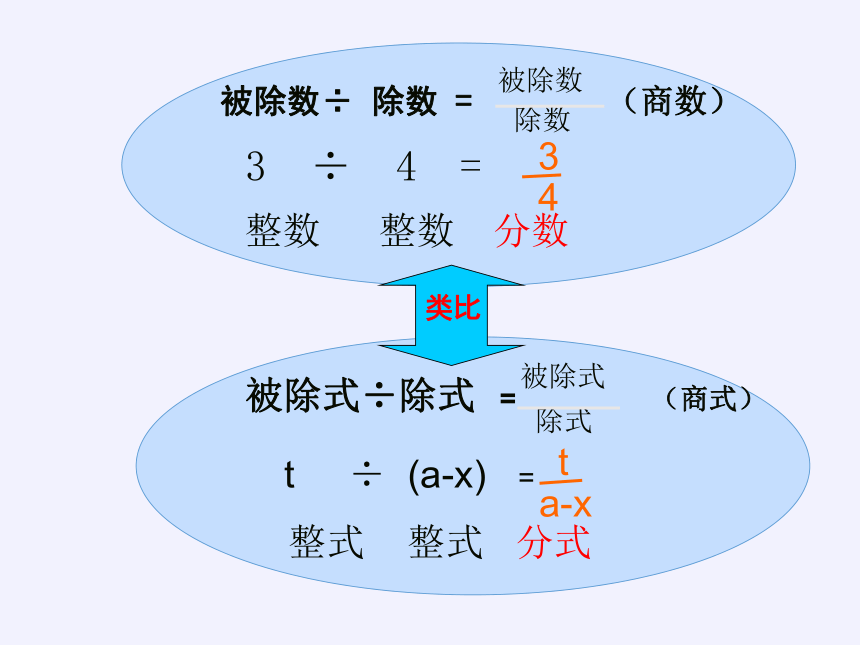
被除数
除数
3
4
被除数÷ 除数 = (商数)
整数 整数 分数
3 ÷ 4 =
被除式
除式
t
a-x
被除式÷除式 = (商式)
整式 整式 分式
t ÷ (a-x) =
类比
形成概念
一般地,如果A、B表示两个整式,并且B中含有字母,那么代数式 叫做分式。
其中A是分式的分子,B是分式的分母。
(2)
(3)
2a+b,
(4)
(5)
例1.请判断下列各式是否为分式?若不是,请说明理由。
(1)
(6)
√
×
×
×
√
√
典型例题
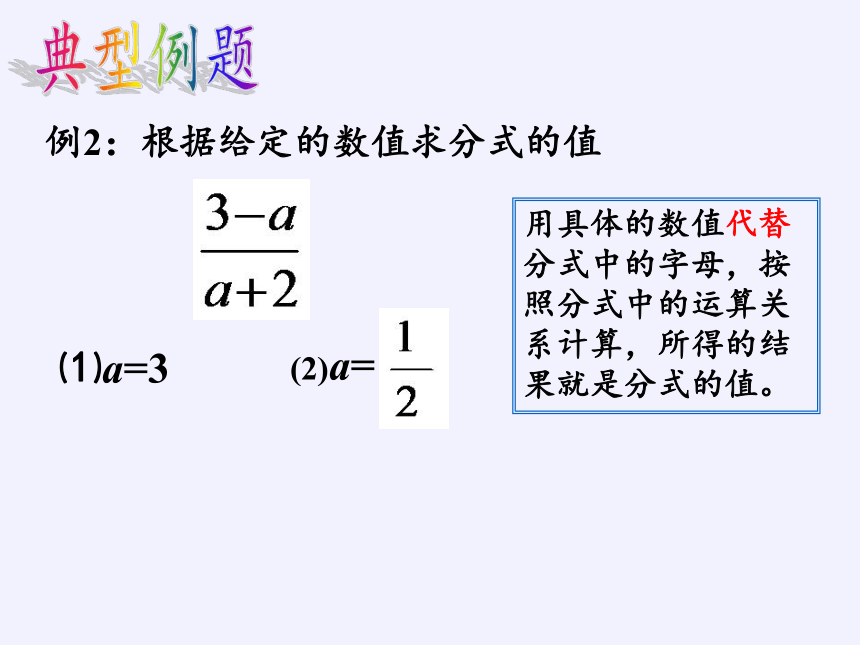
例2:根据给定的数值求分式的值
⑴a=3
(2)a=
用具体的数值代替分式中的字母,按照分式中的运算关系计算,所得的结果就是分式的值。
典型例题
典型例题
例3:对于分式
⑴当x取什么值时,分式有意义?
⑵当x取什么值时,分式无意义?
解:由分母x-2≠0,得x≠2
∴ 当x≠2时,分式有意义。
解:由分母x-2=0,得x=2
∴ 当x=2时,分式无意义。
分母为0,则分式无意义
分母不为0,则分式有意义
例4:对于分式
当x取何值时,值为0?
在分式中,当分子为零且分母不为零时,分式的值为零。
典型例题
1、当x取什么值时,分式
(1)无意义 (2)有意义?
2、当x取什么值时,分式 的值为0
练一练
我准备用a元钱去加油,发现92号汽油每升b
元,加油站搞促销,每升降价1元,那么现在
可以加油 升。
分式 还可以表示什么?
你说
我说
大家说
又如:如果a表示长方形的面积,b表示长方形的宽,
那么 表示宽减少1个单位长度后,面积仍为a的长方形的长。
例如:如果a(元)表示购买笔记本的钱数,b(元)表示每本笔记本的售价,那么 表示每本笔记降价1元后,用a元可购得笔记本的本数;
1
-
b
a
练习:1.当x取什么值时,下列分式的值为零。
⑴
⑵
牛刀小试
x -3 -2 -1 0 1 2 3
2.填表:
无意义
3.一个分子为x-5的分式,且知它在x≠1时有意义。你能写出一个符合上面条件的分式吗?试试看。
游戏
1
将其中2张卡片分别放在分子、分母上,
它们组成的式子是分式吗?如果是分式,它
什么时候有意义?
x
1-x
-3
我有话要说
通过本节课的学习,你有哪些收获?你还有哪些困惑?
课后作业
1.课本P100习题10.1第1-3题
2.设计一个分式,请同桌举例说明它的实际意义。
3.尽可能多地找出你所学过的与分式有关的知识内(如:已知三角形的面积为S,底边长为a,那么底边上的高线长h为 ),
a
s
2
于是,我选择了附近的加油站给汽车加油,假设到达加油站时,油箱里的油还有5升,加油站的服务人员热情接待了我,并说出如果加油总额超过200元可以打95折,我看了一下现在的油费是5.54元/升,油箱总容量为y 升(y>50), 如果我加满油,需要付费多少元?(列出式子即可)如果加油时间为t分钟,请问加油枪的流速是每分钟多少升?
情境导入
a … -2 -1 0 1 2 …
… …
… …
填表:
学以致用
3.当a的值分别为0.01、0.1、1、10、100时,
求分式 的值。随a的值变化, 的值
是如何变化的?
2.对于分式:
(1)如果x=1,那么y取何值时,分式无意义?
(2)使分式无意义的x、y有多少对?它们有什么关系?
(3)当x、y满足什么关系时,分式的值为0?
学以致用
谢 谢
10.1 分式
早晨,我开车前往学校的途中,速度是60km/h,假如行驶过程中速度不变,汽车行驶路程用为23公里,聪明的你,能表示出汽车行驶的时间吗?
情境导入
如果汽车速度是vkm/h,路程是skm,汽车行驶的时间是多少?
出发时,我发现我的油箱里有8L油,根据以往的经验,发现每行驶100km耗油aL,那么汽车每千米耗油多少升?汽车剩余的油量还能行驶多少路程?
情境导入
我准备用a元钱去加油,发现92号汽油每升b元,加油站搞促销,每升降价1元,那么现在可以加油多少升?
到学校的途中,我打开了收音机,广播里面正在播放今早的相关新闻,我估算了一下主持人的语速达到每分钟180字,我听了t分钟,主持人在这个过程中大概播报了x个新闻事件,每个新闻事件播报的时间差不多,请问平均一个新闻事件大概播报多少字?
情境导入
回顾前面所列举的实例,观察下列数学式子:
讨论下面的问题:
⑴这些数学式子中哪些是整式?
⑵其余的式子为什么不是整式?它们具有哪些共同特征?
⑶你能给不是整式的式子命名吗?你是怎么想到的?
合作探究
被除数
除数
3
4
被除数÷ 除数 = (商数)
整数 整数 分数
3 ÷ 4 =
被除式
除式
t
a-x
被除式÷除式 = (商式)
整式 整式 分式
t ÷ (a-x) =
类比
形成概念
一般地,如果A、B表示两个整式,并且B中含有字母,那么代数式 叫做分式。
其中A是分式的分子,B是分式的分母。
(2)
(3)
2a+b,
(4)
(5)
例1.请判断下列各式是否为分式?若不是,请说明理由。
(1)
(6)
√
×
×
×
√
√
典型例题
例2:根据给定的数值求分式的值
⑴a=3
(2)a=
用具体的数值代替分式中的字母,按照分式中的运算关系计算,所得的结果就是分式的值。
典型例题
典型例题
例3:对于分式
⑴当x取什么值时,分式有意义?
⑵当x取什么值时,分式无意义?
解:由分母x-2≠0,得x≠2
∴ 当x≠2时,分式有意义。
解:由分母x-2=0,得x=2
∴ 当x=2时,分式无意义。
分母为0,则分式无意义
分母不为0,则分式有意义
例4:对于分式
当x取何值时,值为0?
在分式中,当分子为零且分母不为零时,分式的值为零。
典型例题
1、当x取什么值时,分式
(1)无意义 (2)有意义?
2、当x取什么值时,分式 的值为0
练一练
我准备用a元钱去加油,发现92号汽油每升b
元,加油站搞促销,每升降价1元,那么现在
可以加油 升。
分式 还可以表示什么?
你说
我说
大家说
又如:如果a表示长方形的面积,b表示长方形的宽,
那么 表示宽减少1个单位长度后,面积仍为a的长方形的长。
例如:如果a(元)表示购买笔记本的钱数,b(元)表示每本笔记本的售价,那么 表示每本笔记降价1元后,用a元可购得笔记本的本数;
1
-
b
a
练习:1.当x取什么值时,下列分式的值为零。
⑴
⑵
牛刀小试
x -3 -2 -1 0 1 2 3
2.填表:
无意义
3.一个分子为x-5的分式,且知它在x≠1时有意义。你能写出一个符合上面条件的分式吗?试试看。
游戏
1
将其中2张卡片分别放在分子、分母上,
它们组成的式子是分式吗?如果是分式,它
什么时候有意义?
x
1-x
-3
我有话要说
通过本节课的学习,你有哪些收获?你还有哪些困惑?
课后作业
1.课本P100习题10.1第1-3题
2.设计一个分式,请同桌举例说明它的实际意义。
3.尽可能多地找出你所学过的与分式有关的知识内(如:已知三角形的面积为S,底边长为a,那么底边上的高线长h为 ),
a
s
2
于是,我选择了附近的加油站给汽车加油,假设到达加油站时,油箱里的油还有5升,加油站的服务人员热情接待了我,并说出如果加油总额超过200元可以打95折,我看了一下现在的油费是5.54元/升,油箱总容量为y 升(y>50), 如果我加满油,需要付费多少元?(列出式子即可)如果加油时间为t分钟,请问加油枪的流速是每分钟多少升?
情境导入
a … -2 -1 0 1 2 …
… …
… …
填表:
学以致用
3.当a的值分别为0.01、0.1、1、10、100时,
求分式 的值。随a的值变化, 的值
是如何变化的?
2.对于分式:
(1)如果x=1,那么y取何值时,分式无意义?
(2)使分式无意义的x、y有多少对?它们有什么关系?
(3)当x、y满足什么关系时,分式的值为0?
学以致用
谢 谢
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
