12.1 平面上点的坐标(1)
图片预览

文档简介
12.1 平面上点的坐标(1)
学习目标:
1.通过实际问题抽象出平面直角坐标系及其相关概念,认识平面直角坐标系原点、横轴和纵轴等.体会平面上的点与有序实数对之间的对应关系.
2.认识并能画出平面直角坐标系.
3.能够在给定的直角坐标系中,会由坐标描点,由点写出坐标;
学习重点:
正确认识平面直角坐标系,能由点写出坐标,由坐标描点.
学习难点:
各象限内坐标的符号及各坐标轴上点坐标的特点,平面上的点与有序实数对之间的对应关系.
一、学前准备
1.数轴:规定了______、_______、__________的_____叫做数轴
数轴上的点与______是一一对应.
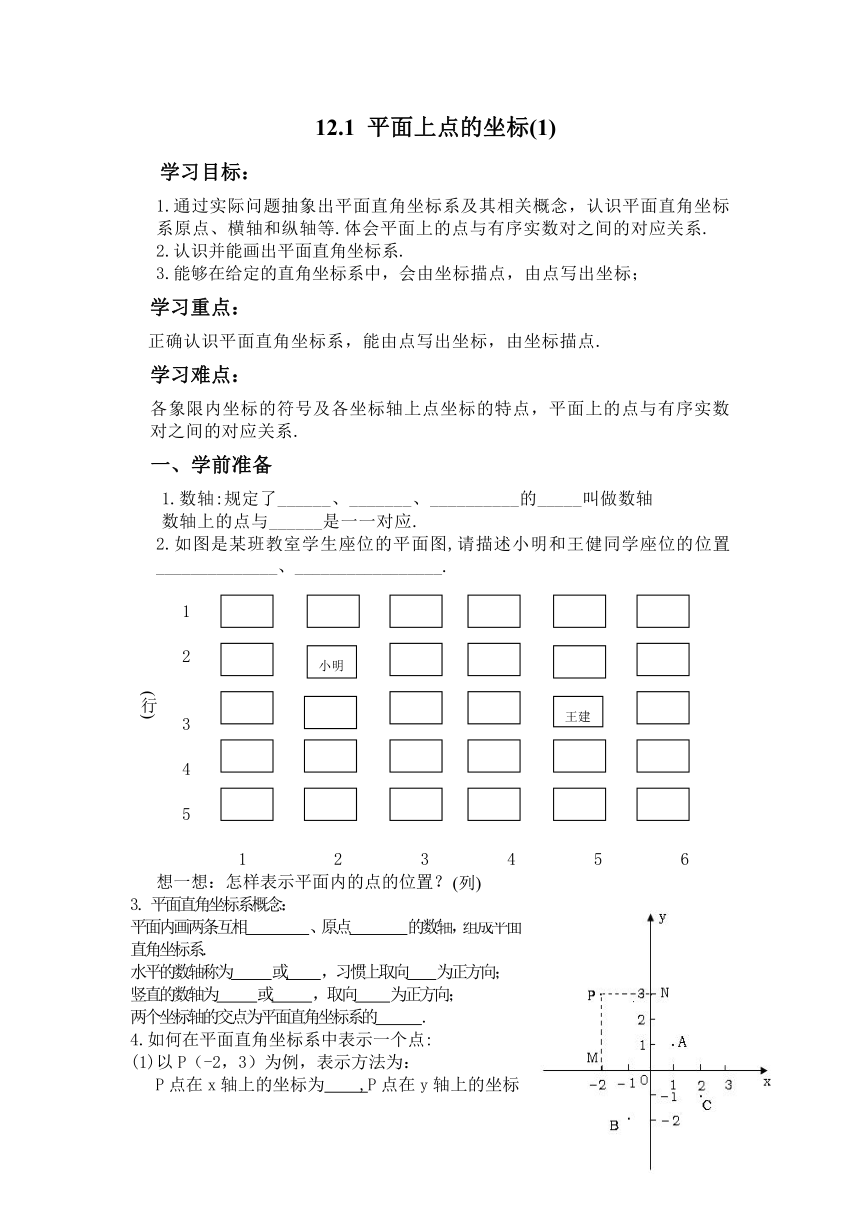
2.如图是某班教室学生座位的平面图,请描述小明和王健同学座位的位置______________、_________________.
1
2
3
4
5
1 2 3 4 5 6
想一想:怎样表示平面内的点的位置?
3. 平面直角坐标系概念:
平面内画两条互相 、原点 的数轴,组成平面直角坐标系.
水平的数轴称为 或 ,习惯上取向 为正方向;
竖直的数轴为 或 ,取向 为正方向;
两个坐标轴的交点为平面直角坐标系的 .
4.如何在平面直角坐标系中表示一个点:
(1)以P(-2,3)为例,表示方法为:
P点在x轴上的坐标为 ,P点在y轴上的坐标为 ,
P点在平面直角坐标系中的坐标为(-2,3),记作P(-2,3)
强调:X轴上的坐标写在前面。
(2)写出点A、B、C的坐标.______________________
(3)描点:G(0,1),H(1,0)(注意区别)
思考归纳:原点O的坐标是(___,____), 第二象限 第一象限
横轴上的点坐标为(___,___) , (___,____) (___,___)
纵轴上的点坐标为(__,___)
注意:平面上的点与有序实数对是一一对应的.
5.象限:(1) 建立平面直角坐标系后,
坐标平面被坐标轴分成四部分, 第三象限 第四象限
分别叫_________,__________, (___,___) (___,___)
__________和____________。
(2)注意:坐标轴上的点不属于任何一个象限
练一练:
1.点A(-3,2)在第_______象限,点D(-3,-2)在第_______象限,点C( 3, 2) 在第______象限,点D(-3,-2)在第_______象限,点E(0,2)在______轴上, 点F( 2, 0) 在______轴上.
2.若点M的坐标是(a,b),且a>0,b<0,则点M在( )
A.第一象限; B.第二象限; C.第三象限; D.第四象限
预习疑难摘要________________________________________________________
____________________________________________________________________
二、探究活动
(一)师生探究·解决问题
例1:把图中A、B、C、D、E、F各点对应的坐标填入下表:
点
横坐标
纵坐标
坐 标
A
4
2
(4,2)
B
C
D
E
F
例2:在平面直角坐标系中描出出下列各点:
A(3,4), B(3,-2),
C(-1,-4), D(-2,2),
E(2,0), F(0,-3)
(二)独立思考·巩固升华
填空:
坐标
点的位置
横 坐 标
纵 坐 标
第一象限
+
+
第二象限
第三象限
第四象限
X轴上 正半轴
负半轴
正半轴
Y轴上 负半轴
原 点
三、自我测试
1.如图1所示,点A的坐标是 ( )
A.(3,2); B.(3,3); C.(3,-3) ; D.(-3,-3)
2.如图1所示,横坐标和纵坐标都是负数的点是 ( )
A.A点 B.B点 C.C点 D.D点
3.如图1所示,坐标是(-2,2)的点是 ( )
A.点A B.点B C.点C D.点D
4.已知点M(a,b),当a>0,b>0时,M在第_____象限;当a____,b_____时,M 在第二象限;当a_____,b______时,M在第四象限;当a<0,b<0时,M在第_____象限.
四、应用与拓展
1.如果│3x-13y+16│+│x+3y-2│=0,那么点P(x,y)在第几象限?点Q(x+1,y-1)在坐标平面内的什么位置?
五、反思与修正
学习目标:
1.通过实际问题抽象出平面直角坐标系及其相关概念,认识平面直角坐标系原点、横轴和纵轴等.体会平面上的点与有序实数对之间的对应关系.
2.认识并能画出平面直角坐标系.
3.能够在给定的直角坐标系中,会由坐标描点,由点写出坐标;
学习重点:
正确认识平面直角坐标系,能由点写出坐标,由坐标描点.
学习难点:
各象限内坐标的符号及各坐标轴上点坐标的特点,平面上的点与有序实数对之间的对应关系.
一、学前准备
1.数轴:规定了______、_______、__________的_____叫做数轴
数轴上的点与______是一一对应.
2.如图是某班教室学生座位的平面图,请描述小明和王健同学座位的位置______________、_________________.
1
2
3
4
5
1 2 3 4 5 6
想一想:怎样表示平面内的点的位置?
3. 平面直角坐标系概念:
平面内画两条互相 、原点 的数轴,组成平面直角坐标系.
水平的数轴称为 或 ,习惯上取向 为正方向;
竖直的数轴为 或 ,取向 为正方向;
两个坐标轴的交点为平面直角坐标系的 .
4.如何在平面直角坐标系中表示一个点:
(1)以P(-2,3)为例,表示方法为:
P点在x轴上的坐标为 ,P点在y轴上的坐标为 ,
P点在平面直角坐标系中的坐标为(-2,3),记作P(-2,3)
强调:X轴上的坐标写在前面。
(2)写出点A、B、C的坐标.______________________
(3)描点:G(0,1),H(1,0)(注意区别)
思考归纳:原点O的坐标是(___,____), 第二象限 第一象限
横轴上的点坐标为(___,___) , (___,____) (___,___)
纵轴上的点坐标为(__,___)
注意:平面上的点与有序实数对是一一对应的.
5.象限:(1) 建立平面直角坐标系后,
坐标平面被坐标轴分成四部分, 第三象限 第四象限
分别叫_________,__________, (___,___) (___,___)
__________和____________。
(2)注意:坐标轴上的点不属于任何一个象限
练一练:
1.点A(-3,2)在第_______象限,点D(-3,-2)在第_______象限,点C( 3, 2) 在第______象限,点D(-3,-2)在第_______象限,点E(0,2)在______轴上, 点F( 2, 0) 在______轴上.
2.若点M的坐标是(a,b),且a>0,b<0,则点M在( )
A.第一象限; B.第二象限; C.第三象限; D.第四象限
预习疑难摘要________________________________________________________
____________________________________________________________________
二、探究活动
(一)师生探究·解决问题
例1:把图中A、B、C、D、E、F各点对应的坐标填入下表:
点
横坐标
纵坐标
坐 标
A
4
2
(4,2)
B
C
D
E
F
例2:在平面直角坐标系中描出出下列各点:
A(3,4), B(3,-2),
C(-1,-4), D(-2,2),
E(2,0), F(0,-3)
(二)独立思考·巩固升华
填空:
坐标
点的位置
横 坐 标
纵 坐 标
第一象限
+
+
第二象限
第三象限
第四象限
X轴上 正半轴
负半轴
正半轴
Y轴上 负半轴
原 点
三、自我测试
1.如图1所示,点A的坐标是 ( )
A.(3,2); B.(3,3); C.(3,-3) ; D.(-3,-3)
2.如图1所示,横坐标和纵坐标都是负数的点是 ( )
A.A点 B.B点 C.C点 D.D点
3.如图1所示,坐标是(-2,2)的点是 ( )
A.点A B.点B C.点C D.点D
4.已知点M(a,b),当a>0,b>0时,M在第_____象限;当a____,b_____时,M 在第二象限;当a_____,b______时,M在第四象限;当a<0,b<0时,M在第_____象限.
四、应用与拓展
1.如果│3x-13y+16│+│x+3y-2│=0,那么点P(x,y)在第几象限?点Q(x+1,y-1)在坐标平面内的什么位置?
五、反思与修正
