12.1 平面上点的坐标(2)
图片预览
文档简介
12.1 平面上点的坐标(2)
学习目标:
1、通过找点、连线、观察,确定图形的大致形状并能计算图形的面积.
2、会根据实际情况建立适当的坐标系.
3、通过点的位置关系探索坐标之间的关系以及根据坐标之间的关系探索点的位置关系,体会平面直角坐标系在实际中的应用.
学习重点::
会根据实际情况建立适当的坐标系,用平面直角坐标系表示具体的地理位置.
学习难点:
通过点的位置关系探索坐标之间的关系以及根据坐标之间的关系探索点的位置关系
一、学前准备
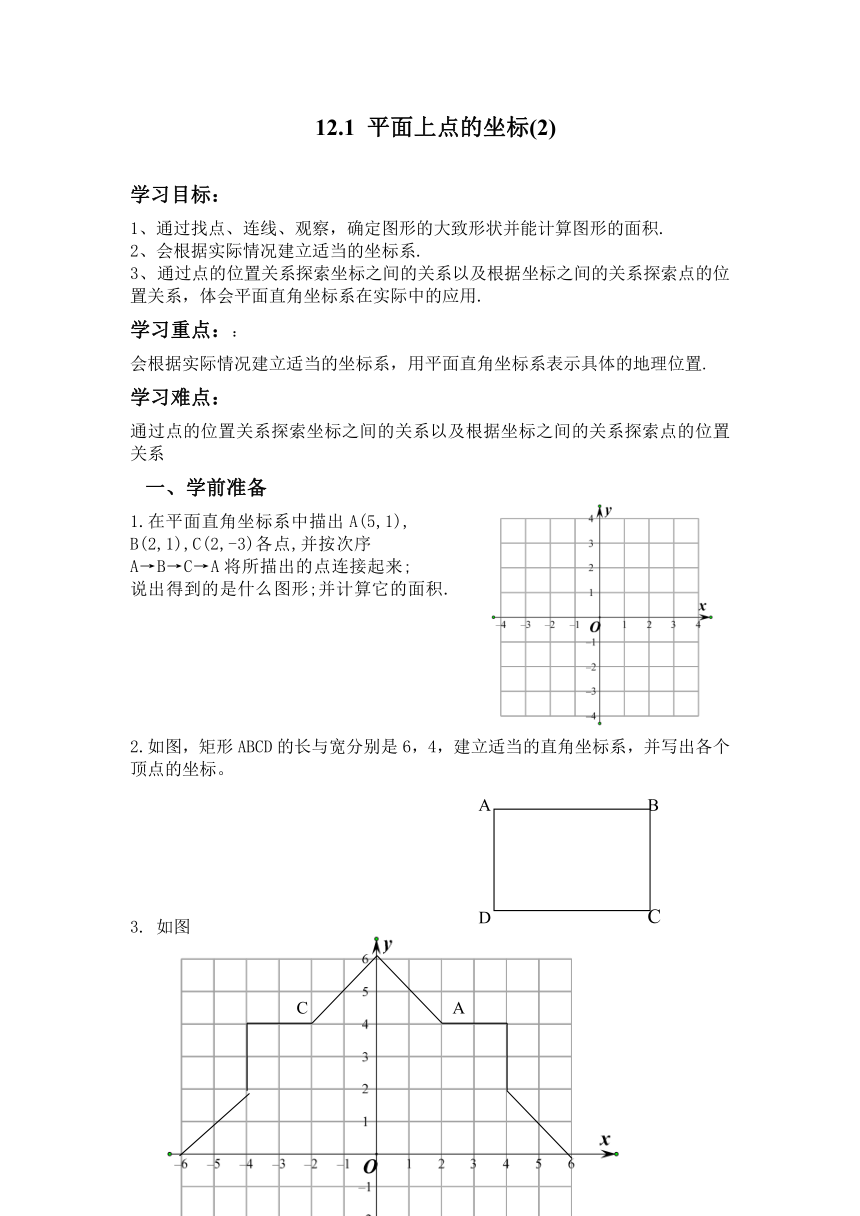
1.在平面直角坐标系中描出A(5,1),
B(2,1),C(2,-3)各点,并按次序
A→B→C→A将所描出的点连接起来;
说出得到的是什么图形;并计算它的面积.
2.如图,矩形ABCD的长与宽分别是6,4,建立适当的直角坐标系,并写出各个顶点的坐标。
3. 如图
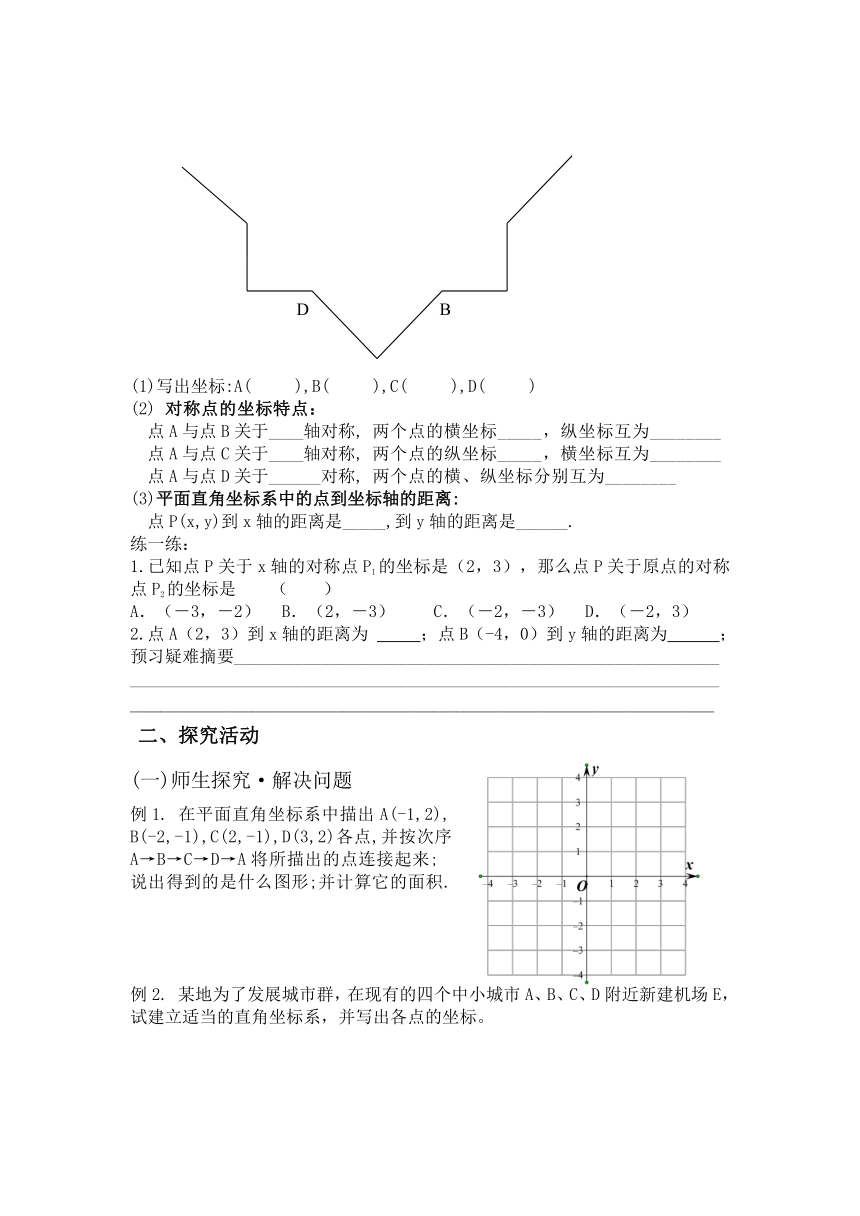
(1)写出坐标:A( ),B( ),C( ),D( )
(2) 对称点的坐标特点:
点A与点B关于____轴对称, 两个点的横坐标_____,纵坐标互为________
点A与点C关于____轴对称, 两个点的纵坐标_____,横坐标互为________
点A与点D关于______对称, 两个点的横、纵坐标分别互为________
(3)平面直角坐标系中的点到坐标轴的距离:
点P(x,y)到x轴的距离是_____,到y轴的距离是______.
练一练:
1.已知点P关于x轴的对称点P1的坐标是(2,3),那么点P关于原点的对称点P2的坐标是 ( ) A.(-3,-2) B.(2,-3) C.(-2,-3) D.(-2,3)
2.点A(2,3)到x轴的距离为 ;点B(-4,0)到y轴的距离为 ;
预习疑难摘要________________________________________________________
____________________________________________________________________
_____________________________________________________________________________
二、探究活动
(一)师生探究·解决问题
例1. 在平面直角坐标系中描出A(-1,2),
B(-2,-1),C(2,-1),D(3,2)各点,并按次序
A→B→C→D→A将所描出的点连接起来;
说出得到的是什么图形;并计算它的面积.
例2. 某地为了发展城市群,在现有的四个中小城市A、B、C、D附近新建机场E,试建立适当的直角坐标系,并写出各点的坐标。
(二)独立思考·巩固升华
1.矩形ABCD中,三点的坐标分别是(0,0);(5,0);(5,3).则第四点的坐标是( )
A.(0,3) B.(3,0) C.(0,5) D.(5,0)
2.点C到x轴的距离为1,到y轴的距离为3,且在第三象限,则C点坐标是 __
三、自我测试
1. (1)假如你想让你的同学在看不到图形的情况下,准确地
画出如图所示小船图案,你怎样来描述
(2)计算图中小船图案面积
2. 建立一个平面直角坐标系,.
用坐标表示图中各点的位置
四、应用与拓展
1.已知点A(-4,2),点B(3,2),那么A、B的直线与坐标轴有的位置关系是
______________________________________________________.
2. 已知点C(2,-4),点D(2,3),那么C、D的直线与坐标轴有的位置关系是
_______________________________________________________.
五、反思与修正
学习目标:
1、通过找点、连线、观察,确定图形的大致形状并能计算图形的面积.
2、会根据实际情况建立适当的坐标系.
3、通过点的位置关系探索坐标之间的关系以及根据坐标之间的关系探索点的位置关系,体会平面直角坐标系在实际中的应用.
学习重点::
会根据实际情况建立适当的坐标系,用平面直角坐标系表示具体的地理位置.
学习难点:
通过点的位置关系探索坐标之间的关系以及根据坐标之间的关系探索点的位置关系
一、学前准备
1.在平面直角坐标系中描出A(5,1),
B(2,1),C(2,-3)各点,并按次序
A→B→C→A将所描出的点连接起来;
说出得到的是什么图形;并计算它的面积.
2.如图,矩形ABCD的长与宽分别是6,4,建立适当的直角坐标系,并写出各个顶点的坐标。
3. 如图
(1)写出坐标:A( ),B( ),C( ),D( )
(2) 对称点的坐标特点:
点A与点B关于____轴对称, 两个点的横坐标_____,纵坐标互为________
点A与点C关于____轴对称, 两个点的纵坐标_____,横坐标互为________
点A与点D关于______对称, 两个点的横、纵坐标分别互为________
(3)平面直角坐标系中的点到坐标轴的距离:
点P(x,y)到x轴的距离是_____,到y轴的距离是______.
练一练:
1.已知点P关于x轴的对称点P1的坐标是(2,3),那么点P关于原点的对称点P2的坐标是 ( ) A.(-3,-2) B.(2,-3) C.(-2,-3) D.(-2,3)
2.点A(2,3)到x轴的距离为 ;点B(-4,0)到y轴的距离为 ;
预习疑难摘要________________________________________________________
____________________________________________________________________
_____________________________________________________________________________
二、探究活动
(一)师生探究·解决问题
例1. 在平面直角坐标系中描出A(-1,2),
B(-2,-1),C(2,-1),D(3,2)各点,并按次序
A→B→C→D→A将所描出的点连接起来;
说出得到的是什么图形;并计算它的面积.
例2. 某地为了发展城市群,在现有的四个中小城市A、B、C、D附近新建机场E,试建立适当的直角坐标系,并写出各点的坐标。
(二)独立思考·巩固升华
1.矩形ABCD中,三点的坐标分别是(0,0);(5,0);(5,3).则第四点的坐标是( )
A.(0,3) B.(3,0) C.(0,5) D.(5,0)
2.点C到x轴的距离为1,到y轴的距离为3,且在第三象限,则C点坐标是 __
三、自我测试
1. (1)假如你想让你的同学在看不到图形的情况下,准确地
画出如图所示小船图案,你怎样来描述
(2)计算图中小船图案面积
2. 建立一个平面直角坐标系,.
用坐标表示图中各点的位置
四、应用与拓展
1.已知点A(-4,2),点B(3,2),那么A、B的直线与坐标轴有的位置关系是
______________________________________________________.
2. 已知点C(2,-4),点D(2,3),那么C、D的直线与坐标轴有的位置关系是
_______________________________________________________.
五、反思与修正
