12.2 图形在坐标系中的平移
图片预览
文档简介
12.2 图形在坐标系中的平移
学习目标:
1、能在直角坐标系中用坐标的方法研究图形的变换,掌握图形在平移过程中各点坐标的变化规律,理解图形在平面坐标系上的平移实质上就是点坐标的对应变换;
2、运用图形在直角坐标系中平移的点坐标的变化规律进行简单的平移作图;
3、经历观察、分析、抽象、归纳等过程,经历与他人合作交流的过程进一步发展数形结合的思想与空间观念。
学习重点::
掌握用坐标系的变化规律来描述平移的过程.
学习难点:
根据图形的平移过程,探索、归纳出坐标的变化规律
一、学前准备
1. 点的坐标变化与平移间的关系
(1)实验探索
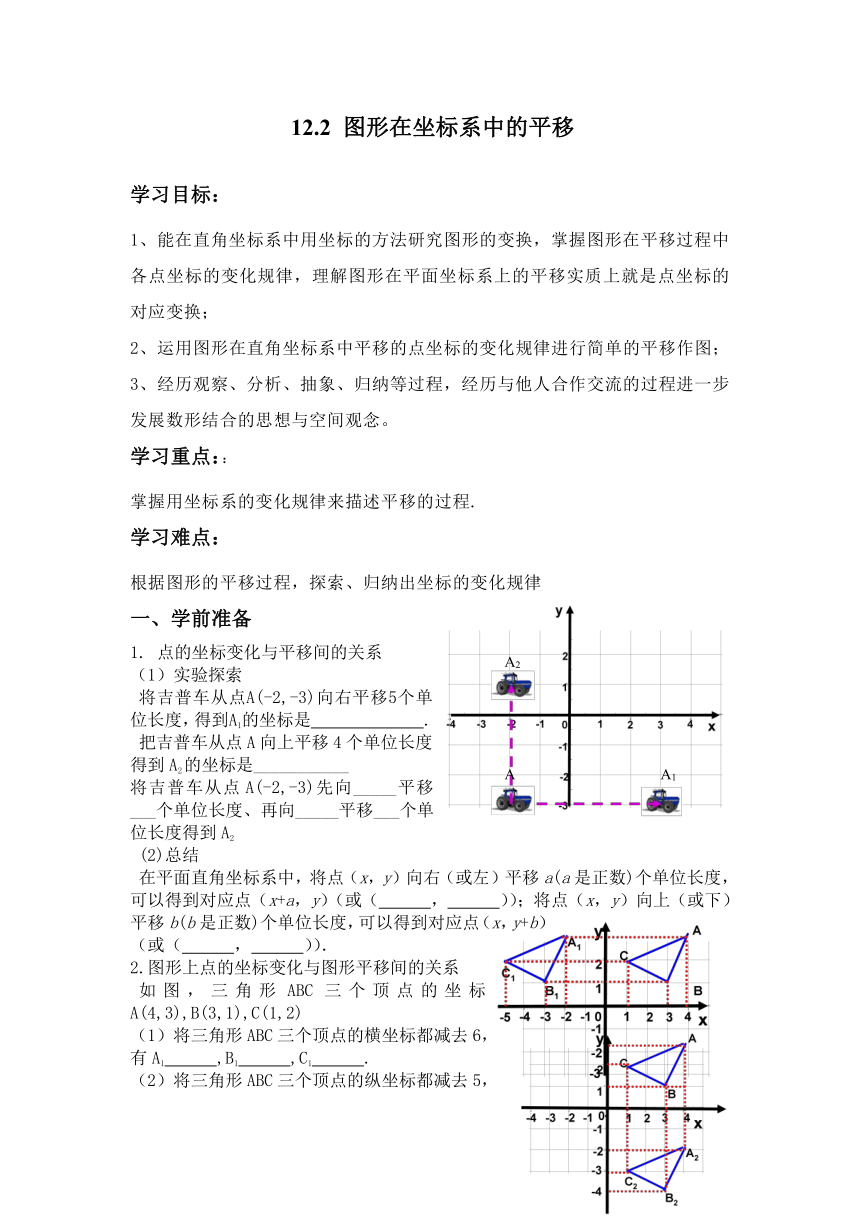
将吉普车从点A(-2,-3)向右平移5个单位长度,得到A1的坐标是 .
把吉普车从点A向上平移4个单位长度得到A2的坐标是___________
将吉普车从点A(-2,-3)先向_____平移___个单位长度、再向_____平移___个单位长度得到A2
(2)总结
在平面直角坐标系中,将点(x,y)向右(或左)平移a(a是正数)个单位长度,可以得到对应点(x+a,y)(或( , ));将点(x,y)向上(或下)平移b(b是正数)个单位长度,可以得到对应点(x,y+b)(或( , )).
2.图形上点的坐标变化与图形平移间的关系
如图,三角形ABC三个顶点的坐标A(4,3),B(3,1),C(1,2)
(1)将三角形ABC三个顶点的横坐标都减去6,有A1 ,B1 ,C1 .
(2)将三角形ABC三个顶点的纵坐标都减去5,
有A2 ,B2 ,C2 .
(3)将三角形ABC三个顶点的横坐标都
减 6,纵坐标减5,有A2 ,B2 ,C2 .
(4)归纳:在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向__ _(或向_ ___)平移_ __个单位长度;如果把它各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向__ _(或向 _ _) 平移__ _个单位长度.即“上加下减,左减右加”
练一练:
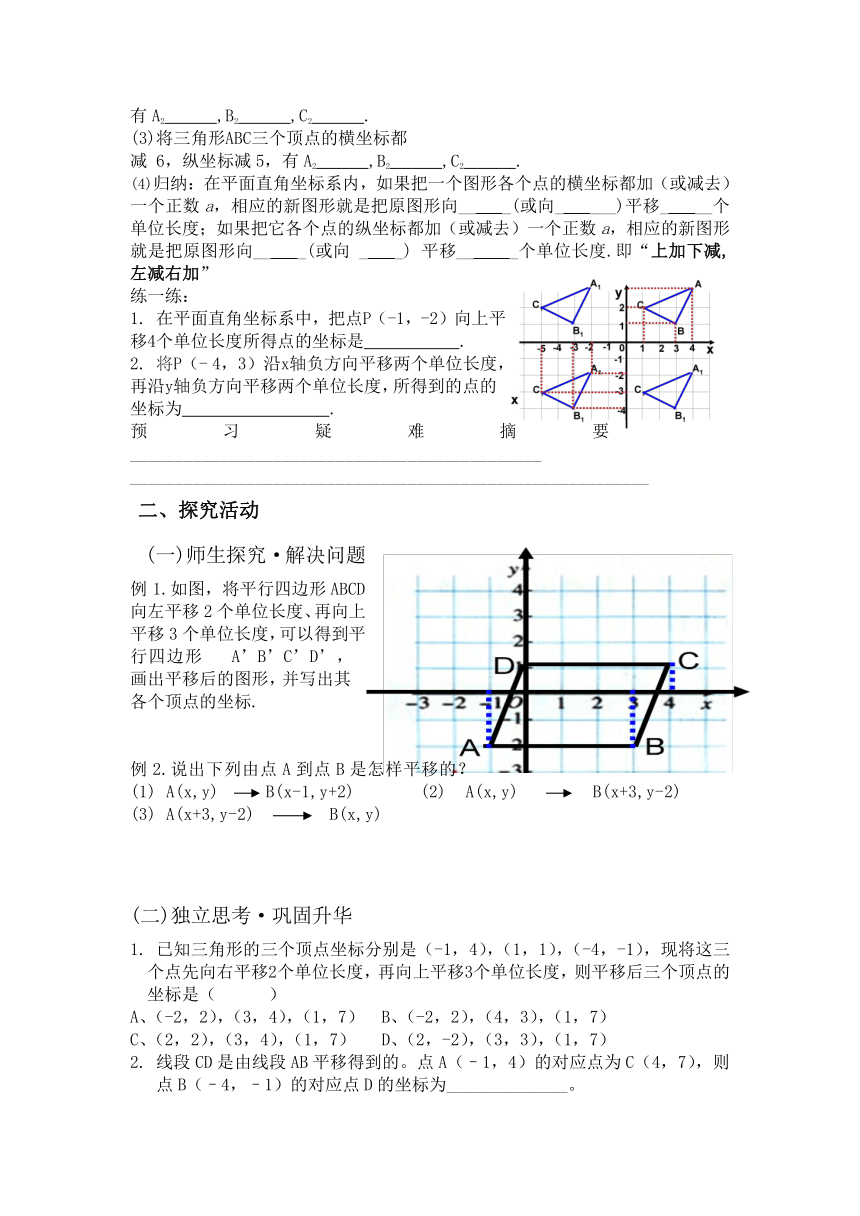
1. 在平面直角坐标系中,把点P(-1,-2)向上平移4个单位长度所得点的坐标是 .
2. 将P(- 4,3)沿x轴负方向平移两个单位长度,再沿y轴负方向平移两个单位长度,所得到的点的坐标为 .
预习疑难摘要______________________________________________
__________________________________________________________
二、探究活动
(一)师生探究·解决问题
例1.如图,将平行四边形ABCD向左平移2个单位长度、再向上平移3个单位长度,可以得到平行四边形 A’B’C’D’,画出平移后的图形,并写出其各个顶点的坐标.
例2.说出下列由点A到点B是怎样平移的?
(1) A(x,y) B(x-1,y+2) (2) A(x,y) B(x+3,y-2)
(3) A(x+3,y-2) B(x,y)
(二)独立思考·巩固升华
1. 已知三角形的三个顶点坐标分别是(-1,4),(1,1),(-4,-1),现将这三个点先向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标是( )
A、(-2,2),(3,4),(1,7) B、(-2,2),(4,3),(1,7)
C、(2,2),(3,4),(1,7) D、(2,-2),(3,3),(1,7)
2. 线段CD是由线段AB平移得到的。点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为______________。
三、自我测试
1. 将点P(-3,y)向下平移3个单位,向左平移2个单位后得到点Q(x,-1),则xy=_______ .
2. 三角形DEF是由三角形ABC平移得到的,点A(-1,-4)的对应点为D(1,-1),则点B(1,1)的对应点E、点C(-1,4)的对应点F的坐标分别为 ( )
A、(2,2),(3,4) B、(3,4),(1,7)
C、(-2,2),(1,7) D、(3,4),(2,-2)
3.如图,三角形ABC中任意一点经平移后对应点为,将三角形ABC作同样的平移得到三角形.画出三角形,并写出三个顶点的坐标.
四、应用与拓展
1.如图所示的鱼是将坐标为(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)作如下变化:
①纵坐标保持不变,横坐标分别变成原来的2倍;
②横坐标保持不变,纵坐标分别变成原来的2倍;
③纵坐标、横坐标分别变成原来的2倍;
再将所得的点用线段依次连接起来,所得图案与
原来图案相比有什么变化?
五、反思与修正
学习目标:
1、能在直角坐标系中用坐标的方法研究图形的变换,掌握图形在平移过程中各点坐标的变化规律,理解图形在平面坐标系上的平移实质上就是点坐标的对应变换;
2、运用图形在直角坐标系中平移的点坐标的变化规律进行简单的平移作图;
3、经历观察、分析、抽象、归纳等过程,经历与他人合作交流的过程进一步发展数形结合的思想与空间观念。
学习重点::
掌握用坐标系的变化规律来描述平移的过程.
学习难点:
根据图形的平移过程,探索、归纳出坐标的变化规律
一、学前准备
1. 点的坐标变化与平移间的关系
(1)实验探索
将吉普车从点A(-2,-3)向右平移5个单位长度,得到A1的坐标是 .
把吉普车从点A向上平移4个单位长度得到A2的坐标是___________
将吉普车从点A(-2,-3)先向_____平移___个单位长度、再向_____平移___个单位长度得到A2
(2)总结
在平面直角坐标系中,将点(x,y)向右(或左)平移a(a是正数)个单位长度,可以得到对应点(x+a,y)(或( , ));将点(x,y)向上(或下)平移b(b是正数)个单位长度,可以得到对应点(x,y+b)(或( , )).
2.图形上点的坐标变化与图形平移间的关系
如图,三角形ABC三个顶点的坐标A(4,3),B(3,1),C(1,2)
(1)将三角形ABC三个顶点的横坐标都减去6,有A1 ,B1 ,C1 .
(2)将三角形ABC三个顶点的纵坐标都减去5,
有A2 ,B2 ,C2 .
(3)将三角形ABC三个顶点的横坐标都
减 6,纵坐标减5,有A2 ,B2 ,C2 .
(4)归纳:在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向__ _(或向_ ___)平移_ __个单位长度;如果把它各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向__ _(或向 _ _) 平移__ _个单位长度.即“上加下减,左减右加”
练一练:
1. 在平面直角坐标系中,把点P(-1,-2)向上平移4个单位长度所得点的坐标是 .
2. 将P(- 4,3)沿x轴负方向平移两个单位长度,再沿y轴负方向平移两个单位长度,所得到的点的坐标为 .
预习疑难摘要______________________________________________
__________________________________________________________
二、探究活动
(一)师生探究·解决问题
例1.如图,将平行四边形ABCD向左平移2个单位长度、再向上平移3个单位长度,可以得到平行四边形 A’B’C’D’,画出平移后的图形,并写出其各个顶点的坐标.
例2.说出下列由点A到点B是怎样平移的?
(1) A(x,y) B(x-1,y+2) (2) A(x,y) B(x+3,y-2)
(3) A(x+3,y-2) B(x,y)
(二)独立思考·巩固升华
1. 已知三角形的三个顶点坐标分别是(-1,4),(1,1),(-4,-1),现将这三个点先向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标是( )
A、(-2,2),(3,4),(1,7) B、(-2,2),(4,3),(1,7)
C、(2,2),(3,4),(1,7) D、(2,-2),(3,3),(1,7)
2. 线段CD是由线段AB平移得到的。点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为______________。
三、自我测试
1. 将点P(-3,y)向下平移3个单位,向左平移2个单位后得到点Q(x,-1),则xy=_______ .
2. 三角形DEF是由三角形ABC平移得到的,点A(-1,-4)的对应点为D(1,-1),则点B(1,1)的对应点E、点C(-1,4)的对应点F的坐标分别为 ( )
A、(2,2),(3,4) B、(3,4),(1,7)
C、(-2,2),(1,7) D、(3,4),(2,-2)
3.如图,三角形ABC中任意一点经平移后对应点为,将三角形ABC作同样的平移得到三角形.画出三角形,并写出三个顶点的坐标.
四、应用与拓展
1.如图所示的鱼是将坐标为(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)作如下变化:
①纵坐标保持不变,横坐标分别变成原来的2倍;
②横坐标保持不变,纵坐标分别变成原来的2倍;
③纵坐标、横坐标分别变成原来的2倍;
再将所得的点用线段依次连接起来,所得图案与
原来图案相比有什么变化?
五、反思与修正
