13.1函数(1)
图片预览

文档简介
13.1函数(1)
学习目标:
1.了解常量、变量的意义,能分清实例中出现的常量,变量与自变量和函数.
2.了解函数的意义,会举出函数的实例,并能写出简单的函数关系式;
学习重点::
在了解函数、常量、变量的基础上,能指出实例中的常量、变量,并能写出简单的函数关系式.
学习难点:
是对函数意义的正确理解.
一、学前准备
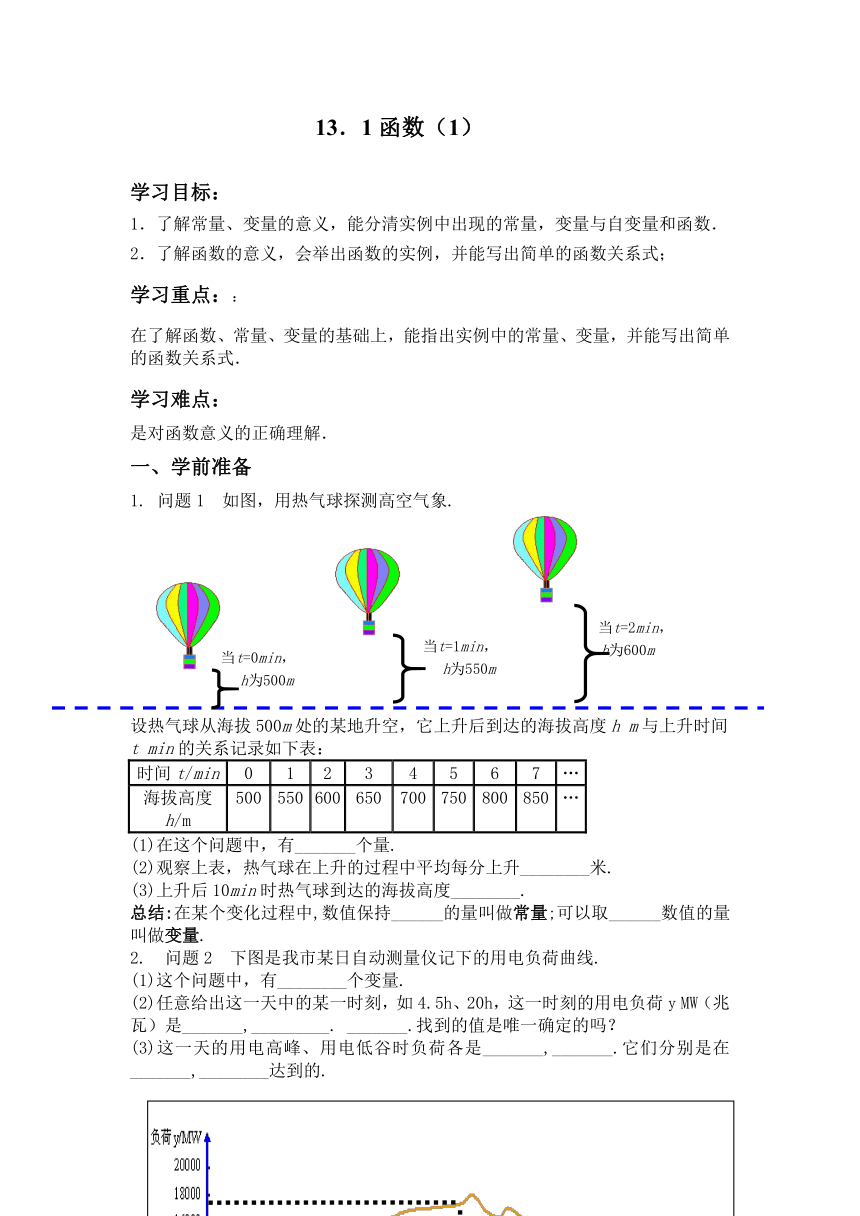
1. 问题1 如图,用热气球探测高空气象.
设热气球从海拔500m处的某地升空,它上升后到达的海拔高度h m与上升时间t min的关系记录如下表:
时间t/min
0
1
2
3
4
5
6
7
…
海拔高度h/m
500
550
600
650
700
750
800
850
…
(1)在这个问题中,有_______个量.
(2)观察上表,热气球在上升的过程中平均每分上升________米.
(3)上升后10min时热气球到达的海拔高度________.
总结:在某个变化过程中,数值保持______的量叫做常量;可以取______数值的量叫做变量.
2. 问题2 下图是我市某日自动测量仪记下的用电负荷曲线.
(1)这个问题中,有________个变量.
(2)任意给出这一天中的某一时刻,如4.5h、20h,这一时刻的用电负荷y MW(兆瓦)是_______,_________. _______.找到的值是唯一确定的吗?
(3)这一天的用电高峰、用电低谷时负荷各是_______,_______.它们分别是在_______,________达到的.
3. 问题3 汽车在行驶过程中,由于惯性的作用刹车后仍将滑行一段距离才能停住,刹车距离是分析事故原因的一个重要因素。
某型号的汽车在平整路面上的刹车距离sm与车速vkm/h之间有下列经验公式:
(1)上式中涉及哪几个量?_________________________________________.
(2)当刹车时车速v 分别是40、80、120km/h时,相应的滑行距离s分别是多少?___________,________________,_________________.
总结:在上面三个问题中,每个变化过程都只涉及两个变量,当给定其中一个变量(这个量叫_______)的值,相应地就确定了另一个变量(这个量叫______)的值.
函数:一般地,设在一个变化过程中有两个变量x与y,如果对于x在它允许取值范围内的_________,y都有_______的值与它对应,那么我们就说x是______,y是x的_______.
注意:(1)在一个变化过程中;(2)有两个变量(字母x与y只是代号);(3)对于x的每一个值,y都有唯一确定的值与其对应。
练一练:
1、在圆的周长公式C=2πR中,变量是 ,常量是 ,若用C来表示R,则表达式是 .
2、一辆汽车以60km/h的速度行驶,设行驶的路程为s(km),行驶的时间为t(h),则s与t的关系式为 ,自变量是 ,因变量是__________.
预习疑难摘要_____________________________________________________
_________________________________________________________________
二、探究活动
(一)师生探究·解决问题
例1:写出下列问题中变量间的关系式,并指出式中的常量与变量,自变量与因变量:购买单价是2.5元的圆珠笔,总金额y元与圆珠笔数n支的关系.
例2:如图,下列各曲线中哪些能够表示y是x的函数?为什么?
A B C D
(二)独立思考·巩固升华
1.指出下列关系式中的变量与常量:球的表面积S cm2与球的半径R cm的关系式是:S=4πR2.
2.下列与的关系式中,是的函数是( )
A. B. C. D.
三、自我测试
1、一幢商住楼底层为店面房,底层高为4米,底层以上每层高3米,则楼高h与层数n之间的函数关系式为 ,其中可以将 看成自变量, 是因变量,_______是______的函数.
2. 某电信公司手机费的收费标准如下表:
通话时间x(分)
0123………
费用y(元)
0.6
1.2
1.8
2.4
………
(1) 当使用该种收费方式的手机通话时间分别为1分30秒,2分10秒,3分,所需交的通话费分别是多少?
(2)给定一个x值,y都有唯一的值与它对应吗?y是x的函数吗?
四、应用与拓展
6、下列图形都是由若干个棋子围成的方形图案,图案的每条边(包括两个顶点)上都有n个棋子,每个图案的棋子总数为s,根据下图的规律用式子表示出s与n的关系______________,其中的变量是_______,常量是__________.
五、反思与修正
学习目标:
1.了解常量、变量的意义,能分清实例中出现的常量,变量与自变量和函数.
2.了解函数的意义,会举出函数的实例,并能写出简单的函数关系式;
学习重点::
在了解函数、常量、变量的基础上,能指出实例中的常量、变量,并能写出简单的函数关系式.
学习难点:
是对函数意义的正确理解.
一、学前准备
1. 问题1 如图,用热气球探测高空气象.
设热气球从海拔500m处的某地升空,它上升后到达的海拔高度h m与上升时间t min的关系记录如下表:
时间t/min
0
1
2
3
4
5
6
7
…
海拔高度h/m
500
550
600
650
700
750
800
850
…
(1)在这个问题中,有_______个量.
(2)观察上表,热气球在上升的过程中平均每分上升________米.
(3)上升后10min时热气球到达的海拔高度________.
总结:在某个变化过程中,数值保持______的量叫做常量;可以取______数值的量叫做变量.
2. 问题2 下图是我市某日自动测量仪记下的用电负荷曲线.
(1)这个问题中,有________个变量.
(2)任意给出这一天中的某一时刻,如4.5h、20h,这一时刻的用电负荷y MW(兆瓦)是_______,_________. _______.找到的值是唯一确定的吗?
(3)这一天的用电高峰、用电低谷时负荷各是_______,_______.它们分别是在_______,________达到的.
3. 问题3 汽车在行驶过程中,由于惯性的作用刹车后仍将滑行一段距离才能停住,刹车距离是分析事故原因的一个重要因素。
某型号的汽车在平整路面上的刹车距离sm与车速vkm/h之间有下列经验公式:
(1)上式中涉及哪几个量?_________________________________________.
(2)当刹车时车速v 分别是40、80、120km/h时,相应的滑行距离s分别是多少?___________,________________,_________________.
总结:在上面三个问题中,每个变化过程都只涉及两个变量,当给定其中一个变量(这个量叫_______)的值,相应地就确定了另一个变量(这个量叫______)的值.
函数:一般地,设在一个变化过程中有两个变量x与y,如果对于x在它允许取值范围内的_________,y都有_______的值与它对应,那么我们就说x是______,y是x的_______.
注意:(1)在一个变化过程中;(2)有两个变量(字母x与y只是代号);(3)对于x的每一个值,y都有唯一确定的值与其对应。
练一练:
1、在圆的周长公式C=2πR中,变量是 ,常量是 ,若用C来表示R,则表达式是 .
2、一辆汽车以60km/h的速度行驶,设行驶的路程为s(km),行驶的时间为t(h),则s与t的关系式为 ,自变量是 ,因变量是__________.
预习疑难摘要_____________________________________________________
_________________________________________________________________
二、探究活动
(一)师生探究·解决问题
例1:写出下列问题中变量间的关系式,并指出式中的常量与变量,自变量与因变量:购买单价是2.5元的圆珠笔,总金额y元与圆珠笔数n支的关系.
例2:如图,下列各曲线中哪些能够表示y是x的函数?为什么?
A B C D
(二)独立思考·巩固升华
1.指出下列关系式中的变量与常量:球的表面积S cm2与球的半径R cm的关系式是:S=4πR2.
2.下列与的关系式中,是的函数是( )
A. B. C. D.
三、自我测试
1、一幢商住楼底层为店面房,底层高为4米,底层以上每层高3米,则楼高h与层数n之间的函数关系式为 ,其中可以将 看成自变量, 是因变量,_______是______的函数.
2. 某电信公司手机费的收费标准如下表:
通话时间x(分)
0
费用y(元)
0.6
1.2
1.8
2.4
………
(1) 当使用该种收费方式的手机通话时间分别为1分30秒,2分10秒,3分,所需交的通话费分别是多少?
(2)给定一个x值,y都有唯一的值与它对应吗?y是x的函数吗?
四、应用与拓展
6、下列图形都是由若干个棋子围成的方形图案,图案的每条边(包括两个顶点)上都有n个棋子,每个图案的棋子总数为s,根据下图的规律用式子表示出s与n的关系______________,其中的变量是_______,常量是__________.
五、反思与修正
