西师大版六年级下学期数学2.1.4圆柱的体积课件(共19张PPT)
文档属性
| 名称 | 西师大版六年级下学期数学2.1.4圆柱的体积课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-03 08:34:34 | ||
图片预览





文档简介
(共19张PPT)
圆柱的体积练习课
情境导入
基础练习
课堂小结
课后作业
圆柱和圆锥
强化练习
2
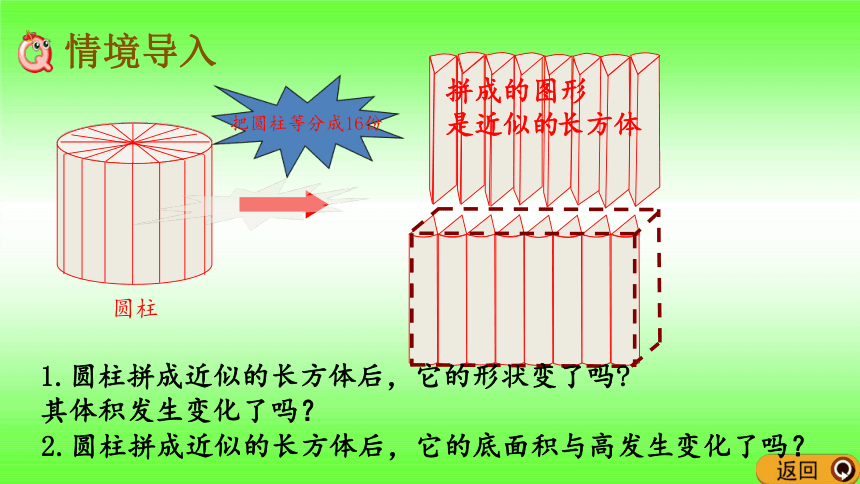
情境导入
长方体
圆柱
拼成的图形是近似的
把圆柱等分成16份
1.圆柱拼成近似的长方体后,它的形状变了吗
其体积发生变化了吗?
2.圆柱拼成近似的长方体后,它的底面积与高发生变化了吗?
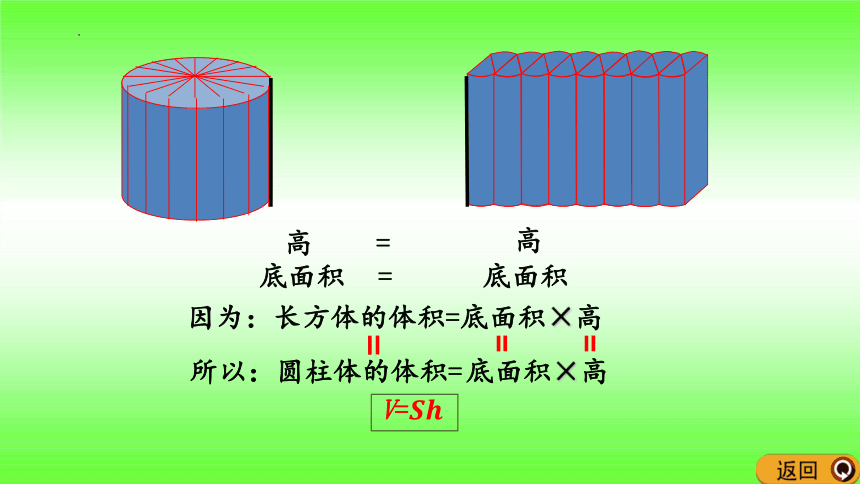
高
底面积
高
=
底面积
=
因为:长方体的体积=底面积×高
所以:圆柱体的体积=
底面积×高
V=
5. 一个圆柱形粮囤,从里面量得它的数据如右图所示,按每立方米稻谷重550kg计算,这个粮囤能装稻谷约多少吨?
容积:3.14××2.5
重量:
答:这个粮囤能装稻谷 吨。
V=
31.4×550=17270(kg)
17.27
=12.56×2.5
=31.4(m3)
基础练习
=17.27吨
6. 一个圆柱形无盖玻璃容器的底面半径是10cm,高是30cm。
(1)做这样一个容器至少要玻璃多少平方厘米?
(2)如果这个容器装的水深25cm,那么它装水多少毫升?
表=
侧面积:3.14×10×2×30=
底面积:3.14×102=
表面积:
答:至少要玻璃 平方厘米。
1884(cm2)
314(cm2)
1884+314=2198(cm2)
2198
V=
3.14×102×25
答:它装水 毫升。
=314×25
=7850(cm3)
=7850mL
7850
强化练习
7. 计算并填表。
①侧面积:3.14×5×2×5=
2个底面积:3.14×52×2=
表面积:
体积:
314cm2
54dm2
27dm3
213.52cm2
392.5cm3
157(cm2)
157+157=314(cm2)
3.14×52×5=392.5(cm3)
157(cm2)
②表面积:3×3×6=
体积:33=
54(dm2)
27(dm3)
③侧面积:3.14×4×15=
2个底面积:3.14×()2×2=
表面积:
体积:
188.4(cm2)
25.12(cm2)
188.4+25.12=213.52(cm2)
3.14×()2×15=188.4(cm3)
188.4cm3
S=6a2
=
V=
V=
8. 建筑工地输送混凝土的圆柱形管道内直径为10cm,混凝土在管道内的流速为每分 35m。一车混凝土有 7m3,多少分才能全部输送完?(用计算器计算,得数保留一位小数。)
10cm=
底面积:3.14×()2=
每分的体积(工效): ×35=
时间:
答: 分才能全部输送完。
作总量÷工作效率=工作时间
0.00785(m2)
0.00785
0.27475(m3)
0.1m
7÷0.27475≈25.5(分)
25.5
0.1
9. 削去部分的体积是多少立方厘米?
正方体的体积-圆柱体的体积=削去的体积
V正:9×9×9=
底面积:3.14×()2=
V圆: ×9=
V削:
答:削去部分的体积是 立方厘米。
729(cm3)
63.585(cm2)
63.585
572.265(cm3)
729-572.265=156.735(cm3)
156.735
10. 一根圆柱形钢管长4m,每立方厘米钢重7.8g,这根钢管重多少千克?
4m=400cm
体积:3.14×()2×400
重量:7.8× =
答:这根钢管重 千克。
=(3.14×400)×(62-42)
=1256×20
=25120(cm3)
25120
=195.936(kg)
h
-3.14×()2×400
195936(g)
195.936
10. 一根圆柱形钢管长4m,每立方厘米钢重7.8g,这根钢管重多少千克?
4m=400cm
底面积(内):3.14×()2=
体积(内): ×400=
底面积(外):3.14×()2=
体积(外): ×400=
体积(钢管):
重量:7.8× =
答:这根钢管重 千克。
50.24(cm2)
50.24
20096(cm3)
45216-20096=25120(cm3)
113.04(cm2)
113.04
45216(cm3)
25120
195936(g)
=195.936(kg)
195.936
思考题:把3个高相等,底面半径都是10cm的圆柱形盒子叠放在一起(如图),如果拿走1个盒子,表面积就要减少 314cm2。每个盒子的体积是多少立方厘米?
拿走1个盒子,减少一个盒子侧面积
底面周长:3.14×10×2=
高:314÷ =
底面积:3.14×102=
体积:
答:每个盒子的体积是 立方厘米。
62.8(cm)
5(cm)
314(cm2)
314×5=1570(cm3)
1570
62.8
课堂小结
这节课你们都学会了哪些知识?
★
★
★
=
=
课后作业
1.选择
(1)做一个圆柱形汽油桶,要用多少铁皮是求圆柱的( );
求汽油桶可装汽油多少升是求圆柱的( )。
A.侧面积 B.表面积 C.容积
(2)如果一个圆柱的侧面展开图是一个正方形,那么圆柱的
高是底面半径的( )倍。
A. B.2 C.3.14
圆柱的底面周长
圆柱的高
圆柱的底面周长=圆柱的高
= =2 r
r= ÷2÷
r= ÷(2× )
B
C
B
(3)小明打算用下面的长方形纸沿宽卷成一个圆柱的侧面,( )可以直接选作底面。(图中单位:cm)
12.56÷3.14÷2=
r= ÷ ÷2
A
2.判断。
(1)圆柱的底面积越大,体积越大。( )
(2)长方体、正方体和圆柱的体积都可以用底面积乘高的方法计算。( )
(3)表面积相等的两个圆柱,体积也相等。( )
×
√
×
(4)圆柱的底面半径缩小为原来的,高扩大到原来的2倍,体积不变。( )
(5)侧面积相等的两个圆柱的底面积一定相等。( )
×
半径×
体积××2
底面积×(
高×2
体积×
×
侧面积=底面周长×高,它们的乘积相等,并不代表底面周长相等。
3.一个容积为75.36L的圆柱形水桶,它的底面半径是2dm,高是多少分米
75.36L=75.36dm3
底面积:3.14×22=
高:7 =
答:高是 分米。
= r2
12.56(dm2)
12.56
6(dm)
6
4.把一个棱长为8 dm的正方体木块削成一个体积最大的圆柱,削去部分的体积是多少立方分米?
正方体的体积-圆柱体的体积=削去的体积
V正:8×8×8=
底面积:3.14×()2=
V圆: ×8=
V削:
答:削去部分的体积是 立方分米。
512(dm3)
50.24(dm2)
50.24
401.92(dm3)
512-401.92=110.08(dm3)
110.08
5.在一根内直径为8 cm的水管中,水流速度是每分250m,那么每分流过的水有多少立方米?
8cm=0.08m
底面积: 3.14×()2
体积: ×250=
答:每分流过的水有 立方米。
=3.14×0.042
=3.14×0.0016
=0.005024(m2)
0.005024
1.256(m3)
1.256
6.把3截底面直径都是20 cm的圆柱形木块叠放在一起(如下图),如果每添上1截,表面积就比原来增加942 cm 。每截木块的体积是多少立方厘米?
添上1截,增加一截的侧面积
底面周长:3.14×20=
高:942÷ =
底面积:3.14×(20÷2)2=
体积:
答:每个盒子的体积是 立方厘米。
62.8(cm)
15(cm)
314(cm2)
314×15=4710(cm3)
4710
62.8
圆柱的体积练习课
情境导入
基础练习
课堂小结
课后作业
圆柱和圆锥
强化练习
2
情境导入
长方体
圆柱
拼成的图形是近似的
把圆柱等分成16份
1.圆柱拼成近似的长方体后,它的形状变了吗
其体积发生变化了吗?
2.圆柱拼成近似的长方体后,它的底面积与高发生变化了吗?
高
底面积
高
=
底面积
=
因为:长方体的体积=底面积×高
所以:圆柱体的体积=
底面积×高
V=
5. 一个圆柱形粮囤,从里面量得它的数据如右图所示,按每立方米稻谷重550kg计算,这个粮囤能装稻谷约多少吨?
容积:3.14××2.5
重量:
答:这个粮囤能装稻谷 吨。
V=
31.4×550=17270(kg)
17.27
=12.56×2.5
=31.4(m3)
基础练习
=17.27吨
6. 一个圆柱形无盖玻璃容器的底面半径是10cm,高是30cm。
(1)做这样一个容器至少要玻璃多少平方厘米?
(2)如果这个容器装的水深25cm,那么它装水多少毫升?
表=
侧面积:3.14×10×2×30=
底面积:3.14×102=
表面积:
答:至少要玻璃 平方厘米。
1884(cm2)
314(cm2)
1884+314=2198(cm2)
2198
V=
3.14×102×25
答:它装水 毫升。
=314×25
=7850(cm3)
=7850mL
7850
强化练习
7. 计算并填表。
①侧面积:3.14×5×2×5=
2个底面积:3.14×52×2=
表面积:
体积:
314cm2
54dm2
27dm3
213.52cm2
392.5cm3
157(cm2)
157+157=314(cm2)
3.14×52×5=392.5(cm3)
157(cm2)
②表面积:3×3×6=
体积:33=
54(dm2)
27(dm3)
③侧面积:3.14×4×15=
2个底面积:3.14×()2×2=
表面积:
体积:
188.4(cm2)
25.12(cm2)
188.4+25.12=213.52(cm2)
3.14×()2×15=188.4(cm3)
188.4cm3
S=6a2
=
V=
V=
8. 建筑工地输送混凝土的圆柱形管道内直径为10cm,混凝土在管道内的流速为每分 35m。一车混凝土有 7m3,多少分才能全部输送完?(用计算器计算,得数保留一位小数。)
10cm=
底面积:3.14×()2=
每分的体积(工效): ×35=
时间:
答: 分才能全部输送完。
作总量÷工作效率=工作时间
0.00785(m2)
0.00785
0.27475(m3)
0.1m
7÷0.27475≈25.5(分)
25.5
0.1
9. 削去部分的体积是多少立方厘米?
正方体的体积-圆柱体的体积=削去的体积
V正:9×9×9=
底面积:3.14×()2=
V圆: ×9=
V削:
答:削去部分的体积是 立方厘米。
729(cm3)
63.585(cm2)
63.585
572.265(cm3)
729-572.265=156.735(cm3)
156.735
10. 一根圆柱形钢管长4m,每立方厘米钢重7.8g,这根钢管重多少千克?
4m=400cm
体积:3.14×()2×400
重量:7.8× =
答:这根钢管重 千克。
=(3.14×400)×(62-42)
=1256×20
=25120(cm3)
25120
=195.936(kg)
h
-3.14×()2×400
195936(g)
195.936
10. 一根圆柱形钢管长4m,每立方厘米钢重7.8g,这根钢管重多少千克?
4m=400cm
底面积(内):3.14×()2=
体积(内): ×400=
底面积(外):3.14×()2=
体积(外): ×400=
体积(钢管):
重量:7.8× =
答:这根钢管重 千克。
50.24(cm2)
50.24
20096(cm3)
45216-20096=25120(cm3)
113.04(cm2)
113.04
45216(cm3)
25120
195936(g)
=195.936(kg)
195.936
思考题:把3个高相等,底面半径都是10cm的圆柱形盒子叠放在一起(如图),如果拿走1个盒子,表面积就要减少 314cm2。每个盒子的体积是多少立方厘米?
拿走1个盒子,减少一个盒子侧面积
底面周长:3.14×10×2=
高:314÷ =
底面积:3.14×102=
体积:
答:每个盒子的体积是 立方厘米。
62.8(cm)
5(cm)
314(cm2)
314×5=1570(cm3)
1570
62.8
课堂小结
这节课你们都学会了哪些知识?
★
★
★
=
=
课后作业
1.选择
(1)做一个圆柱形汽油桶,要用多少铁皮是求圆柱的( );
求汽油桶可装汽油多少升是求圆柱的( )。
A.侧面积 B.表面积 C.容积
(2)如果一个圆柱的侧面展开图是一个正方形,那么圆柱的
高是底面半径的( )倍。
A. B.2 C.3.14
圆柱的底面周长
圆柱的高
圆柱的底面周长=圆柱的高
= =2 r
r= ÷2÷
r= ÷(2× )
B
C
B
(3)小明打算用下面的长方形纸沿宽卷成一个圆柱的侧面,( )可以直接选作底面。(图中单位:cm)
12.56÷3.14÷2=
r= ÷ ÷2
A
2.判断。
(1)圆柱的底面积越大,体积越大。( )
(2)长方体、正方体和圆柱的体积都可以用底面积乘高的方法计算。( )
(3)表面积相等的两个圆柱,体积也相等。( )
×
√
×
(4)圆柱的底面半径缩小为原来的,高扩大到原来的2倍,体积不变。( )
(5)侧面积相等的两个圆柱的底面积一定相等。( )
×
半径×
体积××2
底面积×(
高×2
体积×
×
侧面积=底面周长×高,它们的乘积相等,并不代表底面周长相等。
3.一个容积为75.36L的圆柱形水桶,它的底面半径是2dm,高是多少分米
75.36L=75.36dm3
底面积:3.14×22=
高:7 =
答:高是 分米。
= r2
12.56(dm2)
12.56
6(dm)
6
4.把一个棱长为8 dm的正方体木块削成一个体积最大的圆柱,削去部分的体积是多少立方分米?
正方体的体积-圆柱体的体积=削去的体积
V正:8×8×8=
底面积:3.14×()2=
V圆: ×8=
V削:
答:削去部分的体积是 立方分米。
512(dm3)
50.24(dm2)
50.24
401.92(dm3)
512-401.92=110.08(dm3)
110.08
5.在一根内直径为8 cm的水管中,水流速度是每分250m,那么每分流过的水有多少立方米?
8cm=0.08m
底面积: 3.14×()2
体积: ×250=
答:每分流过的水有 立方米。
=3.14×0.042
=3.14×0.0016
=0.005024(m2)
0.005024
1.256(m3)
1.256
6.把3截底面直径都是20 cm的圆柱形木块叠放在一起(如下图),如果每添上1截,表面积就比原来增加942 cm 。每截木块的体积是多少立方厘米?
添上1截,增加一截的侧面积
底面周长:3.14×20=
高:942÷ =
底面积:3.14×(20÷2)2=
体积:
答:每个盒子的体积是 立方厘米。
62.8(cm)
15(cm)
314(cm2)
314×15=4710(cm3)
4710
62.8
