第六章 圆周运动 单元测试(word版含答案)
文档属性
| 名称 | 第六章 圆周运动 单元测试(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 253.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-03 07:26:21 | ||
图片预览




文档简介
人教版高一物理第六章圆周运动单元测试
一、单选题(本大题共10小题,共40.0分)
物体做匀速圆周运动的过程中,不发生变化的物理量是
A. 合力 B. 线速度 C. 向心加速度 D. 周期
关于做匀速圆周运动的物体,下列说法正确的是
A. 因为在相等的时间内通过的圆弧长度相等,所以线速度恒定
B. 如果物体在内转过角,则角速度为
C. 若半径一定,则线速度与角速度成反比
D. 匀速圆周运动是变加速曲线运动
一质点做匀速圆周运动,其线速度为,转速为,下列说法中正确的是
A. 该质点做匀速圆周运动的角速度为
B. 该质点做匀速圆周运动的半径为
C. 该质点做匀速圆周运动的加速度大小为
D. 匀速圆周运动是一种加速度不变的运动
如图所示的皮带传动装置中,轮和同轴,、、分别是三个轮边缘的质点,且,则下列说法中正确的是
A. 三质点的线速度之比
B. 三质点的角速度之比
C. 三质点的周期之比
D. 三质点的转速之比
如图所示的四幅图表示的是有关圆周运动的基本模型,下列说法正确的是:
A. 如图,汽车通过拱桥的最高点时处于失重状态
B. 图所示是一圆锥摆,增大,但保持圆锥的高度不变,则圆锥摆的角速度减小
C. 如图,同一小球在光滑而固定的圆锥筒内的、位置先后做匀速圆周运动,则在、两位置小球的角速度及所受筒壁的支持力大小均相等
D. 如图,火车转弯超过规定速度行驶时,内轨对内轮缘会有挤压作用
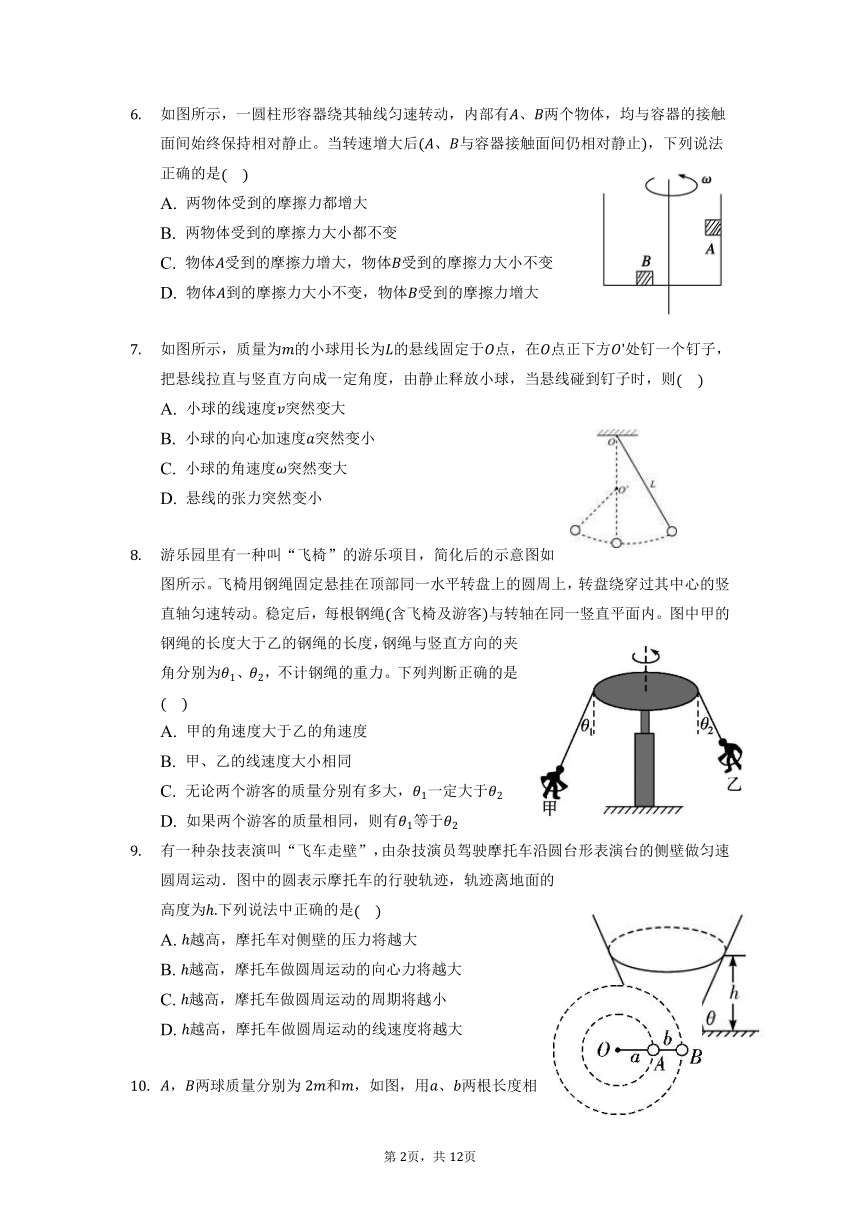
如图所示,一圆柱形容器绕其轴线匀速转动,内部有、两个物体,均与容器的接触面间始终保持相对静止。当转速增大后、与容器接触面间仍相对静止,下列说法正确的是
A. 两物体受到的摩擦力都增大
B. 两物体受到的摩擦力大小都不变
C. 物体受到的摩擦力增大,物体受到的摩擦力大小不变
D. 物体到的摩擦力大小不变,物体受到的摩擦力增大
如图所示,质量为的小球用长为的悬线固定于点,在点正下方处钉一个钉子,把悬线拉直与竖直方向成一定角度,由静止释放小球,当悬线碰到钉子时,则
A. 小球的线速度突然变大
B. 小球的向心加速度突然变小
C. 小球的角速度突然变大
D. 悬线的张力突然变小
游乐园里有一种叫“飞椅”的游乐项目,简化后的示意图如图所示。飞椅用钢绳固定悬挂在顶部同一水平转盘上的圆周上,转盘绕穿过其中心的竖直轴匀速转动。稳定后,每根钢绳含飞椅及游客与转轴在同一竖直平面内。图中甲的钢绳的长度大于乙的钢绳的长度,钢绳与竖直方向的夹角分别为、,不计钢绳的重力。下列判断正确的是
A. 甲的角速度大于乙的角速度
B. 甲、乙的线速度大小相同
C. 无论两个游客的质量分别有多大,一定大于
D. 如果两个游客的质量相同,则有等于
有一种杂技表演叫“飞车走壁”,由杂技演员驾驶摩托车沿圆台形表演台的侧壁做匀速圆周运动.图中的圆表示摩托车的行驶轨迹,轨迹离地面的高度为下列说法中正确的是
A. 越高,摩托车对侧壁的压力将越大
B. 越高,摩托车做圆周运动的向心力将越大
C. 越高,摩托车做圆周运动的周期将越小
D. 越高,摩托车做圆周运动的线速度将越大
,两球质量分别为和,如图,用、两根长度相同的绳系住,绕绳的端在光滑水平面上以相同角速度做匀速圆周运动,则、两根绳张力大小之比为
A. B.
C. D.
二、实验题(本大题共2小题,共18.0分)
用如图所示的装置来探究小球做圆周运动所需向心力的大小与质量、角速度和半径之间的关系.两个变速轮塔通过皮带连接,转动手柄使长槽和短槽分别随变速轮塔匀速转动,槽内的钢球就做匀速圆周运动.横臂的挡板对钢球的压力提供向心力,钢球对挡板的反作用力通过横臂的杠杆作用使弹簧测力筒下降,从而露出标尺,标尺上的红白相间的等分格显示出两个钢球所受向心力的比值.如图是探究过程中某次实验时装置的状态.
本实验采用的科学方法是______
A.控制变量法 累积法 微元法 放大法
图中所示是在研究向心力的大小与______的关系.
A.质量 半径 角速度
电动平衡车,又叫体感车、思维车、摄位车等,是现代人用来作为代步工具、休闲娱乐的一种新型的绿色环保的产物.两轮电动平衡车采用两个轮子支撑,蓄电池供电,无刷电机驱动,加上单片机控制,姿态传感器采集角速度和角度信号,共同协调控制车体的平衡,仅仅依靠人体重心的改变便可以实现车辆的启动、加速、减速、停止等动作.
某学校物理兴趣小组的同学学习了圆周运动知识后,想到可以使用学到的知识测量平衡车的速度并进行相关实验,他们带着一辆车轮半径为的平衡车和一辆车轮半径为的自行车到了学校操场上,在平衡车车轮和自行车车轮上固定可测量圈数的传感器。
第一次实验,同学驾驶平衡车在操场跑道上做匀速直线运动,其他同学测出了在的时间内平衡车车轮转过的圈数为,则平衡车车轮的角速度为______.
第二次实验,同学驾驶平衡车,同学骑自行车,都匀速骑行,在相同时间内平衡车转过的圈数是自行车转过的圈数的三倍,则平衡车与自行车前进速度大小之比为______.
第三次实验,同学驾驶平衡车,同学骑自行车,两同学同时从百米跑道起点出发,又同时到达百米终点,则平衡车与自行车车轮边缘上平均向心加速度大小之比为______.
三、计算题(本大题共3小题,共42.0分)
如下图所示,装置可绕竖直轴转动,可视为质点的小球与两细线连接后分别系于、两点,装置静止时细线水平,细线与竖直方向的夹角为已知小球的质量,细线长,点距点的水平和竖直距离相等.重力加速度取
若装置匀速转动的角速度为,细线上的张力为零而细线与竖直方向的夹角仍为,求角速度的大小.
若装置匀速转动的角速度求细线的张力.
装置可以以不同的角速度匀速转动,试通过计算,写出细线上张力随角速度的平方变化的关系式.
如图所示,长为的绳子质量不计下端连着质量为的小球,上端悬于天花板上,当把绳子恰好拉直时,绳子与竖直线的夹角,此时小球静止于光滑的水平桌面上.
当球以做圆锥摆运动时,绳子张力为多大桌面受到的压力为多大
当球以角速度做圆锥摆运动时,绳子的张力及桌面受到的压力分别为多少
如图所示,细绳一端系着质量的物体,另一端通过圆盘中心的光滑小孔吊着质量的物体,物体与小孔距离为物体可看成质点,已知和水平圆盘间的最大静摩擦力为,重力加速度。
若圆盘静止不动,从静止释放,求的加速度大小;
若使圆盘绕中心轴线转动,处于静止状态,求角速度的最大值。
答案和解析
1.【答案】
【解答】
在描述匀速圆周运动的物理量中,合力、向心加速度、线速度这几个物理量都是矢量,虽然其大小不变但是方向在变,因此这些物理量是变化的,周期是标量,是不变化的,故ABC错误,D正确。
故选D
2.【答案】
【解答】
A.因相等时间内通过的弧长相等,所以线速度大小不变,但是方向时刻变化,故A错误;
B.根据,故B错误;
C.线速度与角速度的关系为,由该式可知,一定时,,故C错误;
D.做匀速圆周运动的物体加速度大小恒定方向变化,为变加速曲线运动,故D正确。
故选D。
3.【答案】
4.【答案】
【解析】由于轮和轮是皮带传动,皮带传动的特点是两轮与皮带接触点的线速度的大小与皮带的线速度大小相同,
故::,
由于轮和轮共轴,故两轮角速度相同, 故::,
由角速度和线速度的关系式可得
:::,
:::,
则有:
A.线速度之比为:::::,故A正确;
B.角速度之比为::::,故B错误;
C.根据得:::::,故C错误;
D. 转速,故转速之比等于角速度之比为:::;故D错误;
故选A。
5.【答案】
【解答】
A.汽车通过拱桥的最高点时,加速度方向向下,处于失重状态,故A正确;
B.图是圆锥摆,重力和绳子的拉力充当向心力,故有,设圆锥的高度为,则运动半径为,故有,解得,角速度大小与角度无关,故B错误;
C.在两个位置上小球的重力相同,支持力方向相同,所以合力相同,即向心力相同,根据公式可得半径越大,角速度越小,故角速度不同,所受筒壁的支持力大小相等,故C错误;
D.当火车在规定的速度转弯时,由支持力与重力的合力提供火车转弯所需的向心力,当速度大于规定的速度时,火车的支持力与重力的合力不足以提供火车所需的向心力,外轨对轮缘有挤压作用,火车轮缘挤压外轨,故D错误。
故选A。
6.【答案】
容器绕其轴线转动时,两个物体随容器一起转动,以为研究对象,在水平方向上,容器施加的弹力提供做圆周运动的向心力;在竖直方向,重力和静摩擦力平衡,所以当转速增大后,物体受到的摩擦力大小的保持不变;
以为研究对象,水平方向的静摩擦力提供向心力,由得,其受到的静摩擦力随着转速的增大而增大,故ABC错误D正确。
故选D。
7.【答案】
【解答】
A.当悬线碰到钉子时,线速度大小不变,故A错误;
B.当悬线碰到钉子时,线速度大小不变,摆长变小,即半径变小,根据知,向心加速度变大,故B错误;
C.线速度大小不变,摆长变小,根据知,角速度变大,故C正确;
D.根据牛顿第二定律得,,向心加速度变大,则悬线的张力变大,故D错误。
故选C。
8.【答案】
【解答】
同轴转动角速度相同,由可知半径不同线速度不同,则,则AB错误;
重力与拉力的合力为,由,其中为圆盘半径,解得:,得,越小则越小。则,与质量无关,则C正确,D错误。
9.【答案】
【解答】摩托车沿圆台形表演台的侧壁做匀速圆周运动时的向心力由摩托车的重力和侧壁的支持力的合力提供,支持力 ,向心力,可见,和只与侧壁的倾角有关,而与高度无关,即变化时,和不变,、B错误;
D.根据,可得,当越高时,轨道半径越大,所以线速度越大,D正确;
C.根据,,可得 ,当越高时,轨道半径越大,周期越大,C错误.
10.【答案】
设
对球有:。
对球有:。
联立两式解得:故D正确,ABC错误。
故选D。
11.【答案】;
【解答】
在研究向心力的大小与质量、角速度和半径之间的关系时,需先控制某些量不变,研究另外两个物理量的关系,该方法为控制变量法,故选A;
图中两球的质量相同,转动的半径相同,则研究的是向心力与角速度的关系,故选C。
故答案为:;。
12.【答案】
【解答】
根据角速度,得:
自行车的角速度,;根据;故速度之比:;
;故线速度相等,根据;::;平均向心加速度。
故答案为:
13.【答案】解:当细线上的张力为零时,小球的重力和细线张力的合力提供小球做圆周运动的向心力,有,代入数据解得: 。
当时,因为 ,
小球应该向左上方摆起,假设细线上的张力仍然为零,设细线的弹力为,则
对小球进行受力分析有:
,解得
代入数据解得:,
因为点距点的水平和竖直距离相等,所以,当时,细线恰好竖直,且:
说明细线此时的张力为零,故此时细线与竖直方向的夹角为。
时,细线水平,细线上的张力的竖直分量等于小球的重力,即:,则:
时,细线松弛,细线上张力的水平分量等于小球做圆周运动需要的向心力,,则:
时,细线在竖直方向绷直,仍由细线上张力的水平分量提供小球做圆周运动需要的向心力。
,则:
综上所述: 时, 不变;时,。
答:角速度的大小为 ;
若装置匀速转动的角速度,细线的弹力为,细线与竖直方向的夹角为;
当 时, 不变;时,。
14.【答案】解:对小球受力分析如图,
球在水平面内做匀速圆周运动,由重力、水平面的支持力和绳子拉力的合力提供向心力,则根据牛顿第二定律,得
水平方向有:
竖直方向有:
又
解得,
根据牛顿第三定律得知桌面受到的压力;
设小球对桌面恰好无压力时角速度为,
水平方向有:
竖直方向有:
联立解得,
由于,故小球离开桌面做匀速圆周运动,即桌面受到的压力,由绳子的拉力与球的重力的合力提供向心力
设绳子与竖直方向的夹角为,则有
联立解得
15.【答案】解:对,根据牛顿第二定律得:
,
对,根据牛顿第二定律得:
解得:
当具有最大值时,有离开圆心运动的趋势,受的最大静摩擦力指向圆心,对受力分析有:
,
又,
解得 。
第2页,共2页
一、单选题(本大题共10小题,共40.0分)
物体做匀速圆周运动的过程中,不发生变化的物理量是
A. 合力 B. 线速度 C. 向心加速度 D. 周期
关于做匀速圆周运动的物体,下列说法正确的是
A. 因为在相等的时间内通过的圆弧长度相等,所以线速度恒定
B. 如果物体在内转过角,则角速度为
C. 若半径一定,则线速度与角速度成反比
D. 匀速圆周运动是变加速曲线运动
一质点做匀速圆周运动,其线速度为,转速为,下列说法中正确的是
A. 该质点做匀速圆周运动的角速度为
B. 该质点做匀速圆周运动的半径为
C. 该质点做匀速圆周运动的加速度大小为
D. 匀速圆周运动是一种加速度不变的运动
如图所示的皮带传动装置中,轮和同轴,、、分别是三个轮边缘的质点,且,则下列说法中正确的是
A. 三质点的线速度之比
B. 三质点的角速度之比
C. 三质点的周期之比
D. 三质点的转速之比
如图所示的四幅图表示的是有关圆周运动的基本模型,下列说法正确的是:
A. 如图,汽车通过拱桥的最高点时处于失重状态
B. 图所示是一圆锥摆,增大,但保持圆锥的高度不变,则圆锥摆的角速度减小
C. 如图,同一小球在光滑而固定的圆锥筒内的、位置先后做匀速圆周运动,则在、两位置小球的角速度及所受筒壁的支持力大小均相等
D. 如图,火车转弯超过规定速度行驶时,内轨对内轮缘会有挤压作用
如图所示,一圆柱形容器绕其轴线匀速转动,内部有、两个物体,均与容器的接触面间始终保持相对静止。当转速增大后、与容器接触面间仍相对静止,下列说法正确的是
A. 两物体受到的摩擦力都增大
B. 两物体受到的摩擦力大小都不变
C. 物体受到的摩擦力增大,物体受到的摩擦力大小不变
D. 物体到的摩擦力大小不变,物体受到的摩擦力增大
如图所示,质量为的小球用长为的悬线固定于点,在点正下方处钉一个钉子,把悬线拉直与竖直方向成一定角度,由静止释放小球,当悬线碰到钉子时,则
A. 小球的线速度突然变大
B. 小球的向心加速度突然变小
C. 小球的角速度突然变大
D. 悬线的张力突然变小
游乐园里有一种叫“飞椅”的游乐项目,简化后的示意图如图所示。飞椅用钢绳固定悬挂在顶部同一水平转盘上的圆周上,转盘绕穿过其中心的竖直轴匀速转动。稳定后,每根钢绳含飞椅及游客与转轴在同一竖直平面内。图中甲的钢绳的长度大于乙的钢绳的长度,钢绳与竖直方向的夹角分别为、,不计钢绳的重力。下列判断正确的是
A. 甲的角速度大于乙的角速度
B. 甲、乙的线速度大小相同
C. 无论两个游客的质量分别有多大,一定大于
D. 如果两个游客的质量相同,则有等于
有一种杂技表演叫“飞车走壁”,由杂技演员驾驶摩托车沿圆台形表演台的侧壁做匀速圆周运动.图中的圆表示摩托车的行驶轨迹,轨迹离地面的高度为下列说法中正确的是
A. 越高,摩托车对侧壁的压力将越大
B. 越高,摩托车做圆周运动的向心力将越大
C. 越高,摩托车做圆周运动的周期将越小
D. 越高,摩托车做圆周运动的线速度将越大
,两球质量分别为和,如图,用、两根长度相同的绳系住,绕绳的端在光滑水平面上以相同角速度做匀速圆周运动,则、两根绳张力大小之比为
A. B.
C. D.
二、实验题(本大题共2小题,共18.0分)
用如图所示的装置来探究小球做圆周运动所需向心力的大小与质量、角速度和半径之间的关系.两个变速轮塔通过皮带连接,转动手柄使长槽和短槽分别随变速轮塔匀速转动,槽内的钢球就做匀速圆周运动.横臂的挡板对钢球的压力提供向心力,钢球对挡板的反作用力通过横臂的杠杆作用使弹簧测力筒下降,从而露出标尺,标尺上的红白相间的等分格显示出两个钢球所受向心力的比值.如图是探究过程中某次实验时装置的状态.
本实验采用的科学方法是______
A.控制变量法 累积法 微元法 放大法
图中所示是在研究向心力的大小与______的关系.
A.质量 半径 角速度
电动平衡车,又叫体感车、思维车、摄位车等,是现代人用来作为代步工具、休闲娱乐的一种新型的绿色环保的产物.两轮电动平衡车采用两个轮子支撑,蓄电池供电,无刷电机驱动,加上单片机控制,姿态传感器采集角速度和角度信号,共同协调控制车体的平衡,仅仅依靠人体重心的改变便可以实现车辆的启动、加速、减速、停止等动作.
某学校物理兴趣小组的同学学习了圆周运动知识后,想到可以使用学到的知识测量平衡车的速度并进行相关实验,他们带着一辆车轮半径为的平衡车和一辆车轮半径为的自行车到了学校操场上,在平衡车车轮和自行车车轮上固定可测量圈数的传感器。
第一次实验,同学驾驶平衡车在操场跑道上做匀速直线运动,其他同学测出了在的时间内平衡车车轮转过的圈数为,则平衡车车轮的角速度为______.
第二次实验,同学驾驶平衡车,同学骑自行车,都匀速骑行,在相同时间内平衡车转过的圈数是自行车转过的圈数的三倍,则平衡车与自行车前进速度大小之比为______.
第三次实验,同学驾驶平衡车,同学骑自行车,两同学同时从百米跑道起点出发,又同时到达百米终点,则平衡车与自行车车轮边缘上平均向心加速度大小之比为______.
三、计算题(本大题共3小题,共42.0分)
如下图所示,装置可绕竖直轴转动,可视为质点的小球与两细线连接后分别系于、两点,装置静止时细线水平,细线与竖直方向的夹角为已知小球的质量,细线长,点距点的水平和竖直距离相等.重力加速度取
若装置匀速转动的角速度为,细线上的张力为零而细线与竖直方向的夹角仍为,求角速度的大小.
若装置匀速转动的角速度求细线的张力.
装置可以以不同的角速度匀速转动,试通过计算,写出细线上张力随角速度的平方变化的关系式.
如图所示,长为的绳子质量不计下端连着质量为的小球,上端悬于天花板上,当把绳子恰好拉直时,绳子与竖直线的夹角,此时小球静止于光滑的水平桌面上.
当球以做圆锥摆运动时,绳子张力为多大桌面受到的压力为多大
当球以角速度做圆锥摆运动时,绳子的张力及桌面受到的压力分别为多少
如图所示,细绳一端系着质量的物体,另一端通过圆盘中心的光滑小孔吊着质量的物体,物体与小孔距离为物体可看成质点,已知和水平圆盘间的最大静摩擦力为,重力加速度。
若圆盘静止不动,从静止释放,求的加速度大小;
若使圆盘绕中心轴线转动,处于静止状态,求角速度的最大值。
答案和解析
1.【答案】
【解答】
在描述匀速圆周运动的物理量中,合力、向心加速度、线速度这几个物理量都是矢量,虽然其大小不变但是方向在变,因此这些物理量是变化的,周期是标量,是不变化的,故ABC错误,D正确。
故选D
2.【答案】
【解答】
A.因相等时间内通过的弧长相等,所以线速度大小不变,但是方向时刻变化,故A错误;
B.根据,故B错误;
C.线速度与角速度的关系为,由该式可知,一定时,,故C错误;
D.做匀速圆周运动的物体加速度大小恒定方向变化,为变加速曲线运动,故D正确。
故选D。
3.【答案】
4.【答案】
【解析】由于轮和轮是皮带传动,皮带传动的特点是两轮与皮带接触点的线速度的大小与皮带的线速度大小相同,
故::,
由于轮和轮共轴,故两轮角速度相同, 故::,
由角速度和线速度的关系式可得
:::,
:::,
则有:
A.线速度之比为:::::,故A正确;
B.角速度之比为::::,故B错误;
C.根据得:::::,故C错误;
D. 转速,故转速之比等于角速度之比为:::;故D错误;
故选A。
5.【答案】
【解答】
A.汽车通过拱桥的最高点时,加速度方向向下,处于失重状态,故A正确;
B.图是圆锥摆,重力和绳子的拉力充当向心力,故有,设圆锥的高度为,则运动半径为,故有,解得,角速度大小与角度无关,故B错误;
C.在两个位置上小球的重力相同,支持力方向相同,所以合力相同,即向心力相同,根据公式可得半径越大,角速度越小,故角速度不同,所受筒壁的支持力大小相等,故C错误;
D.当火车在规定的速度转弯时,由支持力与重力的合力提供火车转弯所需的向心力,当速度大于规定的速度时,火车的支持力与重力的合力不足以提供火车所需的向心力,外轨对轮缘有挤压作用,火车轮缘挤压外轨,故D错误。
故选A。
6.【答案】
容器绕其轴线转动时,两个物体随容器一起转动,以为研究对象,在水平方向上,容器施加的弹力提供做圆周运动的向心力;在竖直方向,重力和静摩擦力平衡,所以当转速增大后,物体受到的摩擦力大小的保持不变;
以为研究对象,水平方向的静摩擦力提供向心力,由得,其受到的静摩擦力随着转速的增大而增大,故ABC错误D正确。
故选D。
7.【答案】
【解答】
A.当悬线碰到钉子时,线速度大小不变,故A错误;
B.当悬线碰到钉子时,线速度大小不变,摆长变小,即半径变小,根据知,向心加速度变大,故B错误;
C.线速度大小不变,摆长变小,根据知,角速度变大,故C正确;
D.根据牛顿第二定律得,,向心加速度变大,则悬线的张力变大,故D错误。
故选C。
8.【答案】
【解答】
同轴转动角速度相同,由可知半径不同线速度不同,则,则AB错误;
重力与拉力的合力为,由,其中为圆盘半径,解得:,得,越小则越小。则,与质量无关,则C正确,D错误。
9.【答案】
【解答】摩托车沿圆台形表演台的侧壁做匀速圆周运动时的向心力由摩托车的重力和侧壁的支持力的合力提供,支持力 ,向心力,可见,和只与侧壁的倾角有关,而与高度无关,即变化时,和不变,、B错误;
D.根据,可得,当越高时,轨道半径越大,所以线速度越大,D正确;
C.根据,,可得 ,当越高时,轨道半径越大,周期越大,C错误.
10.【答案】
设
对球有:。
对球有:。
联立两式解得:故D正确,ABC错误。
故选D。
11.【答案】;
【解答】
在研究向心力的大小与质量、角速度和半径之间的关系时,需先控制某些量不变,研究另外两个物理量的关系,该方法为控制变量法,故选A;
图中两球的质量相同,转动的半径相同,则研究的是向心力与角速度的关系,故选C。
故答案为:;。
12.【答案】
【解答】
根据角速度,得:
自行车的角速度,;根据;故速度之比:;
;故线速度相等,根据;::;平均向心加速度。
故答案为:
13.【答案】解:当细线上的张力为零时,小球的重力和细线张力的合力提供小球做圆周运动的向心力,有,代入数据解得: 。
当时,因为 ,
小球应该向左上方摆起,假设细线上的张力仍然为零,设细线的弹力为,则
对小球进行受力分析有:
,解得
代入数据解得:,
因为点距点的水平和竖直距离相等,所以,当时,细线恰好竖直,且:
说明细线此时的张力为零,故此时细线与竖直方向的夹角为。
时,细线水平,细线上的张力的竖直分量等于小球的重力,即:,则:
时,细线松弛,细线上张力的水平分量等于小球做圆周运动需要的向心力,,则:
时,细线在竖直方向绷直,仍由细线上张力的水平分量提供小球做圆周运动需要的向心力。
,则:
综上所述: 时, 不变;时,。
答:角速度的大小为 ;
若装置匀速转动的角速度,细线的弹力为,细线与竖直方向的夹角为;
当 时, 不变;时,。
14.【答案】解:对小球受力分析如图,
球在水平面内做匀速圆周运动,由重力、水平面的支持力和绳子拉力的合力提供向心力,则根据牛顿第二定律,得
水平方向有:
竖直方向有:
又
解得,
根据牛顿第三定律得知桌面受到的压力;
设小球对桌面恰好无压力时角速度为,
水平方向有:
竖直方向有:
联立解得,
由于,故小球离开桌面做匀速圆周运动,即桌面受到的压力,由绳子的拉力与球的重力的合力提供向心力
设绳子与竖直方向的夹角为,则有
联立解得
15.【答案】解:对,根据牛顿第二定律得:
,
对,根据牛顿第二定律得:
解得:
当具有最大值时,有离开圆心运动的趋势,受的最大静摩擦力指向圆心,对受力分析有:
,
又,
解得 。
第2页,共2页
