小学数学苏教版四年级下7.6三角形练习 教案
文档属性
| 名称 | 小学数学苏教版四年级下7.6三角形练习 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 537.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-03 09:46:36 | ||
图片预览


文档简介
三角形练习
【教学内容】
苏教版义务教育教科书《数学》四年级下册第86~87页练习十三第7~14题。
【教学目标】
1.使学生进一步认识三角形,巩固三角形边的关系、内角和、三角形分类的有关知识,能应用三角形的知识解决相关问题。
2.使学生在应用知识进行判断、推理和解决问题等活动中,提高分析、判断、推理等思维能力,进一步体会分类、演绎等数学思想方法,感受解决问题方法的多样,发展空间观念。
3.使学生了解三角形的丰富内容,获得应用知识的成功体验,产生对数学知识的兴趣,提高学习数学的自信心和积极性。
【教学重点】
学会三角形知识的应用。
【教学难点】
应用知识分析推理和解释。
【教学准备】
几何画板课件、PPT课件、学习单
【教学过程】
一、知识整理
1.回顾内容。
引导:孩子们,课前我们通过学习单上的理学,对最近学习的三角形的知识进行了简单的复习,本节课我们先来把这些知识一起整理整理。
2.复习三角形基本特征。
(1)复习三个顶点。
提问:你知道怎样的图形是三角形吗?(板书:三条线段首尾相接围成的图形)
三角形有什么特征?(板书:3个顶点、3条边和3个角,稳定性。)
出示:出示几何画板A、B两点。
提问:这是A、B两点,可以连成一条线段,现在要找第三个点C,连成三角形,那么对第三个点有没有什么要求?(板书:不在同一直线上)
出示:出示几何画板。
(2)复习三边关系。
提问:对于三角形的三边关系,你掌握了什么?(板书:任意两边之和大于第三边)
出示:几何画板三角形三边关系数据。
说明:这是一个一般三角形,两边之和大于第三边,不管怎么改变,任意两边之和始终大于第三边。
引导:移动一个顶点,仔细看这组数据,你想说什么?(当两边之和等于第三边,不能围成三角形。)
(3)复习三角形内角和。
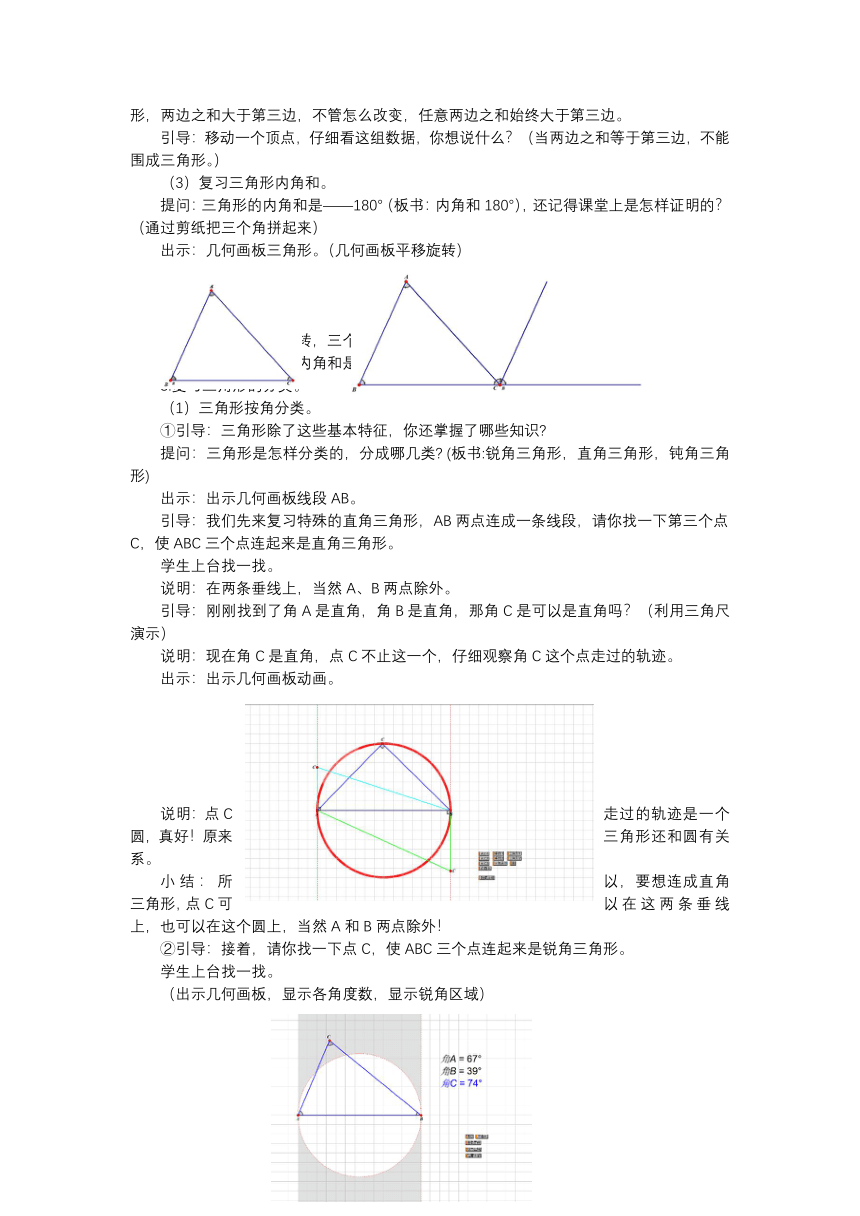
提问:三角形的内角和是——180°(板书:内角和180°),还记得课堂上是怎样证明的?(通过剪纸把三个角拼起来)
出示:几何画板三角形。(几何画板平移旋转)
引导:经过平移和旋转,三个角拼起来是什么?(拼成了一个平角)
追问:所以三角形的内角和是?(180°。)
3.复习三角形的分类。
(1)三角形按角分类。
①引导:三角形除了这些基本特征,你还掌握了哪些知识
提问:三角形是怎样分类的,分成哪几类 (板书:锐角三角形,直角三角形,钝角三角形)
出示:出示几何画板线段AB。
引导:我们先来复习特殊的直角三角形,AB两点连成一条线段,请你找一下第三个点C,使ABC三个点连起来是直角三角形。
学生上台找一找。
说明:在两条垂线上,当然A、B两点除外。
引导:刚刚找到了角A是直角,角B是直角,那角C是可以是直角吗?(利用三角尺演示)
说明:现在角C是直角,点C不止这一个,仔细观察角C这个点走过的轨迹。
出示:出示几何画板动画。
说明:点C走过的轨迹是一个圆,真好!原来三角形还和圆有关系。
小结:所以,要想连成直角三角形,点C可以在这两条垂线上,也可以在这个圆上,当然A和B两点除外!
②引导:接着,请你找一下点C,使ABC三个点连起来是锐角三角形。
学生上台找一找。
(出示几何画板,显示各角度数,显示锐角区域)
③引导:最后,请你找一下点C,使ABC三个点连起来是钝角三角形。
学生上台找一找,说明钝角区域。
(2)三角形按边分类。
引导:刚刚我们复习了三角形按角分类。那三角形还可以——按边分类。
说明:特殊的等腰三角形和等边三角形,其他的三条边都不等的叫做一般三角形。
追问:一般三角形指什么?
出示:出示几何画板线段AB。
引导:以线段AB为底,请你找第三个点C,使三角形ABC是一个等腰三角形。
学生上台指一指。
(预设:在对称轴上。说明:等腰三角形是轴对称图形)
出示:几何画板连接三角形,出示三角形各边长,两边相等。
出示:几何画板出示角度,底角相等。
说明:等腰三角形两边相等,底角相等。
引导:(几何画板改变形状)不管我怎么改变三角形的形状,它始终是一个等腰三角形。
提问:我们说等边三角形是特殊的等腰三角形,那么点C移动到哪里时,三角形会是一个等边三角形?
学生上台指一指。
演示:我移动,你们说停我就停。
提问:为什么现在叫我停了?
(三条边都相等时,也就是当等腰三角形的腰和底相等时,就是一个等边三角形。)
追问:仔细看看,你还有什么发现?(三个角都是60°。)
追问:只有这一个点C吗?(下面还有一个)
(3)集合圈
引导:孩子们,你们掌握的真好,按角分类,如果用一个圈来表示所有的三角形的家,那锐角、直角、钝角三角形应该住在哪?
学生黑板移一移。
引导:按边分类,如果用一个圈来表示所有的三角形的家,它们住在哪?
学生黑板移一移。
二、巩固练习
引入:知识需要巩固和应用,下面我们一起来练习三角形的内容,看看每题都用到了什么知识。(板书:用到了什么知识?)
1.练习十三第7题(变式)。
(1)题目:判断下面各是什么三角形。
学生判断,说出理由。
提问:仔细观察第二个直角三角形,你还发现什么?
说明:两条边相等,它也是一个等腰三角形,合起来它就是等腰直角三角形。
(2)题目:画出下面三角形底边上的高。
交流:什么是三角形的高?画高要注意什么?
学生投影展示(钝角三角形画高),有错纠正,同桌检查。
提问:观察三条高的位置,你有什么发现?(三角形的高可能在三角形的里面,可能在三角形的边上,可能在三角形的外面。)
小结:这题解决了,用到了什么知识?
2.练习十三第8题。
题目:下面的三角形都被一张纸遮住了一部分。你能确定它们各是什么三角形吗?
( ) ( ) ( )
学生学习单完成。
学生交流,说出理由。
提问:我们是怎样判断一个三角形是什么三角形的?(看它最大的角)。
追尾:第三幅图,你知道最大角是什么吗?(无法确定)。
小结:这题解决了,用到了什么知识?
3.练习十三第10题。
(1)题目:①一个等腰三角形的顶角是70°,它的一个底角是多少度?
②一个等腰三角形的底角是35°,它的顶角是多少度?
引导:在解决图形与几何题时我们可以先画——示意图。
学生学习单完成。
学生交流。
提问:180°-70°求的是什么?为什么要除以2?
小结:这题解决了,用到了什么知识?
(2)变式:一个等腰三角形中有一个角是70°,它的另外两个角各是多少度?
引导:谁来给大家分析分析?(分类讨论)。
引导学生画图,口答结果。
小结:这题完成了,用到了什么知识?
4.练习十三第13题。
题目:李大伯家有一块等腰三角形的菜园,其中两条边的长分别是10米和20米。要在菜园的边上围篱笆,篱笆长是多少米?
提问:篱笆长就是指什么?现在只知道两条边怎么办?
提示:有困难的画示意图。
(预设:10+20+20=50(米) 10+10+20=40(米))
课件出示示意图,说明10米,10米,20米不能围成三角形。
小结:这题完成了,用到了什么知识?
5.练习十三第14题。
题目:用下面的9根小棒正好摆成一个等边三角形和两个等腰三角形。
引导:怎么摆等边三角形?如果摆成等边三角形,需要怎样的小棒?
追问:先用三根摆等边三角形,还剩6根,怎么摆?
课件出示一种摆法。
提问:这是一种摆法,想一想,你还能找到其他摆法吗?
学生尝试,画示意图。
学生交流,得出一共有两种摆法,
小结:这题完成了,用到了什么知识?
6.练习十三第12题。(变式)
题目:下面是2块三角形玻璃打碎后留下的碎片,你知道它们原来各是什么三角形吗?
学生交流。(①锐角三角形,等腰三角形;②锐角三角形,等边三角形)
追问:怎么判断它是等腰三角形的?等边三角形的?
小结:这题完成了,用到了什么知识?
7.小结:学到这里,冷老师想送给大家一句话,
出示:“题目千万条,”。
引导:什么第一条?
出示:“知识第一条。”
说明:当你把知识都理解透了,有关这些知识的题目,你做起来也就游刃有余了。未来我们在三角形领域还有很多新知识,等着我们去探索,等着我们去“游刃有余”。
8. 聪明屋。
引导:冷老师家有一块三角形玻璃,不小心哐当、打碎了,我只带了一块玻璃去玻璃店,玻璃店员工就帮我配出了这块完整的三角形玻璃!你知道我带的是哪一块吗?
同桌交流,全班交流。
三、全课总结。
1.提问:通过今天的练习课,你有哪些收获
2.课后延学:练习十三第9题(分),练习十三第11题(拼)。
①在直角三角形中画一条线段,把它分成两个三角形。
你分成了两个什么三角形?还可以怎样分?
②用两块完全一样的三角尺拼一拼。(画一画示意图)
(1)拼成图形的内角和是180°。
(2)拼成图形的内角和是360°。
底
底
3cm 5cm 8cm
【教学内容】
苏教版义务教育教科书《数学》四年级下册第86~87页练习十三第7~14题。
【教学目标】
1.使学生进一步认识三角形,巩固三角形边的关系、内角和、三角形分类的有关知识,能应用三角形的知识解决相关问题。
2.使学生在应用知识进行判断、推理和解决问题等活动中,提高分析、判断、推理等思维能力,进一步体会分类、演绎等数学思想方法,感受解决问题方法的多样,发展空间观念。
3.使学生了解三角形的丰富内容,获得应用知识的成功体验,产生对数学知识的兴趣,提高学习数学的自信心和积极性。
【教学重点】
学会三角形知识的应用。
【教学难点】
应用知识分析推理和解释。
【教学准备】
几何画板课件、PPT课件、学习单
【教学过程】
一、知识整理
1.回顾内容。
引导:孩子们,课前我们通过学习单上的理学,对最近学习的三角形的知识进行了简单的复习,本节课我们先来把这些知识一起整理整理。
2.复习三角形基本特征。
(1)复习三个顶点。
提问:你知道怎样的图形是三角形吗?(板书:三条线段首尾相接围成的图形)
三角形有什么特征?(板书:3个顶点、3条边和3个角,稳定性。)
出示:出示几何画板A、B两点。
提问:这是A、B两点,可以连成一条线段,现在要找第三个点C,连成三角形,那么对第三个点有没有什么要求?(板书:不在同一直线上)
出示:出示几何画板。
(2)复习三边关系。
提问:对于三角形的三边关系,你掌握了什么?(板书:任意两边之和大于第三边)
出示:几何画板三角形三边关系数据。
说明:这是一个一般三角形,两边之和大于第三边,不管怎么改变,任意两边之和始终大于第三边。
引导:移动一个顶点,仔细看这组数据,你想说什么?(当两边之和等于第三边,不能围成三角形。)
(3)复习三角形内角和。
提问:三角形的内角和是——180°(板书:内角和180°),还记得课堂上是怎样证明的?(通过剪纸把三个角拼起来)
出示:几何画板三角形。(几何画板平移旋转)
引导:经过平移和旋转,三个角拼起来是什么?(拼成了一个平角)
追问:所以三角形的内角和是?(180°。)
3.复习三角形的分类。
(1)三角形按角分类。
①引导:三角形除了这些基本特征,你还掌握了哪些知识
提问:三角形是怎样分类的,分成哪几类 (板书:锐角三角形,直角三角形,钝角三角形)
出示:出示几何画板线段AB。
引导:我们先来复习特殊的直角三角形,AB两点连成一条线段,请你找一下第三个点C,使ABC三个点连起来是直角三角形。
学生上台找一找。
说明:在两条垂线上,当然A、B两点除外。
引导:刚刚找到了角A是直角,角B是直角,那角C是可以是直角吗?(利用三角尺演示)
说明:现在角C是直角,点C不止这一个,仔细观察角C这个点走过的轨迹。
出示:出示几何画板动画。
说明:点C走过的轨迹是一个圆,真好!原来三角形还和圆有关系。
小结:所以,要想连成直角三角形,点C可以在这两条垂线上,也可以在这个圆上,当然A和B两点除外!
②引导:接着,请你找一下点C,使ABC三个点连起来是锐角三角形。
学生上台找一找。
(出示几何画板,显示各角度数,显示锐角区域)
③引导:最后,请你找一下点C,使ABC三个点连起来是钝角三角形。
学生上台找一找,说明钝角区域。
(2)三角形按边分类。
引导:刚刚我们复习了三角形按角分类。那三角形还可以——按边分类。
说明:特殊的等腰三角形和等边三角形,其他的三条边都不等的叫做一般三角形。
追问:一般三角形指什么?
出示:出示几何画板线段AB。
引导:以线段AB为底,请你找第三个点C,使三角形ABC是一个等腰三角形。
学生上台指一指。
(预设:在对称轴上。说明:等腰三角形是轴对称图形)
出示:几何画板连接三角形,出示三角形各边长,两边相等。
出示:几何画板出示角度,底角相等。
说明:等腰三角形两边相等,底角相等。
引导:(几何画板改变形状)不管我怎么改变三角形的形状,它始终是一个等腰三角形。
提问:我们说等边三角形是特殊的等腰三角形,那么点C移动到哪里时,三角形会是一个等边三角形?
学生上台指一指。
演示:我移动,你们说停我就停。
提问:为什么现在叫我停了?
(三条边都相等时,也就是当等腰三角形的腰和底相等时,就是一个等边三角形。)
追问:仔细看看,你还有什么发现?(三个角都是60°。)
追问:只有这一个点C吗?(下面还有一个)
(3)集合圈
引导:孩子们,你们掌握的真好,按角分类,如果用一个圈来表示所有的三角形的家,那锐角、直角、钝角三角形应该住在哪?
学生黑板移一移。
引导:按边分类,如果用一个圈来表示所有的三角形的家,它们住在哪?
学生黑板移一移。
二、巩固练习
引入:知识需要巩固和应用,下面我们一起来练习三角形的内容,看看每题都用到了什么知识。(板书:用到了什么知识?)
1.练习十三第7题(变式)。
(1)题目:判断下面各是什么三角形。
学生判断,说出理由。
提问:仔细观察第二个直角三角形,你还发现什么?
说明:两条边相等,它也是一个等腰三角形,合起来它就是等腰直角三角形。
(2)题目:画出下面三角形底边上的高。
交流:什么是三角形的高?画高要注意什么?
学生投影展示(钝角三角形画高),有错纠正,同桌检查。
提问:观察三条高的位置,你有什么发现?(三角形的高可能在三角形的里面,可能在三角形的边上,可能在三角形的外面。)
小结:这题解决了,用到了什么知识?
2.练习十三第8题。
题目:下面的三角形都被一张纸遮住了一部分。你能确定它们各是什么三角形吗?
( ) ( ) ( )
学生学习单完成。
学生交流,说出理由。
提问:我们是怎样判断一个三角形是什么三角形的?(看它最大的角)。
追尾:第三幅图,你知道最大角是什么吗?(无法确定)。
小结:这题解决了,用到了什么知识?
3.练习十三第10题。
(1)题目:①一个等腰三角形的顶角是70°,它的一个底角是多少度?
②一个等腰三角形的底角是35°,它的顶角是多少度?
引导:在解决图形与几何题时我们可以先画——示意图。
学生学习单完成。
学生交流。
提问:180°-70°求的是什么?为什么要除以2?
小结:这题解决了,用到了什么知识?
(2)变式:一个等腰三角形中有一个角是70°,它的另外两个角各是多少度?
引导:谁来给大家分析分析?(分类讨论)。
引导学生画图,口答结果。
小结:这题完成了,用到了什么知识?
4.练习十三第13题。
题目:李大伯家有一块等腰三角形的菜园,其中两条边的长分别是10米和20米。要在菜园的边上围篱笆,篱笆长是多少米?
提问:篱笆长就是指什么?现在只知道两条边怎么办?
提示:有困难的画示意图。
(预设:10+20+20=50(米) 10+10+20=40(米))
课件出示示意图,说明10米,10米,20米不能围成三角形。
小结:这题完成了,用到了什么知识?
5.练习十三第14题。
题目:用下面的9根小棒正好摆成一个等边三角形和两个等腰三角形。
引导:怎么摆等边三角形?如果摆成等边三角形,需要怎样的小棒?
追问:先用三根摆等边三角形,还剩6根,怎么摆?
课件出示一种摆法。
提问:这是一种摆法,想一想,你还能找到其他摆法吗?
学生尝试,画示意图。
学生交流,得出一共有两种摆法,
小结:这题完成了,用到了什么知识?
6.练习十三第12题。(变式)
题目:下面是2块三角形玻璃打碎后留下的碎片,你知道它们原来各是什么三角形吗?
学生交流。(①锐角三角形,等腰三角形;②锐角三角形,等边三角形)
追问:怎么判断它是等腰三角形的?等边三角形的?
小结:这题完成了,用到了什么知识?
7.小结:学到这里,冷老师想送给大家一句话,
出示:“题目千万条,”。
引导:什么第一条?
出示:“知识第一条。”
说明:当你把知识都理解透了,有关这些知识的题目,你做起来也就游刃有余了。未来我们在三角形领域还有很多新知识,等着我们去探索,等着我们去“游刃有余”。
8. 聪明屋。
引导:冷老师家有一块三角形玻璃,不小心哐当、打碎了,我只带了一块玻璃去玻璃店,玻璃店员工就帮我配出了这块完整的三角形玻璃!你知道我带的是哪一块吗?
同桌交流,全班交流。
三、全课总结。
1.提问:通过今天的练习课,你有哪些收获
2.课后延学:练习十三第9题(分),练习十三第11题(拼)。
①在直角三角形中画一条线段,把它分成两个三角形。
你分成了两个什么三角形?还可以怎样分?
②用两块完全一样的三角尺拼一拼。(画一画示意图)
(1)拼成图形的内角和是180°。
(2)拼成图形的内角和是360°。
底
底
3cm 5cm 8cm
