苏科版数学七年级下册同步课时训练:第9章 整式乘法与因式分解 单元复习小结(word版 含解析)
文档属性
| 名称 | 苏科版数学七年级下册同步课时训练:第9章 整式乘法与因式分解 单元复习小结(word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 76.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-04 10:32:19 | ||
图片预览


文档简介
小结
类型之一 整式的乘法
1.(2020东营)下列运算正确的是 ( )
A.(x3)2=x5
B.(x-y)2=x2+y2
C.-x2y3·2xy2=-2x3y5
D.-(3x+y)=-3x+y
2.(2021苏州姑苏区期中)若(x+2)(2x-n)=2x2+mx+2,则m-n的值是 ( )
A.6 B.4 C.2 D.-6
3.(2021扬州广陵区期中)已知式子(ax-1)(x+4)-x2-b化简后,不含有x2项和常数项.
(1)求a,b的值;
(2)求(-a-b)2-a(2a+b)的值.
类型之二 乘法公式的运用
4.将图9-X-1①中阴影小长方形变换到图②位置,根据两个图形的面积关系可以得到一个关于a,b的恒等式为 ( )
图9-X-1
A.(a-b)2=a2-2ab+b2
B.(a+b)2=a2+2ab+b2
C.(a+b)(a-b)=a2-b2
D.a(a-b)=a2-ab
5.(2021靖江模拟)若a2+4a=5,则代数式2a(a+2)-(a+1)(a-1)的值为 ( )
A.1 B.2 C.4 D.6
6.(2020宿迁)已知a+b=3,a2+b2=5,则ab= .
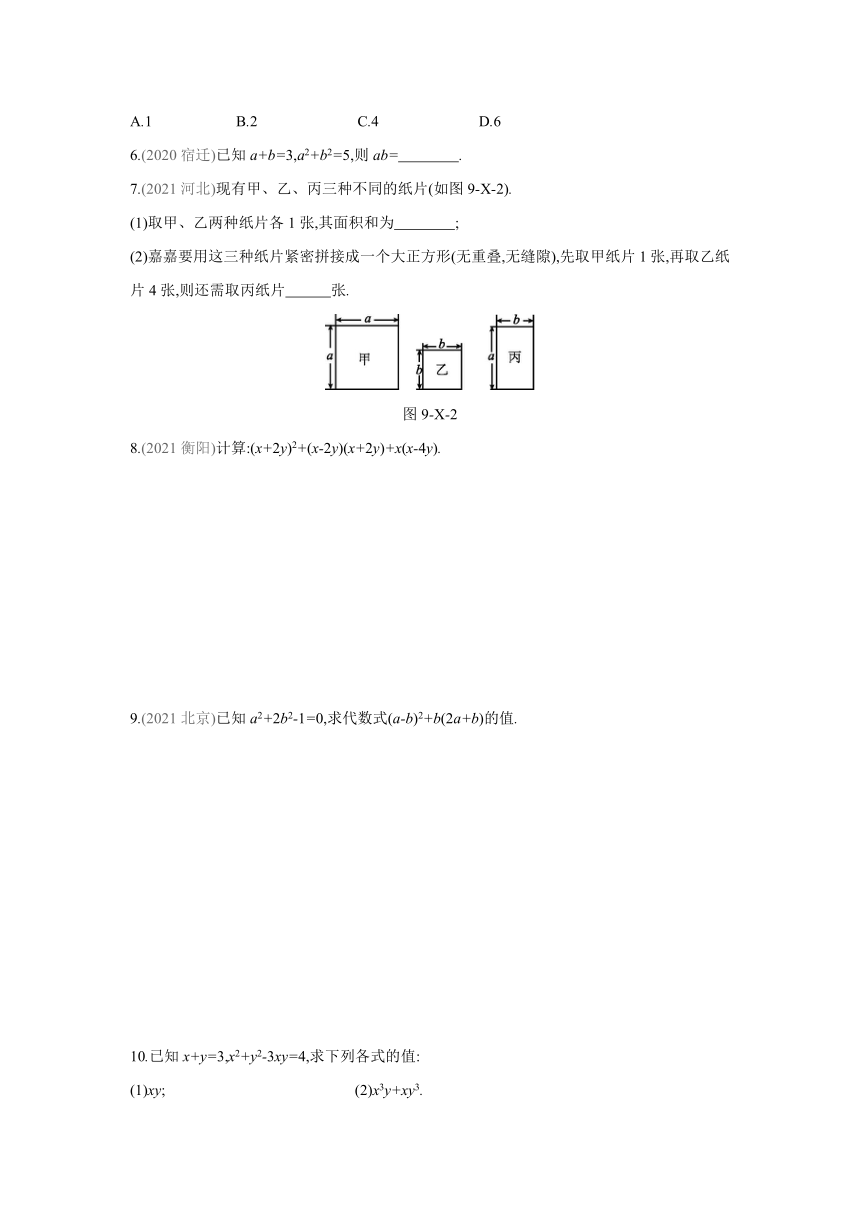
7.(2021河北)现有甲、乙、丙三种不同的纸片(如图9-X-2).
(1)取甲、乙两种纸片各1张,其面积和为 ;
(2)嘉嘉要用这三种纸片紧密拼接成一个大正方形(无重叠,无缝隙),先取甲纸片1张,再取乙纸片4张,则还需取丙纸片 张.
图9-X-2
8.(2021衡阳)计算:(x+2y)2+(x-2y)(x+2y)+x(x-4y).
9.(2021北京)已知a2+2b2-1=0,求代数式(a-b)2+b(2a+b)的值.
10.已知x+y=3,x2+y2-3xy=4,求下列各式的值:
(1)xy; (2)x3y+xy3.
类型之三 因式分解
11.(2021贺州)多项式2x3-4x2+2x因式分解的结果为 ( )
A.2x(x-1)2 B.2x(x+1)2
C.x(2x-1)2 D.x(2x+1)2
12.因式分解:
(1)(2021常州)x2-4y2= ;
(2)(2021无锡)2x3-8x= ;
(3)(2021菏泽)-a3+2a2-a= ;
(4)(2021湖北)5x4-5x2= .
13.(2021扬州)计算:20212-20202= .
14.(2021苏州)若m+2n=1,则3m2+6mn+6n的值为 .
15.(2021十堰)已知xy=2,x-3y=3,则2x3y-12x2y2+18xy3= .
16.(2021苏州姑苏区期中)已知a+b=,ab=,并满足a>b,则a2-b2= .
类型之四 数学活动
17.如图9-X-3,用四个完全一样的长、宽分别为x,y的长方形纸片围成一个大正方形ABCD,中间是空的小正方形EFGH.若AB=a,EF=b,有以下关系式:①x+y=a;②x-y=b;③a2-b2=2xy;④x2-y2=ab;⑤x2+y2=.其中正确的是 .(填序号)
图9-X-3
18.如果一个正整数能表示成两个连续偶数的平方差,那么称这个正整数为“巧数”,如:4=22-02,12=42-22,20=62-42,因此4,12,20这三个数都是“巧数”.
(1)400和2020这两个数是巧数吗 为什么
(2)设两个连续偶数为2n和2n-2(其中n取正整数),由这两个连续偶数构造的“巧数”是4的整数倍吗 为什么
(3)求介于50到101之间所有“巧数”的和.
答案
小结与思考
1.C (x3)2=x6;(x-y)2=x2-2xy+y2;-(3x+y)=-3x-y,故选项A,B,D错误.
2.A (x+2)(2x-n)=2x2+(4-n)x-2n=2x2+mx+2,
则4-n=m,-2n=2,
解得m=5,n=-1,
所以m-n=5-(-1)=6.
3.解:(1)原式=ax2+4ax-x-4-x2-b=(a-1)x2+(4a-1)x-4-b.
因为原式化简后,不含有x2项和常数项,
所以a-1=0,-4-b=0,
解得a=1,b=-4.
(2)原式=a2+2ab+b2-2a2-ab=-a2+ab+b2.
当a=1,b=-4时,原式=-1-4+16=11.
4.C 图①的面积为(a-b)(a+b),图②的面积为a(a-b+b)-b·b=a2-b2.
因为两图形的面积相等,
所以关于a,b的恒等式为(a+b)(a-b)=a2-b2.故选C.
5.D 当a2+4a=5时,原式=2a2+4a-a2+1=(a2+4a)+1=6.
6.2 因为a2+b2=(a+b)2-2ab,
a+b=3,a2+b2=5,
所以5=32-2ab,即2ab=4,所以ab=2.
7.(1)a2+b2 (2)4
8.解:原式=(x2+4xy+4y2)+(x2-4y2)+(x2-4xy)=x2+4xy+4y2+x2-4y2+x2-4xy=3x2.
9.解:原式=a2-2ab+b2+2ab+b2=a2+2b2.
由a2+2b2-1=0,得a2+2b2=1,
则原式=1.
10. (1)本题可将条件x+y=3的两边平方后与x2+y2-3xy=4相减求得xy的值;
(2)将所给代数式提公因式后转化为含“x+y”与“xy”的形式,再整体代入.
解:(1)因为x+y=3,所以=9,即x2+2xy+y2=9.又因为x2+y2-3xy=4,两等式左右两边分别相减得5xy=5,所以xy=1.
(2)x3y+xy3=xy(x2+y2)=xy[(x+y)2-2xy]=1×(32-2)=7.
11.A 原式=2x(x2-2x+1)=2x(x-1)2.
12.(1)(x+2y)(x-2y) (2)2x(x+2)(x-2)
(3)-a(a-1)2 (4)5x2(x+1)(x-1)
13.4041 20212-20202
=(2021+2020)(2021-2020)
=4041×1
=4041.
14.3 由m+2n=1,得3m2+6mn+6n=3m(m+2n)+6n=3m×1+6n=3m+6n=3(m+2n)=3.
15.36 原式=2xy(x2-6xy+9y2)=2xy(x-3y)2.当xy=2,x-3y=3时,原式=2×2×32=36.
16. 由a+b=,得(a+b)2=,
则a2+2ab+b2=,所以a2+b2=,
于是(a-b)2=a2-2ab+b2=.
因为a>b,所以a-b=,
所以a2-b2=(a+b)(a-b)=.
17.①②④⑤ 由图形可得①大正方形ABCD的边长=长方形的长+长方形的宽,故x+y=a,正确;②小正方形EFGH的边长=长方形的长-长方形的宽,故x-y=b,正确;③大正方形ABCD的面积-小正方形EFGH的面积=4个长方形的面积,故a2-b2=4xy,错误;④根据①知x+y=a,根据②知x-y=b,则x2-y2=ab,正确;⑤x2+y2=(x+y)2-2xy=a2-2×=,正确.所以正确的是①②④⑤.
18.解:(1)400不是“巧数”,2020是“巧数”.理由如下:
因为400不能写成两个连续偶数的平方差,故400不是“巧数”;
因为2020=5062-5042,故2020是“巧数”.
(2)是.理由如下:(2n)2-(2n-2)2
=(2n+2n-2)(2n-2n+2)
=2(4n-2)
=4(2n-1).
因为n为正整数,
所以2n-1一定为正整数,
所以4(2n-1)一定能被4整除,
所以由这两个连续偶数构造的“巧数”是4的整数倍.
(3)介于50到101之间所有“巧数”的和为
(142-122)+(162-142)+(182-162)+…+(262-242)
=262-122
=532.
类型之一 整式的乘法
1.(2020东营)下列运算正确的是 ( )
A.(x3)2=x5
B.(x-y)2=x2+y2
C.-x2y3·2xy2=-2x3y5
D.-(3x+y)=-3x+y
2.(2021苏州姑苏区期中)若(x+2)(2x-n)=2x2+mx+2,则m-n的值是 ( )
A.6 B.4 C.2 D.-6
3.(2021扬州广陵区期中)已知式子(ax-1)(x+4)-x2-b化简后,不含有x2项和常数项.
(1)求a,b的值;
(2)求(-a-b)2-a(2a+b)的值.
类型之二 乘法公式的运用
4.将图9-X-1①中阴影小长方形变换到图②位置,根据两个图形的面积关系可以得到一个关于a,b的恒等式为 ( )
图9-X-1
A.(a-b)2=a2-2ab+b2
B.(a+b)2=a2+2ab+b2
C.(a+b)(a-b)=a2-b2
D.a(a-b)=a2-ab
5.(2021靖江模拟)若a2+4a=5,则代数式2a(a+2)-(a+1)(a-1)的值为 ( )
A.1 B.2 C.4 D.6
6.(2020宿迁)已知a+b=3,a2+b2=5,则ab= .
7.(2021河北)现有甲、乙、丙三种不同的纸片(如图9-X-2).
(1)取甲、乙两种纸片各1张,其面积和为 ;
(2)嘉嘉要用这三种纸片紧密拼接成一个大正方形(无重叠,无缝隙),先取甲纸片1张,再取乙纸片4张,则还需取丙纸片 张.
图9-X-2
8.(2021衡阳)计算:(x+2y)2+(x-2y)(x+2y)+x(x-4y).
9.(2021北京)已知a2+2b2-1=0,求代数式(a-b)2+b(2a+b)的值.
10.已知x+y=3,x2+y2-3xy=4,求下列各式的值:
(1)xy; (2)x3y+xy3.
类型之三 因式分解
11.(2021贺州)多项式2x3-4x2+2x因式分解的结果为 ( )
A.2x(x-1)2 B.2x(x+1)2
C.x(2x-1)2 D.x(2x+1)2
12.因式分解:
(1)(2021常州)x2-4y2= ;
(2)(2021无锡)2x3-8x= ;
(3)(2021菏泽)-a3+2a2-a= ;
(4)(2021湖北)5x4-5x2= .
13.(2021扬州)计算:20212-20202= .
14.(2021苏州)若m+2n=1,则3m2+6mn+6n的值为 .
15.(2021十堰)已知xy=2,x-3y=3,则2x3y-12x2y2+18xy3= .
16.(2021苏州姑苏区期中)已知a+b=,ab=,并满足a>b,则a2-b2= .
类型之四 数学活动
17.如图9-X-3,用四个完全一样的长、宽分别为x,y的长方形纸片围成一个大正方形ABCD,中间是空的小正方形EFGH.若AB=a,EF=b,有以下关系式:①x+y=a;②x-y=b;③a2-b2=2xy;④x2-y2=ab;⑤x2+y2=.其中正确的是 .(填序号)
图9-X-3
18.如果一个正整数能表示成两个连续偶数的平方差,那么称这个正整数为“巧数”,如:4=22-02,12=42-22,20=62-42,因此4,12,20这三个数都是“巧数”.
(1)400和2020这两个数是巧数吗 为什么
(2)设两个连续偶数为2n和2n-2(其中n取正整数),由这两个连续偶数构造的“巧数”是4的整数倍吗 为什么
(3)求介于50到101之间所有“巧数”的和.
答案
小结与思考
1.C (x3)2=x6;(x-y)2=x2-2xy+y2;-(3x+y)=-3x-y,故选项A,B,D错误.
2.A (x+2)(2x-n)=2x2+(4-n)x-2n=2x2+mx+2,
则4-n=m,-2n=2,
解得m=5,n=-1,
所以m-n=5-(-1)=6.
3.解:(1)原式=ax2+4ax-x-4-x2-b=(a-1)x2+(4a-1)x-4-b.
因为原式化简后,不含有x2项和常数项,
所以a-1=0,-4-b=0,
解得a=1,b=-4.
(2)原式=a2+2ab+b2-2a2-ab=-a2+ab+b2.
当a=1,b=-4时,原式=-1-4+16=11.
4.C 图①的面积为(a-b)(a+b),图②的面积为a(a-b+b)-b·b=a2-b2.
因为两图形的面积相等,
所以关于a,b的恒等式为(a+b)(a-b)=a2-b2.故选C.
5.D 当a2+4a=5时,原式=2a2+4a-a2+1=(a2+4a)+1=6.
6.2 因为a2+b2=(a+b)2-2ab,
a+b=3,a2+b2=5,
所以5=32-2ab,即2ab=4,所以ab=2.
7.(1)a2+b2 (2)4
8.解:原式=(x2+4xy+4y2)+(x2-4y2)+(x2-4xy)=x2+4xy+4y2+x2-4y2+x2-4xy=3x2.
9.解:原式=a2-2ab+b2+2ab+b2=a2+2b2.
由a2+2b2-1=0,得a2+2b2=1,
则原式=1.
10. (1)本题可将条件x+y=3的两边平方后与x2+y2-3xy=4相减求得xy的值;
(2)将所给代数式提公因式后转化为含“x+y”与“xy”的形式,再整体代入.
解:(1)因为x+y=3,所以=9,即x2+2xy+y2=9.又因为x2+y2-3xy=4,两等式左右两边分别相减得5xy=5,所以xy=1.
(2)x3y+xy3=xy(x2+y2)=xy[(x+y)2-2xy]=1×(32-2)=7.
11.A 原式=2x(x2-2x+1)=2x(x-1)2.
12.(1)(x+2y)(x-2y) (2)2x(x+2)(x-2)
(3)-a(a-1)2 (4)5x2(x+1)(x-1)
13.4041 20212-20202
=(2021+2020)(2021-2020)
=4041×1
=4041.
14.3 由m+2n=1,得3m2+6mn+6n=3m(m+2n)+6n=3m×1+6n=3m+6n=3(m+2n)=3.
15.36 原式=2xy(x2-6xy+9y2)=2xy(x-3y)2.当xy=2,x-3y=3时,原式=2×2×32=36.
16. 由a+b=,得(a+b)2=,
则a2+2ab+b2=,所以a2+b2=,
于是(a-b)2=a2-2ab+b2=.
因为a>b,所以a-b=,
所以a2-b2=(a+b)(a-b)=.
17.①②④⑤ 由图形可得①大正方形ABCD的边长=长方形的长+长方形的宽,故x+y=a,正确;②小正方形EFGH的边长=长方形的长-长方形的宽,故x-y=b,正确;③大正方形ABCD的面积-小正方形EFGH的面积=4个长方形的面积,故a2-b2=4xy,错误;④根据①知x+y=a,根据②知x-y=b,则x2-y2=ab,正确;⑤x2+y2=(x+y)2-2xy=a2-2×=,正确.所以正确的是①②④⑤.
18.解:(1)400不是“巧数”,2020是“巧数”.理由如下:
因为400不能写成两个连续偶数的平方差,故400不是“巧数”;
因为2020=5062-5042,故2020是“巧数”.
(2)是.理由如下:(2n)2-(2n-2)2
=(2n+2n-2)(2n-2n+2)
=2(4n-2)
=4(2n-1).
因为n为正整数,
所以2n-1一定为正整数,
所以4(2n-1)一定能被4整除,
所以由这两个连续偶数构造的“巧数”是4的整数倍.
(3)介于50到101之间所有“巧数”的和为
(142-122)+(162-142)+(182-162)+…+(262-242)
=262-122
=532.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
