苏科版数学七年级下册同步课时训练:第7章 平面图形的认识(二) 单元复习小结与思考(word版 含解析)
文档属性
| 名称 | 苏科版数学七年级下册同步课时训练:第7章 平面图形的认识(二) 单元复习小结与思考(word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 154.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-04 10:41:36 | ||
图片预览


文档简介
小结与思考
类型之一 平行线的判定和性质
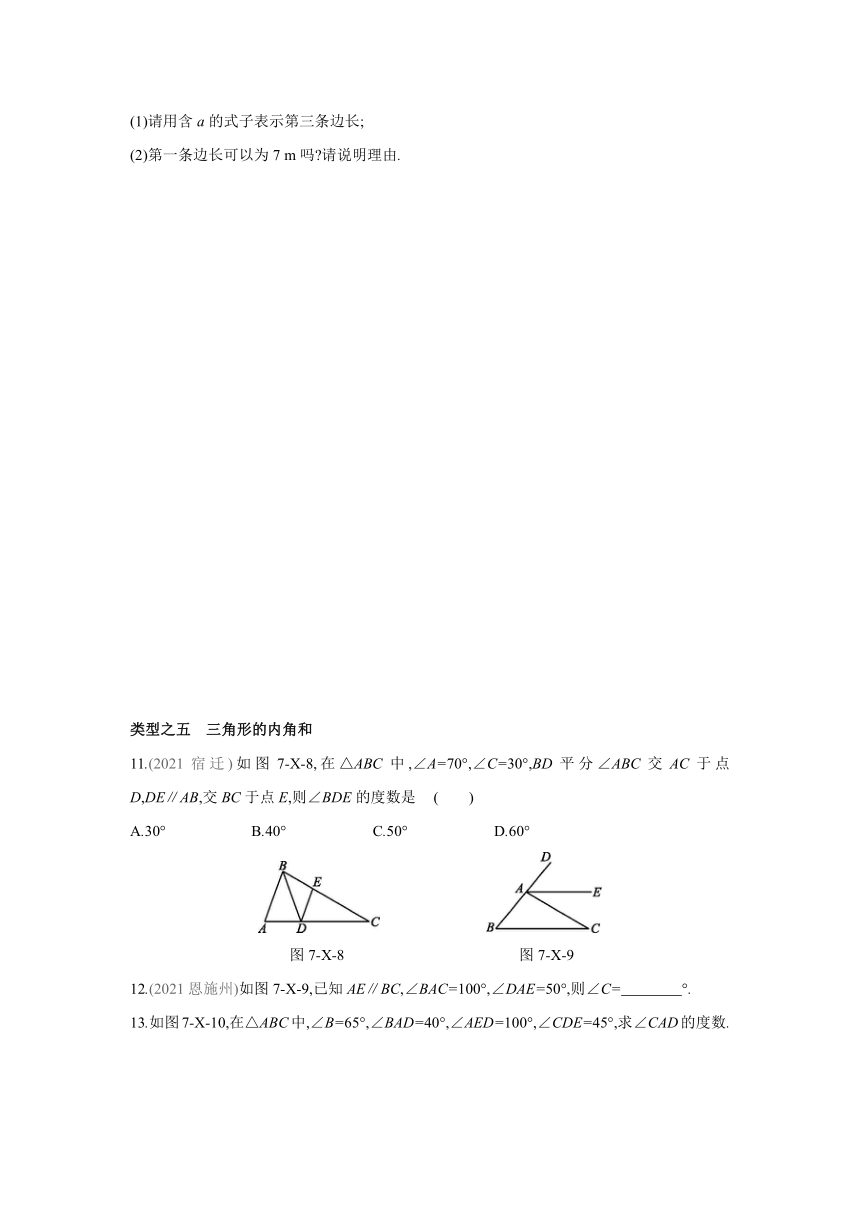
1.(2021新疆)如图7-X-1,直线DE过点A,且DE∥BC.若∠B=60°,∠1=50°,则∠2的度数为( )
A.50° B.60° C.70° D.80°
图7-X-1 图7-X-2
2.(2021泰州)如图7-X-2,木棒AB,CD与EF分别在G,H处用可旋转的螺丝铆住,∠EGB=100°,∠EHD=80°,将木棒AB绕点G逆时针旋转到与木棒CD平行的位置,则至少要旋转 °.
类型之二 平行线与三角形的综合运用
3.(2021随州)如图7-X-3,将一块含有60°角的三角尺放置在两条平行线上,若∠1=45°,则∠2为 ( )
A.15° B.25° C.35° D.45°
图7-X-3 图7-X-4
4.(2021常州)如图7-X-4,在△ABC中,点D,E分别在BC,AC上,∠B=40°,∠C=60°,若DE∥AB,则∠AED= °.
类型之三 平移
5.如图7-X-5,四边形EFGH是由四边形ABCD平移得到的,已知AD=5,∠B=70°,则 ( )
图7-X-5
A.FG=5,∠G=70° B.EH=5,∠F=70°
C.EF=5,∠F=70° D.EF=5,∠E=70°
6.如图7-X-6,△ABC沿着BC方向平移到△DEF,已知BC=6,EC=2,那么平移的距离为( )
图7-X-6
A.2 B.4 C.6 D.8
7.(2021盐城盐都区期末)如图7-X-7是由边长均为1的小正方形构成的网格,点A,B,C都在格点上,将△ABC向右平移3个单位长度,再向上平移2个单位长度得到△A1B1C1.
(1)在网格中画出△A1B1C1;
(2)求线段AB在变换到A1B1过程中扫过的区域面积(重叠部分不重复计算).
图7-X-7
类型之四 三角形的三边关系
8.(2021南京)下列长度的三条线段与长度为5的线段能组成四边形的是 ( )
A.1,1,1 B.1,1,8
C.1,2,2 D.2,2,2
9.已知a,b,c是△ABC的三边长,a,b满足|a-7|+(b-1)2=0,c为奇数,则c= .
10.小王准备用一段长30 m的篱笆围成一个三角形形状的场地,用于饲养家兔,已知第一条边长为a m,由于受地势限制,第二条边长只能是第一条边长的2倍多2 m.
(1)请用含a的式子表示第三条边长;
(2)第一条边长可以为7 m吗 请说明理由.
类型之五 三角形的内角和
11.(2021宿迁)如图7-X-8,在△ABC中,∠A=70°,∠C=30°,BD平分∠ABC交AC于点D,DE∥AB,交BC于点E,则∠BDE的度数是 ( )
A.30° B.40° C.50° D.60°
图7-X-8 图7-X-9
12.(2021恩施州)如图7-X-9,已知AE∥BC,∠BAC=100°,∠DAE=50°,则∠C= °.
13.如图7-X-10,在△ABC中,∠B=65°,∠BAD=40°,∠AED=100°,∠CDE=45°,求∠CAD的度数.
图7-X-10
类型之六 多边形的内角和与外角和
14.(2021云南)一个十边形的内角和等于 ( )
A.1800° B.1660° C.1440° D.1200°
15.(2021绥化)一个多边形的内角和是外角和的4倍,则这个多边形是 ( )
A.八边形 B.九边形 C.十边形 D.十二边形
16.(2021扬州)如图7-X-11,点A,B,C,D,E在同一平面内,连接AB,BC,CD,DE,EA,若∠BCD=100°,则∠A+∠B+∠D+∠E为( )
图7-X-11
A.220° B.240° C.260° D.280°
17.(2021盐城)若一个多边形的每个外角均为40°,则这个多边形的边数为 .
18.(2021丽水)一个多边形过顶点剪去一个角后,所得多边形的内角和为720°,则原多边形的边数是 .
答案
小结与思考
1.C 由DE∥BC,得∠DAB=∠B=60°,则∠2=180°-∠DAB-∠1=180°-60°-50°=70°.
2.20 当∠EGB=∠EHD=80°时,AB∥CD,木棒AB绕点G逆时针至少要旋转的角度为100°-80°=20°.
3.A 如图,过三角尺的60°角的顶点F作EF∥AB,则∠EFG=∠1=45°,而∠EFG+∠EFH=60°,得∠EFH=60°-∠EFG=60°-45°=15°.因为AB∥CD,所以EF∥CD,所以∠2=∠EFH=15°.
4.100 在△ABC中,∠A+∠B+∠C=180°,而∠B=40°,∠C=60°,
则∠A=180°-∠B-∠C=180°-40°-60°=80°.
由DE∥AB,可得∠A+∠AED=180°,所以∠AED=180°-80°=100°.
5.B 由四边形EFGH是由四边形ABCD平移得到的,可知EH是AD的对应边,∠F是∠B的对应角.因为AD=5,∠B=70°,所以EH=5,∠F=70°.故选B.
6.B 由题意知BE=BC-EC=6-2=4,故平移的距离为4.故选B.
7.(1)略 (2)7 8.D
9.7 因为a,b满足|a-7|+(b-1)2=0,所以a-7=0,b-1=0,解得a=7,b=1.因为7-1=6,7+1=8,所以610.解:(1)第三条边长为30-a-(2a+2)=(28-3a)m.
(2)第一条边长不可以为7 m.理由:当a=7时,三边长分别为7 m,16 m,7 m.因为7+7<16,
所以7 m,7 m,16 m不能构成三角形,即第一条边长不可以为7 m.
11.B 在△ABC中,∠A=70°,∠C=30°,可得∠ABC=180°-∠A-∠C=80°,
而BD平分∠ABC,则∠ABD=∠ABC=40°.又DE∥AB,所以∠BDE=∠ABD=40°.
12.30 由AE∥BC,得∠B=∠DAE=50°.在△ABC中,∠C=180°-∠BAC-∠B=30°.
13.解:在△ABD中,因为∠B=65°,∠BAD=40°,
所以∠BDA=180°-(∠B+∠BAD)=180°-(65°+40°)=75°.
因为∠CDE=45°,所以∠ADE=180°-(∠BDA+∠CDE)=180°-(75°+45°)=60°.
在△ADE中,因为∠AED=100°,所以∠CAD=180°-∠ADE-∠AED=180°-60°-100°=20°.
14.C 根据多边形内角和公式,得十边形的内角和为(10-2)×180°=8×180°=1440°.
15.C 设这个多边形的边数为n,则该多边形的内角和为(n-2)×180°.
依题意得(n-2)×180°=360°×4,解得n=10,所以这个多边形是十边形.
16.D 如图,连接BD,由∠BCD=100°,得∠CBD+∠CDB=180°-100°=80°,
则∠A+∠ABC+∠E+∠CDE=360°-∠CBD-∠CDB=360°-80°=280°.
17.9 一个多边形的外角和为360°,而每个外角为40°,进而求出外角的个数,即为多边形的边数.
18.6或7 设内角和为720°的多边形的边数是n,则(n-2)·180=720,解得n=6.而多边形过顶点截去一个角后边数不变或减少1,则原多边形的边数为6或7.
类型之一 平行线的判定和性质
1.(2021新疆)如图7-X-1,直线DE过点A,且DE∥BC.若∠B=60°,∠1=50°,则∠2的度数为( )
A.50° B.60° C.70° D.80°
图7-X-1 图7-X-2
2.(2021泰州)如图7-X-2,木棒AB,CD与EF分别在G,H处用可旋转的螺丝铆住,∠EGB=100°,∠EHD=80°,将木棒AB绕点G逆时针旋转到与木棒CD平行的位置,则至少要旋转 °.
类型之二 平行线与三角形的综合运用
3.(2021随州)如图7-X-3,将一块含有60°角的三角尺放置在两条平行线上,若∠1=45°,则∠2为 ( )
A.15° B.25° C.35° D.45°
图7-X-3 图7-X-4
4.(2021常州)如图7-X-4,在△ABC中,点D,E分别在BC,AC上,∠B=40°,∠C=60°,若DE∥AB,则∠AED= °.
类型之三 平移
5.如图7-X-5,四边形EFGH是由四边形ABCD平移得到的,已知AD=5,∠B=70°,则 ( )
图7-X-5
A.FG=5,∠G=70° B.EH=5,∠F=70°
C.EF=5,∠F=70° D.EF=5,∠E=70°
6.如图7-X-6,△ABC沿着BC方向平移到△DEF,已知BC=6,EC=2,那么平移的距离为( )
图7-X-6
A.2 B.4 C.6 D.8
7.(2021盐城盐都区期末)如图7-X-7是由边长均为1的小正方形构成的网格,点A,B,C都在格点上,将△ABC向右平移3个单位长度,再向上平移2个单位长度得到△A1B1C1.
(1)在网格中画出△A1B1C1;
(2)求线段AB在变换到A1B1过程中扫过的区域面积(重叠部分不重复计算).
图7-X-7
类型之四 三角形的三边关系
8.(2021南京)下列长度的三条线段与长度为5的线段能组成四边形的是 ( )
A.1,1,1 B.1,1,8
C.1,2,2 D.2,2,2
9.已知a,b,c是△ABC的三边长,a,b满足|a-7|+(b-1)2=0,c为奇数,则c= .
10.小王准备用一段长30 m的篱笆围成一个三角形形状的场地,用于饲养家兔,已知第一条边长为a m,由于受地势限制,第二条边长只能是第一条边长的2倍多2 m.
(1)请用含a的式子表示第三条边长;
(2)第一条边长可以为7 m吗 请说明理由.
类型之五 三角形的内角和
11.(2021宿迁)如图7-X-8,在△ABC中,∠A=70°,∠C=30°,BD平分∠ABC交AC于点D,DE∥AB,交BC于点E,则∠BDE的度数是 ( )
A.30° B.40° C.50° D.60°
图7-X-8 图7-X-9
12.(2021恩施州)如图7-X-9,已知AE∥BC,∠BAC=100°,∠DAE=50°,则∠C= °.
13.如图7-X-10,在△ABC中,∠B=65°,∠BAD=40°,∠AED=100°,∠CDE=45°,求∠CAD的度数.
图7-X-10
类型之六 多边形的内角和与外角和
14.(2021云南)一个十边形的内角和等于 ( )
A.1800° B.1660° C.1440° D.1200°
15.(2021绥化)一个多边形的内角和是外角和的4倍,则这个多边形是 ( )
A.八边形 B.九边形 C.十边形 D.十二边形
16.(2021扬州)如图7-X-11,点A,B,C,D,E在同一平面内,连接AB,BC,CD,DE,EA,若∠BCD=100°,则∠A+∠B+∠D+∠E为( )
图7-X-11
A.220° B.240° C.260° D.280°
17.(2021盐城)若一个多边形的每个外角均为40°,则这个多边形的边数为 .
18.(2021丽水)一个多边形过顶点剪去一个角后,所得多边形的内角和为720°,则原多边形的边数是 .
答案
小结与思考
1.C 由DE∥BC,得∠DAB=∠B=60°,则∠2=180°-∠DAB-∠1=180°-60°-50°=70°.
2.20 当∠EGB=∠EHD=80°时,AB∥CD,木棒AB绕点G逆时针至少要旋转的角度为100°-80°=20°.
3.A 如图,过三角尺的60°角的顶点F作EF∥AB,则∠EFG=∠1=45°,而∠EFG+∠EFH=60°,得∠EFH=60°-∠EFG=60°-45°=15°.因为AB∥CD,所以EF∥CD,所以∠2=∠EFH=15°.
4.100 在△ABC中,∠A+∠B+∠C=180°,而∠B=40°,∠C=60°,
则∠A=180°-∠B-∠C=180°-40°-60°=80°.
由DE∥AB,可得∠A+∠AED=180°,所以∠AED=180°-80°=100°.
5.B 由四边形EFGH是由四边形ABCD平移得到的,可知EH是AD的对应边,∠F是∠B的对应角.因为AD=5,∠B=70°,所以EH=5,∠F=70°.故选B.
6.B 由题意知BE=BC-EC=6-2=4,故平移的距离为4.故选B.
7.(1)略 (2)7 8.D
9.7 因为a,b满足|a-7|+(b-1)2=0,所以a-7=0,b-1=0,解得a=7,b=1.因为7-1=6,7+1=8,所以6
(2)第一条边长不可以为7 m.理由:当a=7时,三边长分别为7 m,16 m,7 m.因为7+7<16,
所以7 m,7 m,16 m不能构成三角形,即第一条边长不可以为7 m.
11.B 在△ABC中,∠A=70°,∠C=30°,可得∠ABC=180°-∠A-∠C=80°,
而BD平分∠ABC,则∠ABD=∠ABC=40°.又DE∥AB,所以∠BDE=∠ABD=40°.
12.30 由AE∥BC,得∠B=∠DAE=50°.在△ABC中,∠C=180°-∠BAC-∠B=30°.
13.解:在△ABD中,因为∠B=65°,∠BAD=40°,
所以∠BDA=180°-(∠B+∠BAD)=180°-(65°+40°)=75°.
因为∠CDE=45°,所以∠ADE=180°-(∠BDA+∠CDE)=180°-(75°+45°)=60°.
在△ADE中,因为∠AED=100°,所以∠CAD=180°-∠ADE-∠AED=180°-60°-100°=20°.
14.C 根据多边形内角和公式,得十边形的内角和为(10-2)×180°=8×180°=1440°.
15.C 设这个多边形的边数为n,则该多边形的内角和为(n-2)×180°.
依题意得(n-2)×180°=360°×4,解得n=10,所以这个多边形是十边形.
16.D 如图,连接BD,由∠BCD=100°,得∠CBD+∠CDB=180°-100°=80°,
则∠A+∠ABC+∠E+∠CDE=360°-∠CBD-∠CDB=360°-80°=280°.
17.9 一个多边形的外角和为360°,而每个外角为40°,进而求出外角的个数,即为多边形的边数.
18.6或7 设内角和为720°的多边形的边数是n,则(n-2)·180=720,解得n=6.而多边形过顶点截去一个角后边数不变或减少1,则原多边形的边数为6或7.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
