苏科版数学七年级下册同步课时训练:7.1 第1课时 利用同位角探索两直线平行的条件(word版 含解析)
文档属性
| 名称 | 苏科版数学七年级下册同步课时训练:7.1 第1课时 利用同位角探索两直线平行的条件(word版 含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 157.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-04 10:45:59 | ||
图片预览

文档简介
7.1 第1课时 利用同位角探索两直线平行的条件
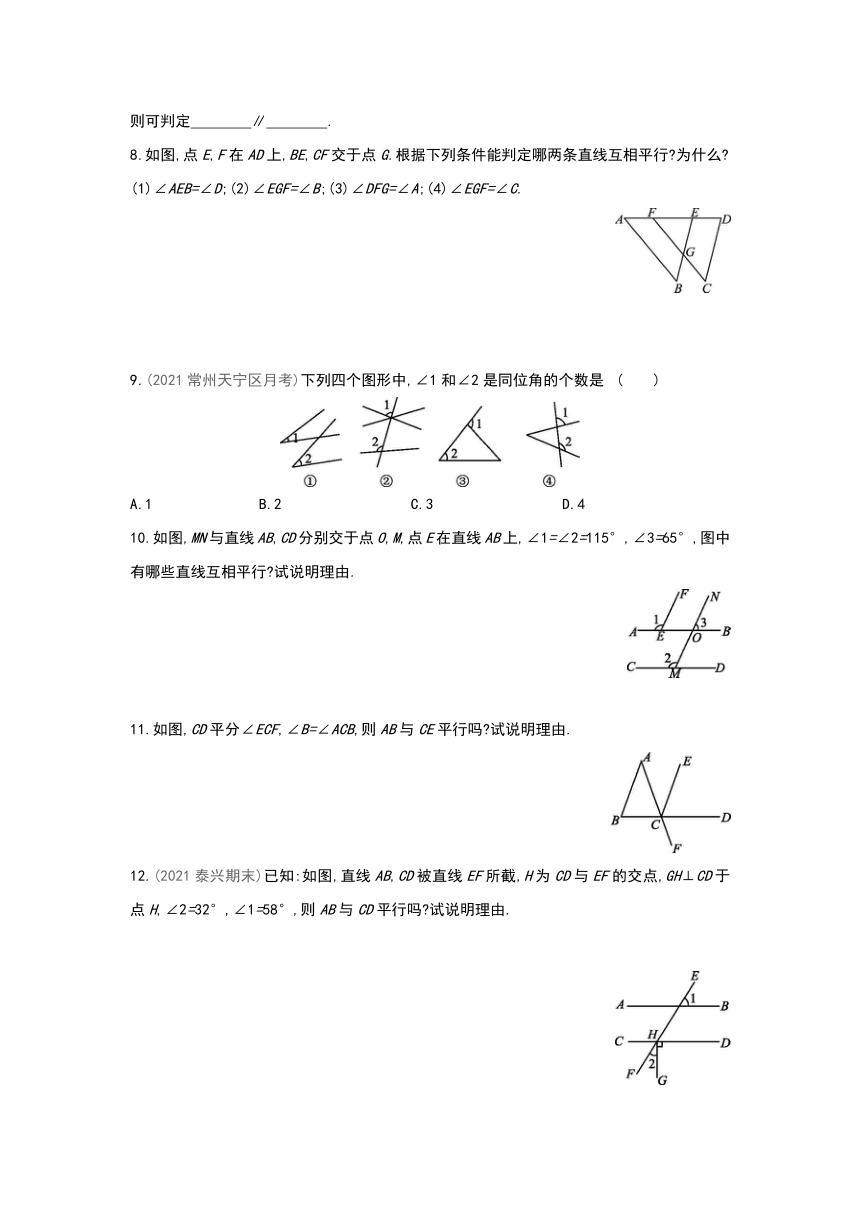
1.如图,直线AB,CD被直线EF所截,因为∠1与∠2都在直线EF的 侧,∠1在直线AB的 方,∠2在直线CD的 方,所以∠1与∠2是 角.
2.(2021苏州相城区期末)如图,直线a,b被直线c所截,与∠1是同位角的是 ( )
A.∠2 B.∠3 C.∠4 D.∠5
3.如图,∠B与 是直线 和直线 被直线 所截得的同位角.
4.如图,∠1与∠2是直线 , 被直线EF所截得的同位角,且∠1=∠2,根据“ ”得AB∥CD.
5.(2021徐州丰县月考)若∠1=∠2,则下列四个图形中,能够判定AB∥CD的是 ( )
6.如图,
因为∠ECD=∠B,
所以 ∥ ,
理由是 .
7.如图,点E在线段CD上,点F在线段AB上,G是线段AD的延长线上一点.
(1)若∠A=∠1,则可判定 ∥ ;
(2)若∠2=∠CDA,则可判定 ∥ ; (3)若∠B=∠AFE,则可判定 ∥ .
8.如图,点E,F在AD上,BE,CF交于点G.根据下列条件能判定哪两条直线互相平行 为什么
(1)∠AEB=∠D;(2)∠EGF=∠B;(3)∠DFG=∠A;(4)∠EGF=∠C.
9.(2021常州天宁区月考)下列四个图形中,∠1和∠2是同位角的个数是 ( )
A.1 B.2 C.3 D.4
10.如图,MN与直线AB,CD分别交于点O,M,点E在直线AB上,∠1=∠2=115°,∠3=65°,图中有哪些直线互相平行 试说明理由.
11.如图,CD平分∠ECF,∠B=∠ACB,则AB与CE平行吗 试说明理由.
12.(2021泰兴期末)已知:如图,直线AB,CD被直线EF所截,H为CD与EF的交点,GH⊥CD于点H,∠2=32°,∠1=58°,则AB与CD平行吗 试说明理由.
13.一辆货车在仓库装满货物准备运往超市,驶出仓库门口后开始向东行驶,途中向右拐了50°角,接着向前行驶,走了一段路程后,又向左拐了50°角,如图所示.
(1)此时货车的行驶方向和原来相同吗 请说明理由;
(2)如果货车第二次向左拐的角度是40°或70°,此时货车的行驶方向和原来相同吗 请说明理由.
14.对如图所示的四边形ABCD,你能用折纸的方法折出一条折痕MN,使MN∥BC吗 小明同学是这样做的:第一次折叠,使点C与点B重合,得折痕EF;第二次折叠,使点F与点E重合,得折痕MN,则MN即为所求.你觉得他的做法对吗 如果对,请说明理由.
7.1 第1课时 利用同位角探索两直线平行的条件
1.右 上 上 同位
2.A ∠2与∠1是同位角,∠3,∠4,∠5与∠1都不是同位角.
3.∠DAC BC AC DB
4.AB CD 同位角相等,两直线平行
5.C
6.EC AB 同位角相等,两直线平行
7.(1)AB CD (2)EF AD (3)BC EF
(1)因为∠A=∠1,根据“同位角相等,两直线平行”,可得AB∥CD;(2)因为∠2=∠CDA,根据“同位角相等,两直线平行”,可得EF∥AD;(3)因为∠B=∠AFE,根据“同位角相等,两直线平行”,可得BC∥EF.
8. 解决本题的关键是要确定相等的同位角是哪两条直线被哪一条直线所截得到的.
解:(1)BE∥CD.理由:因为∠AEB=∠D,根据“同位角相等,两直线平行”,可得BE∥CD.
(2)CF∥AB.理由:因为∠EGF=∠B,根据“同位角相等,两直线平行”,可得CF∥AB.
(3)CF∥AB.理由:因为∠DFG=∠A,根据“同位角相等,两直线平行”,可得CF∥AB.
(4)BE∥CD.理由:因为∠EGF=∠C,根据“同位角相等,两直线平行”,可得BE∥CD.
9.C 其中∠1和∠2是同位角的为图②③④,共3个.
10.解:EF∥MN,AB∥CD.
理由:由∠3=65°,可得到∠AON=115°,从而∠1=∠2=∠AON=115°,
再根据“同位角相等,两直线平行”,得到EF∥MN,AB∥CD.
11.解:AB∥CE.理由:
因为CD平分∠ECF,所以∠ECD=∠DCF.
因为∠ACB=∠DCF,所以∠ECD=∠ACB.
又因为∠B=∠ACB,所以∠B=∠ECD,所以AB∥CE.
12.解:AB∥CD.理由如下:
由GH⊥CD知∠CHG=90°,
又∠2=32°,
则∠CHF=90°-∠2=58°,
可得∠EHD=∠CHF=58°.
又因为∠1=58°,
所以∠1=∠EHD,
所以AB∥CD.
13.解:(1)货车的行驶方向和原来相同.理由如下:
如图,因为∠AOO'=∠A'O'B'=50°,根据“同位角相等,两直线平行”可得OA∥O'A',且货车两次都向东行驶,所以货车的行驶方向和原来相同.
(2)货车的行驶方向和原来不相同.理由如下:
因为第二次向左拐的角度是40°或70°,不是50°,即同位角不相等,所以两直线不平行,即O'A'不平行于OA,所以货车的行驶方向和原来不相同.
14.解:他的做法是对的.理由:设EF与MN交于点O,由两次折叠可知∠EON=∠EFC=90°,根据“同位角相等,两直线平行”,可得MN∥BC.
1.如图,直线AB,CD被直线EF所截,因为∠1与∠2都在直线EF的 侧,∠1在直线AB的 方,∠2在直线CD的 方,所以∠1与∠2是 角.
2.(2021苏州相城区期末)如图,直线a,b被直线c所截,与∠1是同位角的是 ( )
A.∠2 B.∠3 C.∠4 D.∠5
3.如图,∠B与 是直线 和直线 被直线 所截得的同位角.
4.如图,∠1与∠2是直线 , 被直线EF所截得的同位角,且∠1=∠2,根据“ ”得AB∥CD.
5.(2021徐州丰县月考)若∠1=∠2,则下列四个图形中,能够判定AB∥CD的是 ( )
6.如图,
因为∠ECD=∠B,
所以 ∥ ,
理由是 .
7.如图,点E在线段CD上,点F在线段AB上,G是线段AD的延长线上一点.
(1)若∠A=∠1,则可判定 ∥ ;
(2)若∠2=∠CDA,则可判定 ∥ ; (3)若∠B=∠AFE,则可判定 ∥ .
8.如图,点E,F在AD上,BE,CF交于点G.根据下列条件能判定哪两条直线互相平行 为什么
(1)∠AEB=∠D;(2)∠EGF=∠B;(3)∠DFG=∠A;(4)∠EGF=∠C.
9.(2021常州天宁区月考)下列四个图形中,∠1和∠2是同位角的个数是 ( )
A.1 B.2 C.3 D.4
10.如图,MN与直线AB,CD分别交于点O,M,点E在直线AB上,∠1=∠2=115°,∠3=65°,图中有哪些直线互相平行 试说明理由.
11.如图,CD平分∠ECF,∠B=∠ACB,则AB与CE平行吗 试说明理由.
12.(2021泰兴期末)已知:如图,直线AB,CD被直线EF所截,H为CD与EF的交点,GH⊥CD于点H,∠2=32°,∠1=58°,则AB与CD平行吗 试说明理由.
13.一辆货车在仓库装满货物准备运往超市,驶出仓库门口后开始向东行驶,途中向右拐了50°角,接着向前行驶,走了一段路程后,又向左拐了50°角,如图所示.
(1)此时货车的行驶方向和原来相同吗 请说明理由;
(2)如果货车第二次向左拐的角度是40°或70°,此时货车的行驶方向和原来相同吗 请说明理由.
14.对如图所示的四边形ABCD,你能用折纸的方法折出一条折痕MN,使MN∥BC吗 小明同学是这样做的:第一次折叠,使点C与点B重合,得折痕EF;第二次折叠,使点F与点E重合,得折痕MN,则MN即为所求.你觉得他的做法对吗 如果对,请说明理由.
7.1 第1课时 利用同位角探索两直线平行的条件
1.右 上 上 同位
2.A ∠2与∠1是同位角,∠3,∠4,∠5与∠1都不是同位角.
3.∠DAC BC AC DB
4.AB CD 同位角相等,两直线平行
5.C
6.EC AB 同位角相等,两直线平行
7.(1)AB CD (2)EF AD (3)BC EF
(1)因为∠A=∠1,根据“同位角相等,两直线平行”,可得AB∥CD;(2)因为∠2=∠CDA,根据“同位角相等,两直线平行”,可得EF∥AD;(3)因为∠B=∠AFE,根据“同位角相等,两直线平行”,可得BC∥EF.
8. 解决本题的关键是要确定相等的同位角是哪两条直线被哪一条直线所截得到的.
解:(1)BE∥CD.理由:因为∠AEB=∠D,根据“同位角相等,两直线平行”,可得BE∥CD.
(2)CF∥AB.理由:因为∠EGF=∠B,根据“同位角相等,两直线平行”,可得CF∥AB.
(3)CF∥AB.理由:因为∠DFG=∠A,根据“同位角相等,两直线平行”,可得CF∥AB.
(4)BE∥CD.理由:因为∠EGF=∠C,根据“同位角相等,两直线平行”,可得BE∥CD.
9.C 其中∠1和∠2是同位角的为图②③④,共3个.
10.解:EF∥MN,AB∥CD.
理由:由∠3=65°,可得到∠AON=115°,从而∠1=∠2=∠AON=115°,
再根据“同位角相等,两直线平行”,得到EF∥MN,AB∥CD.
11.解:AB∥CE.理由:
因为CD平分∠ECF,所以∠ECD=∠DCF.
因为∠ACB=∠DCF,所以∠ECD=∠ACB.
又因为∠B=∠ACB,所以∠B=∠ECD,所以AB∥CE.
12.解:AB∥CD.理由如下:
由GH⊥CD知∠CHG=90°,
又∠2=32°,
则∠CHF=90°-∠2=58°,
可得∠EHD=∠CHF=58°.
又因为∠1=58°,
所以∠1=∠EHD,
所以AB∥CD.
13.解:(1)货车的行驶方向和原来相同.理由如下:
如图,因为∠AOO'=∠A'O'B'=50°,根据“同位角相等,两直线平行”可得OA∥O'A',且货车两次都向东行驶,所以货车的行驶方向和原来相同.
(2)货车的行驶方向和原来不相同.理由如下:
因为第二次向左拐的角度是40°或70°,不是50°,即同位角不相等,所以两直线不平行,即O'A'不平行于OA,所以货车的行驶方向和原来不相同.
14.解:他的做法是对的.理由:设EF与MN交于点O,由两次折叠可知∠EON=∠EFC=90°,根据“同位角相等,两直线平行”,可得MN∥BC.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
