苏科版数学七年级下册 7.5 多边形的内角和 第2、3课时 同步课时训练(word版含解析)
文档属性
| 名称 | 苏科版数学七年级下册 7.5 多边形的内角和 第2、3课时 同步课时训练(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 150.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-04 00:00:00 | ||
图片预览


文档简介
第2课时 多边形的内角和
1.已知一个多边形的内角和为1080°,则这个多边形是 ( )
A.九边形 B.八边形 C.七边形 D.六边形
2.下列度数中,不可能是某个多边形的内角和的是 ( )
A.180° B.270° C.360° D.540°
3.(2020泰兴模拟)如图所示,∠B的度数为 ( )
A.85° B.95° C.105° D.115°
4.(2021淮安淮阴区月考)一个多边形的每个内角都是150°,那么这个多边形的边数为 .
图 图
5.(2020宿迁宿城区月考)如图,五边形ABCDE的每个内角都相等,分别过顶点D,E作一条射线,交点为H,如果CD∥EH,那么∠DEH= °.
6.如图,六边形ABCDEF的各个内角都相等,且∠DAB=60°.求∠ADE的度数.
图
7.已知一个多边形的每一个内角都等于135°,则这个多边形的对角线条数为 ( )
A.26 B.24 C.22 D.20
8.(2021苏州相城区月考)如图,六边形ABCDEF内部有一点G,连接BG,DG.若∠1+∠2+∠3+∠4+∠5=440°,则∠BGD的大小为 °.
图
9.(2021盐城亭湖区月考)一个多边形截去一个角后,所形成的一个新多边形的内角和为2520°,则原多边形有 条边.
10.如图,一块较为精密的模板中,AB,CD的延长线应该相交成80°的角,因交点不在模板上,不便测量,现测得∠BAE=124°,∠DCF=155°,AE⊥EF,CF⊥EF,此时AB,CD的延长线相交成的角是否符合规定 为什么
图
11.如图,∠1+∠2+∠3+∠4+∠5+∠6+∠7等于 ( )
A.450° B.540° C.630° D.720°
图
第3课时 多边形的外角和
1.十边形的外角和为 ( )
A.180° B.360° C.720° D.1440°
2.(2021南通如东县模拟)一个多边形每一个外角都等于18°,则这个多边形的边数为 ( )
A.10 B.12 C.16 D.20
3.(2021扬州模拟)若某多边形的边数增加1,则这个多边形的外角和 ( )
A.增加180° B.增加360°
C.减少180° D.不变
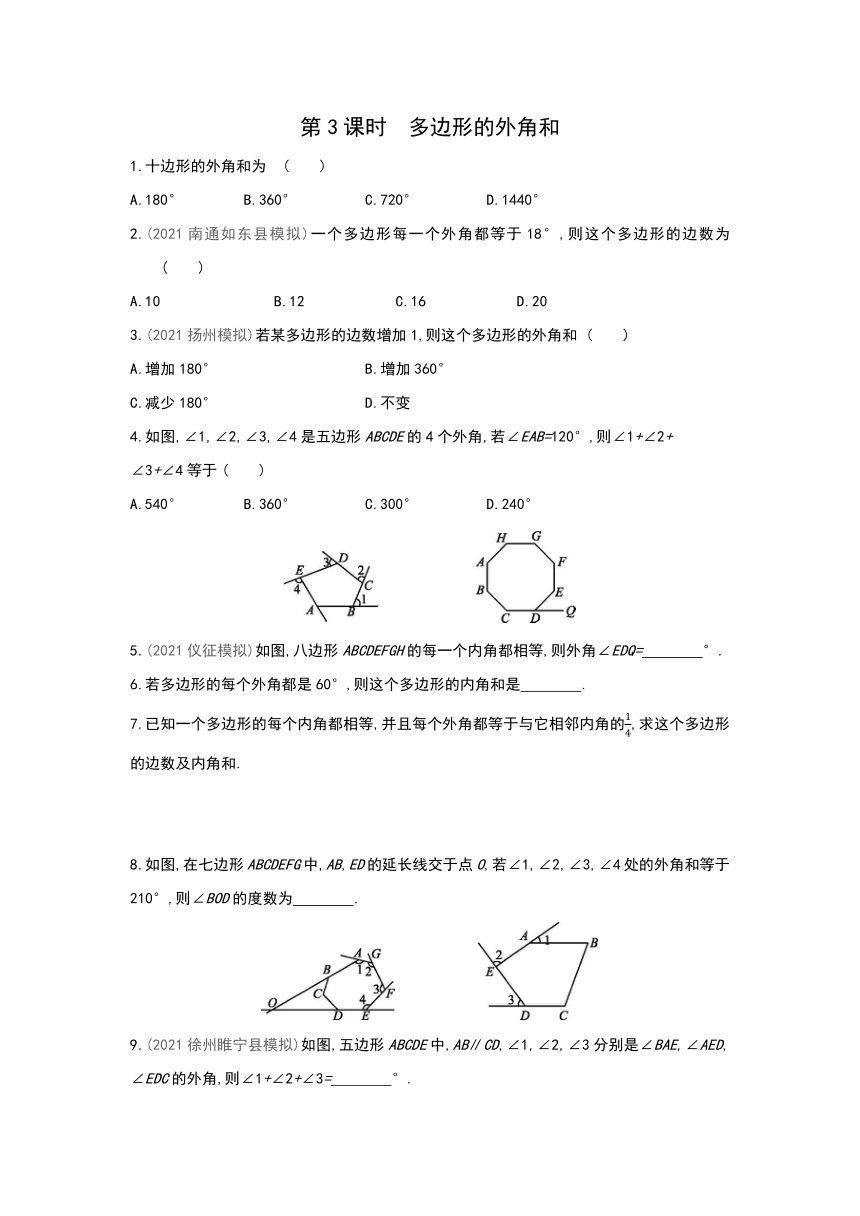
4.如图,∠1,∠2,∠3,∠4是五边形ABCDE的4个外角,若∠EAB=120°,则∠1+∠2+
∠3+∠4等于 ( )
A.540° B.360° C.300° D.240°
5.(2021仪征模拟)如图,八边形ABCDEFGH的每一个内角都相等,则外角∠EDQ= °.
6.若多边形的每个外角都是60°,则这个多边形的内角和是 .
7.已知一个多边形的每个内角都相等,并且每个外角都等于与它相邻内角的,求这个多边形的边数及内角和.
8.如图,在七边形ABCDEFG中,AB,ED的延长线交于点O,若∠1,∠2,∠3,∠4处的外角和等于210°,则∠BOD的度数为 .
9.(2021徐州睢宁县模拟)如图,五边形ABCDE中,AB∥CD,∠1,∠2,∠3分别是∠BAE,∠AED,∠EDC的外角,则∠1+∠2+∠3= °.
10.一个多边形的每个外角都相等,且比它的内角小140°,求它的边数和每个内角的度数.
11.已知一个多边形的所有内角与某一外角之和等于1350°,求这个多边形的边数.
第2课时 多边形的内角和
1.B 根据多边形的内角和公式,得(n-2)·180=1080,解得n=8,所以这个多边形的边数是8.故选B.
2.B 多边形的内角和是180°的整数倍.
3.D 五边形的内角和为(5-2)×180°=540°,
则∠A+∠B+∠C+∠D+∠E=540°,
故∠B=540°-∠A-∠C-∠D-∠E=540°-125°-60°-150°-90°=115°.
4.12 由题意可得180°·(n-2)=150°·n,
解得n=12.所以多边形是十二边形.
5.72 五边形的内角和为(5-2)×180°=540°,
则∠CDE=540°÷5=108°.
而CD∥EH,则∠DEH=180°-∠CDE=72°.
6.解:因为六边形ABCDEF的各个内角都相等,所以每个内角的度数为=120°,
所以∠FAB=∠F=∠E=120°.
因为∠DAB=60°,所以∠FAD=∠FAB-∠DAB=120°-60°=60°.
因为∠ADE+∠FAD+∠F+∠E=360°,
所以∠ADE=360°-∠FAD-∠F-∠E=360°-60°-120°-120°=60°.
7.D 设多边形的边数是n,则(n-2)·180°=135°n,解得n=8,
所以多边形的对角线的条数是==20.故选D.
8.80 由∠1+∠5+∠4+∠3+∠2+∠GBC+∠C+∠CDG=180°×(6-2)=720°,
及∠1+∠2+∠3+∠4+∠5=440°,得∠GBC+∠C+∠CDG=720°-440°=280°,
而多边形BCDG是四边形,
则∠C+∠GBC+∠CDG+∠BGD=360°,
所以∠BGD=360°-(∠GBC+∠C+∠CDG)=360°-280°=80°.
9.15或16或17 设新多边形的边数为n,则(n-2)·180°=2520°,解得n=16,
①若截去一个角后边数增加1,则原多边形边数为15,
②若截去一个角后边数不变,则原多边形边数为16,
③若截去一个角后边数减少1,则原多边形边数为17,故原多边形的边数可以为15或16或17.
10.解:不符合规定.
理由:设AB,CD的延长线交于点G,如图.
因为AE⊥EF,CF⊥EF,
所以∠E=∠F=90°.
因为∠BAE=124°,∠DCF=155°,
所以∠G=540°-(124°+155°+90°×2)=540°-459°=81°.
因为81°≠80°,
所以AB,CD的延长线相交成的角不符合规定.
11.B 如图,连接CD.
因为∠3+∠4=∠8+∠9,
所以∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+∠2+∠8+∠9+∠5+∠6+∠7=五边形ABCDE的内角和=540°.
故选B.
第3课时 多边形的外角和
1.B
2.D 由一个多边形的每一个外角都等于18°,且多边形的外角和等于360°,得这个多边形的边数是360°÷18°=20.
3.D 任意多边形的外角和都是360°,若某多边形的边数增加1,则这个多边形的外角和不变.
4.C 如图,由题意得∠5=180°-∠EAB=60°.又因为多边形的外角和为360°,
所以∠1+∠2+∠3+∠4=360°-∠5=300°.
故选C.
5.45 由八边形ABCDEFGH的每一个内角都相等,得每个外角的度数为360°÷8=45°,则∠EDQ的度数为45°.
6.720° 该多边形的边数为360°÷60°=6,该多边形的内角和为(6-2)×180°=720°.
7.解:设这个多边形的一个外角的度数为x.由题意,得x=(180°-x),解得x=36°,则多边形的边数为360÷36=10,多边形的内角和为(10-2)×180°=1440°,即多边形为十边形,内角和为1440°.
8.30° 因为∠1,∠2,∠3,∠4处的外角的度数之和为210°,
所以∠1+∠2+∠3+∠4+210°=4×180°,所以∠1+∠2+∠3+∠4=510°.
因为五边形OAGFE的内角和=(5-2)×180°=540°,
所以∠1+∠2+∠3+∠4+∠BOD=540°,所以∠BOD=540°-510°=30°.
9.180 由AB∥CD,得∠B+∠C=180°.
因为∠EAB+∠AED+∠EDC+∠C+∠B=(5-2)×180°,
所以(180°-∠1)+(180°-∠2)+(180°-∠3)+∠B+∠C=540°,所以∠1+∠2+∠3=180°.
10.解:设每个内角的度数为n°,则每个外角的度数为(n-140)°.
由n+(n-140)=180,得n=160.
即每个内角的度数为160°,则每个外角的度数为20°.
因为360÷20=18,所以这个多边形的边数为18.
11.解:设这个多边形的边数为n,这个外角为x,则0°由题意,得(n-2)·180°+x=1350°,
解得n=.
因为n为整数,
所以1710°-x必为180°的倍数,
又因为0°故这个多边形的边数是9.
1.已知一个多边形的内角和为1080°,则这个多边形是 ( )
A.九边形 B.八边形 C.七边形 D.六边形
2.下列度数中,不可能是某个多边形的内角和的是 ( )
A.180° B.270° C.360° D.540°
3.(2020泰兴模拟)如图所示,∠B的度数为 ( )
A.85° B.95° C.105° D.115°
4.(2021淮安淮阴区月考)一个多边形的每个内角都是150°,那么这个多边形的边数为 .
图 图
5.(2020宿迁宿城区月考)如图,五边形ABCDE的每个内角都相等,分别过顶点D,E作一条射线,交点为H,如果CD∥EH,那么∠DEH= °.
6.如图,六边形ABCDEF的各个内角都相等,且∠DAB=60°.求∠ADE的度数.
图
7.已知一个多边形的每一个内角都等于135°,则这个多边形的对角线条数为 ( )
A.26 B.24 C.22 D.20
8.(2021苏州相城区月考)如图,六边形ABCDEF内部有一点G,连接BG,DG.若∠1+∠2+∠3+∠4+∠5=440°,则∠BGD的大小为 °.
图
9.(2021盐城亭湖区月考)一个多边形截去一个角后,所形成的一个新多边形的内角和为2520°,则原多边形有 条边.
10.如图,一块较为精密的模板中,AB,CD的延长线应该相交成80°的角,因交点不在模板上,不便测量,现测得∠BAE=124°,∠DCF=155°,AE⊥EF,CF⊥EF,此时AB,CD的延长线相交成的角是否符合规定 为什么
图
11.如图,∠1+∠2+∠3+∠4+∠5+∠6+∠7等于 ( )
A.450° B.540° C.630° D.720°
图
第3课时 多边形的外角和
1.十边形的外角和为 ( )
A.180° B.360° C.720° D.1440°
2.(2021南通如东县模拟)一个多边形每一个外角都等于18°,则这个多边形的边数为 ( )
A.10 B.12 C.16 D.20
3.(2021扬州模拟)若某多边形的边数增加1,则这个多边形的外角和 ( )
A.增加180° B.增加360°
C.减少180° D.不变
4.如图,∠1,∠2,∠3,∠4是五边形ABCDE的4个外角,若∠EAB=120°,则∠1+∠2+
∠3+∠4等于 ( )
A.540° B.360° C.300° D.240°
5.(2021仪征模拟)如图,八边形ABCDEFGH的每一个内角都相等,则外角∠EDQ= °.
6.若多边形的每个外角都是60°,则这个多边形的内角和是 .
7.已知一个多边形的每个内角都相等,并且每个外角都等于与它相邻内角的,求这个多边形的边数及内角和.
8.如图,在七边形ABCDEFG中,AB,ED的延长线交于点O,若∠1,∠2,∠3,∠4处的外角和等于210°,则∠BOD的度数为 .
9.(2021徐州睢宁县模拟)如图,五边形ABCDE中,AB∥CD,∠1,∠2,∠3分别是∠BAE,∠AED,∠EDC的外角,则∠1+∠2+∠3= °.
10.一个多边形的每个外角都相等,且比它的内角小140°,求它的边数和每个内角的度数.
11.已知一个多边形的所有内角与某一外角之和等于1350°,求这个多边形的边数.
第2课时 多边形的内角和
1.B 根据多边形的内角和公式,得(n-2)·180=1080,解得n=8,所以这个多边形的边数是8.故选B.
2.B 多边形的内角和是180°的整数倍.
3.D 五边形的内角和为(5-2)×180°=540°,
则∠A+∠B+∠C+∠D+∠E=540°,
故∠B=540°-∠A-∠C-∠D-∠E=540°-125°-60°-150°-90°=115°.
4.12 由题意可得180°·(n-2)=150°·n,
解得n=12.所以多边形是十二边形.
5.72 五边形的内角和为(5-2)×180°=540°,
则∠CDE=540°÷5=108°.
而CD∥EH,则∠DEH=180°-∠CDE=72°.
6.解:因为六边形ABCDEF的各个内角都相等,所以每个内角的度数为=120°,
所以∠FAB=∠F=∠E=120°.
因为∠DAB=60°,所以∠FAD=∠FAB-∠DAB=120°-60°=60°.
因为∠ADE+∠FAD+∠F+∠E=360°,
所以∠ADE=360°-∠FAD-∠F-∠E=360°-60°-120°-120°=60°.
7.D 设多边形的边数是n,则(n-2)·180°=135°n,解得n=8,
所以多边形的对角线的条数是==20.故选D.
8.80 由∠1+∠5+∠4+∠3+∠2+∠GBC+∠C+∠CDG=180°×(6-2)=720°,
及∠1+∠2+∠3+∠4+∠5=440°,得∠GBC+∠C+∠CDG=720°-440°=280°,
而多边形BCDG是四边形,
则∠C+∠GBC+∠CDG+∠BGD=360°,
所以∠BGD=360°-(∠GBC+∠C+∠CDG)=360°-280°=80°.
9.15或16或17 设新多边形的边数为n,则(n-2)·180°=2520°,解得n=16,
①若截去一个角后边数增加1,则原多边形边数为15,
②若截去一个角后边数不变,则原多边形边数为16,
③若截去一个角后边数减少1,则原多边形边数为17,故原多边形的边数可以为15或16或17.
10.解:不符合规定.
理由:设AB,CD的延长线交于点G,如图.
因为AE⊥EF,CF⊥EF,
所以∠E=∠F=90°.
因为∠BAE=124°,∠DCF=155°,
所以∠G=540°-(124°+155°+90°×2)=540°-459°=81°.
因为81°≠80°,
所以AB,CD的延长线相交成的角不符合规定.
11.B 如图,连接CD.
因为∠3+∠4=∠8+∠9,
所以∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+∠2+∠8+∠9+∠5+∠6+∠7=五边形ABCDE的内角和=540°.
故选B.
第3课时 多边形的外角和
1.B
2.D 由一个多边形的每一个外角都等于18°,且多边形的外角和等于360°,得这个多边形的边数是360°÷18°=20.
3.D 任意多边形的外角和都是360°,若某多边形的边数增加1,则这个多边形的外角和不变.
4.C 如图,由题意得∠5=180°-∠EAB=60°.又因为多边形的外角和为360°,
所以∠1+∠2+∠3+∠4=360°-∠5=300°.
故选C.
5.45 由八边形ABCDEFGH的每一个内角都相等,得每个外角的度数为360°÷8=45°,则∠EDQ的度数为45°.
6.720° 该多边形的边数为360°÷60°=6,该多边形的内角和为(6-2)×180°=720°.
7.解:设这个多边形的一个外角的度数为x.由题意,得x=(180°-x),解得x=36°,则多边形的边数为360÷36=10,多边形的内角和为(10-2)×180°=1440°,即多边形为十边形,内角和为1440°.
8.30° 因为∠1,∠2,∠3,∠4处的外角的度数之和为210°,
所以∠1+∠2+∠3+∠4+210°=4×180°,所以∠1+∠2+∠3+∠4=510°.
因为五边形OAGFE的内角和=(5-2)×180°=540°,
所以∠1+∠2+∠3+∠4+∠BOD=540°,所以∠BOD=540°-510°=30°.
9.180 由AB∥CD,得∠B+∠C=180°.
因为∠EAB+∠AED+∠EDC+∠C+∠B=(5-2)×180°,
所以(180°-∠1)+(180°-∠2)+(180°-∠3)+∠B+∠C=540°,所以∠1+∠2+∠3=180°.
10.解:设每个内角的度数为n°,则每个外角的度数为(n-140)°.
由n+(n-140)=180,得n=160.
即每个内角的度数为160°,则每个外角的度数为20°.
因为360÷20=18,所以这个多边形的边数为18.
11.解:设这个多边形的边数为n,这个外角为x,则0°
解得n=.
因为n为整数,
所以1710°-x必为180°的倍数,
又因为0°
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
