苏科版数学七年级下册同步课时训练:7.5.1三角形的内角和(word版含答案)
文档属性
| 名称 | 苏科版数学七年级下册同步课时训练:7.5.1三角形的内角和(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 143.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-04 00:00:00 | ||
图片预览



文档简介
7.5 第1课时 三角形的内角和
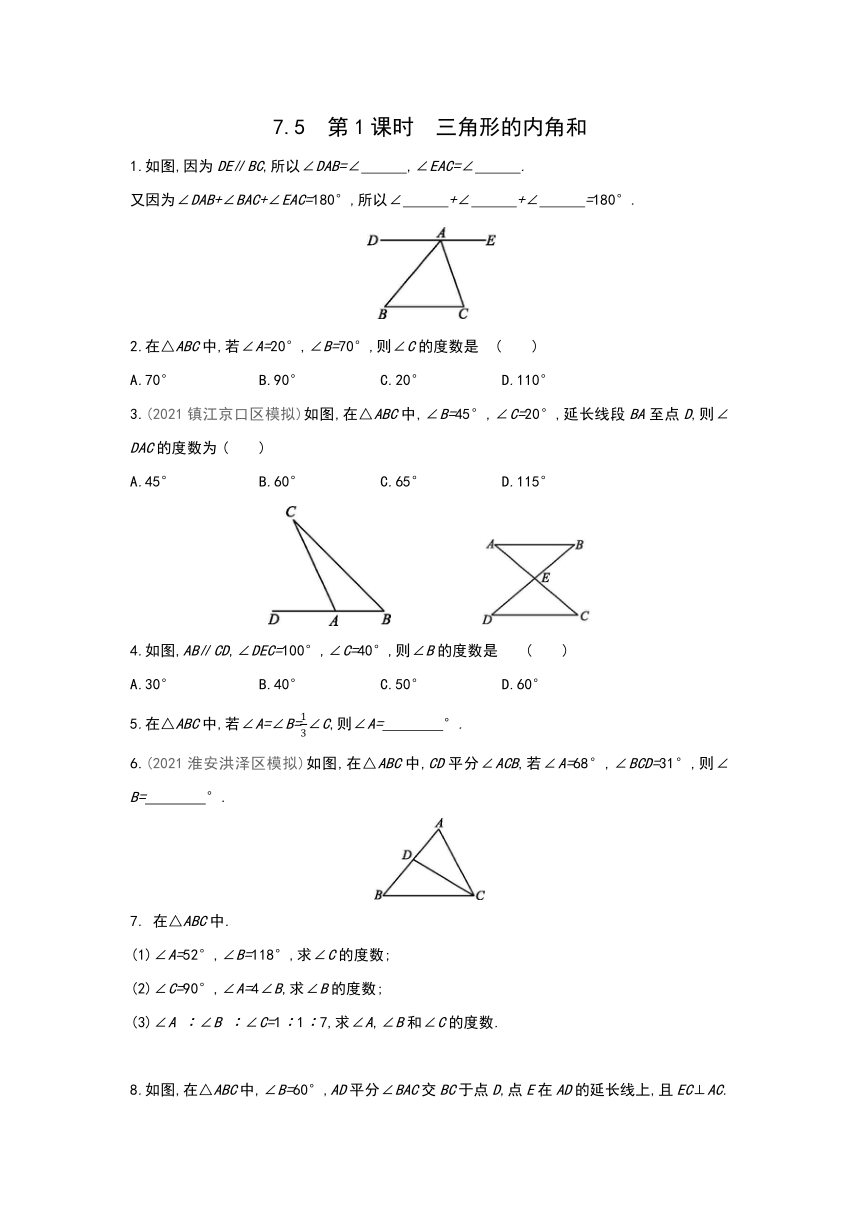
1.如图,因为DE∥BC,所以∠DAB=∠ ,∠EAC=∠ .
又因为∠DAB+∠BAC+∠EAC=180°,所以∠ +∠ +∠ =180°.
2.在△ABC中,若∠A=20°,∠B=70°,则∠C的度数是 ( )
A.70° B.90° C.20° D.110°
3.(2021镇江京口区模拟)如图,在△ABC中,∠B=45°,∠C=20°,延长线段BA至点D,则∠DAC的度数为 ( )
A.45° B.60° C.65° D.115°
4.如图,AB∥CD,∠DEC=100°,∠C=40°,则∠B的度数是 ( )
A.30° B.40° C.50° D.60°
5.在△ABC中,若∠A=∠B=∠C,则∠A= °.
6.(2021淮安洪泽区模拟)如图,在△ABC中,CD平分∠ACB,若∠A=68°,∠BCD=31°,则∠B= °.
7. 在△ABC中.
(1)∠A=52°,∠B=118°,求∠C的度数;
(2)∠C=90°,∠A=4∠B,求∠B的度数;
(3)∠A ∶∠B ∶∠C=1∶1∶7,求∠A,∠B和∠C的度数.
8.如图,在△ABC中,∠B=60°,AD平分∠BAC交BC于点D,点E在AD的延长线上,且EC⊥AC.若∠E=50°,则∠ADC的度数是 .
9.如图,将一块三角尺DEF放置在锐角三角形ABC上,使得该三角尺的两条直角边DE,DF恰好分别经过点B,C.若∠A=50°,则∠ABD+∠ACD= °.
10.(教材例2变式)(2021兴化月考)如图,△ABC的角平分线BD,CE交于点P.
(1)若∠ABC=60°,∠ACB=80°,求∠BPC的度数;
(2)若∠A=α,求∠BPC的度数(用含α的代数式表示).
11.(2021徐州期末改编)如图①,在△ABC中,∠C=70°,D,E分别是AC,BC边上的点,P是AB边上一动点.
(1)试探究∠α,∠1,∠2间的数量关系,并说明理由.
(2)如图②,若点P在边AB的延长线上,则(1)中结论是否改变 为什么
12、如图,把△ABC沿线段DE折叠,使点A落在点F处,BC∥DE,若∠A+∠B=105°,则∠FEC= °.
13、如图,把△ABC沿线段DE折叠,使点A落在点F处,BC∥DE,若∠A+∠B=65°,则∠FEC= °.
14、如图,在△ABC中,∠A=80°,∠B=70°,D是AC边上一点,过点D将△ABC折叠,使点C落在BC下方的点C'处,折痕DE与BC交于点E,当AB与∠C'的一边平行时,∠DEC'的度数为 .
7.5 第1课时 三角形的内角和
1.B C B BAC C
2.B
3.C ∠DAC=180°-∠CAB=180°-(180°-∠C-∠B)=∠C+∠B=45°+20°=65°.
4.B 依据三角形内角和是180°,可得∠D=40°,
再根据平行线的性质,即可得到∠B=∠D=40°.
5.36 设∠A=∠B=x,则∠C=3x.
因为∠A+∠B+∠C=180°,
所以x+x+3x=180°,解得x=36°,即∠A=36°.
6.50 由CD平分∠ACB,得∠ACB=2∠BCD=62°,则∠B=180°-∠A-∠ACB=50°.
7.解:(1)∠C=180°-∠A-∠B=10°.
(2)因为∠C=90°,所以∠A+∠B=180°-∠C=90°.
因为∠A=4∠B,所以4∠B+∠B=90°,所以∠B=18°.
(3)设∠A=x,则∠B=x,∠C=7x.根据题意,得x+x+7x=180°,解得x=20°,
所以∠A=20°,∠B=20°,∠C=140°.
8.100° 因为EC⊥AC,∠E=50°,所以∠DAC=40°.
因为AD平分∠BAC,所以∠BAD=∠DAC=40°.
因为∠B=60°,所以∠ADB=180°-40°-60°=80°,所以∠ADC=100°.
9.40 在△ABC中,因为∠A=50°,所以∠ABC+∠ACB=180°-50°=130°.
在△DBC中,因为∠BDC=90°,所以∠DBC+∠DCB=180°-90°=90°,
所以∠ABD+∠ACD=130°-90°=40°.
10.解:(1)由BD,CE为△ABC的角平分线,∠ABC=60°,∠ACB=80°,
得∠PBC=∠ABC=30°,∠PCB=∠ACB=40°,
则∠BPC=180°-∠PBC-∠PCB=110°.
(2)由BD,CE为△ABC的角平分线,
得∠PBC=∠ABC,∠PCB=∠ACB,
而∠ABC+∠ACB=180°-∠A,
则∠ABC+∠ACB=(180°-∠A)=90°-∠A,
即∠PBC+∠PCB=90°-∠A.
又∠BPC+∠PBC+∠PCB=180°,
所以∠BPC=180°-(∠PBC+∠PCB)=180°-90°-∠A=90°+∠A=90°+α.
11.解:(1)∠1+∠2=70°+∠α.理由如下:
如图,连接PC.
在△DPC中,由∠1=180°-∠CDP,∠DCP+∠DPC=180°-∠CDP,
得∠1=∠DCP+∠DPC.
同理可得∠2=∠ECP+∠CPE,
则∠1+∠2=∠DCP+∠DPC+∠ECP+∠CPE=∠ACB+∠DPE=∠ACB+∠α.
而∠ACB=70°,
于是∠1+∠2=70°+∠α.
(2)改变.理由如下:
在△CDF中,由∠1=180°-∠CDF,∠C+∠DFC=180°-∠CDF,
得∠1=∠C+∠CFD,
同理可得∠CFD=∠2+∠α,
则有∠1=∠C+∠2+∠α.
即∠1-∠2=70°+∠α.
12、 30 由∠A+∠B=105°,得∠C=180°-(∠A+∠B)=75°.
因为BC∥DE,所以∠AED=∠C=75°.
又△DEF由△DEA沿线段DE折叠而得,则∠DEF=∠AED=75°.
可得∠FEC=180°-∠AED-∠DEF=30°.
13、 50 由∠A+∠B=65°,得∠C=180°-(∠A+∠B)=115°.
因为BC∥DE,所以∠AED=∠C=115°.
又△DEF由△DEA沿线段DE折叠而得,则∠DEF=∠AED=115°.
可得∠DEC=180°-∠AED=65°.从而∠FEC=∠DEF-∠DEC=50°.
14、 110°或125° 由∠A=80°,∠B=70°,得∠C=180°-∠A-∠B=30°.
①当AB∥C'D时,∠CDC'=∠A=80°,
由折叠的性质得∠CDE=∠C'DE=∠CDC'=40°,∠C=∠C'=30°,
则∠DEC'=180°-∠C'DE-∠C'=110°.
②当AB∥C'E时,∠B=∠BEC'=70°,
由折叠的性质得∠CED=∠C'ED,
设∠CED=∠C'ED=x,
则x+x-70°=180°,解得x=125°,
则∠DEC'=125°.
1.如图,因为DE∥BC,所以∠DAB=∠ ,∠EAC=∠ .
又因为∠DAB+∠BAC+∠EAC=180°,所以∠ +∠ +∠ =180°.
2.在△ABC中,若∠A=20°,∠B=70°,则∠C的度数是 ( )
A.70° B.90° C.20° D.110°
3.(2021镇江京口区模拟)如图,在△ABC中,∠B=45°,∠C=20°,延长线段BA至点D,则∠DAC的度数为 ( )
A.45° B.60° C.65° D.115°
4.如图,AB∥CD,∠DEC=100°,∠C=40°,则∠B的度数是 ( )
A.30° B.40° C.50° D.60°
5.在△ABC中,若∠A=∠B=∠C,则∠A= °.
6.(2021淮安洪泽区模拟)如图,在△ABC中,CD平分∠ACB,若∠A=68°,∠BCD=31°,则∠B= °.
7. 在△ABC中.
(1)∠A=52°,∠B=118°,求∠C的度数;
(2)∠C=90°,∠A=4∠B,求∠B的度数;
(3)∠A ∶∠B ∶∠C=1∶1∶7,求∠A,∠B和∠C的度数.
8.如图,在△ABC中,∠B=60°,AD平分∠BAC交BC于点D,点E在AD的延长线上,且EC⊥AC.若∠E=50°,则∠ADC的度数是 .
9.如图,将一块三角尺DEF放置在锐角三角形ABC上,使得该三角尺的两条直角边DE,DF恰好分别经过点B,C.若∠A=50°,则∠ABD+∠ACD= °.
10.(教材例2变式)(2021兴化月考)如图,△ABC的角平分线BD,CE交于点P.
(1)若∠ABC=60°,∠ACB=80°,求∠BPC的度数;
(2)若∠A=α,求∠BPC的度数(用含α的代数式表示).
11.(2021徐州期末改编)如图①,在△ABC中,∠C=70°,D,E分别是AC,BC边上的点,P是AB边上一动点.
(1)试探究∠α,∠1,∠2间的数量关系,并说明理由.
(2)如图②,若点P在边AB的延长线上,则(1)中结论是否改变 为什么
12、如图,把△ABC沿线段DE折叠,使点A落在点F处,BC∥DE,若∠A+∠B=105°,则∠FEC= °.
13、如图,把△ABC沿线段DE折叠,使点A落在点F处,BC∥DE,若∠A+∠B=65°,则∠FEC= °.
14、如图,在△ABC中,∠A=80°,∠B=70°,D是AC边上一点,过点D将△ABC折叠,使点C落在BC下方的点C'处,折痕DE与BC交于点E,当AB与∠C'的一边平行时,∠DEC'的度数为 .
7.5 第1课时 三角形的内角和
1.B C B BAC C
2.B
3.C ∠DAC=180°-∠CAB=180°-(180°-∠C-∠B)=∠C+∠B=45°+20°=65°.
4.B 依据三角形内角和是180°,可得∠D=40°,
再根据平行线的性质,即可得到∠B=∠D=40°.
5.36 设∠A=∠B=x,则∠C=3x.
因为∠A+∠B+∠C=180°,
所以x+x+3x=180°,解得x=36°,即∠A=36°.
6.50 由CD平分∠ACB,得∠ACB=2∠BCD=62°,则∠B=180°-∠A-∠ACB=50°.
7.解:(1)∠C=180°-∠A-∠B=10°.
(2)因为∠C=90°,所以∠A+∠B=180°-∠C=90°.
因为∠A=4∠B,所以4∠B+∠B=90°,所以∠B=18°.
(3)设∠A=x,则∠B=x,∠C=7x.根据题意,得x+x+7x=180°,解得x=20°,
所以∠A=20°,∠B=20°,∠C=140°.
8.100° 因为EC⊥AC,∠E=50°,所以∠DAC=40°.
因为AD平分∠BAC,所以∠BAD=∠DAC=40°.
因为∠B=60°,所以∠ADB=180°-40°-60°=80°,所以∠ADC=100°.
9.40 在△ABC中,因为∠A=50°,所以∠ABC+∠ACB=180°-50°=130°.
在△DBC中,因为∠BDC=90°,所以∠DBC+∠DCB=180°-90°=90°,
所以∠ABD+∠ACD=130°-90°=40°.
10.解:(1)由BD,CE为△ABC的角平分线,∠ABC=60°,∠ACB=80°,
得∠PBC=∠ABC=30°,∠PCB=∠ACB=40°,
则∠BPC=180°-∠PBC-∠PCB=110°.
(2)由BD,CE为△ABC的角平分线,
得∠PBC=∠ABC,∠PCB=∠ACB,
而∠ABC+∠ACB=180°-∠A,
则∠ABC+∠ACB=(180°-∠A)=90°-∠A,
即∠PBC+∠PCB=90°-∠A.
又∠BPC+∠PBC+∠PCB=180°,
所以∠BPC=180°-(∠PBC+∠PCB)=180°-90°-∠A=90°+∠A=90°+α.
11.解:(1)∠1+∠2=70°+∠α.理由如下:
如图,连接PC.
在△DPC中,由∠1=180°-∠CDP,∠DCP+∠DPC=180°-∠CDP,
得∠1=∠DCP+∠DPC.
同理可得∠2=∠ECP+∠CPE,
则∠1+∠2=∠DCP+∠DPC+∠ECP+∠CPE=∠ACB+∠DPE=∠ACB+∠α.
而∠ACB=70°,
于是∠1+∠2=70°+∠α.
(2)改变.理由如下:
在△CDF中,由∠1=180°-∠CDF,∠C+∠DFC=180°-∠CDF,
得∠1=∠C+∠CFD,
同理可得∠CFD=∠2+∠α,
则有∠1=∠C+∠2+∠α.
即∠1-∠2=70°+∠α.
12、 30 由∠A+∠B=105°,得∠C=180°-(∠A+∠B)=75°.
因为BC∥DE,所以∠AED=∠C=75°.
又△DEF由△DEA沿线段DE折叠而得,则∠DEF=∠AED=75°.
可得∠FEC=180°-∠AED-∠DEF=30°.
13、 50 由∠A+∠B=65°,得∠C=180°-(∠A+∠B)=115°.
因为BC∥DE,所以∠AED=∠C=115°.
又△DEF由△DEA沿线段DE折叠而得,则∠DEF=∠AED=115°.
可得∠DEC=180°-∠AED=65°.从而∠FEC=∠DEF-∠DEC=50°.
14、 110°或125° 由∠A=80°,∠B=70°,得∠C=180°-∠A-∠B=30°.
①当AB∥C'D时,∠CDC'=∠A=80°,
由折叠的性质得∠CDE=∠C'DE=∠CDC'=40°,∠C=∠C'=30°,
则∠DEC'=180°-∠C'DE-∠C'=110°.
②当AB∥C'E时,∠B=∠BEC'=70°,
由折叠的性质得∠CED=∠C'ED,
设∠CED=∠C'ED=x,
则x+x-70°=180°,解得x=125°,
则∠DEC'=125°.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
