苏科版八年级数学下册 第9章 中心对称图形——平行四边形小结与思考 教案
文档属性
| 名称 | 苏科版八年级数学下册 第9章 中心对称图形——平行四边形小结与思考 教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 92.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-04 17:03:23 | ||
图片预览


文档简介
教案
课 题 第九章小结与思考(3) 课时安排 本章节第 3 课时
课 型 复习课 本章节共3 课时
教 学 目 标 1经历图形旋转变化中认识平面图形的性质的过程,体会数学的运用价值. 2、感受数学源于实践,又应用于实践,增强运用数学的意识,提高运用代数方法解决问题的能力,丰富数学活动的经验,拓展思维水平.
教学重点 寻找旋转问题题眼的方法。
教学难点 寻找旋转问题题眼的方法。
教学内容及过程 二次备课
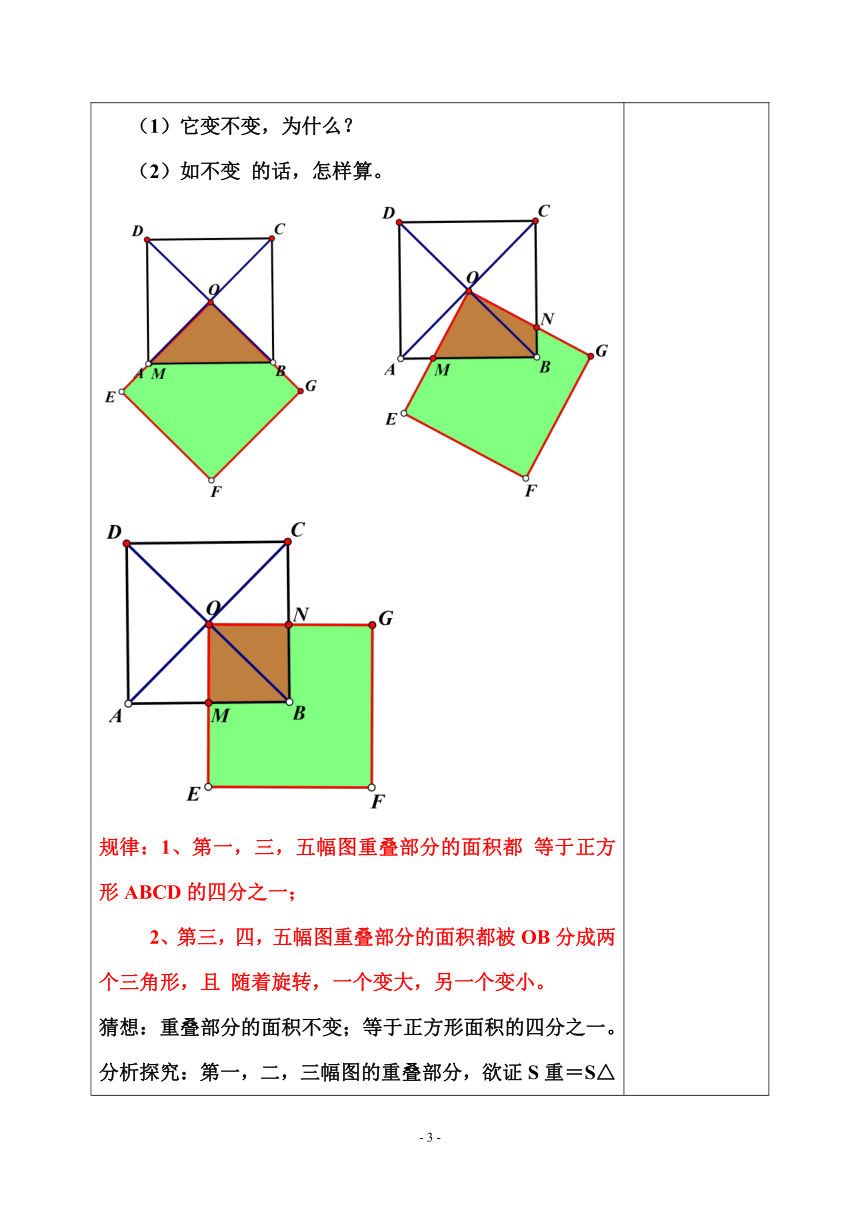
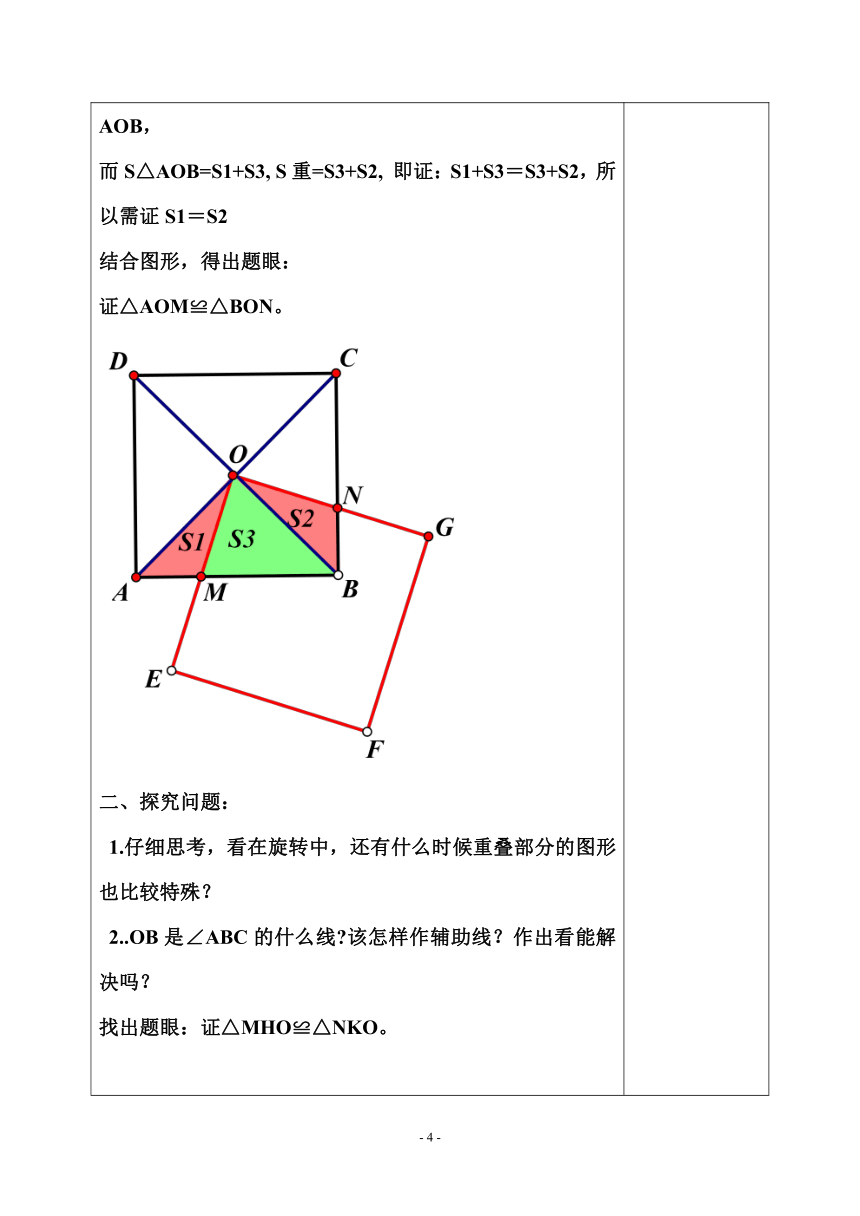
尝试与交流 已知:如图所示,两个正方形边长都为4,其中 正方形OEFG以正方形ABCD的对角线交点O 为中心进行旋转。 (1) 两个正方形的重叠部分的面积S会变化 吗?若变就说明理由,如不变,求 出重叠部分的面积。 (2)在旋转中,当边AB与边OE交于点M, 边BC与 边OG交于点N时,△MBN周长y会变化吗?若不 变说明理由,若要变,请求出它的范围。 此题比较抽象,学生理解起来很困难,关键在于根据旋转变化,抓住特殊点,化动为静,找出题眼。 对于第一问 ,难点在暴露重叠部分面积等于正方形面积的四分之一的思维过程,用过程找题眼(证全等),从而学习方法;若直接告知学生证全等,再去分析不变的原因,这样虽然省力,但不能举一反三,学生学不到方法。 对于第二问,关键在于表示三角形△MBN周长时,发现MB+BN=4,得出y=4+MN,转化为求MN的范围。 基于以上的分析,第一问实行启发式教学,让学生充分感受旋转的过程,总结规律,找出题眼,学习解决问题的方法;第二问分层进行,能力强的用第一问的方法,自己探究,寻找题眼;有困难的根据提纲进行,老师适时指导。 首先,整体感知已知是什么: 1.两个正方形, 2.边长为4,3.旋转。其次, 明确做什么:重叠部分的面积S, (1)它变不变,为什么? (2)如不变 的话,怎样算。 规律:1、第一,三,五幅图重叠部分的面积都 等于正方形ABCD的四分之一; 2、第三,四,五幅图重叠部分的面积都被OB分成两个三角形,且 随着旋转,一个变大,另一个变小。 猜想:重叠部分的面积不变;等于正方形面积的四分之一。 分析探究:第一,二,三幅图的重叠部分,欲证S重=S△AOB, 而S△AOB=S1+S3, S重=S3+S2, 即证:S1+S3=S3+S2,所以需证S1=S2 结合图形,得出题眼: 证△AOM≌△BON。 二、探究问题: 1.仔细思考,看在旋转中,还有什么时候重叠部分的图形也比较特殊? 2..OB是∠ABC的什么线 该怎样作辅助线?作出看能解决吗? 找出题眼:证△MHO≌△NKO。 三、规律总结: 这类运动类问题以后你们该怎样入手? 一、题图结合,明确问题; 二、想象运动,分析规律; 三、作出猜想,找出题眼; 四、理顺关系,完成答题。 A 组同学直接按刚才的方法思考第2。 B 组的同学先独立思考,有问题的按下列提纲提示进行。 一、题图结合,明确问题;三角形NBM的周长(y=BM+BN+MN)变不变及范 围问题。 二、想象运动,分析规律; BM逐渐变小,BN逐渐变大,但,BM+BN=4 , 但MN由大逐渐到小,到最小又逐渐到大。 三、作出猜想,找出题眼; 因为 y=4+MN ,所以线段MN的取值范围就是题眼。 思考: (1) MN最长接近多少,能等于它吗? (2)MN有最小值,为多少? 当MN最小时,两种情况下M点在AB的位置一样吗? 四:拓展思维 已知:如图所示,两个正方形边长都为4,其中正方形OEFG以正方形ABCD的对角线交点O为中心进行旋转。 1. 求△MBN的最大面积。 2. 两个正方形的重叠部分的周长 会变 化吗?为什么? 3. 求DF的范围。 4. 当∠AOE=30°时,求AM的长。 六、课后作业 见作业纸
- 1 -
课 题 第九章小结与思考(3) 课时安排 本章节第 3 课时
课 型 复习课 本章节共3 课时
教 学 目 标 1经历图形旋转变化中认识平面图形的性质的过程,体会数学的运用价值. 2、感受数学源于实践,又应用于实践,增强运用数学的意识,提高运用代数方法解决问题的能力,丰富数学活动的经验,拓展思维水平.
教学重点 寻找旋转问题题眼的方法。
教学难点 寻找旋转问题题眼的方法。
教学内容及过程 二次备课
尝试与交流 已知:如图所示,两个正方形边长都为4,其中 正方形OEFG以正方形ABCD的对角线交点O 为中心进行旋转。 (1) 两个正方形的重叠部分的面积S会变化 吗?若变就说明理由,如不变,求 出重叠部分的面积。 (2)在旋转中,当边AB与边OE交于点M, 边BC与 边OG交于点N时,△MBN周长y会变化吗?若不 变说明理由,若要变,请求出它的范围。 此题比较抽象,学生理解起来很困难,关键在于根据旋转变化,抓住特殊点,化动为静,找出题眼。 对于第一问 ,难点在暴露重叠部分面积等于正方形面积的四分之一的思维过程,用过程找题眼(证全等),从而学习方法;若直接告知学生证全等,再去分析不变的原因,这样虽然省力,但不能举一反三,学生学不到方法。 对于第二问,关键在于表示三角形△MBN周长时,发现MB+BN=4,得出y=4+MN,转化为求MN的范围。 基于以上的分析,第一问实行启发式教学,让学生充分感受旋转的过程,总结规律,找出题眼,学习解决问题的方法;第二问分层进行,能力强的用第一问的方法,自己探究,寻找题眼;有困难的根据提纲进行,老师适时指导。 首先,整体感知已知是什么: 1.两个正方形, 2.边长为4,3.旋转。其次, 明确做什么:重叠部分的面积S, (1)它变不变,为什么? (2)如不变 的话,怎样算。 规律:1、第一,三,五幅图重叠部分的面积都 等于正方形ABCD的四分之一; 2、第三,四,五幅图重叠部分的面积都被OB分成两个三角形,且 随着旋转,一个变大,另一个变小。 猜想:重叠部分的面积不变;等于正方形面积的四分之一。 分析探究:第一,二,三幅图的重叠部分,欲证S重=S△AOB, 而S△AOB=S1+S3, S重=S3+S2, 即证:S1+S3=S3+S2,所以需证S1=S2 结合图形,得出题眼: 证△AOM≌△BON。 二、探究问题: 1.仔细思考,看在旋转中,还有什么时候重叠部分的图形也比较特殊? 2..OB是∠ABC的什么线 该怎样作辅助线?作出看能解决吗? 找出题眼:证△MHO≌△NKO。 三、规律总结: 这类运动类问题以后你们该怎样入手? 一、题图结合,明确问题; 二、想象运动,分析规律; 三、作出猜想,找出题眼; 四、理顺关系,完成答题。 A 组同学直接按刚才的方法思考第2。 B 组的同学先独立思考,有问题的按下列提纲提示进行。 一、题图结合,明确问题;三角形NBM的周长(y=BM+BN+MN)变不变及范 围问题。 二、想象运动,分析规律; BM逐渐变小,BN逐渐变大,但,BM+BN=4 , 但MN由大逐渐到小,到最小又逐渐到大。 三、作出猜想,找出题眼; 因为 y=4+MN ,所以线段MN的取值范围就是题眼。 思考: (1) MN最长接近多少,能等于它吗? (2)MN有最小值,为多少? 当MN最小时,两种情况下M点在AB的位置一样吗? 四:拓展思维 已知:如图所示,两个正方形边长都为4,其中正方形OEFG以正方形ABCD的对角线交点O为中心进行旋转。 1. 求△MBN的最大面积。 2. 两个正方形的重叠部分的周长 会变 化吗?为什么? 3. 求DF的范围。 4. 当∠AOE=30°时,求AM的长。 六、课后作业 见作业纸
- 1 -
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
