人教版数学八年级下册 18.1.2 第3课时 三角形的中位线 课件 (共20张PPT)
文档属性
| 名称 | 人教版数学八年级下册 18.1.2 第3课时 三角形的中位线 课件 (共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 385.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-04 17:43:42 | ||
图片预览








文档简介
(共20张PPT)
第十八章 平行四边形
18.1.1 平行四边形的性质
第2课时 三角形的中位线
1.理解三角形中位线的概念,掌握它的性质.
2.能较熟练地应用三角形中位线性质进行有关的证明和计算.
3.能运用综合法证明有关三角形中位线性质的结论.理解在证明过程中所运用的归纳、类比、转化等思想方法.
重点难点:
1.理解三角形中位线的概念,掌握三角形的中位线定理.
2.能利用三角形的中位线定理解决有关证明和计算问题.
学习目标:
我们探索平行四边形时,常常转化为三角形,利用三角形的全等性质进行研究,今天我们一起来利用平行四边形来探索三角形的某些问题吧.
思考 如图,有一块三角形蛋糕,准备平分给四个小朋友,要求四人所分的形状大小相同,该怎样分呢?
情景导入
知识精讲
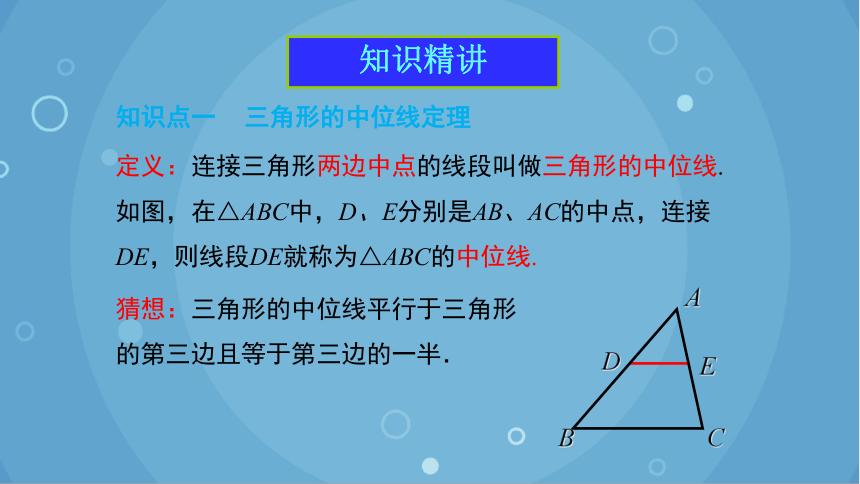
知识点一 三角形的中位线定理
定义:连接三角形两边中点的线段叫做三角形的中位线.
A
B
C
D
E
如图,在△ABC中,D、E分别是AB、AC的中点,连接DE,则线段DE就称为△ABC的中位线.
猜想:三角形的中位线平行于三角形的第三边且等于第三边的一半.
证明:延长DE到F,使EF=DE.
连接AF、CF、DC .
∵AE=EC,DE=EF ,
∴四边形ADCF是平行四边形.∴CF AD ,∴CF BD ,
∴四边形BCFD是平行四边形,∴DF BC .
又∵ ,∴ DE∥BC, .
D
E
F
如图,在△ABC中,点D,E分别是AB,AC边的中点,
求证:
D
E
证明:
延长DE到F,使EF=DE.
F
∴四边形BCFD是平行四边形.
∴△ADE≌△CFE.
∴∠ADE=∠F
连接FC.
∵∠AED=∠CEF,AE=CE,
证法2:
,AD=CF,
∴BD CF.
又∵ ,
∴DF BC .
∴ DE∥BC, .
∴CF AD ,
D
E
△ABC中,若D、E分别是边AB、AC的中点,
则DE∥BC,DE= BC.
归纳:三角形中位线定理是指三角形的中位线平行于三角形的第三边且等于第三边的一半.
符号语言:
例1 如图,在△ABC中,D、E分别为AC、BC的中点,AF平分∠CAB,交DE于点F.若DF=3,求AC的长
解:∵D、E分别为AC、BC的中点,
∴DE∥AB,∴∠2=∠3.
又∵AF平分∠CAB,
∴∠1=∠3,∴∠1=∠2,
∴AD=DF=3,
∴AC=2AD=2DF=6.
1
2
3
例2 如图,在△ABC中,AB=AC,E为AB的中点,在AB的延长线上取一点D,使BD=AB,求证:CD=2CE.
证明:取AC的中点F,连接BF.∵BD=AB,
∴BF为△ADC的中位线,∴DC=2BF.
∵E为AB的中点,AB=AC,
∴BE=CF,∠ABC=∠ACB.
∵BC=CB,∴△EBC≌△FCB,∴CE=BF,∴CD=2CE.
F
归纳:恰当地构造三角形中位线是解决线段倍分关系的关键.
针对练习
1. 如图,△ABC中,D、E分别是AB、AC中点.
(1) 若DE=5,则BC= .
(2) 若∠B=65°,则∠ADE= °.
(3) 若DE+BC=12,则BC= .
10
65
8
2.如图,A,B两点被池塘隔开,在A,B外选一点C,连接AC和BC,并分别找出AC和BC的中点M,N,如果测得MN=20m,那么A,B两点间的距离为______m.
N
M
40
知识点二 三角形的中位线与平行四边形的综合运用
例3 如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA中点.
求证:四边形EFGH是平行四边形.
证明:连接AC.
∵E,F,G,H分别为各边的中点,
∴ EF∥HG, EF=HG.
∴EF∥AC,
HG∥AC,
∴四边形EFGH是平行四边形.
针对练习
1.如图,在△ABC中,AB=6,AC=10,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为 ( )
A.8 B.10 C.12 D.16
D
2.如图, ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,求△DOE的周长.
解:∵ ABCD的周长为36,
∴BC+CD=18.
∵点E是CD的中点,
∴OE是△BCD的中位线,DE= CD,
∴OE= BC,
∴△DOE的周长为OD+OE+DE=
(BD+BC+CD)=15,
即△DOE的周长为15.
当堂检测
1.如图,在△ABC中,点E、F分别为AB、AC的中点.若EF的长为2,则BC的长为 ( )
A.1
B.2
C.4
D.8
C
2.如图,点 D、E、F 分别是 △ABC 的三边AB、BC、AC的中点.
(1)若∠ADF=50°,则∠B= °;
(2)已知三边AB、BC、AC分别为12、10、8,
则△ DEF的周长为 .
50
15
A
B
C
D
F
E
3.如图,在△ABC中,AB=6cm,AC=10cm,AD平分∠BAC,BD⊥AD于点D,BD的延长线交AC于 点F,E为BC的中点,求DE的长.
解:∵AD平分∠BAC,BD⊥AD,
∴AB=AF=6cm,BD=DF,
∴CF=AC-AF=4cm,
∵BD=DF,E为BC的中点,
∴DE= CF=2cm.
4.如图,E为 ABCD中DC边的延长线上一点,且CE=DC,连接AE,分别交BC、BD于点F、G,连接AC交BD于O,连接OF,判断AB与OF的位置关系和大小关系,并证明你的结论.
解:AB∥OF,AB=2OF.
证明如下:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OA=OC,
∴∠BAF=∠CEF,∠ABF=∠ECF.
∵CE=DC,∴AB=CE,
∴△ABF≌△ECF(ASA),
∴BF=CF.
∵OA=OC,
∴OF是△ABC的中位线,
∴AB∥OF,AB=2OF.
5.如图,在四边形ABCD中,AC⊥BD,BD=12,AC=16,E,F分别为AB,CD的中点,求EF的长.
解:取BC边的中点G,连接EG、FG.
∵E,F分别为AB,CD的中点,
∴EG是△ABC的中位线,FG是△BCD的中位线,
又BD=12,AC=16,AC⊥BD,
∴EG=8,FG=6,EG⊥FG,
∴
∴EG∥AC,
FG∥BD,
G
当堂检测
三角形的中位线
三角形中位线平行于第三边,并且等于它的一半
三角形的中位线定理
三角形的中位线定理的应用
第十八章 平行四边形
18.1.1 平行四边形的性质
第2课时 三角形的中位线
1.理解三角形中位线的概念,掌握它的性质.
2.能较熟练地应用三角形中位线性质进行有关的证明和计算.
3.能运用综合法证明有关三角形中位线性质的结论.理解在证明过程中所运用的归纳、类比、转化等思想方法.
重点难点:
1.理解三角形中位线的概念,掌握三角形的中位线定理.
2.能利用三角形的中位线定理解决有关证明和计算问题.
学习目标:
我们探索平行四边形时,常常转化为三角形,利用三角形的全等性质进行研究,今天我们一起来利用平行四边形来探索三角形的某些问题吧.
思考 如图,有一块三角形蛋糕,准备平分给四个小朋友,要求四人所分的形状大小相同,该怎样分呢?
情景导入
知识精讲
知识点一 三角形的中位线定理
定义:连接三角形两边中点的线段叫做三角形的中位线.
A
B
C
D
E
如图,在△ABC中,D、E分别是AB、AC的中点,连接DE,则线段DE就称为△ABC的中位线.
猜想:三角形的中位线平行于三角形的第三边且等于第三边的一半.
证明:延长DE到F,使EF=DE.
连接AF、CF、DC .
∵AE=EC,DE=EF ,
∴四边形ADCF是平行四边形.∴CF AD ,∴CF BD ,
∴四边形BCFD是平行四边形,∴DF BC .
又∵ ,∴ DE∥BC, .
D
E
F
如图,在△ABC中,点D,E分别是AB,AC边的中点,
求证:
D
E
证明:
延长DE到F,使EF=DE.
F
∴四边形BCFD是平行四边形.
∴△ADE≌△CFE.
∴∠ADE=∠F
连接FC.
∵∠AED=∠CEF,AE=CE,
证法2:
,AD=CF,
∴BD CF.
又∵ ,
∴DF BC .
∴ DE∥BC, .
∴CF AD ,
D
E
△ABC中,若D、E分别是边AB、AC的中点,
则DE∥BC,DE= BC.
归纳:三角形中位线定理是指三角形的中位线平行于三角形的第三边且等于第三边的一半.
符号语言:
例1 如图,在△ABC中,D、E分别为AC、BC的中点,AF平分∠CAB,交DE于点F.若DF=3,求AC的长
解:∵D、E分别为AC、BC的中点,
∴DE∥AB,∴∠2=∠3.
又∵AF平分∠CAB,
∴∠1=∠3,∴∠1=∠2,
∴AD=DF=3,
∴AC=2AD=2DF=6.
1
2
3
例2 如图,在△ABC中,AB=AC,E为AB的中点,在AB的延长线上取一点D,使BD=AB,求证:CD=2CE.
证明:取AC的中点F,连接BF.∵BD=AB,
∴BF为△ADC的中位线,∴DC=2BF.
∵E为AB的中点,AB=AC,
∴BE=CF,∠ABC=∠ACB.
∵BC=CB,∴△EBC≌△FCB,∴CE=BF,∴CD=2CE.
F
归纳:恰当地构造三角形中位线是解决线段倍分关系的关键.
针对练习
1. 如图,△ABC中,D、E分别是AB、AC中点.
(1) 若DE=5,则BC= .
(2) 若∠B=65°,则∠ADE= °.
(3) 若DE+BC=12,则BC= .
10
65
8
2.如图,A,B两点被池塘隔开,在A,B外选一点C,连接AC和BC,并分别找出AC和BC的中点M,N,如果测得MN=20m,那么A,B两点间的距离为______m.
N
M
40
知识点二 三角形的中位线与平行四边形的综合运用
例3 如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA中点.
求证:四边形EFGH是平行四边形.
证明:连接AC.
∵E,F,G,H分别为各边的中点,
∴ EF∥HG, EF=HG.
∴EF∥AC,
HG∥AC,
∴四边形EFGH是平行四边形.
针对练习
1.如图,在△ABC中,AB=6,AC=10,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为 ( )
A.8 B.10 C.12 D.16
D
2.如图, ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,求△DOE的周长.
解:∵ ABCD的周长为36,
∴BC+CD=18.
∵点E是CD的中点,
∴OE是△BCD的中位线,DE= CD,
∴OE= BC,
∴△DOE的周长为OD+OE+DE=
(BD+BC+CD)=15,
即△DOE的周长为15.
当堂检测
1.如图,在△ABC中,点E、F分别为AB、AC的中点.若EF的长为2,则BC的长为 ( )
A.1
B.2
C.4
D.8
C
2.如图,点 D、E、F 分别是 △ABC 的三边AB、BC、AC的中点.
(1)若∠ADF=50°,则∠B= °;
(2)已知三边AB、BC、AC分别为12、10、8,
则△ DEF的周长为 .
50
15
A
B
C
D
F
E
3.如图,在△ABC中,AB=6cm,AC=10cm,AD平分∠BAC,BD⊥AD于点D,BD的延长线交AC于 点F,E为BC的中点,求DE的长.
解:∵AD平分∠BAC,BD⊥AD,
∴AB=AF=6cm,BD=DF,
∴CF=AC-AF=4cm,
∵BD=DF,E为BC的中点,
∴DE= CF=2cm.
4.如图,E为 ABCD中DC边的延长线上一点,且CE=DC,连接AE,分别交BC、BD于点F、G,连接AC交BD于O,连接OF,判断AB与OF的位置关系和大小关系,并证明你的结论.
解:AB∥OF,AB=2OF.
证明如下:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OA=OC,
∴∠BAF=∠CEF,∠ABF=∠ECF.
∵CE=DC,∴AB=CE,
∴△ABF≌△ECF(ASA),
∴BF=CF.
∵OA=OC,
∴OF是△ABC的中位线,
∴AB∥OF,AB=2OF.
5.如图,在四边形ABCD中,AC⊥BD,BD=12,AC=16,E,F分别为AB,CD的中点,求EF的长.
解:取BC边的中点G,连接EG、FG.
∵E,F分别为AB,CD的中点,
∴EG是△ABC的中位线,FG是△BCD的中位线,
又BD=12,AC=16,AC⊥BD,
∴EG=8,FG=6,EG⊥FG,
∴
∴EG∥AC,
FG∥BD,
G
当堂检测
三角形的中位线
三角形中位线平行于第三边,并且等于它的一半
三角形的中位线定理
三角形的中位线定理的应用
