四年级数学下册课件-7三角形-平行四边形和梯形苏教版(共29张PPT)
文档属性
| 名称 | 四年级数学下册课件-7三角形-平行四边形和梯形苏教版(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 237.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-03 17:04:23 | ||
图片预览



文档简介
(共29张PPT)
苏教版四年级第七单元
三角形、平行四边形和梯形
复习驿站
容错展板
典型例题分析
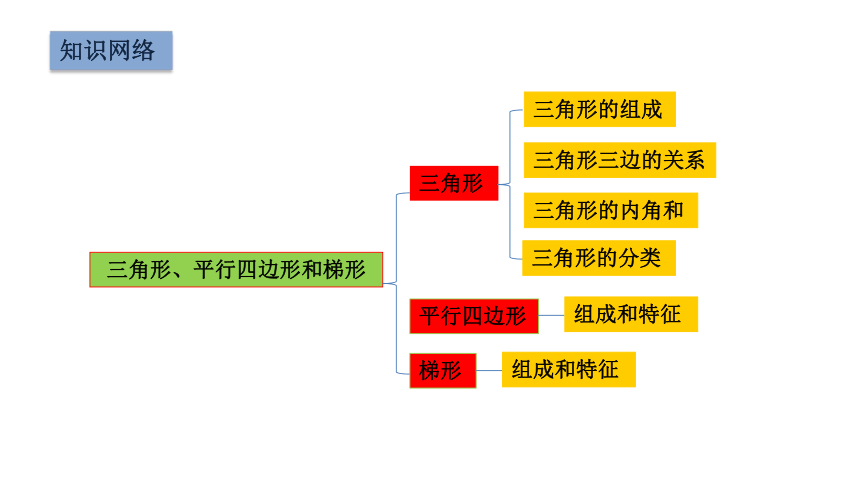
知识网络
知识网络
三角形、平行四边形和梯形
三角形
平行四边形
梯形
三角形的组成
三角形三边的关系
三角形的内角和
三角形的分类
组成和特征
组成和特征
复习驿站
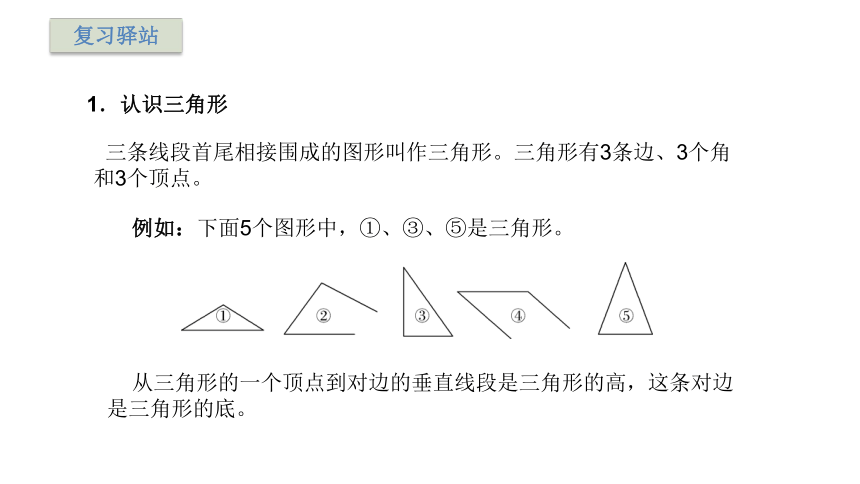
1.认识三角形
三条线段首尾相接围成的图形叫作三角形。三角形有3条边、3个角和3个顶点。
例如:下面5个图形中,①、③、⑤是三角形。
从三角形的一个顶点到对边的垂直线段是三角形的高,这条对边是三角形的底。
复习驿站
2.三角形三边之间的关系
三角形任意两边长度的和大于第三边。
3.三角形的内角和
三角形的内角和等于180°。已知三角形中一个角或两个角的度数,要求剩下角的度数,可以用180°减去已知角的度数。
复习驿站
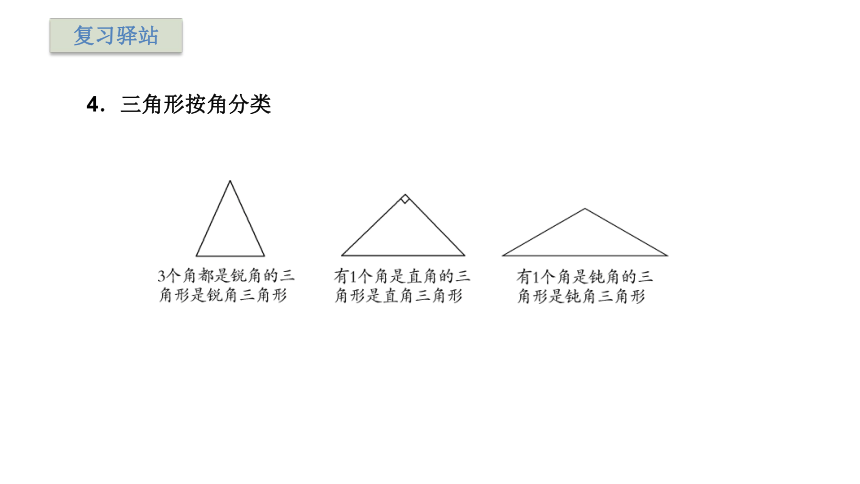
4.三角形按角分类
复习驿站
5.特殊的三角形
两条边相等的三角形是等腰三角形。等腰三角形的两个底角相等,它是轴对称图形,有一条对称轴,等腰三角形底边上的高在它的对称轴上。三条边相等的三角形是等边三角形,又叫正三角形。等边三角形的三个角都相等,都是60°,它也是轴对称图形,并且有三条对称轴,等边三角形的三条高都在它的对称轴上。
复习驿站
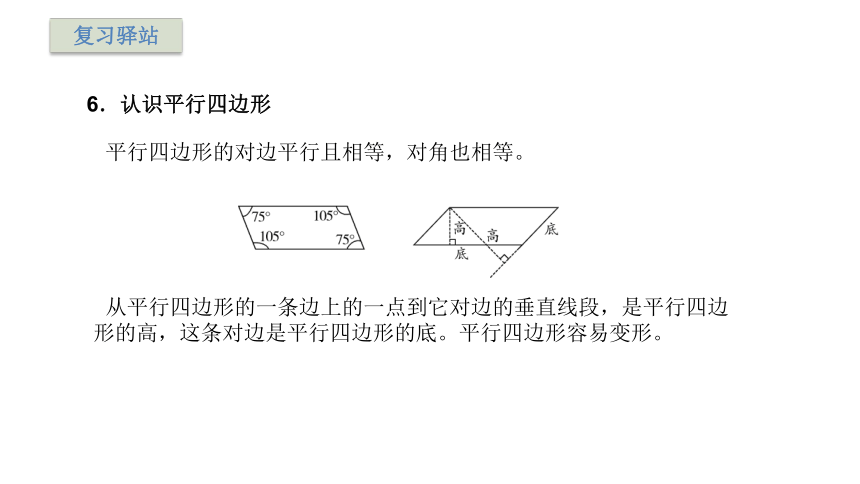
6.认识平行四边形
平行四边形的对边平行且相等,对角也相等。
从平行四边形的一条边上的一点到它对边的垂直线段,是平行四边形的高,这条对边是平行四边形的底。平行四边形容易变形。
复习驿站
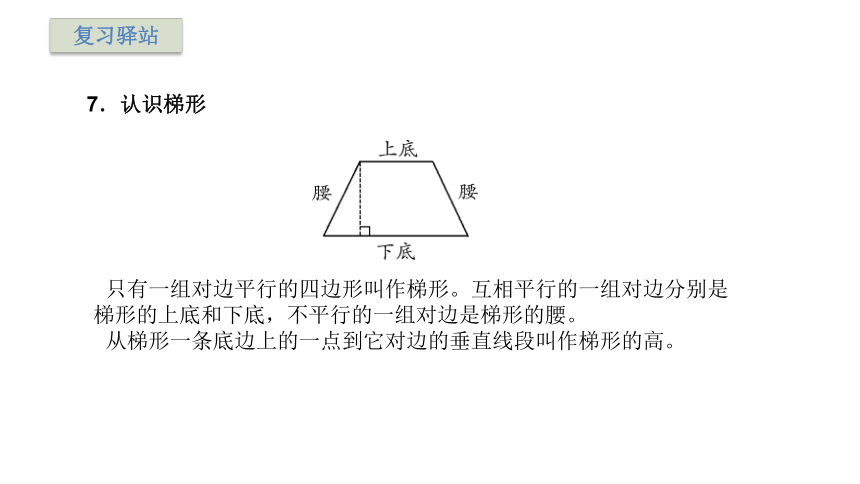
7.认识梯形
只有一组对边平行的四边形叫作梯形。互相平行的一组对边分别是梯形的上底和下底,不平行的一组对边是梯形的腰。
从梯形一条底边上的一点到它对边的垂直线段叫作梯形的高。
典型例题分析
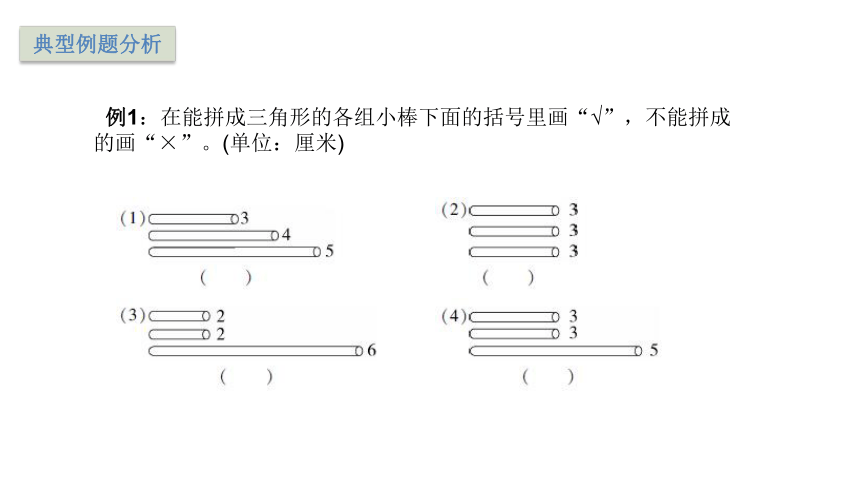
例1:在能拼成三角形的各组小棒下面的括号里画“√”,不能拼成的画“×”。(单位:厘米)
典型例题分析
分析:三角形任意两边之和大于第三边”,而在实际应用中,要判断三根小棒是否可以拼成三角形,只要将其中较短的两边之和与第三边进行比较就行了。如果较短的两边之和大于第三边,那么这三根小棒就一定能拼成三角形;如果较短的两边之和小于或等于第三边,那么这三根小棒就一定不能拼成三角形。
(1)因为3+4>5,所以这三根小棒能拼成三角形;
(2)因为3+3>3,所以这三根小棒能拼成三角形;
(3)因为2+2<6,所以这三根小棒不能拼成三角形;
(4)因为3+3>5,所以这三根小棒能拼成三角形。
典型例题分析
解答:(1)√ (2)√ (3)× (4)√
典型例题分析
例2:下图中已知∠1=120°,∠4=40°,求∠3的度数。
典型例题分析
分析:要求出∠3的度数,只要知道∠2的度数就可以了。而∠2+∠1=180°,∠1=120°,所以可以求出∠2=180°-120°=60°,然后再根据三角形的内角和是180°,用180°-∠2-∠4就能求出∠3的度数。
典型例题分析
解答:∠2=180°-120°=60°
∠3=180°-∠2-∠4
=180°-40°-60°
=80°
答:∠3的度数为80°。
典型例题分析
例3:选择:在一个三角形中,两个内角度数的和小于第三个内角,这个三角形是( )三角形。
A.锐角 B.直角 C.钝角
典型例题分析
分析:三角形的三个内角的和等于180°,如果其中两个内角之和小于第三个内角,说明第三个内角大于90°,根据将三角形按角分类的标准,可作出正确选择。
典型例题分析
解答:C
典型例题分析
例4:一个梯形的下底是上底的3倍,如果将上底延长6厘米,就成了一个平行四边形,这个梯形的下底是多少厘米?
典型例题分析
分析:由题意可知梯形的下底比上底多2倍,又因为平行四边形对边相等,所以这个“2倍“的长度就是6厘米,所以梯形的上底的长度就是6÷2=3(厘米)。据此可求出梯形的下底长度是多少。
典型例题分析
解答:6÷(3-1)=3(厘米) 3×3=9(厘米)
答:这个梯形的下底是9厘米。
典型例题分析
例5:求下面两个图形的内角和。
典型例题分析
分析:这两个图形分别是四边形和五边形。可以选择一个顶点(如下图),把它与不相邻的顶点连接起来,这样四边形就分成了2个三角形,五边形就分成了3个三角形。仔细观察就会发现,四边形的四个内角的和就是把它分成的2个三角形的所有内角的和,也就是一个三角形内角和的2倍;五边形的内角和就是把它分成的3个三角形的所有内角的和,也就是一个三角形内角和的3倍。
典型例题分析
解答:180°×2=360° 180°×3=540°
答:四边形的内角和是360°,五边形的内角和是540°。
容错展板
错例1. 判断:等腰三角形一定是锐角三角形。(√)
错解分析:等边三角形三条边相等,三个角也相等,每一个角都是60°,而等腰三角形只是两条边相等,与角的大小无关,所以等腰三角形可能是锐角三角形,可能是直角三角形,也可能是钝角三角形。
容错展板
正确解答:×
(对应训练参见学生用书第十三周复习第二题第3小题内容)
容错展板
容错展板
错例2. 平行四边形的高有( B )条。
A.1 B.2 C.无数
错解分析:认为平行四边形的高只有2条。三角形中一个顶点只可以向对边作1条高,所以三角形只有3条高,但是平行四边形一条边上有无数个点可以向对边作无数条高,所以平行四边形有无数条高。
容错展板
正确解答:C
(对应训练参见学生用书第十四周复习第一题第4小题内容)
容错展板
苏教版四年级第七单元
三角形、平行四边形和梯形
复习驿站
容错展板
典型例题分析
知识网络
知识网络
三角形、平行四边形和梯形
三角形
平行四边形
梯形
三角形的组成
三角形三边的关系
三角形的内角和
三角形的分类
组成和特征
组成和特征
复习驿站
1.认识三角形
三条线段首尾相接围成的图形叫作三角形。三角形有3条边、3个角和3个顶点。
例如:下面5个图形中,①、③、⑤是三角形。
从三角形的一个顶点到对边的垂直线段是三角形的高,这条对边是三角形的底。
复习驿站
2.三角形三边之间的关系
三角形任意两边长度的和大于第三边。
3.三角形的内角和
三角形的内角和等于180°。已知三角形中一个角或两个角的度数,要求剩下角的度数,可以用180°减去已知角的度数。
复习驿站
4.三角形按角分类
复习驿站
5.特殊的三角形
两条边相等的三角形是等腰三角形。等腰三角形的两个底角相等,它是轴对称图形,有一条对称轴,等腰三角形底边上的高在它的对称轴上。三条边相等的三角形是等边三角形,又叫正三角形。等边三角形的三个角都相等,都是60°,它也是轴对称图形,并且有三条对称轴,等边三角形的三条高都在它的对称轴上。
复习驿站
6.认识平行四边形
平行四边形的对边平行且相等,对角也相等。
从平行四边形的一条边上的一点到它对边的垂直线段,是平行四边形的高,这条对边是平行四边形的底。平行四边形容易变形。
复习驿站
7.认识梯形
只有一组对边平行的四边形叫作梯形。互相平行的一组对边分别是梯形的上底和下底,不平行的一组对边是梯形的腰。
从梯形一条底边上的一点到它对边的垂直线段叫作梯形的高。
典型例题分析
例1:在能拼成三角形的各组小棒下面的括号里画“√”,不能拼成的画“×”。(单位:厘米)
典型例题分析
分析:三角形任意两边之和大于第三边”,而在实际应用中,要判断三根小棒是否可以拼成三角形,只要将其中较短的两边之和与第三边进行比较就行了。如果较短的两边之和大于第三边,那么这三根小棒就一定能拼成三角形;如果较短的两边之和小于或等于第三边,那么这三根小棒就一定不能拼成三角形。
(1)因为3+4>5,所以这三根小棒能拼成三角形;
(2)因为3+3>3,所以这三根小棒能拼成三角形;
(3)因为2+2<6,所以这三根小棒不能拼成三角形;
(4)因为3+3>5,所以这三根小棒能拼成三角形。
典型例题分析
解答:(1)√ (2)√ (3)× (4)√
典型例题分析
例2:下图中已知∠1=120°,∠4=40°,求∠3的度数。
典型例题分析
分析:要求出∠3的度数,只要知道∠2的度数就可以了。而∠2+∠1=180°,∠1=120°,所以可以求出∠2=180°-120°=60°,然后再根据三角形的内角和是180°,用180°-∠2-∠4就能求出∠3的度数。
典型例题分析
解答:∠2=180°-120°=60°
∠3=180°-∠2-∠4
=180°-40°-60°
=80°
答:∠3的度数为80°。
典型例题分析
例3:选择:在一个三角形中,两个内角度数的和小于第三个内角,这个三角形是( )三角形。
A.锐角 B.直角 C.钝角
典型例题分析
分析:三角形的三个内角的和等于180°,如果其中两个内角之和小于第三个内角,说明第三个内角大于90°,根据将三角形按角分类的标准,可作出正确选择。
典型例题分析
解答:C
典型例题分析
例4:一个梯形的下底是上底的3倍,如果将上底延长6厘米,就成了一个平行四边形,这个梯形的下底是多少厘米?
典型例题分析
分析:由题意可知梯形的下底比上底多2倍,又因为平行四边形对边相等,所以这个“2倍“的长度就是6厘米,所以梯形的上底的长度就是6÷2=3(厘米)。据此可求出梯形的下底长度是多少。
典型例题分析
解答:6÷(3-1)=3(厘米) 3×3=9(厘米)
答:这个梯形的下底是9厘米。
典型例题分析
例5:求下面两个图形的内角和。
典型例题分析
分析:这两个图形分别是四边形和五边形。可以选择一个顶点(如下图),把它与不相邻的顶点连接起来,这样四边形就分成了2个三角形,五边形就分成了3个三角形。仔细观察就会发现,四边形的四个内角的和就是把它分成的2个三角形的所有内角的和,也就是一个三角形内角和的2倍;五边形的内角和就是把它分成的3个三角形的所有内角的和,也就是一个三角形内角和的3倍。
典型例题分析
解答:180°×2=360° 180°×3=540°
答:四边形的内角和是360°,五边形的内角和是540°。
容错展板
错例1. 判断:等腰三角形一定是锐角三角形。(√)
错解分析:等边三角形三条边相等,三个角也相等,每一个角都是60°,而等腰三角形只是两条边相等,与角的大小无关,所以等腰三角形可能是锐角三角形,可能是直角三角形,也可能是钝角三角形。
容错展板
正确解答:×
(对应训练参见学生用书第十三周复习第二题第3小题内容)
容错展板
容错展板
错例2. 平行四边形的高有( B )条。
A.1 B.2 C.无数
错解分析:认为平行四边形的高只有2条。三角形中一个顶点只可以向对边作1条高,所以三角形只有3条高,但是平行四边形一条边上有无数个点可以向对边作无数条高,所以平行四边形有无数条高。
容错展板
正确解答:C
(对应训练参见学生用书第十四周复习第一题第4小题内容)
容错展板
