北师大版数学七年级下册 2.3 平行线性质与判定的综合运用(第1课时)课件 (共20张PPT)
文档属性
| 名称 | 北师大版数学七年级下册 2.3 平行线性质与判定的综合运用(第1课时)课件 (共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 333.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-04 20:19:41 | ||
图片预览


文档简介
(共21张PPT)
第二章 相交线与平行线
专题课堂 探索平行线的判定和性质综合应用的规律
三角尺在平行线中的应用
【例1】 (遵义中考)已知a∥b,某学生将一直角三角板放置如图所示,如果∠1=35°,求∠2的度数.
解:∵a∥b,
∴∠3=∠4,
∵∠3=∠1,
∴∠1=∠4,
∵∠5+∠4=90°,且∠5=∠2,
∴∠1+∠2=90°,
∵∠1=35°,
∴∠2=55°
1.(自贡中考)在平面内,将一个直角三角板按如图所示摆放在一组平行线上;若∠1=55°,则∠2的度数是( )
A.50° B.45° C.40° D.35°
D
2.(枣庄中考)已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=20°,则∠2的度数为( )
A.20° B.30° C.45° D.50°
D
3.(随州中考)如图,在平行线l1,l2之间放置一块直角三角板,三角板的锐角顶点A,B分别在直线l1,l2上,若∠1=65°,则∠2的度数是( )
A.25° B.35° C.45° D.65°
A
【例2】 (聊城中考)如图,直线AB∥EF,点C是直线AB上一点,点D是直线AB外一点,若∠BCD=95°,∠CDE=25°,求∠DEF的度数.
解:过点D作DM∥EF,
∵直线AB∥EF,∴DM∥EF∥AB,∴∠BCD+∠CDM=180°,∴∠CDM=85°,
∵∠CDE=25°,∴MDE=85°-25°=60°,
∵∠DEF +∠EDM=180°,
∴∠DEF=120°
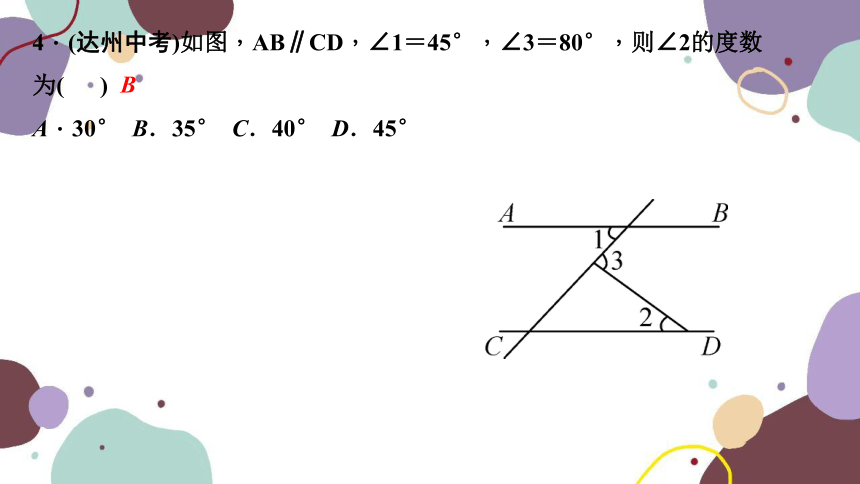
4.(达州中考)如图,AB∥CD,∠1=45°,∠3=80°,则∠2的度数为( )
A.30° B.35° C.40° D.45°
B
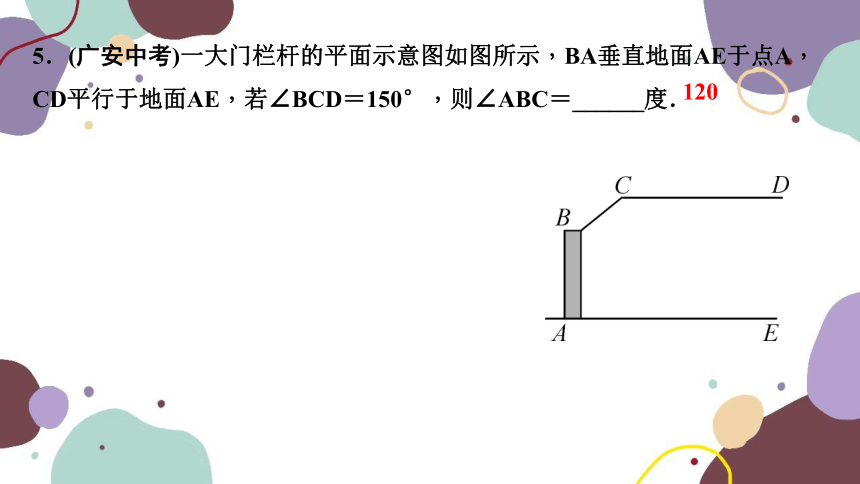
5.(广安中考)一大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=150°,则∠ABC=______度.
120
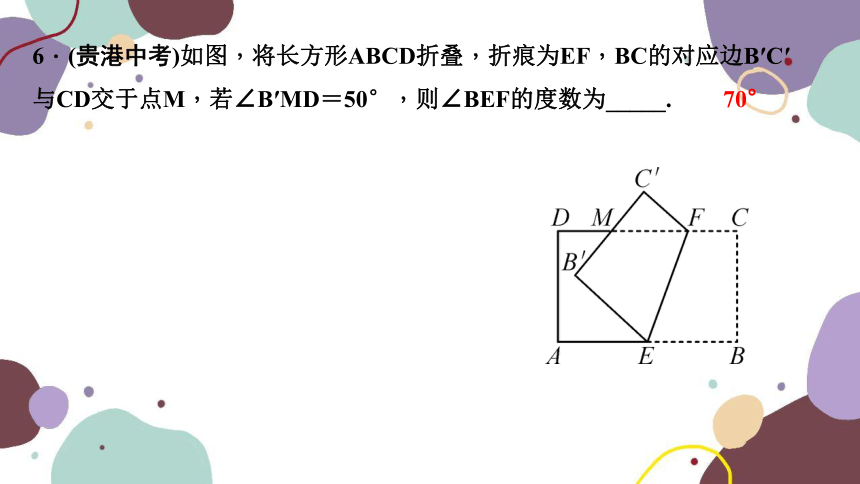
6.(贵港中考)如图,将长方形ABCD折叠,折痕为EF,BC的对应边B′C′与CD交于点M,若∠B′MD=50°,则∠BEF的度数为_____.
70°
探究平行线之间角的关系
【例3】 如图,若AB∥CD,在下列三种情况下探究∠APC与∠PAB,∠PCD的数量关系.
(1)在图①中,∠APC+∠PAB+∠PCD=________;
(2)在图②中,∠PAB+∠PCD=________;
(3)在图③中,写出∠APC与∠PAB,∠PCD三者的数量关系,并说明理由.
解:(1)360°
(2)∠APC
(3)∠PCD=∠PAB+∠APC.理由:过点P作PE∥AB(E在直线PC右侧),∴∠PAB+(∠APC+∠CPE)=180°.又∵AB∥CD,∴PE∥CD,∴∠CPE+∠PCD=180°,∴∠PAB+∠APC+∠CPE=∠CPE+∠PCD,∴∠PAB+∠APC=∠PCD,即∠PCD=∠PAB+∠APC
7.如图,已知AB∥CD,BC∥DE.若∠A=20°,∠C=120°,则∠AED的度数是________.
80°
8.如图,已知AM∥BN,∠A=52°,点P是射线AM上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由,若变化,请写出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
(2)不变化,∠APB=2∠ADB,证明:∵AM∥BN,∴∠APB=∠PBN,∠ADB=∠DBN,又∵BD平分∠PBN,∴∠PBN=2∠DBN,∴∠APB=2∠ADB
平行线的判定、性质的推理证明
【例4】 如图,CD⊥AB于点D,点F是BC上任意一点,FE⊥AB于点E,且∠1=∠2,∠3=80°.
(1)试说明∠B=∠ADG;
(2)求∠BCA的度数.
解:(1)∵CD⊥AB,EF⊥AB,
∴CD∥EF,
∴∠2=∠DCF,
∵∠1=∠2,
∴∠1=∠DCF,
∴DG∥BC,
∴∠B=∠ADG
(2)由(1)得DG∥BC,
∴∠BCA=∠3=80°
9.如果∠α与∠β的两边分别平行,∠α比∠β的三倍少24°,则∠α的度数是_____________.
12或129度
10.如图,AB与CD交于点O,OE平分∠AOC,点F为AB上一点(不与点A及O重合),过点F作FG∥OE,交CD于点G,若∠AOD=110°,则∠AFG度数为____________.
35°或145°
11.如图,AD平分∠BAC,AD⊥BC于点D,E,A,C三点共线,∠DAC=∠EFA,延长EF交BC于点G.
(1)求证:EG⊥BC;
(2)若将AD平分∠BAC与EG⊥BC互换,其他条件不变,结论是否仍然成立?说明理由.
解:(1)∵AD平分∠BAC, ∴∠1=∠2,
∵∠2=∠EFA, ∴∠1=∠EFA,∴AD∥EG,
∵AD⊥BC,∴EG⊥BC
(2)结论仍然成立.理由:∵AD⊥BC,EG⊥BC,
∴AD∥EG,
∴∠1=∠EFA,
∵∠2=∠EFA,
∴∠1=∠2,
∴AD平分∠BAC
第二章 相交线与平行线
专题课堂 探索平行线的判定和性质综合应用的规律
三角尺在平行线中的应用
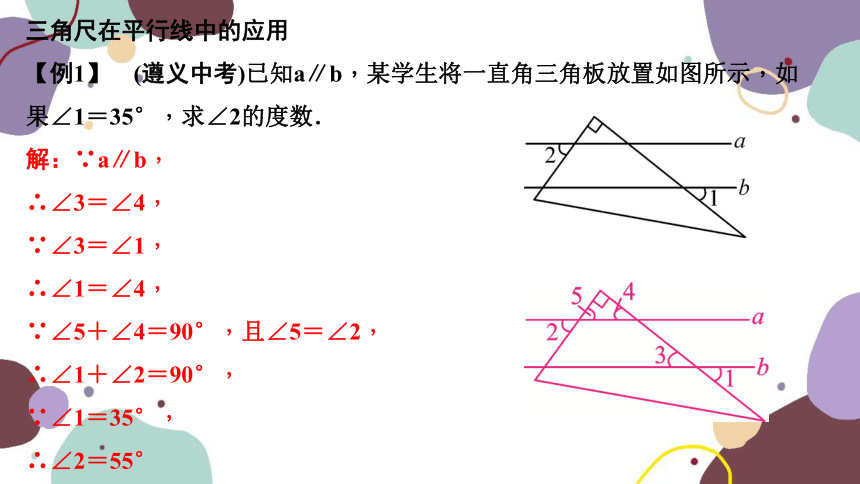
【例1】 (遵义中考)已知a∥b,某学生将一直角三角板放置如图所示,如果∠1=35°,求∠2的度数.
解:∵a∥b,
∴∠3=∠4,
∵∠3=∠1,
∴∠1=∠4,
∵∠5+∠4=90°,且∠5=∠2,
∴∠1+∠2=90°,
∵∠1=35°,
∴∠2=55°
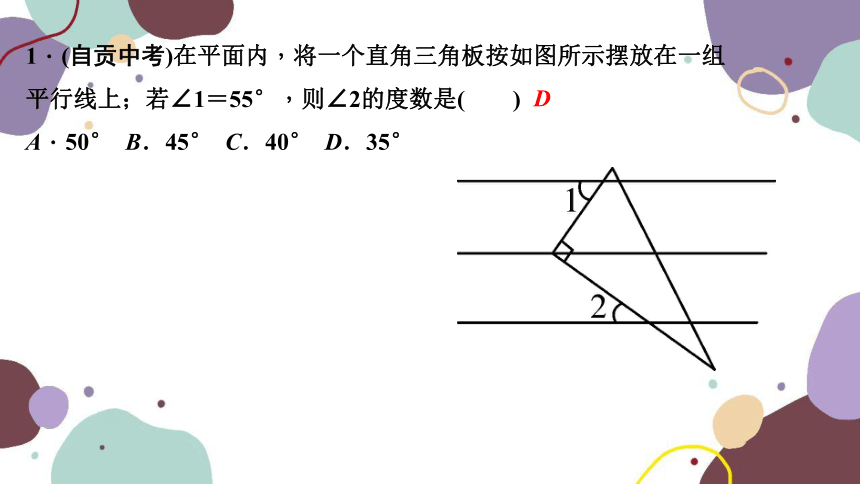
1.(自贡中考)在平面内,将一个直角三角板按如图所示摆放在一组平行线上;若∠1=55°,则∠2的度数是( )
A.50° B.45° C.40° D.35°
D
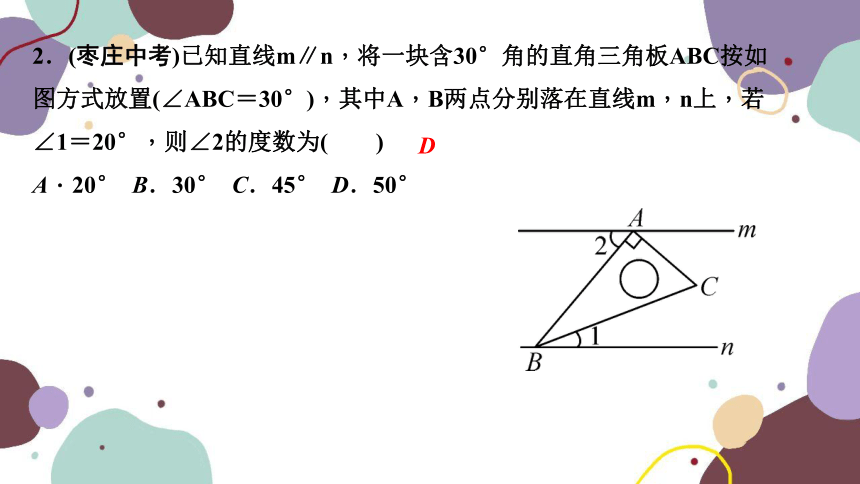
2.(枣庄中考)已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=20°,则∠2的度数为( )
A.20° B.30° C.45° D.50°
D
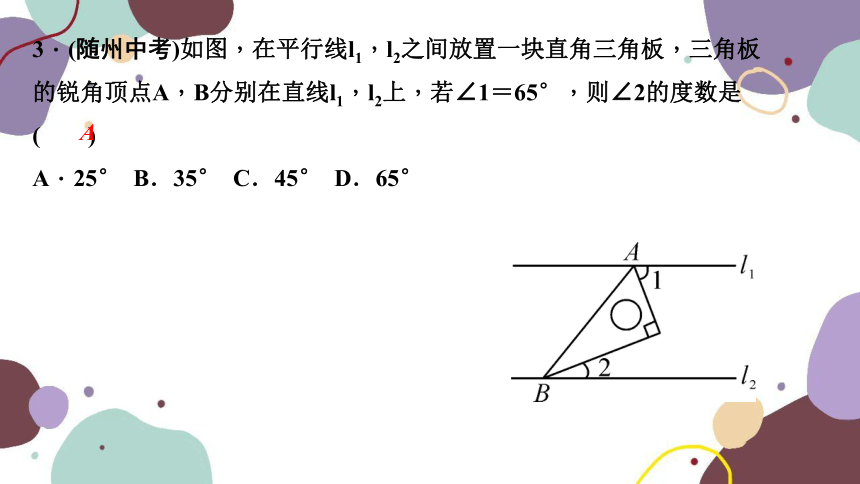
3.(随州中考)如图,在平行线l1,l2之间放置一块直角三角板,三角板的锐角顶点A,B分别在直线l1,l2上,若∠1=65°,则∠2的度数是( )
A.25° B.35° C.45° D.65°
A
【例2】 (聊城中考)如图,直线AB∥EF,点C是直线AB上一点,点D是直线AB外一点,若∠BCD=95°,∠CDE=25°,求∠DEF的度数.
解:过点D作DM∥EF,
∵直线AB∥EF,∴DM∥EF∥AB,∴∠BCD+∠CDM=180°,∴∠CDM=85°,
∵∠CDE=25°,∴MDE=85°-25°=60°,
∵∠DEF +∠EDM=180°,
∴∠DEF=120°
4.(达州中考)如图,AB∥CD,∠1=45°,∠3=80°,则∠2的度数为( )
A.30° B.35° C.40° D.45°
B
5.(广安中考)一大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=150°,则∠ABC=______度.
120
6.(贵港中考)如图,将长方形ABCD折叠,折痕为EF,BC的对应边B′C′与CD交于点M,若∠B′MD=50°,则∠BEF的度数为_____.
70°
探究平行线之间角的关系
【例3】 如图,若AB∥CD,在下列三种情况下探究∠APC与∠PAB,∠PCD的数量关系.
(1)在图①中,∠APC+∠PAB+∠PCD=________;
(2)在图②中,∠PAB+∠PCD=________;
(3)在图③中,写出∠APC与∠PAB,∠PCD三者的数量关系,并说明理由.
解:(1)360°
(2)∠APC
(3)∠PCD=∠PAB+∠APC.理由:过点P作PE∥AB(E在直线PC右侧),∴∠PAB+(∠APC+∠CPE)=180°.又∵AB∥CD,∴PE∥CD,∴∠CPE+∠PCD=180°,∴∠PAB+∠APC+∠CPE=∠CPE+∠PCD,∴∠PAB+∠APC=∠PCD,即∠PCD=∠PAB+∠APC
7.如图,已知AB∥CD,BC∥DE.若∠A=20°,∠C=120°,则∠AED的度数是________.
80°
8.如图,已知AM∥BN,∠A=52°,点P是射线AM上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由,若变化,请写出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
(2)不变化,∠APB=2∠ADB,证明:∵AM∥BN,∴∠APB=∠PBN,∠ADB=∠DBN,又∵BD平分∠PBN,∴∠PBN=2∠DBN,∴∠APB=2∠ADB
平行线的判定、性质的推理证明
【例4】 如图,CD⊥AB于点D,点F是BC上任意一点,FE⊥AB于点E,且∠1=∠2,∠3=80°.
(1)试说明∠B=∠ADG;
(2)求∠BCA的度数.
解:(1)∵CD⊥AB,EF⊥AB,
∴CD∥EF,
∴∠2=∠DCF,
∵∠1=∠2,
∴∠1=∠DCF,
∴DG∥BC,
∴∠B=∠ADG
(2)由(1)得DG∥BC,
∴∠BCA=∠3=80°
9.如果∠α与∠β的两边分别平行,∠α比∠β的三倍少24°,则∠α的度数是_____________.
12或129度
10.如图,AB与CD交于点O,OE平分∠AOC,点F为AB上一点(不与点A及O重合),过点F作FG∥OE,交CD于点G,若∠AOD=110°,则∠AFG度数为____________.
35°或145°
11.如图,AD平分∠BAC,AD⊥BC于点D,E,A,C三点共线,∠DAC=∠EFA,延长EF交BC于点G.
(1)求证:EG⊥BC;
(2)若将AD平分∠BAC与EG⊥BC互换,其他条件不变,结论是否仍然成立?说明理由.
解:(1)∵AD平分∠BAC, ∴∠1=∠2,
∵∠2=∠EFA, ∴∠1=∠EFA,∴AD∥EG,
∵AD⊥BC,∴EG⊥BC
(2)结论仍然成立.理由:∵AD⊥BC,EG⊥BC,
∴AD∥EG,
∴∠1=∠EFA,
∵∠2=∠EFA,
∴∠1=∠2,
∴AD平分∠BAC
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
