2022届高考物理冲刺专题第1期—热学模型 学案(word版无答案)
文档属性
| 名称 | 2022届高考物理冲刺专题第1期—热学模型 学案(word版无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 511.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-03 14:48:40 | ||
图片预览




文档简介
热学模型——高考必得15分专题
一、“玻璃管液封”模型
1.三大气体实验定律
(1)玻意耳定律(等温变化):p1V1=p2V2或pV=C(常数)。
(2)查理定律(等容变化):或=C(常数)。
(3)盖—吕萨克定律(等压变化):或=C(常数)。
2.利用气体实验定律及气态方程解决问题的基本思路
3.玻璃管液封模型
求液柱封闭的气体压强时,一般以液柱为研究对象分析受力、列平衡方程,要注意:
(1)液体因重力产生的压强大小为p=ρgh(其中h为至液面的竖直高度);
(2)不要漏掉大气压强;
(3)有时可直接应用连通器原理——连通器内静止的液体,同种液体在同一水平面上各处压强相等;
(4)当液体为水银时,可灵活应用压强单位“cmHg”等,使计算过程简捷。
【模型演练1】(2020·全国卷Ⅲ)
1.如图,两侧粗细均匀、横截面积相等、高度均为H=18cm的U型管,左管上端封闭,右管上端开口。右管中有高h0= 4cm的水银柱,水银柱上表面离管口的距离l= 12cm。管底水平段的体积可忽略。环境温度为T1=283K。大气压强p0=76cmHg。
(1)现从右侧端口缓慢注入水银(与原水银柱之间无气隙),恰好使水银柱下端到达右管底部。此时水银柱的高度为多少?(保留一位小数)
(2)再将左管中密封气体缓慢加热,使水银柱上表面恰与右管口平齐,此时密封气体的温度为多少?
【模型演练2】(2021·广东广州市、深圳市学调联盟高三第二次调研)
2.如图,粗细均匀的弯曲玻璃管A、B两端开口,管内有一段水银柱,中管内水银面与管口A之间气体柱长为lA=40 cm,右管内气体柱长为lB=39 cm.先将开口B封闭,再将左管竖直插入水银槽中,设被封闭的气体为理想气体,整个过程温度不变,若稳定后进入左管的水银面比水银槽水银面低4 cm,已知大气压强p0=76 cmHg,求:
(1)A端上方气柱长度;
(2)稳定后右管内的气体压强.
【模型演练3】(2021·贵州六盘水市·高三一模)
3.如图,一端封闭且粗细均匀的细玻璃管中,用长10 cm的水银柱封闭了一段空气,当玻璃管与水平面夹角为30°倾斜放置时水银柱上端恰好与管口相齐,空气柱长17 cm。已知大气压强为75 cm Hg,保持环境温度27℃不变,缓慢旋转玻璃管至开口竖直向上。
(1)求玻璃管开口向上竖直放置时被封空气柱的长度;
(2)保持玻璃管开口向上竖直放置,缓慢加热空气柱使水银面与管口齐平,求此时空气柱的温度。(保留整数)
二、“汽缸活塞类”模型
汽缸活塞类问题是热学部分典型的物理综合题,它需要考虑气体、汽缸或活塞等多个研究对象,涉及热学、力学等物理知识,需要灵活、综合地应用知识来解决问题。
1.一般思路
(1)确定研究对象,一般地说,研究对象分两类:一类是热学研究对象(一定质量的理想气体);另一类是力学研究对象(汽缸、活塞或某系统)。
(2)分析物理过程,对热学研究对象分析清楚初、末状态及状态变化过程,依据气体实验定律列出方程;对力学研究对象要正确地进行受力分析,依据力学规律列出方程。
(3)挖掘题目的隐含条件,如几何关系等,列出辅助方程。
(4)多个方程联立求解。对求解的结果注意检验它们的合理性。
2.常见类型
(1)气体系统处于平衡状态,需综合应用气体实验定律和物体的平衡条件解题。
(2)气体系统处于力学非平衡状态,需要综合应用气体实验定律和牛顿运动定律解题。
(3)两个或多个汽缸封闭着几部分气体,并且汽缸之间相互关联的问题,解答时应分别研究各部分气体,找出它们各自遵循的规律,并写出相应的方程,还要写出各部分气体之间压强或体积的关系式,最后联立求解。
【模型演练4】(2021·“八省联考”辽宁省普通高中学业水平选择考适应性测试)
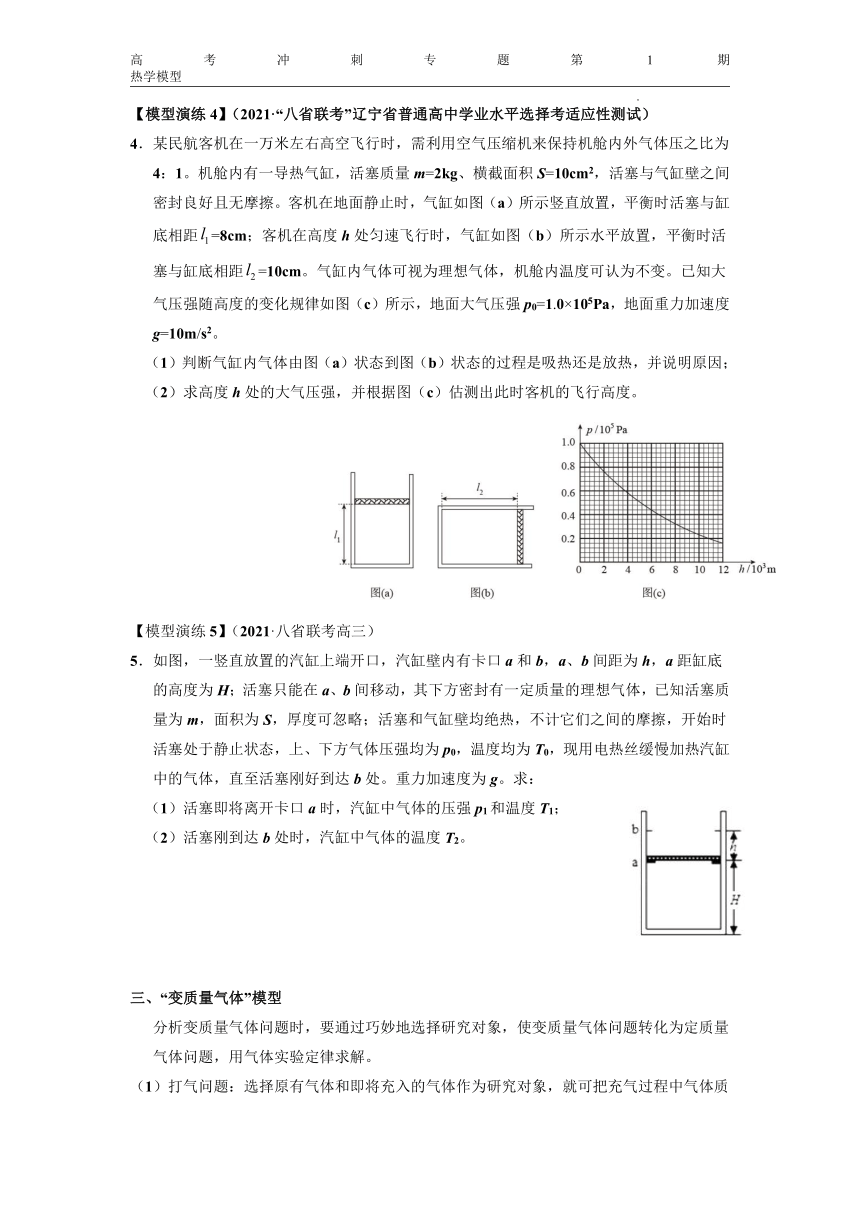
4.某民航客机在一万米左右高空飞行时,需利用空气压缩机来保持机舱内外气体压之比为4:1。机舱内有一导热气缸,活塞质量m=2kg、横截面积S=10cm2,活塞与气缸壁之间密封良好且无摩擦。客机在地面静止时,气缸如图(a)所示竖直放置,平衡时活塞与缸底相距=8cm;客机在高度h处匀速飞行时,气缸如图(b)所示水平放置,平衡时活塞与缸底相距=10cm。气缸内气体可视为理想气体,机舱内温度可认为不变。已知大气压强随高度的变化规律如图(c)所示,地面大气压强p0=1.0×105Pa,地面重力加速度g=10m/s2。
(1)判断气缸内气体由图(a)状态到图(b)状态的过程是吸热还是放热,并说明原因;
(2)求高度h处的大气压强,并根据图(c)估测出此时客机的飞行高度。
【模型演练5】(2021·八省联考高三)
5.如图,一竖直放置的汽缸上端开口,汽缸壁内有卡口a和b,a、b间距为h,a距缸底的高度为H;活塞只能在a、b间移动,其下方密封有一定质量的理想气体,已知活塞质量为m,面积为S,厚度可忽略;活塞和气缸壁均绝热,不计它们之间的摩擦,开始时活塞处于静止状态,上、下方气体压强均为p0,温度均为T0,现用电热丝缓慢加热汽缸中的气体,直至活塞刚好到达b处。重力加速度为g。求:
(1)活塞即将离开卡口a时,汽缸中气体的压强p1和温度T1;
(2)活塞刚到达b处时,汽缸中气体的温度T2。
三、“变质量气体”模型
分析变质量气体问题时,要通过巧妙地选择研究对象,使变质量气体问题转化为定质量气体问题,用气体实验定律求解。
(1)打气问题:选择原有气体和即将充入的气体作为研究对象,就可把充气过程中气体质量变化问题转化为定质量气体的状态变化问题。
(2)抽气问题:将每次抽气过程中抽出的气体和剩余气体作为研究对象,质量不变,故抽气过程可以看成是等温膨胀过程。
(3)灌气问题:把大容器中的剩余气体和多个小容器中的气体整体作为研究对象,可将变质量问题转化为定质量问题。
(4)漏气问题:选容器内剩余气体和漏出气体整体作为研究对象,便可使问题变成一定质量气体的状态变化,可用理想气体的状态方程求解。
【模型演练6】
6.新冠肺炎疫情发生以来,各医院都特别加强了内部环境消毒工作。如图所示,是某医院消毒喷雾器设备。喷雾器的储液桶与打气筒用软细管相连,已知储液桶容积为10L,打气筒每打次气能向储液桶内压入Pa的空气。现往储液桶内装入8L药液后关紧桶盖和喷雾头开关,此时桶内压强为Pa,打气过程中储液桶内气体温度与外界温度相同且保持不变,不计储液桶两端连接管以及软细管的容积。
(1)若打气使储液桶内消毒液上方的气体压强达到3×105Pa后,求打气筒打气次数至少是多少?
(2)当储液桶内消毒液上方的气体压强达到3×105Pa后,打开喷雾器开关K直至储液桶消毒液上方的气压为2×105Pa,求在这过程中储液桶喷出药液的体积是多少?
【模型演练7】(2021·重庆市九龙坡区一模)
7.如图所示,水平放置粗细均匀的玻璃管,管口用橡胶塞封住,一可自由移动的活塞将玻璃管内分隔为A、B两部分,两部分中均有理想气体。开始时活塞静止,A部分气体的体积是B部分气体体积的2.5倍,其压强均为p。现松动橡胶塞,使B中气体向外缓慢漏出,整个过程中气体温度保持不变。当A部分气体的体积变为原来的1.2倍时,再将橡胶塞塞紧,求B中剩余气体与漏气前B中气体的质量比。(不计活塞与管壁间的摩擦)
【模型演练8】(2021·山东省昌乐第一中学高三期末)
8.如图所示,气缸中有一可自由滑动的活塞把气缸隔成两个密闭的气室,左室顶部有一个截面积为的圆孔,初始时两个气室与外界大气相通,体积均为。圆孔中塞上质量为的橡皮塞,橡皮塞与圆孔间的最大静摩擦力为,用打气筒向右侧气室打气,直至橡皮塞刚好上滑。气体温度均保持不变,室外空气密度为,大气压强为,重力加速度为,求:
(1)橡皮塞刚好上滑时左室气体的体积;
(2)为了使橡皮塞刚好上滑,需要向右侧气室内打入的空气质量。
三年高考乙卷(I卷)真题练习
1.(2021·高考)如图,一定量的理想气体从状态经热力学过程、、后又回到状态a。对于、、三个过程,下列说法正确的是( )
A.过程中,气体始终吸热
B.过程中,气体始终放热
C.过程中,气体对外界做功
D.过程中,气体的温度先降低后升高
E.过程中,气体的温度先升高后降低
2.(2021·高考)如图,一玻璃装置放在水平桌面上,竖直玻璃管A、B、C粗细均匀,A、B两管的上端封闭,C管上端开口,三管的下端在同一水平面内且相互连通。A、B两管的长度分别为,。将水银从C管缓慢注入,直至B、C两管内水银柱的高度差。已知外界大气压为。求A、B两管内水银柱的高度差。
3.(2020·高考)分子间作用力F与分子间距r的关系如图所示,r= r1时,F=0。分子间势能由r决定,规定两分子相距无穷远时分子间的势能为零。若一分子固定于原点O,另一分子从距O点很远处向O点运动,在两分子间距减小到r2的过程中,势能_____(填“减小“不变”或“增大”);在间距由r2减小到r1的过程中,势能_____ (填“减小”“不变”或“增大”);在间距等于r1处,势能_____(填“大于”“等于”或“小于”)零。
4.(2020·高考)甲、乙两个储气罐储存有同种气体(可视为理想气体)。甲罐的容积为V,罐中气体的压强为p;乙罐的容积为2V,罐中气体的压强为。现通过连接两罐的细管把甲罐中的部分气体调配到乙罐中去,两罐中气体温度相同且在调配过程中保持不变,调配后两罐中气体的压强相等。求调配后:
(1)两罐中气体的压强;
(2)甲罐中气体的质量与甲罐中原有气体的质量之比。
5.(2019·高考)某容器中的空气被光滑活塞封住,容器和活塞绝热性能良好,空气可视为理想气体.初始时容器中空气的温度与外界相同,压强大于外界.现使活塞缓慢移动,直至容器中的空气压强与外界相同.此时,容器中空气的温度__________(填“高于”“低于”或“等于”)外界温度,容器中空气的密度__________(填“大于”“小于”或“等于”)外界空气的密度。
6.(2019·高考)热等静压设备广泛用于材料加工中.该设备工作时,先在室温下把惰性气体用压缩机压入到一个预抽真空的炉腔中,然后炉腔升温,利用高温高气压环境对放入炉腔中的材料加工处理,改部其性能.一台热等静压设备的炉腔中某次放入固体材料后剩余的容积为0.13 m3,炉腔抽真空后,在室温下用压缩机将10瓶氩气压入到炉腔中.已知每瓶氩气的容积为3.2×10-2 m3,使用前瓶中气体压强为1.5×107 Pa,使用后瓶中剩余气体压强为2.0×106 Pa;室温温度为27 ℃.氩气可视为理想气体.
(1)求压入氩气后炉腔中气体在室温下的压强;
(2)将压入氩气后的炉腔加热到1 227 ℃,求此时炉腔中气体的压强.
高考冲刺专题第1期 热学模型
一、“玻璃管液封”模型
1.三大气体实验定律
(1)玻意耳定律(等温变化):p1V1=p2V2或pV=C(常数)。
(2)查理定律(等容变化):或=C(常数)。
(3)盖—吕萨克定律(等压变化):或=C(常数)。
2.利用气体实验定律及气态方程解决问题的基本思路
3.玻璃管液封模型
求液柱封闭的气体压强时,一般以液柱为研究对象分析受力、列平衡方程,要注意:
(1)液体因重力产生的压强大小为p=ρgh(其中h为至液面的竖直高度);
(2)不要漏掉大气压强;
(3)有时可直接应用连通器原理——连通器内静止的液体,同种液体在同一水平面上各处压强相等;
(4)当液体为水银时,可灵活应用压强单位“cmHg”等,使计算过程简捷。
【模型演练1】(2020·全国卷Ⅲ)
1.如图,两侧粗细均匀、横截面积相等、高度均为H=18cm的U型管,左管上端封闭,右管上端开口。右管中有高h0= 4cm的水银柱,水银柱上表面离管口的距离l= 12cm。管底水平段的体积可忽略。环境温度为T1=283K。大气压强p0=76cmHg。
(1)现从右侧端口缓慢注入水银(与原水银柱之间无气隙),恰好使水银柱下端到达右管底部。此时水银柱的高度为多少?(保留一位小数)
(2)再将左管中密封气体缓慢加热,使水银柱上表面恰与右管口平齐,此时密封气体的温度为多少?
【模型演练2】(2021·广东广州市、深圳市学调联盟高三第二次调研)
2.如图,粗细均匀的弯曲玻璃管A、B两端开口,管内有一段水银柱,中管内水银面与管口A之间气体柱长为lA=40 cm,右管内气体柱长为lB=39 cm.先将开口B封闭,再将左管竖直插入水银槽中,设被封闭的气体为理想气体,整个过程温度不变,若稳定后进入左管的水银面比水银槽水银面低4 cm,已知大气压强p0=76 cmHg,求:
(1)A端上方气柱长度;
(2)稳定后右管内的气体压强.
【模型演练3】(2021·贵州六盘水市·高三一模)
3.如图,一端封闭且粗细均匀的细玻璃管中,用长10 cm的水银柱封闭了一段空气,当玻璃管与水平面夹角为30°倾斜放置时水银柱上端恰好与管口相齐,空气柱长17 cm。已知大气压强为75 cm Hg,保持环境温度27℃不变,缓慢旋转玻璃管至开口竖直向上。
(1)求玻璃管开口向上竖直放置时被封空气柱的长度;
(2)保持玻璃管开口向上竖直放置,缓慢加热空气柱使水银面与管口齐平,求此时空气柱的温度。(保留整数)
二、“汽缸活塞类”模型
汽缸活塞类问题是热学部分典型的物理综合题,它需要考虑气体、汽缸或活塞等多个研究对象,涉及热学、力学等物理知识,需要灵活、综合地应用知识来解决问题。
1.一般思路
(1)确定研究对象,一般地说,研究对象分两类:一类是热学研究对象(一定质量的理想气体);另一类是力学研究对象(汽缸、活塞或某系统)。
(2)分析物理过程,对热学研究对象分析清楚初、末状态及状态变化过程,依据气体实验定律列出方程;对力学研究对象要正确地进行受力分析,依据力学规律列出方程。
(3)挖掘题目的隐含条件,如几何关系等,列出辅助方程。
(4)多个方程联立求解。对求解的结果注意检验它们的合理性。
2.常见类型
(1)气体系统处于平衡状态,需综合应用气体实验定律和物体的平衡条件解题。
(2)气体系统处于力学非平衡状态,需要综合应用气体实验定律和牛顿运动定律解题。
(3)两个或多个汽缸封闭着几部分气体,并且汽缸之间相互关联的问题,解答时应分别研究各部分气体,找出它们各自遵循的规律,并写出相应的方程,还要写出各部分气体之间压强或体积的关系式,最后联立求解。
【模型演练4】(2021·“八省联考”辽宁省普通高中学业水平选择考适应性测试)
4.某民航客机在一万米左右高空飞行时,需利用空气压缩机来保持机舱内外气体压之比为4:1。机舱内有一导热气缸,活塞质量m=2kg、横截面积S=10cm2,活塞与气缸壁之间密封良好且无摩擦。客机在地面静止时,气缸如图(a)所示竖直放置,平衡时活塞与缸底相距=8cm;客机在高度h处匀速飞行时,气缸如图(b)所示水平放置,平衡时活塞与缸底相距=10cm。气缸内气体可视为理想气体,机舱内温度可认为不变。已知大气压强随高度的变化规律如图(c)所示,地面大气压强p0=1.0×105Pa,地面重力加速度g=10m/s2。
(1)判断气缸内气体由图(a)状态到图(b)状态的过程是吸热还是放热,并说明原因;
(2)求高度h处的大气压强,并根据图(c)估测出此时客机的飞行高度。
【模型演练5】(2021·八省联考高三)
5.如图,一竖直放置的汽缸上端开口,汽缸壁内有卡口a和b,a、b间距为h,a距缸底的高度为H;活塞只能在a、b间移动,其下方密封有一定质量的理想气体,已知活塞质量为m,面积为S,厚度可忽略;活塞和气缸壁均绝热,不计它们之间的摩擦,开始时活塞处于静止状态,上、下方气体压强均为p0,温度均为T0,现用电热丝缓慢加热汽缸中的气体,直至活塞刚好到达b处。重力加速度为g。求:
(1)活塞即将离开卡口a时,汽缸中气体的压强p1和温度T1;
(2)活塞刚到达b处时,汽缸中气体的温度T2。
三、“变质量气体”模型
分析变质量气体问题时,要通过巧妙地选择研究对象,使变质量气体问题转化为定质量气体问题,用气体实验定律求解。
(1)打气问题:选择原有气体和即将充入的气体作为研究对象,就可把充气过程中气体质量变化问题转化为定质量气体的状态变化问题。
(2)抽气问题:将每次抽气过程中抽出的气体和剩余气体作为研究对象,质量不变,故抽气过程可以看成是等温膨胀过程。
(3)灌气问题:把大容器中的剩余气体和多个小容器中的气体整体作为研究对象,可将变质量问题转化为定质量问题。
(4)漏气问题:选容器内剩余气体和漏出气体整体作为研究对象,便可使问题变成一定质量气体的状态变化,可用理想气体的状态方程求解。
【模型演练6】
6.新冠肺炎疫情发生以来,各医院都特别加强了内部环境消毒工作。如图所示,是某医院消毒喷雾器设备。喷雾器的储液桶与打气筒用软细管相连,已知储液桶容积为10L,打气筒每打次气能向储液桶内压入Pa的空气。现往储液桶内装入8L药液后关紧桶盖和喷雾头开关,此时桶内压强为Pa,打气过程中储液桶内气体温度与外界温度相同且保持不变,不计储液桶两端连接管以及软细管的容积。
(1)若打气使储液桶内消毒液上方的气体压强达到3×105Pa后,求打气筒打气次数至少是多少?
(2)当储液桶内消毒液上方的气体压强达到3×105Pa后,打开喷雾器开关K直至储液桶消毒液上方的气压为2×105Pa,求在这过程中储液桶喷出药液的体积是多少?
【模型演练7】(2021·重庆市九龙坡区一模)
7.如图所示,水平放置粗细均匀的玻璃管,管口用橡胶塞封住,一可自由移动的活塞将玻璃管内分隔为A、B两部分,两部分中均有理想气体。开始时活塞静止,A部分气体的体积是B部分气体体积的2.5倍,其压强均为p。现松动橡胶塞,使B中气体向外缓慢漏出,整个过程中气体温度保持不变。当A部分气体的体积变为原来的1.2倍时,再将橡胶塞塞紧,求B中剩余气体与漏气前B中气体的质量比。(不计活塞与管壁间的摩擦)
【模型演练8】(2021·山东省昌乐第一中学高三期末)
8.如图所示,气缸中有一可自由滑动的活塞把气缸隔成两个密闭的气室,左室顶部有一个截面积为的圆孔,初始时两个气室与外界大气相通,体积均为。圆孔中塞上质量为的橡皮塞,橡皮塞与圆孔间的最大静摩擦力为,用打气筒向右侧气室打气,直至橡皮塞刚好上滑。气体温度均保持不变,室外空气密度为,大气压强为,重力加速度为,求:
(1)橡皮塞刚好上滑时左室气体的体积;
(2)为了使橡皮塞刚好上滑,需要向右侧气室内打入的空气质量。
三年高考乙卷(I卷)真题练习
1.(2021·高考)如图,一定量的理想气体从状态经热力学过程、、后又回到状态a。对于、、三个过程,下列说法正确的是( )
A.过程中,气体始终吸热
B.过程中,气体始终放热
C.过程中,气体对外界做功
D.过程中,气体的温度先降低后升高
E.过程中,气体的温度先升高后降低
2.(2021·高考)如图,一玻璃装置放在水平桌面上,竖直玻璃管A、B、C粗细均匀,A、B两管的上端封闭,C管上端开口,三管的下端在同一水平面内且相互连通。A、B两管的长度分别为,。将水银从C管缓慢注入,直至B、C两管内水银柱的高度差。已知外界大气压为。求A、B两管内水银柱的高度差。
3.(2020·高考)分子间作用力F与分子间距r的关系如图所示,r= r1时,F=0。分子间势能由r决定,规定两分子相距无穷远时分子间的势能为零。若一分子固定于原点O,另一分子从距O点很远处向O点运动,在两分子间距减小到r2的过程中,势能_____(填“减小“不变”或“增大”);在间距由r2减小到r1的过程中,势能_____ (填“减小”“不变”或“增大”);在间距等于r1处,势能_____(填“大于”“等于”或“小于”)零。
4.(2020·高考)甲、乙两个储气罐储存有同种气体(可视为理想气体)。甲罐的容积为V,罐中气体的压强为p;乙罐的容积为2V,罐中气体的压强为。现通过连接两罐的细管把甲罐中的部分气体调配到乙罐中去,两罐中气体温度相同且在调配过程中保持不变,调配后两罐中气体的压强相等。求调配后:
(1)两罐中气体的压强;
(2)甲罐中气体的质量与甲罐中原有气体的质量之比。
5.(2019·高考)某容器中的空气被光滑活塞封住,容器和活塞绝热性能良好,空气可视为理想气体.初始时容器中空气的温度与外界相同,压强大于外界.现使活塞缓慢移动,直至容器中的空气压强与外界相同.此时,容器中空气的温度__________(填“高于”“低于”或“等于”)外界温度,容器中空气的密度__________(填“大于”“小于”或“等于”)外界空气的密度。
6.(2019·高考)热等静压设备广泛用于材料加工中.该设备工作时,先在室温下把惰性气体用压缩机压入到一个预抽真空的炉腔中,然后炉腔升温,利用高温高气压环境对放入炉腔中的材料加工处理,改部其性能.一台热等静压设备的炉腔中某次放入固体材料后剩余的容积为0.13 m3,炉腔抽真空后,在室温下用压缩机将10瓶氩气压入到炉腔中.已知每瓶氩气的容积为3.2×10-2 m3,使用前瓶中气体压强为1.5×107 Pa,使用后瓶中剩余气体压强为2.0×106 Pa;室温温度为27 ℃.氩气可视为理想气体.
(1)求压入氩气后炉腔中气体在室温下的压强;
(2)将压入氩气后的炉腔加热到1 227 ℃,求此时炉腔中气体的压强.
高考冲刺专题第1期 热学模型
同课章节目录
