苏科版数学八下 8.3频率与概率 课件(共27张PPT)
文档属性
| 名称 | 苏科版数学八下 8.3频率与概率 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 753.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-05 07:18:52 | ||
图片预览








文档简介
(共27张PPT)
8.3 频率与概率(1)
一个随机事件发生的可能性有大有小
飞机失事会给旅客造成意外伤害.一家保险公司要为购买机票的旅客进行保险,应该向旅客收取多少保费呢?为此,保险公司必须计算飞机失事的可能性有多大。
概率
1. 随机事件发生的可能性有大有小. 一个事件发生的可能性大小的数值,称为这个事件发生的概率.
2. 如果用字母A 表示一个事件,那么P(A)表示事件A 发生的概率.
概率
3. 通常规定,必然事件A 发生的概率是1,记作P(A)=1;不可能事件A 发生的概率是0,记作P(A)=0;随机事件A 发生的概率P(A)是0 和1 之间的一个数, 记作0 < P(A)< 1.
如图,表示三种事件发生的概率:
根据概率的概念表示几种事件的概率
【例1】写出下列事件发生的概率的范围或取值:
(1)记“太阳从东方升起”为事件A,则P(A)=______;
(2)记“明天会下雨”为事件B,则P(B)的取值范围为_________;
(3)记“地球绕着月亮转”为事件C,则P(C)=______.
1
0 < P(B)< 1
0
根据概率的概念表示几种事件的概率
【变式1】“14人中至少有2人在同一个月过生日”这一事件发生的概率为P,则( )
A.P=0 B.0<P<1 C.P=1 D.P>1
C
【变式2】下列事件中,概率P=0的事件是( )
A.某地10月16日刮西北风
B.当x是有理数时,x2≥0
C.手电筒的电池没电,灯泡发亮
D.一个电影院某天的上座率超过45%
C
概率意义的理解
【例2】气象台预报“本市明天降水概率是90%”.对此信息,下列说法正确的是( )
A. 本市明天将有90% 的地区降水
B. 本市明天将有90% 的时间降水
C. 明天肯定下雨
D. 明天降水的可能性比较大
D
对于一个随机事件,它发生的概率是由它自身决定的,并且是客观存在的,概率是随机事件自身的属性.
概率反映了随机事件发生的可能性大小。
我们用什么方法才能知道一个随机事件发生的概率呢
频率估计概率
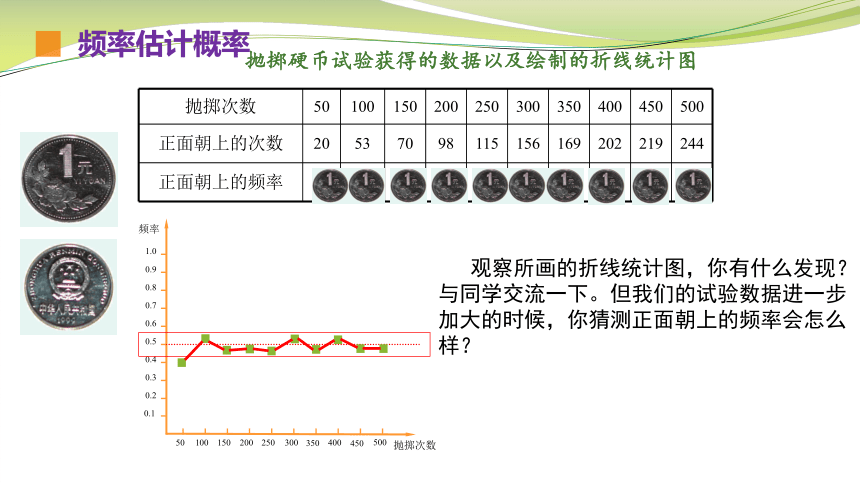
抛掷硬币试验获得的数据以及绘制的折线统计图
抛掷次数 50 100 150 200 250 300 350 400 450 500
正面朝上的次数 20 53 70 98 115 156 169 202 219 244
正面朝上的频率 0.4 0.53 0.47 0.49 0.46 0.52 0.48 0.51 0.49 0.49
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
50
100
150
200
250
300
350
400
450
500
频率
抛掷次数
观察所画的折线统计图,你有什么发现?与同学交流一下。但我们的试验数据进一步加大的时候,你猜测正面朝上的频率会怎么样?
频率估计概率
下表是自18世纪以来一些统计学家进行抛硬币试验所得的数据.
通过上表可以看出,当试验次数很大时,“正面朝上”的频率在______附近摆动。则与我们估计硬币正面朝上的概率____吻合
0.5
0.5
材料1:
通常,在多次重复试验中,一个随机事件发生的频率会在一个常数附近摆动,并且随着试验次数增多,摆动的幅度会减小,这个性质称为频率的稳定性.
频率估计概率
频率的定义
(2)注意:一般地,用频率估计概率时,试验次数应该尽可能多,试验次数越多,结果越接近事件发生的概率.
(3)概率是通过大量重复试验中频率的稳定性得到的介于0~1 的常数,它反映了事件发生的可能性大小.
概率意义的理解
当试验很多次时,平均每抛4次出现1次
“两个正面”
【变式1】
概率意义的理解
【变式2】下列说法正确的是( )
A. “明天降雨的概率为60%”表示明天有60%的时间都在下雨
B. “抛一枚硬币正面朝上的概率为50%”表示每抛2此就有一次正面朝上
C. “彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D. “抛一枚正方体骰子,朝上的点数为2的概率为1/6”表示随着抛掷次数的增加,“抛出朝上的点数为2的频率稳定在1/6”附近
D
利用频率估算概率
【例3】某射击运动员在同一条件下的射击成绩记录如下:
射击次数 20 80 100 200 400 1 000
“射中九环以上”的次数 18 68 82 168 327 823
“射中九环以上”的频率(结果保留两位小数) 0.90 0.85 0.82 0.84 0.82 0.82
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是( )
A.0.90 B.0.82
C.0.85 D.0.84
B
利用频率估算概率
【变式1】林业部门要考察某种幼树在一定条件下的移植成活率,如图是这种幼树在移植过程中幼树成活率的统计图:
估计该种幼树在此条件下移植成活的概率为________
(结果精确到0.01).
0.88
利用频率估算概率
【变式2】关于频率和概率的关系,下列说法正确的是( )
A. 频率等于概率
B. 当试验次数很大时,频率稳定在概率附近
C. 当试验次数很大时,概率稳定在频率附近
D. 试验得到的频率与概率不可能相同
B
根据频率的稳定性计算
【例4】在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小明通过多次试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球的个数最有可能是( )
A.5 B.10
C.12 D.15
A
根据频率的稳定性计算
【变式】在一个不透明的袋子中有10个除颜色外均相同的小球,通过多次摸球试验后,发现摸到白球的频率稳定在30%,估计袋子中白球有________个.
3
根据频率估算面积
【例5】一个圆形转盘的半径为2 cm,现将转盘分成若干个扇形,并分别相间涂上红、黄两种颜色.转盘转动10 000次,指针指向红色部分有2 500次.估计指针指向红色部分的概率是_______,转盘上黄色部分的面积约是_______.
0.25
3π cm2
根据频率估算面积
【变式】如图1所示,平整的地面上有一个不规则图案(图中阴影部分),小明想了解该图案的面积是多少,他采取了以下办法:用一个长为8m,宽为5m的长方形,将不规则图案围起来,然后在适当位置随机朝长方形区域扔小球,并记录小球落在不规则图案上的次数(小球扔在界线上或长方形区域外不计入试验结果),他将若干次有效试验的结果绘制成了图2所示的折线统计图,由此可估计不规则图案的面积大约是 .
14cm2
根据频率的稳定性设计方案
【例6】小红和小明在操场做游戏,他们先在地上画了半径分别2m和3m的同心圆(如图),蒙上眼在一定距离外向圈内掷小石子,掷中阴影小红胜,否则小明胜,未掷入圈内不算,你来当裁判.你认为游戏公平吗?为什么?
解:不公平,理由:
根据几何概率的求法:掷中阴影小红胜的概率就是阴影区域的面积与总面积的比值;小明胜的概率为小圆面积与总面积的比值,
而计算可得大圆面积为9π,小圆面积为4π.则阴影部分面积为5π,
则阴影部分面积比小圆面积大.
则小红胜的概率大于小明胜的概率,
所以该游戏是不公平的,对小红有利;
根据频率的稳定性设计方案
【变式】在一个不透明的口袋里装有颜色不同的黄、白两种颜色的球共5只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复…下表是活动中的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近______;(精确到0.1)
0.6
根据频率的稳定性设计方案
【变式】在一个不透明的口袋里装有颜色不同的黄、白两种颜色的球共5只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复…下表是活动中的一组统计数据:
(2)试估算口袋中白种颜色的球有多少只?
由(1)摸到白球的概率为0.6,所以可估计口袋中白种颜色的球的个数=5×0.6=3(只);
根据频率的稳定性设计方案
【变式】在一个不透明的口袋里装有颜色不同的黄、白两种颜色的球共5只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复…下表是活动中的一组统计数据:
(3)请你设计一个增(减)袋中白球或黄球球个数的方案,使得从袋中摸出一个球,这只球是黄球的概率大于是白球的概率.
由于现有白球3只,黄球2只,故要使黄球的概率大于是白球的概率,则增加2个以上黄球或减少2个以上白球.
课堂小结
频率与概率
概率
频率与概率的关系
不可能事件A发生的概率是0
随机事件A发生的概率是0和1之间的一个数
必然事件A发生的概率是1
利用频率估计等可能事件的概率
利用频率估计非等可能事件的概率
谢谢收看!
8.3 频率与概率(1)
一个随机事件发生的可能性有大有小
飞机失事会给旅客造成意外伤害.一家保险公司要为购买机票的旅客进行保险,应该向旅客收取多少保费呢?为此,保险公司必须计算飞机失事的可能性有多大。
概率
1. 随机事件发生的可能性有大有小. 一个事件发生的可能性大小的数值,称为这个事件发生的概率.
2. 如果用字母A 表示一个事件,那么P(A)表示事件A 发生的概率.
概率
3. 通常规定,必然事件A 发生的概率是1,记作P(A)=1;不可能事件A 发生的概率是0,记作P(A)=0;随机事件A 发生的概率P(A)是0 和1 之间的一个数, 记作0 < P(A)< 1.
如图,表示三种事件发生的概率:
根据概率的概念表示几种事件的概率
【例1】写出下列事件发生的概率的范围或取值:
(1)记“太阳从东方升起”为事件A,则P(A)=______;
(2)记“明天会下雨”为事件B,则P(B)的取值范围为_________;
(3)记“地球绕着月亮转”为事件C,则P(C)=______.
1
0 < P(B)< 1
0
根据概率的概念表示几种事件的概率
【变式1】“14人中至少有2人在同一个月过生日”这一事件发生的概率为P,则( )
A.P=0 B.0<P<1 C.P=1 D.P>1
C
【变式2】下列事件中,概率P=0的事件是( )
A.某地10月16日刮西北风
B.当x是有理数时,x2≥0
C.手电筒的电池没电,灯泡发亮
D.一个电影院某天的上座率超过45%
C
概率意义的理解
【例2】气象台预报“本市明天降水概率是90%”.对此信息,下列说法正确的是( )
A. 本市明天将有90% 的地区降水
B. 本市明天将有90% 的时间降水
C. 明天肯定下雨
D. 明天降水的可能性比较大
D
对于一个随机事件,它发生的概率是由它自身决定的,并且是客观存在的,概率是随机事件自身的属性.
概率反映了随机事件发生的可能性大小。
我们用什么方法才能知道一个随机事件发生的概率呢
频率估计概率
抛掷硬币试验获得的数据以及绘制的折线统计图
抛掷次数 50 100 150 200 250 300 350 400 450 500
正面朝上的次数 20 53 70 98 115 156 169 202 219 244
正面朝上的频率 0.4 0.53 0.47 0.49 0.46 0.52 0.48 0.51 0.49 0.49
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
50
100
150
200
250
300
350
400
450
500
频率
抛掷次数
观察所画的折线统计图,你有什么发现?与同学交流一下。但我们的试验数据进一步加大的时候,你猜测正面朝上的频率会怎么样?
频率估计概率
下表是自18世纪以来一些统计学家进行抛硬币试验所得的数据.
通过上表可以看出,当试验次数很大时,“正面朝上”的频率在______附近摆动。则与我们估计硬币正面朝上的概率____吻合
0.5
0.5
材料1:
通常,在多次重复试验中,一个随机事件发生的频率会在一个常数附近摆动,并且随着试验次数增多,摆动的幅度会减小,这个性质称为频率的稳定性.
频率估计概率
频率的定义
(2)注意:一般地,用频率估计概率时,试验次数应该尽可能多,试验次数越多,结果越接近事件发生的概率.
(3)概率是通过大量重复试验中频率的稳定性得到的介于0~1 的常数,它反映了事件发生的可能性大小.
概率意义的理解
当试验很多次时,平均每抛4次出现1次
“两个正面”
【变式1】
概率意义的理解
【变式2】下列说法正确的是( )
A. “明天降雨的概率为60%”表示明天有60%的时间都在下雨
B. “抛一枚硬币正面朝上的概率为50%”表示每抛2此就有一次正面朝上
C. “彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D. “抛一枚正方体骰子,朝上的点数为2的概率为1/6”表示随着抛掷次数的增加,“抛出朝上的点数为2的频率稳定在1/6”附近
D
利用频率估算概率
【例3】某射击运动员在同一条件下的射击成绩记录如下:
射击次数 20 80 100 200 400 1 000
“射中九环以上”的次数 18 68 82 168 327 823
“射中九环以上”的频率(结果保留两位小数) 0.90 0.85 0.82 0.84 0.82 0.82
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是( )
A.0.90 B.0.82
C.0.85 D.0.84
B
利用频率估算概率
【变式1】林业部门要考察某种幼树在一定条件下的移植成活率,如图是这种幼树在移植过程中幼树成活率的统计图:
估计该种幼树在此条件下移植成活的概率为________
(结果精确到0.01).
0.88
利用频率估算概率
【变式2】关于频率和概率的关系,下列说法正确的是( )
A. 频率等于概率
B. 当试验次数很大时,频率稳定在概率附近
C. 当试验次数很大时,概率稳定在频率附近
D. 试验得到的频率与概率不可能相同
B
根据频率的稳定性计算
【例4】在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小明通过多次试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球的个数最有可能是( )
A.5 B.10
C.12 D.15
A
根据频率的稳定性计算
【变式】在一个不透明的袋子中有10个除颜色外均相同的小球,通过多次摸球试验后,发现摸到白球的频率稳定在30%,估计袋子中白球有________个.
3
根据频率估算面积
【例5】一个圆形转盘的半径为2 cm,现将转盘分成若干个扇形,并分别相间涂上红、黄两种颜色.转盘转动10 000次,指针指向红色部分有2 500次.估计指针指向红色部分的概率是_______,转盘上黄色部分的面积约是_______.
0.25
3π cm2
根据频率估算面积
【变式】如图1所示,平整的地面上有一个不规则图案(图中阴影部分),小明想了解该图案的面积是多少,他采取了以下办法:用一个长为8m,宽为5m的长方形,将不规则图案围起来,然后在适当位置随机朝长方形区域扔小球,并记录小球落在不规则图案上的次数(小球扔在界线上或长方形区域外不计入试验结果),他将若干次有效试验的结果绘制成了图2所示的折线统计图,由此可估计不规则图案的面积大约是 .
14cm2
根据频率的稳定性设计方案
【例6】小红和小明在操场做游戏,他们先在地上画了半径分别2m和3m的同心圆(如图),蒙上眼在一定距离外向圈内掷小石子,掷中阴影小红胜,否则小明胜,未掷入圈内不算,你来当裁判.你认为游戏公平吗?为什么?
解:不公平,理由:
根据几何概率的求法:掷中阴影小红胜的概率就是阴影区域的面积与总面积的比值;小明胜的概率为小圆面积与总面积的比值,
而计算可得大圆面积为9π,小圆面积为4π.则阴影部分面积为5π,
则阴影部分面积比小圆面积大.
则小红胜的概率大于小明胜的概率,
所以该游戏是不公平的,对小红有利;
根据频率的稳定性设计方案
【变式】在一个不透明的口袋里装有颜色不同的黄、白两种颜色的球共5只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复…下表是活动中的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近______;(精确到0.1)
0.6
根据频率的稳定性设计方案
【变式】在一个不透明的口袋里装有颜色不同的黄、白两种颜色的球共5只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复…下表是活动中的一组统计数据:
(2)试估算口袋中白种颜色的球有多少只?
由(1)摸到白球的概率为0.6,所以可估计口袋中白种颜色的球的个数=5×0.6=3(只);
根据频率的稳定性设计方案
【变式】在一个不透明的口袋里装有颜色不同的黄、白两种颜色的球共5只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复…下表是活动中的一组统计数据:
(3)请你设计一个增(减)袋中白球或黄球球个数的方案,使得从袋中摸出一个球,这只球是黄球的概率大于是白球的概率.
由于现有白球3只,黄球2只,故要使黄球的概率大于是白球的概率,则增加2个以上黄球或减少2个以上白球.
课堂小结
频率与概率
概率
频率与概率的关系
不可能事件A发生的概率是0
随机事件A发生的概率是0和1之间的一个数
必然事件A发生的概率是1
利用频率估计等可能事件的概率
利用频率估计非等可能事件的概率
谢谢收看!
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
