人教版 七年级数学下册 7.1.2 平面直角坐标系 课件 (共34张PPT)
文档属性
| 名称 | 人教版 七年级数学下册 7.1.2 平面直角坐标系 课件 (共34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-05 00:00:00 | ||
图片预览


文档简介
(共34张PPT)
【义务教育教科书人教版七年级下册】
7.1.2 平面直角坐标系
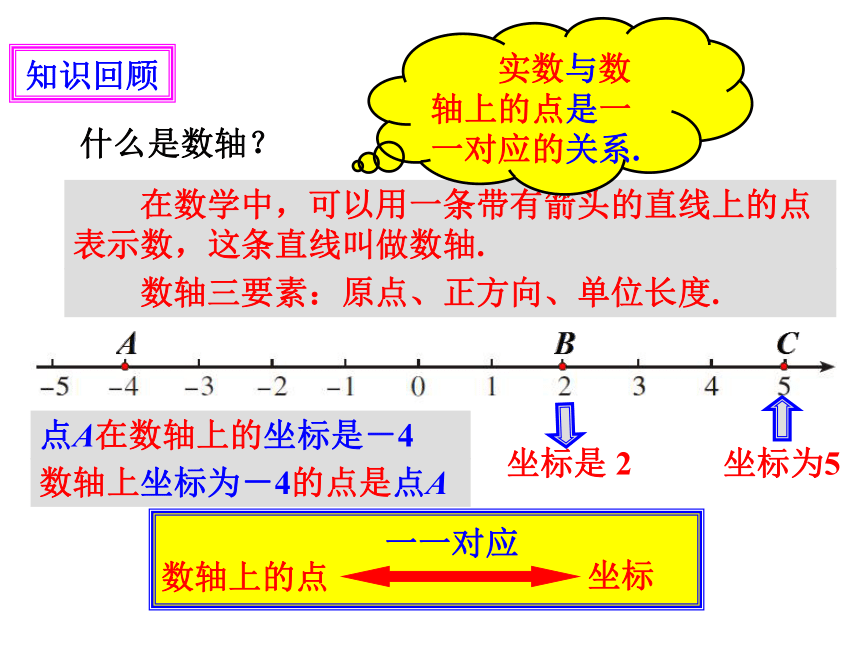
知识回顾
什么是数轴?
在数学中,可以用一条带有箭头的直线上的点表示数,这条直线叫做数轴.
数轴三要素:原点、正方向、单位长度.
实数与数轴上的点是一一对应的关系.
点A在数轴上的坐标是-4
坐标是 2
数轴上坐标为-4的点是点A
坐标为5
数轴上的点
坐标
一一对应
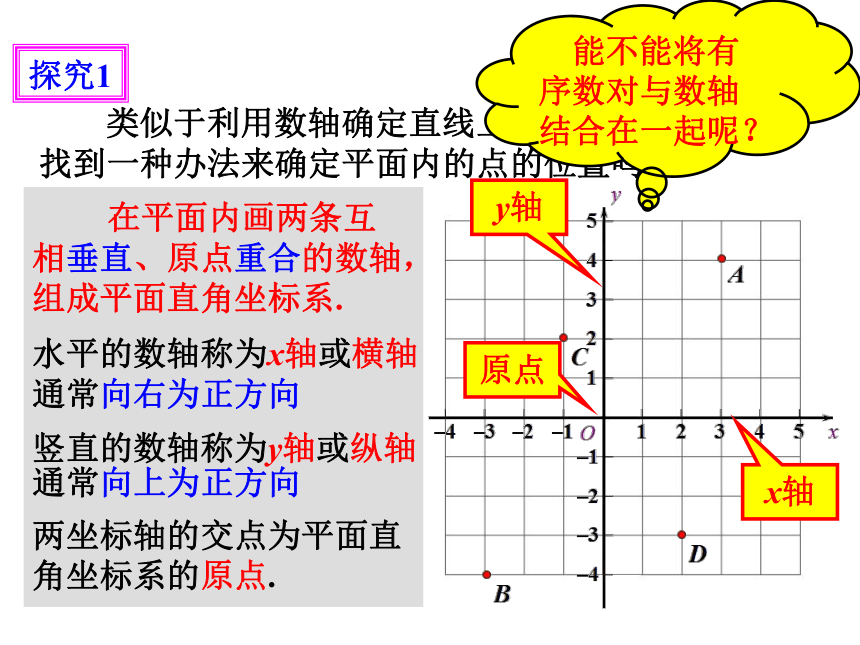
探究1
类似于利用数轴确定直线上点的位置,能不能找到一种办法来确定平面内的点的位置吗?
能不能将有序数对与数轴结合在一起呢?
在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系.
y轴
x轴
原点
水平的数轴称为x轴或横轴
通常向右为正方向
竖直的数轴称为y轴或纵轴
通常向上为正方向
两坐标轴的交点为平面直角坐标系的原点.
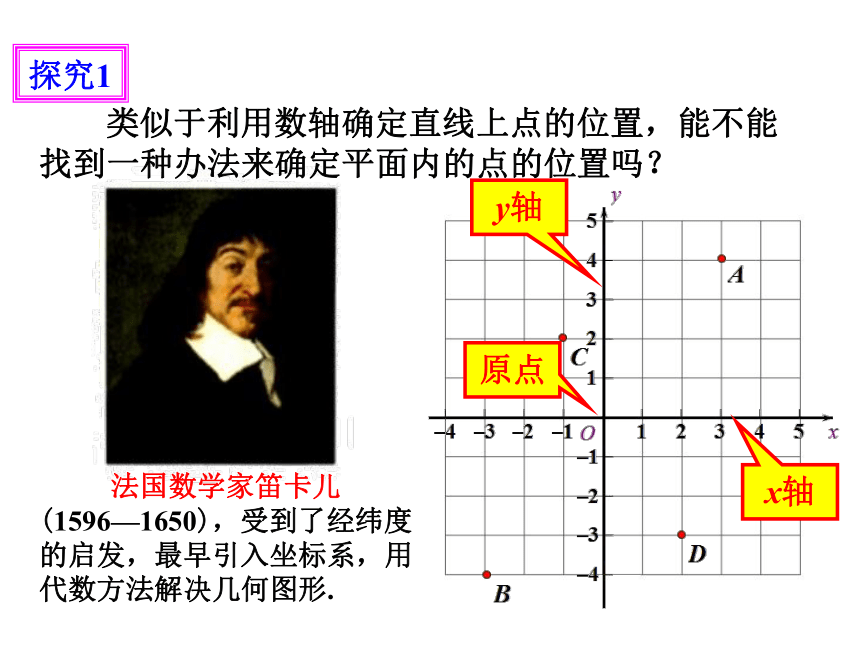
探究1
类似于利用数轴确定直线上点的位置,能不能找到一种办法来确定平面内的点的位置吗?
y轴
x轴
原点
法国数学家笛卡儿(1596—1650),受到了经纬度的启发,最早引入坐标系,用代数方法解决几何图形.
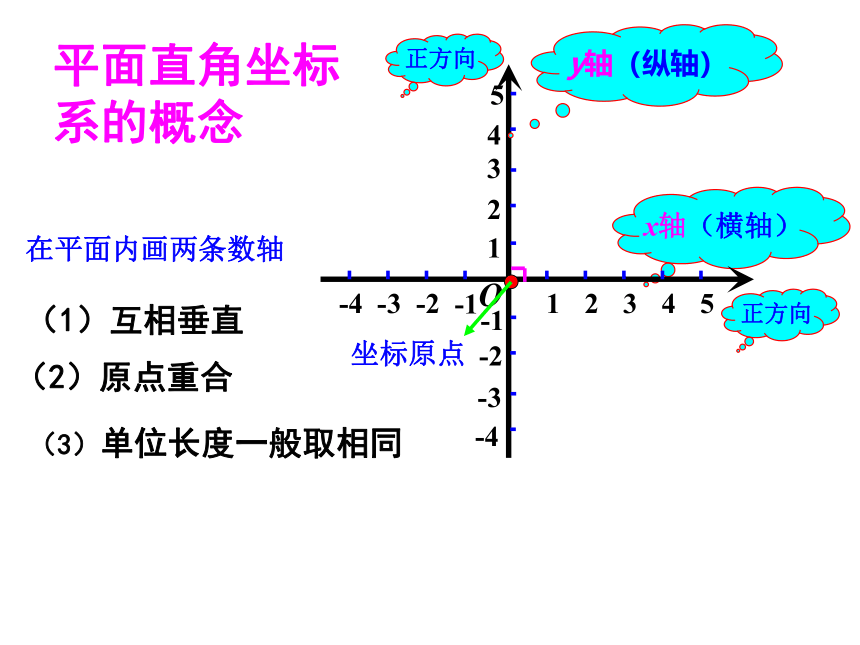
平面直角坐标系的概念
在平面内画两条数轴
(1)互相垂直
(2)原点重合
x轴(横轴)
O
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y轴(纵轴)
坐标原点
(3)单位长度一般取相同
正方向
正方向
问题 数轴上点与其坐标是什么关系?想一想平面上的点与坐标又是什么关系?
数轴上的点与坐标(实数)一一对应.
用类比的方法得到
平面上的点与坐标(有序实数对)也是一一对应的.
( )
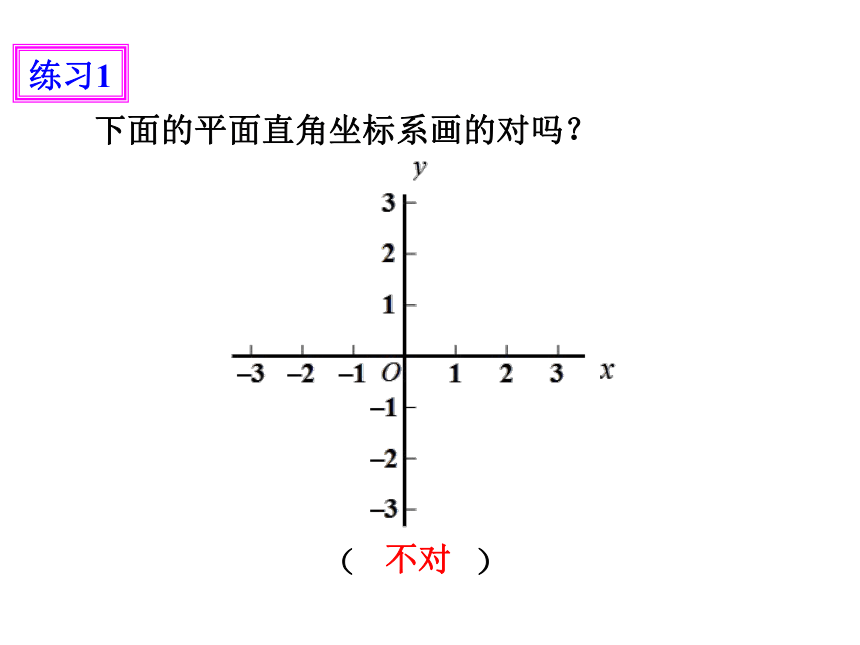
练习1
下面的平面直角坐标系画的对吗?
不对
( )
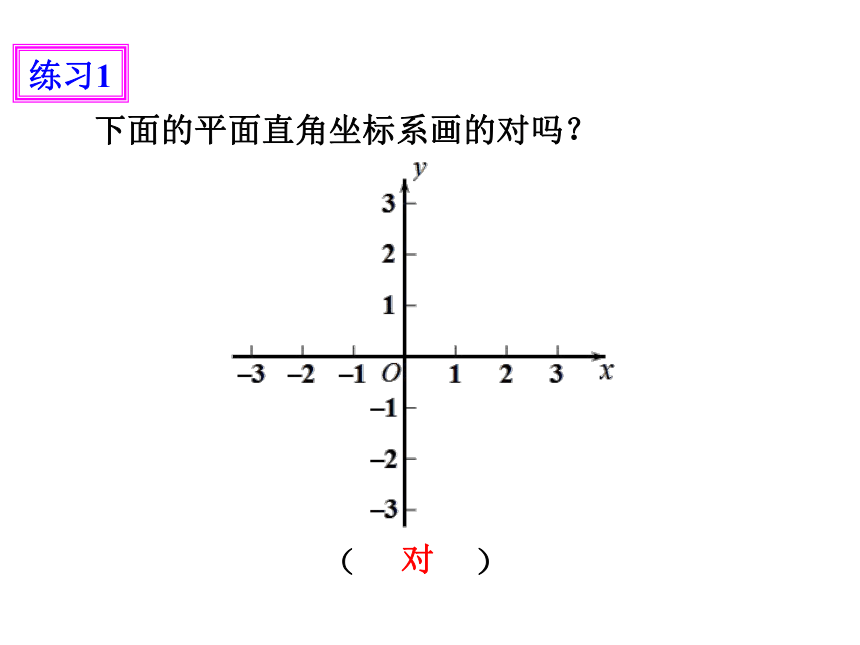
练习1
对
下面的平面直角坐标系画的对吗?
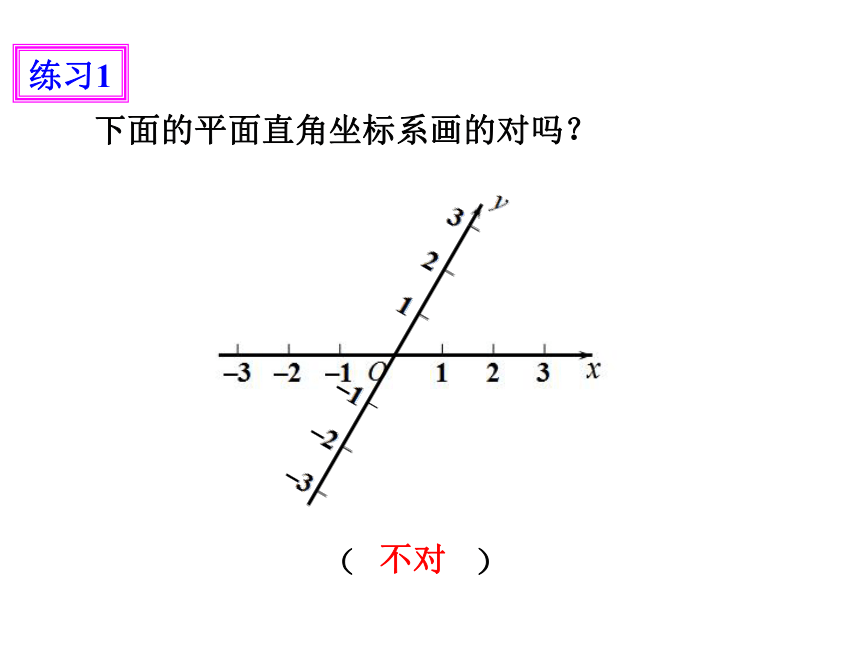
( )
练习1
不对
下面的平面直角坐标系画的对吗?
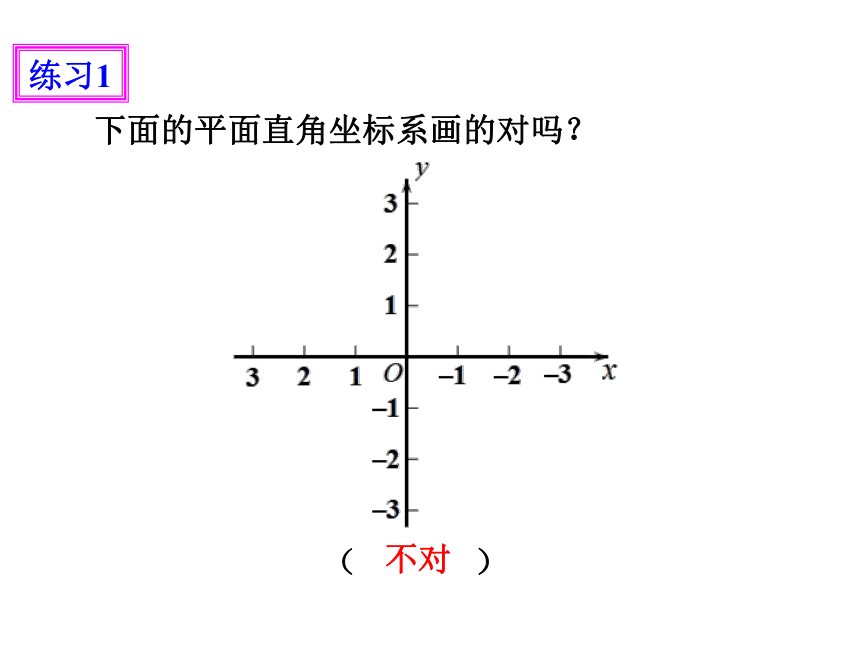
( )
练习1
不对
下面的平面直角坐标系画的对吗?
B(____,____)
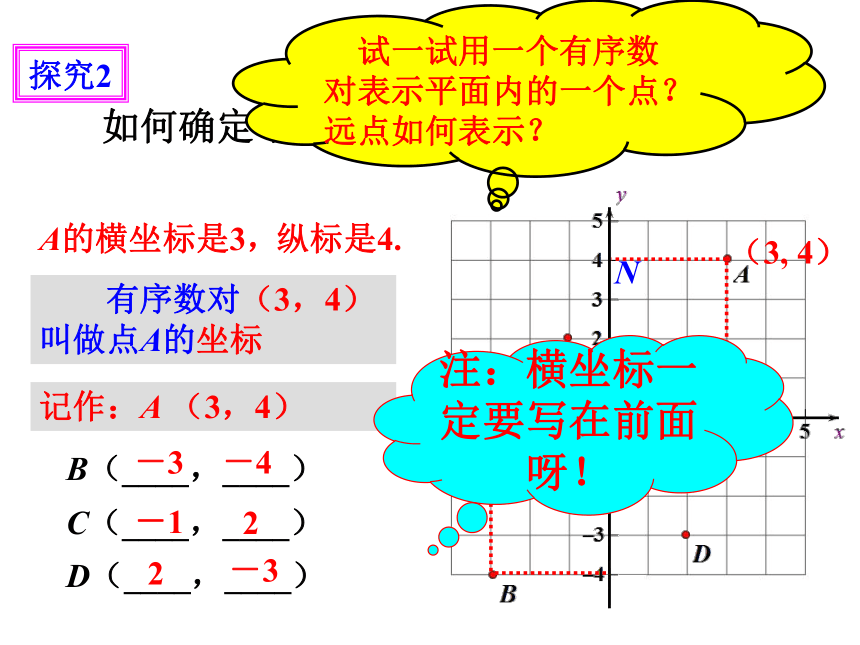
探究2
(3, 4)
-4
M
N
如何确定平面内的点的位置吗?
A的横坐标是3,
纵标是4.
有序数对(3,4)叫做点A的坐标
记作:A (3,4)
试一试用一个有序数对表示平面内的一个点?远点如何表示?
-3
C(____,____)
-1
2
D(____,____)
2
-3
注:横坐标一定要写在前面呀!
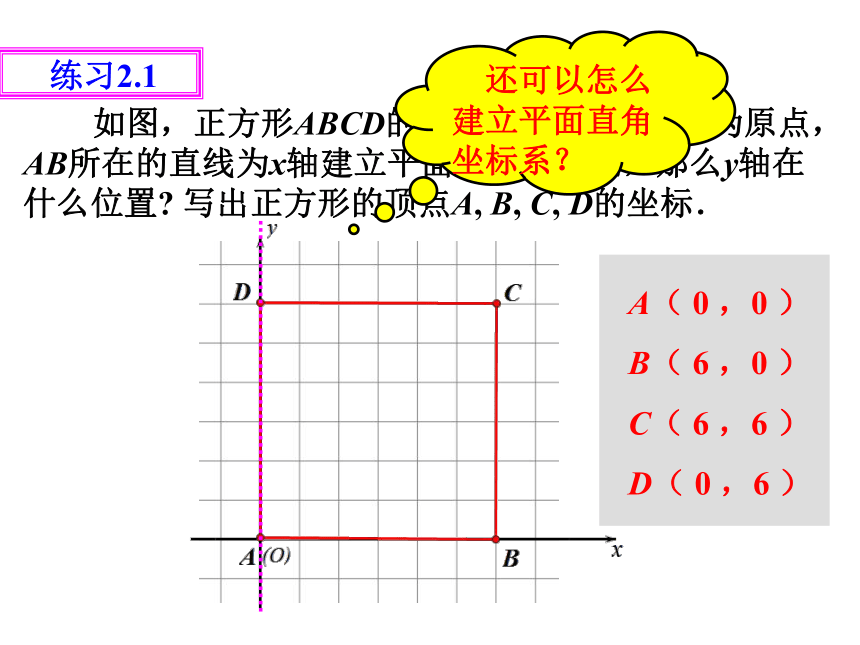
练习2.1
如图,正方形ABCD的边长为6. 如果以点A为原点,AB所在的直线为x轴建立平面直角坐标系,那么y轴在什么位置 写出正方形的顶点A, B, C, D的坐标.
A( 0 ,0 )
B( 6 ,0 )
C( 6 ,6 )
D( 0 ,6 )
还可以怎么建立平面直角坐标系?
练习2.2
如图,正方形ABCD的边长为6.另建立一个平面直角坐标系,此时正方形的顶点A,B,C,D的坐标又分别是什么?
A(-3,-3)
B( 3 ,-3)
C( 3 , 3 )
D(-3 ,3 )
点A到x轴的距离是几个单位长度?
探究3
例:在平面直角坐标系中描出下列各点:
A( 4 , 5 ),
B(-2 , 3 ),
C(-4 ,-1),
D(2.5,-2),
E( 0 ,-4).
( 4 ,5 )
( -2 ,3 )
( -4 ,-1 )
( 2.5 ,-2 )
( 0 ,-4 )
点到两轴的距离
点P(x,y)到x轴的距离为∣y∣,到y轴的距离为∣x∣.例如,点A(-3,4)到x轴的距离为4,到y轴的距离为3.
注意:
点P(x,y)到两轴的距离是一个非负数.
例如:点A(-3,4)到y轴的距离为3
而不是-3
探究3
坐标平面被两条坐标轴分成了Ⅰ,Ⅱ,Ⅲ
,Ⅳ四个部分,每个部分称为象限.
Ⅰ
Ⅱ
Ⅲ
Ⅳ
第一象限
第二象限
第三象限
第四象限
注意:坐标轴上的点不属于任何象限.
探究3
例:在平面直角坐标系中描出下列各点:
A( 4 , 5 ),
B(-2 , 3 ),
C(-4 ,-1),
D(2.5,-2),
E( 0 ,-4).
( 4 ,5 )
( -2 ,3 )
( -4 ,-1 )
( 2.5 ,-2 )
( 0 ,-4 )
各象限点的坐标符号有特点呢?
探究3
Ⅰ
Ⅱ
Ⅲ
Ⅳ
第一象限
第二象限
第三象限
第四象限
(+, +)
(-, +)
(-, -)
(+, -)
(x,y)
平面上的点
坐标
(有序实数对)
一一 对应
探究4
(4, 0)
(-3, 0)
(0,2 )
(0 ,-3)
如图,在平面直角坐标系中,你能分别写出点A,B,C,D的坐标吗?x轴和y轴上的点的坐标有什么特点?原点的坐标是什么?
x轴上的点的纵坐标为0,一般记为(x,0);
y轴上的点的横坐标为0,一般记为(0,y);
原点O的坐标是(0,0).
A(3,6)
B(0,-8)
C(-7,-5)
D(-6,0)
E(-3.6,5)
F(5,-6)
G(0,0)
第一象限
第三象限
第二象限
第四象限
Y 轴上
X 轴上
原点
下列各点分别在坐标平面的什么位置上?
一、判断:
1、对于坐标平面内的任一点,都有唯 一的一对有序实数与它对应.( )
2、在平面直角坐标系内,原点的坐标是0.( )
3、点A(a ,-b )在第二象限,则点B(-a,b)在第四象限. ( )
4、若点P的坐标为(a,b),且a·b=0,则点P一定在坐标原点. ( )
√
√
×
×
练习4
(1)若点P(a,b)在第四象限内,则a,b的取值范围是 ____________________;
a>0,b<0
(2)如果点A(x,y)在第三象限,则点B(-x,y-1)在_________象限;
第四
(3)点P(m+3, m+1)在直角坐标系的x轴上,则点P 坐标为 ____________.
(2 , 0)
1、已知P点坐标为(2a+1,a-3)
①点P在x轴上,则a= ;
②点P在y轴上,则a= ;
③点P在第三象限内,则a的取值范围是 ;
④点P在第四象限内,则a的取值范围是 .
2、若点P(x,y)在第四象限,|x|=5,|y|=4,则P点的坐标为 .(变式)
3
(5,-4)
练习
一、填空
应用提高
A( 3 , 2 )
B( 3 ,-2)
C( 3 ,-3)
D( 3 , 0 )
E( 3 ,-5)
F( 3 , 4 )
1. 在平面直角坐标系上,分别描出下列各点,你有什么发现?
到y轴的距离都是3个单位长度
应用提高
A( 3 , 2 )
B( 4 , 2 )
C( 1 , 2 )
D(-5 , 2 )
E(-3 , 2 )
F(-1, 2 )
2. 在平面直角坐标系上,分别描出下列各点,你有什么发现?
到x轴的距离都是2个单位长度
今天我们学习了哪些知识?
1. 什么是平面直角坐标系?
2. 平面直角坐标系中一个有序数对可以确定一个点的位置,它与数轴上一个实数确定一个点的位置有什么区别?
3. 平面直角坐标系内点与坐标之间有什么关系?
体验收获
平面直角坐标系的概念
在平面内画两条数轴
(1)互相垂直
(2)原点重合
x轴(横轴)
O
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
第一象限
第二象限
第三象限
第四象限
y轴(纵轴)
坐标原点
(3)单位长度一般取相同
Ⅰ
Ⅱ
Ⅲ
Ⅳ
正方向
正方向
1. 数轴上的点与坐标(实数)一一对应.
2. 平面上的点与坐标(有序实数对)也是一一对应的.
1. 数轴上的点与坐标(实数)一一对应.
2. 平面上的点与坐标(有序实数对)也是一一对应的.
达标测评
2.若D、E的坐标分别为:(2,-2)、(-2,-3),请 在图中标出来;
1. 如图所示,请写出A、B、C的坐标:
___________________________;
3.原点O的坐标是(___,___), 横轴上的点的坐标为(x, ___),纵轴上的点的坐标为(___, y)
A(1 , 1 )
B(4 , 3 )
C(-3, 2 )
D(2,-2)
E(-2,-3)
0
0
0
0
达标测评
4. 请你根据下列各点的坐标判定它们分别在第几象限或在什么坐标轴上?
A(-5, 2); B(3,-2); C(0, 4); D(-6, 0); E(1, 8);
F(0, 0); G(5, 0); H(-6,-4); I(0,-3).
解:A在第二象限,
B在第四象限,
C在y轴的正半轴,
E在第一象限,
D在x轴的负半轴,
F在原点,
G在x轴的正半轴,
H在第三象限,
I在y轴的负半轴.
6.点A在x轴上,距离原点4个单位长度,则A点的坐标是__________________.
达标测评
5. 已知点P(3,a),并且P点到x轴的距离是2个单位长度,则P点的坐标为__________________.
分析:由一个点到x轴的距离是该点纵坐标的绝对值,所以a的绝对值等于2,这样a的值应等于±2.
(4, 0)或(-4, 0)
(3, 2)或(3, -2)
二、选择题
(3)如果点 E(a,b)在第二象限,那么点 Q(-a,b+1) 在( ).
A、第四象限 B、第三象限
C、第二象限 D、第一象限
D
(4)直角坐标系中有一点 M(a,b),其中ab=0 ,则 点M的位置在( )
A、原点 B、x轴上 C、y轴上 D、坐标轴上
D
(5)矩形ABCD中,三点的坐标分别是(0,0),(5,0),
(5,3), D点的坐标是( ).
A、(0,5) B、(5,0) C、(0,3) D、(3,0)
C
3、 已知点P( -3 , 2 ),说出点P位置在_______象限.
4、 已知点Q(0,-3),说出点Q的位置在_______.
第二
Y 轴
布置作业
教材69页习题7.1第4、5题.
【义务教育教科书人教版七年级下册】
7.1.2 平面直角坐标系
知识回顾
什么是数轴?
在数学中,可以用一条带有箭头的直线上的点表示数,这条直线叫做数轴.
数轴三要素:原点、正方向、单位长度.
实数与数轴上的点是一一对应的关系.
点A在数轴上的坐标是-4
坐标是 2
数轴上坐标为-4的点是点A
坐标为5
数轴上的点
坐标
一一对应
探究1
类似于利用数轴确定直线上点的位置,能不能找到一种办法来确定平面内的点的位置吗?
能不能将有序数对与数轴结合在一起呢?
在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系.
y轴
x轴
原点
水平的数轴称为x轴或横轴
通常向右为正方向
竖直的数轴称为y轴或纵轴
通常向上为正方向
两坐标轴的交点为平面直角坐标系的原点.
探究1
类似于利用数轴确定直线上点的位置,能不能找到一种办法来确定平面内的点的位置吗?
y轴
x轴
原点
法国数学家笛卡儿(1596—1650),受到了经纬度的启发,最早引入坐标系,用代数方法解决几何图形.
平面直角坐标系的概念
在平面内画两条数轴
(1)互相垂直
(2)原点重合
x轴(横轴)
O
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y轴(纵轴)
坐标原点
(3)单位长度一般取相同
正方向
正方向
问题 数轴上点与其坐标是什么关系?想一想平面上的点与坐标又是什么关系?
数轴上的点与坐标(实数)一一对应.
用类比的方法得到
平面上的点与坐标(有序实数对)也是一一对应的.
( )
练习1
下面的平面直角坐标系画的对吗?
不对
( )
练习1
对
下面的平面直角坐标系画的对吗?
( )
练习1
不对
下面的平面直角坐标系画的对吗?
( )
练习1
不对
下面的平面直角坐标系画的对吗?
B(____,____)
探究2
(3, 4)
-4
M
N
如何确定平面内的点的位置吗?
A的横坐标是3,
纵标是4.
有序数对(3,4)叫做点A的坐标
记作:A (3,4)
试一试用一个有序数对表示平面内的一个点?远点如何表示?
-3
C(____,____)
-1
2
D(____,____)
2
-3
注:横坐标一定要写在前面呀!
练习2.1
如图,正方形ABCD的边长为6. 如果以点A为原点,AB所在的直线为x轴建立平面直角坐标系,那么y轴在什么位置 写出正方形的顶点A, B, C, D的坐标.
A( 0 ,0 )
B( 6 ,0 )
C( 6 ,6 )
D( 0 ,6 )
还可以怎么建立平面直角坐标系?
练习2.2
如图,正方形ABCD的边长为6.另建立一个平面直角坐标系,此时正方形的顶点A,B,C,D的坐标又分别是什么?
A(-3,-3)
B( 3 ,-3)
C( 3 , 3 )
D(-3 ,3 )
点A到x轴的距离是几个单位长度?
探究3
例:在平面直角坐标系中描出下列各点:
A( 4 , 5 ),
B(-2 , 3 ),
C(-4 ,-1),
D(2.5,-2),
E( 0 ,-4).
( 4 ,5 )
( -2 ,3 )
( -4 ,-1 )
( 2.5 ,-2 )
( 0 ,-4 )
点到两轴的距离
点P(x,y)到x轴的距离为∣y∣,到y轴的距离为∣x∣.例如,点A(-3,4)到x轴的距离为4,到y轴的距离为3.
注意:
点P(x,y)到两轴的距离是一个非负数.
例如:点A(-3,4)到y轴的距离为3
而不是-3
探究3
坐标平面被两条坐标轴分成了Ⅰ,Ⅱ,Ⅲ
,Ⅳ四个部分,每个部分称为象限.
Ⅰ
Ⅱ
Ⅲ
Ⅳ
第一象限
第二象限
第三象限
第四象限
注意:坐标轴上的点不属于任何象限.
探究3
例:在平面直角坐标系中描出下列各点:
A( 4 , 5 ),
B(-2 , 3 ),
C(-4 ,-1),
D(2.5,-2),
E( 0 ,-4).
( 4 ,5 )
( -2 ,3 )
( -4 ,-1 )
( 2.5 ,-2 )
( 0 ,-4 )
各象限点的坐标符号有特点呢?
探究3
Ⅰ
Ⅱ
Ⅲ
Ⅳ
第一象限
第二象限
第三象限
第四象限
(+, +)
(-, +)
(-, -)
(+, -)
(x,y)
平面上的点
坐标
(有序实数对)
一一 对应
探究4
(4, 0)
(-3, 0)
(0,2 )
(0 ,-3)
如图,在平面直角坐标系中,你能分别写出点A,B,C,D的坐标吗?x轴和y轴上的点的坐标有什么特点?原点的坐标是什么?
x轴上的点的纵坐标为0,一般记为(x,0);
y轴上的点的横坐标为0,一般记为(0,y);
原点O的坐标是(0,0).
A(3,6)
B(0,-8)
C(-7,-5)
D(-6,0)
E(-3.6,5)
F(5,-6)
G(0,0)
第一象限
第三象限
第二象限
第四象限
Y 轴上
X 轴上
原点
下列各点分别在坐标平面的什么位置上?
一、判断:
1、对于坐标平面内的任一点,都有唯 一的一对有序实数与它对应.( )
2、在平面直角坐标系内,原点的坐标是0.( )
3、点A(a ,-b )在第二象限,则点B(-a,b)在第四象限. ( )
4、若点P的坐标为(a,b),且a·b=0,则点P一定在坐标原点. ( )
√
√
×
×
练习4
(1)若点P(a,b)在第四象限内,则a,b的取值范围是 ____________________;
a>0,b<0
(2)如果点A(x,y)在第三象限,则点B(-x,y-1)在_________象限;
第四
(3)点P(m+3, m+1)在直角坐标系的x轴上,则点P 坐标为 ____________.
(2 , 0)
1、已知P点坐标为(2a+1,a-3)
①点P在x轴上,则a= ;
②点P在y轴上,则a= ;
③点P在第三象限内,则a的取值范围是 ;
④点P在第四象限内,则a的取值范围是 .
2、若点P(x,y)在第四象限,|x|=5,|y|=4,则P点的坐标为 .(变式)
3
(5,-4)
练习
一、填空
应用提高
A( 3 , 2 )
B( 3 ,-2)
C( 3 ,-3)
D( 3 , 0 )
E( 3 ,-5)
F( 3 , 4 )
1. 在平面直角坐标系上,分别描出下列各点,你有什么发现?
到y轴的距离都是3个单位长度
应用提高
A( 3 , 2 )
B( 4 , 2 )
C( 1 , 2 )
D(-5 , 2 )
E(-3 , 2 )
F(-1, 2 )
2. 在平面直角坐标系上,分别描出下列各点,你有什么发现?
到x轴的距离都是2个单位长度
今天我们学习了哪些知识?
1. 什么是平面直角坐标系?
2. 平面直角坐标系中一个有序数对可以确定一个点的位置,它与数轴上一个实数确定一个点的位置有什么区别?
3. 平面直角坐标系内点与坐标之间有什么关系?
体验收获
平面直角坐标系的概念
在平面内画两条数轴
(1)互相垂直
(2)原点重合
x轴(横轴)
O
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
第一象限
第二象限
第三象限
第四象限
y轴(纵轴)
坐标原点
(3)单位长度一般取相同
Ⅰ
Ⅱ
Ⅲ
Ⅳ
正方向
正方向
1. 数轴上的点与坐标(实数)一一对应.
2. 平面上的点与坐标(有序实数对)也是一一对应的.
1. 数轴上的点与坐标(实数)一一对应.
2. 平面上的点与坐标(有序实数对)也是一一对应的.
达标测评
2.若D、E的坐标分别为:(2,-2)、(-2,-3),请 在图中标出来;
1. 如图所示,请写出A、B、C的坐标:
___________________________;
3.原点O的坐标是(___,___), 横轴上的点的坐标为(x, ___),纵轴上的点的坐标为(___, y)
A(1 , 1 )
B(4 , 3 )
C(-3, 2 )
D(2,-2)
E(-2,-3)
0
0
0
0
达标测评
4. 请你根据下列各点的坐标判定它们分别在第几象限或在什么坐标轴上?
A(-5, 2); B(3,-2); C(0, 4); D(-6, 0); E(1, 8);
F(0, 0); G(5, 0); H(-6,-4); I(0,-3).
解:A在第二象限,
B在第四象限,
C在y轴的正半轴,
E在第一象限,
D在x轴的负半轴,
F在原点,
G在x轴的正半轴,
H在第三象限,
I在y轴的负半轴.
6.点A在x轴上,距离原点4个单位长度,则A点的坐标是__________________.
达标测评
5. 已知点P(3,a),并且P点到x轴的距离是2个单位长度,则P点的坐标为__________________.
分析:由一个点到x轴的距离是该点纵坐标的绝对值,所以a的绝对值等于2,这样a的值应等于±2.
(4, 0)或(-4, 0)
(3, 2)或(3, -2)
二、选择题
(3)如果点 E(a,b)在第二象限,那么点 Q(-a,b+1) 在( ).
A、第四象限 B、第三象限
C、第二象限 D、第一象限
D
(4)直角坐标系中有一点 M(a,b),其中ab=0 ,则 点M的位置在( )
A、原点 B、x轴上 C、y轴上 D、坐标轴上
D
(5)矩形ABCD中,三点的坐标分别是(0,0),(5,0),
(5,3), D点的坐标是( ).
A、(0,5) B、(5,0) C、(0,3) D、(3,0)
C
3、 已知点P( -3 , 2 ),说出点P位置在_______象限.
4、 已知点Q(0,-3),说出点Q的位置在_______.
第二
Y 轴
布置作业
教材69页习题7.1第4、5题.
