(人教版)八年级数学下册 17.1勾股定理 学案(含答案)
文档属性
| 名称 | (人教版)八年级数学下册 17.1勾股定理 学案(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 333.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-05 07:54:45 | ||
图片预览



文档简介
第十七章 勾股定理
17.1 勾股定理(基础巩固)
【要点梳理】
要点一、勾股定理
直角三角形两直角边的平方和等于斜边的平方.如果直角三角形的两直角边长分别为,斜边长为,那么.
要点诠释:
(1)勾股定理揭示了一个直角三角形三边之间的数量关系.
(2)利用勾股定理,当设定一条直角边长为未知数后,根据题目已知的线段长可以建立方程求解,这样就将数与形有机地结合起来,达到了解决问题的目的.
(3)理解勾股定理的一些变式:
,, .
要点二、勾股定理的证明
方法一:将四个全等的直角三角形拼成如图(1)所示的正方形.
图(1)中,所以.
方法二:将四个全等的直角三角形拼成如图(2)所示的正方形.
图(2)中,所以.
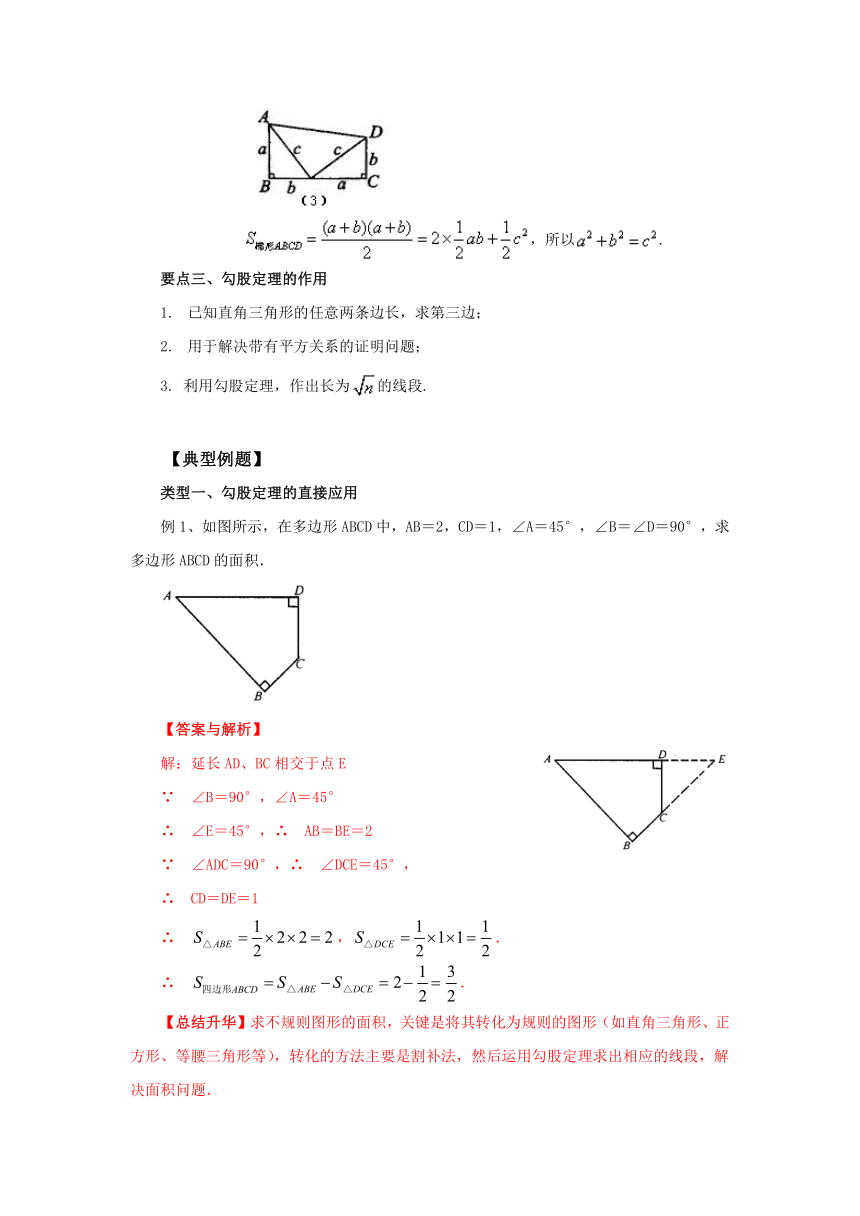
方法三:如图(3)所示,将两个直角三角形拼成直角梯形.
,所以.
要点三、勾股定理的作用
已知直角三角形的任意两条边长,求第三边;
用于解决带有平方关系的证明问题;
3. 利用勾股定理,作出长为的线段.
【典型例题】
类型一、勾股定理的直接应用
例1、如图所示,在多边形ABCD中,AB=2,CD=1,∠A=45°,∠B=∠D=90°,求多边形ABCD的面积.
【答案与解析】
解:延长AD、BC相交于点E
∵ ∠B=90°,∠A=45°
∴ ∠E=45°,∴ AB=BE=2
∵ ∠ADC=90°,∴ ∠DCE=45°,
∴ CD=DE=1
∴ ,.
∴ .
【总结升华】求不规则图形的面积,关键是将其转化为规则的图形(如直角三角形、正方形、等腰三角形等),转化的方法主要是割补法,然后运用勾股定理求出相应的线段,解决面积问题.
举一反三:
【变式】已知:如图,在△ABC,BC=2,S△ABC=3,∠ABC=135°,求AC、AB的长.
【答案】
解:如图,过点A作AD⊥BC交CB的延长线于D,
在△ABC中,∵S△ABC=3,BC=2,
∴AD===3,
∵∠ABC=135°,
∴∠ABD=180°﹣135°=45°,
∴AB=AD=3,
BD=AD=3,
在Rt△ADC中,CD=2+3=5,
由勾股定理得,AC===.
例2、已知直角三角形斜边长为2,周长为,求此三角形的面积.
【思路点拨】欲求Rt△的面积,只需求两直角边之积,而由已知得两直角边之和为,结合勾股定理又得其平方和为4,于是可转化为用方程求解.
【答案与解析】
解:设这个直角三角形的两直角边长分别为,则
即
将①两边平方,得 ③
③-②,得,所以
因此这个直角三角形的面积为.
【总结升华】此题通过设间接未知数,通过变形直接得出的值,而不需要分别求出 的值.本题运用了方程思想解决问题.
例3、长方形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,使点B与点D重合,折痕为EF,求DE的长.
【思路点拨】在折叠的过程中,BE=DE.从而设BE即可表示AE.在直角三角形ADE中,根据勾股定理列方程即可求解.
【答案与解析】
解:设DE=xcm,则BE=DE=x,AE=AB﹣BE=10﹣x,
△ADE中,DE2=AE2+AD2,即x2=(10﹣x)2+16.
∴x=(cm).
答:DE的长为cm.
【总结升华】注意此类题中,要能够发现折叠的对应线段相等.
类型二、利用勾股定理解决实际问题
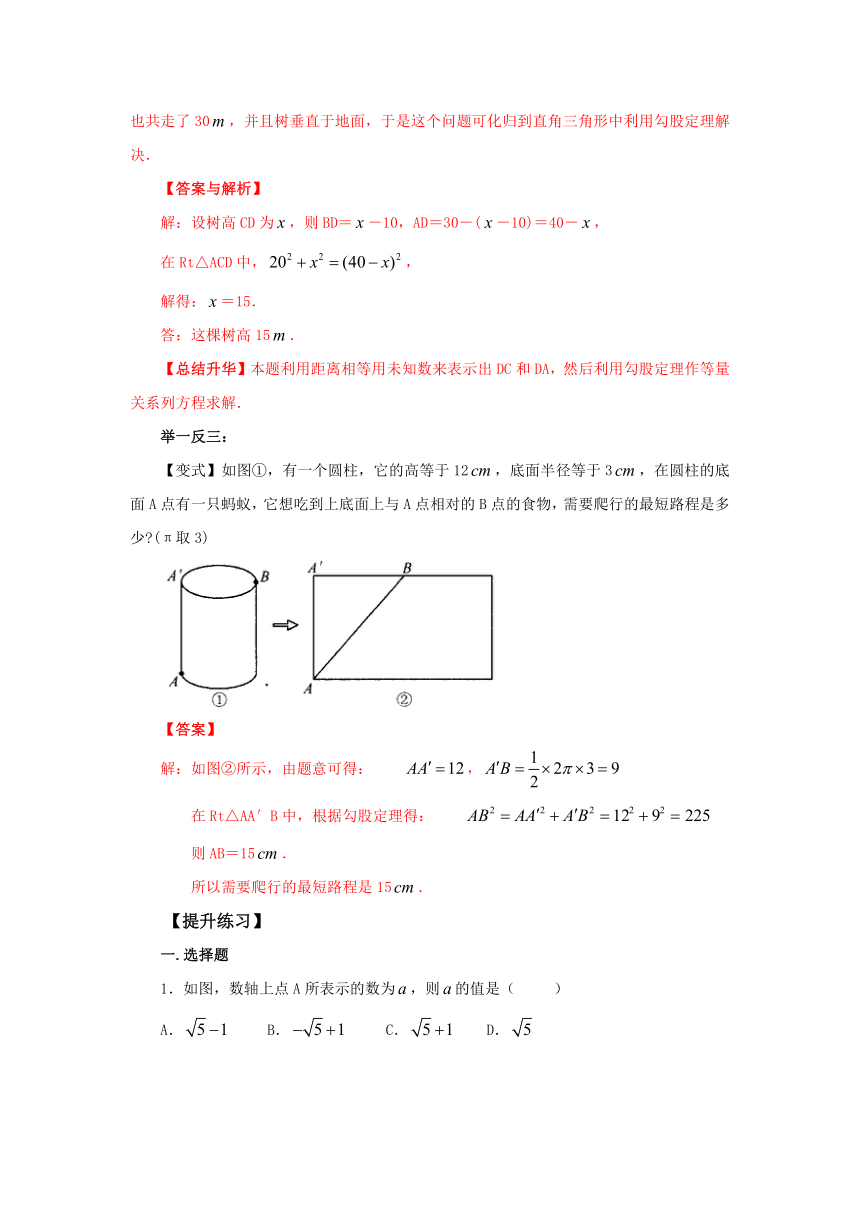
例4、如图所示,在一棵树的10高的B处有两只猴子,一只爬下树走到离树20处的池塘A处,另外一只爬到树顶D后直接跃到A处,距离的直线计算,如果两只猴子所经过的距离相等,试问这棵树有多高?
【思路点拨】其中一只猴子从B→C→A共走了(10+20)=30,另一只猴子从B→D→A也共走了30,并且树垂直于地面,于是这个问题可化归到直角三角形中利用勾股定理解决.
【答案与解析】
解:设树高CD为,则BD=-10,AD=30-(-10)=40-,
在Rt△ACD中,,
解得:=15.
答:这棵树高15.
【总结升华】本题利用距离相等用未知数来表示出DC和DA,然后利用勾股定理作等量关系列方程求解.
举一反三:
【变式】如图①,有一个圆柱,它的高等于12,底面半径等于3,在圆柱的底面A点有一只蚂蚁,它想吃到上底面上与A点相对的B点的食物,需要爬行的最短路程是多少 (π取3)
【答案】
解:如图②所示,由题意可得: ,
在Rt△AA′B中,根据勾股定理得:
则AB=15.
所以需要爬行的最短路程是15.
【提升练习】
一.选择题
1.如图,数轴上点A所表示的数为,则的值是( )
A. B. C. D.
2.如图,所有三角形都是直角三角形,所有四边形都是正方形,已知S1=4,S2=9,S3=8,S4=10,则S=( )
A.25 B.31 C.32 D.40
3. 如图所示,折叠矩形ABCD一边,点D落在BC边的点F处,若AB=8,BC=10,EC的长为( )cm.
A.3 B.4 C.5 D.6
4.如图,长方形AOBC中,点A的坐标为(0,8),点D的纵坐标为3,若将矩形沿直线AD折叠,则顶点C恰好落在边OB上E处,那么图中阴影部分的面积为( )
30 B.32 C.34 D.16
5.如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线,,上,且,之间的距离为2 , ,之间的距离为3 ,则AC的长是( )
A. B. C. D.7
6.在△ABC中,AB=15,AC=13,高AD=12则, △ABC的周长为( )
A.42 B.32 C.42或32 D.37或33
二.填空题
7.若一个直角三角形的两边长分别为12和5,则此三角形的第三边长为______.
8. 如图,将长8,宽4的长方形纸片ABCD折叠,使点A与C重合,则折痕EF的长为__________.
9.在△ABC中,AB=13cm,AC=20cm,BC边上的高为12cm,则△ABC的面积为
cm2.
10. 如图,在平面直角坐标系中,点A,B的坐标分别为(-6,0)、(0,8).以点A为圆心,以AB长为半径画弧,交x正半轴于点C,则点C的坐标为________.
11. 已知长方形ABCD,AB=3,AD=4,过对角线BD的中点O做BD的垂直平分线EF,分别交AD、BC于点E、F,则AE的长为_______________.
12.在直线上依次摆着7个正方形(如图),已知倾斜放置的3个正方形的面积分别为1,2,3,水平放置的4个正方形的面积是则______.
三.解答题
13.如图所示,一架长为2.5米的梯子,斜靠在竖直的墙上,这时梯子的底端距离底0.7米,求梯子顶端离地多少米?如果梯子顶端沿墙下滑0.4m,那么梯子底端将向左滑动多少m?
14. 现有10个边长为1的正方形,排列形式如左下图, 请把它们分割后拼接成一个新的正方形.要求: 在左下图中用实线画出分割线, 并在右下图的正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.
15. 将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=2,P是AC上的一个动点.
(1)当点P在∠ABC的平分线上时,求DP的长;
(2)当点PD=BC时,求此时∠PDA的度数.
【答案与解析】
一.选择题
1.【答案】A;
【解析】-1所表示的点到点A的距离为,OA的距离为.
2.【答案】B;
【解析】解:如图,由题意得:
AB2=S1+S2=13,
AC2=S3+S4=18,
∴BC2=AB2+AC2=31,
∴S=BC2=31,
故选B.
3.【答案】A;
【解析】设CE=,则DE=(8-).在Rt△ABF中,由勾股定理,得BF=6.∴ FC=10-6=4().在Rt△EFC中,由勾股定理,得,即.解得.即EC的长为3.
4.【答案】A;
【解析】由题意CD=DE=5,BE=4,设OE=,AE=AC=,所以,,阴影部分面积为.
5.【答案】A;
【解析】如图,分别作CD⊥交于点E,作AF⊥,则可证△AFB≌△BDC,则AF=3=BD, BF=CD=2+3=5,∴DF=5+3=8=AE,在直角△AEC中,勾股定理得AC=.
6. 【答案】C;
【解析】高在△ABC内部,第三边长为14;高在△ABC外部,第三边长为4,故选C.
二.填空题
7. 【答案】13或;
【解析】没有指明这两边为直角边,所以要分类讨论,12也可能是斜边.
8. 【答案】;
【解析】设AE=EC=,EB=,则,解得,过E点作EH⊥DC于H,EH=4,FH=5-3=2,EF=.
9. 【答案】126或66;
【解析】解:当∠B为锐角时(如图1),
在Rt△ABD中,
BD===5cm,
在Rt△ADC中,
CD===16cm,
∴BC=21,
∴S△ABC==×21×12=126cm2;
当∠B为钝角时(如图2),
在Rt△ABD中,
BD===5cm,
在Rt△ADC中,
CD===16cm,
∴BC=CD﹣BD=16﹣5=11cm,
∴S△ABC==×11×12=66cm2,
故答案为:126或66.
10.【答案】(4,0);
【解析】首先利用勾股定理求出AB的长,进而得到AC的长,因为OC=AC-AO,所以OC求出,继而求出点C的坐标.
11.【答案】;
【解析】连接BE,设AE=,BE=DE=,则,.
12.【答案】4;
【解析】,故.
三.解答题
13.【解析】
解:由题意可得:AB=2.5m,AO=0.7m,
故BO==2.4(m),
∵梯子顶端沿墙下滑0.4m,
∴DO=2m,CD=2.5m,
∴由勾股定理得CO=1.5m,
∴AC=CO﹣AO=1.5﹣0.7=0.8(m).
答:梯子底端将向左滑动0.8m.
14.【解析】
解:如图所示:
15.【解析】
解:(1)连接DP,作DH⊥AC,
在Rt△ABC中,AB=2,∠CAB=30°,∴BC=1,AC=.
∵BP是∠ABC的角平分线,
∴∠CBP=30°,CP=.
在Rt△ADC中,DH=AH=HC=AC=,
∴HP=,
DP=.
(2)当PD=BC=1时,P点的位置可能有两处,分别为,,
在Rt△中,,
所以∠=30°,∠=30°+45°=75°;
同理,∠=45°-30°=15°.
所以∠PDA的度数为15°或75°.
17.1 勾股定理(基础巩固)
【要点梳理】
要点一、勾股定理
直角三角形两直角边的平方和等于斜边的平方.如果直角三角形的两直角边长分别为,斜边长为,那么.
要点诠释:
(1)勾股定理揭示了一个直角三角形三边之间的数量关系.
(2)利用勾股定理,当设定一条直角边长为未知数后,根据题目已知的线段长可以建立方程求解,这样就将数与形有机地结合起来,达到了解决问题的目的.
(3)理解勾股定理的一些变式:
,, .
要点二、勾股定理的证明
方法一:将四个全等的直角三角形拼成如图(1)所示的正方形.
图(1)中,所以.
方法二:将四个全等的直角三角形拼成如图(2)所示的正方形.
图(2)中,所以.
方法三:如图(3)所示,将两个直角三角形拼成直角梯形.
,所以.
要点三、勾股定理的作用
已知直角三角形的任意两条边长,求第三边;
用于解决带有平方关系的证明问题;
3. 利用勾股定理,作出长为的线段.
【典型例题】
类型一、勾股定理的直接应用
例1、如图所示,在多边形ABCD中,AB=2,CD=1,∠A=45°,∠B=∠D=90°,求多边形ABCD的面积.
【答案与解析】
解:延长AD、BC相交于点E
∵ ∠B=90°,∠A=45°
∴ ∠E=45°,∴ AB=BE=2
∵ ∠ADC=90°,∴ ∠DCE=45°,
∴ CD=DE=1
∴ ,.
∴ .
【总结升华】求不规则图形的面积,关键是将其转化为规则的图形(如直角三角形、正方形、等腰三角形等),转化的方法主要是割补法,然后运用勾股定理求出相应的线段,解决面积问题.
举一反三:
【变式】已知:如图,在△ABC,BC=2,S△ABC=3,∠ABC=135°,求AC、AB的长.
【答案】
解:如图,过点A作AD⊥BC交CB的延长线于D,
在△ABC中,∵S△ABC=3,BC=2,
∴AD===3,
∵∠ABC=135°,
∴∠ABD=180°﹣135°=45°,
∴AB=AD=3,
BD=AD=3,
在Rt△ADC中,CD=2+3=5,
由勾股定理得,AC===.
例2、已知直角三角形斜边长为2,周长为,求此三角形的面积.
【思路点拨】欲求Rt△的面积,只需求两直角边之积,而由已知得两直角边之和为,结合勾股定理又得其平方和为4,于是可转化为用方程求解.
【答案与解析】
解:设这个直角三角形的两直角边长分别为,则
即
将①两边平方,得 ③
③-②,得,所以
因此这个直角三角形的面积为.
【总结升华】此题通过设间接未知数,通过变形直接得出的值,而不需要分别求出 的值.本题运用了方程思想解决问题.
例3、长方形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,使点B与点D重合,折痕为EF,求DE的长.
【思路点拨】在折叠的过程中,BE=DE.从而设BE即可表示AE.在直角三角形ADE中,根据勾股定理列方程即可求解.
【答案与解析】
解:设DE=xcm,则BE=DE=x,AE=AB﹣BE=10﹣x,
△ADE中,DE2=AE2+AD2,即x2=(10﹣x)2+16.
∴x=(cm).
答:DE的长为cm.
【总结升华】注意此类题中,要能够发现折叠的对应线段相等.
类型二、利用勾股定理解决实际问题
例4、如图所示,在一棵树的10高的B处有两只猴子,一只爬下树走到离树20处的池塘A处,另外一只爬到树顶D后直接跃到A处,距离的直线计算,如果两只猴子所经过的距离相等,试问这棵树有多高?
【思路点拨】其中一只猴子从B→C→A共走了(10+20)=30,另一只猴子从B→D→A也共走了30,并且树垂直于地面,于是这个问题可化归到直角三角形中利用勾股定理解决.
【答案与解析】
解:设树高CD为,则BD=-10,AD=30-(-10)=40-,
在Rt△ACD中,,
解得:=15.
答:这棵树高15.
【总结升华】本题利用距离相等用未知数来表示出DC和DA,然后利用勾股定理作等量关系列方程求解.
举一反三:
【变式】如图①,有一个圆柱,它的高等于12,底面半径等于3,在圆柱的底面A点有一只蚂蚁,它想吃到上底面上与A点相对的B点的食物,需要爬行的最短路程是多少 (π取3)
【答案】
解:如图②所示,由题意可得: ,
在Rt△AA′B中,根据勾股定理得:
则AB=15.
所以需要爬行的最短路程是15.
【提升练习】
一.选择题
1.如图,数轴上点A所表示的数为,则的值是( )
A. B. C. D.
2.如图,所有三角形都是直角三角形,所有四边形都是正方形,已知S1=4,S2=9,S3=8,S4=10,则S=( )
A.25 B.31 C.32 D.40
3. 如图所示,折叠矩形ABCD一边,点D落在BC边的点F处,若AB=8,BC=10,EC的长为( )cm.
A.3 B.4 C.5 D.6
4.如图,长方形AOBC中,点A的坐标为(0,8),点D的纵坐标为3,若将矩形沿直线AD折叠,则顶点C恰好落在边OB上E处,那么图中阴影部分的面积为( )
30 B.32 C.34 D.16
5.如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线,,上,且,之间的距离为2 , ,之间的距离为3 ,则AC的长是( )
A. B. C. D.7
6.在△ABC中,AB=15,AC=13,高AD=12则, △ABC的周长为( )
A.42 B.32 C.42或32 D.37或33
二.填空题
7.若一个直角三角形的两边长分别为12和5,则此三角形的第三边长为______.
8. 如图,将长8,宽4的长方形纸片ABCD折叠,使点A与C重合,则折痕EF的长为__________.
9.在△ABC中,AB=13cm,AC=20cm,BC边上的高为12cm,则△ABC的面积为
cm2.
10. 如图,在平面直角坐标系中,点A,B的坐标分别为(-6,0)、(0,8).以点A为圆心,以AB长为半径画弧,交x正半轴于点C,则点C的坐标为________.
11. 已知长方形ABCD,AB=3,AD=4,过对角线BD的中点O做BD的垂直平分线EF,分别交AD、BC于点E、F,则AE的长为_______________.
12.在直线上依次摆着7个正方形(如图),已知倾斜放置的3个正方形的面积分别为1,2,3,水平放置的4个正方形的面积是则______.
三.解答题
13.如图所示,一架长为2.5米的梯子,斜靠在竖直的墙上,这时梯子的底端距离底0.7米,求梯子顶端离地多少米?如果梯子顶端沿墙下滑0.4m,那么梯子底端将向左滑动多少m?
14. 现有10个边长为1的正方形,排列形式如左下图, 请把它们分割后拼接成一个新的正方形.要求: 在左下图中用实线画出分割线, 并在右下图的正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.
15. 将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=2,P是AC上的一个动点.
(1)当点P在∠ABC的平分线上时,求DP的长;
(2)当点PD=BC时,求此时∠PDA的度数.
【答案与解析】
一.选择题
1.【答案】A;
【解析】-1所表示的点到点A的距离为,OA的距离为.
2.【答案】B;
【解析】解:如图,由题意得:
AB2=S1+S2=13,
AC2=S3+S4=18,
∴BC2=AB2+AC2=31,
∴S=BC2=31,
故选B.
3.【答案】A;
【解析】设CE=,则DE=(8-).在Rt△ABF中,由勾股定理,得BF=6.∴ FC=10-6=4().在Rt△EFC中,由勾股定理,得,即.解得.即EC的长为3.
4.【答案】A;
【解析】由题意CD=DE=5,BE=4,设OE=,AE=AC=,所以,,阴影部分面积为.
5.【答案】A;
【解析】如图,分别作CD⊥交于点E,作AF⊥,则可证△AFB≌△BDC,则AF=3=BD, BF=CD=2+3=5,∴DF=5+3=8=AE,在直角△AEC中,勾股定理得AC=.
6. 【答案】C;
【解析】高在△ABC内部,第三边长为14;高在△ABC外部,第三边长为4,故选C.
二.填空题
7. 【答案】13或;
【解析】没有指明这两边为直角边,所以要分类讨论,12也可能是斜边.
8. 【答案】;
【解析】设AE=EC=,EB=,则,解得,过E点作EH⊥DC于H,EH=4,FH=5-3=2,EF=.
9. 【答案】126或66;
【解析】解:当∠B为锐角时(如图1),
在Rt△ABD中,
BD===5cm,
在Rt△ADC中,
CD===16cm,
∴BC=21,
∴S△ABC==×21×12=126cm2;
当∠B为钝角时(如图2),
在Rt△ABD中,
BD===5cm,
在Rt△ADC中,
CD===16cm,
∴BC=CD﹣BD=16﹣5=11cm,
∴S△ABC==×11×12=66cm2,
故答案为:126或66.
10.【答案】(4,0);
【解析】首先利用勾股定理求出AB的长,进而得到AC的长,因为OC=AC-AO,所以OC求出,继而求出点C的坐标.
11.【答案】;
【解析】连接BE,设AE=,BE=DE=,则,.
12.【答案】4;
【解析】,故.
三.解答题
13.【解析】
解:由题意可得:AB=2.5m,AO=0.7m,
故BO==2.4(m),
∵梯子顶端沿墙下滑0.4m,
∴DO=2m,CD=2.5m,
∴由勾股定理得CO=1.5m,
∴AC=CO﹣AO=1.5﹣0.7=0.8(m).
答:梯子底端将向左滑动0.8m.
14.【解析】
解:如图所示:
15.【解析】
解:(1)连接DP,作DH⊥AC,
在Rt△ABC中,AB=2,∠CAB=30°,∴BC=1,AC=.
∵BP是∠ABC的角平分线,
∴∠CBP=30°,CP=.
在Rt△ADC中,DH=AH=HC=AC=,
∴HP=,
DP=.
(2)当PD=BC=1时,P点的位置可能有两处,分别为,,
在Rt△中,,
所以∠=30°,∠=30°+45°=75°;
同理,∠=45°-30°=15°.
所以∠PDA的度数为15°或75°.
