人教版六年级下册数学 3.1.2圆柱的表面积(二)(例4) 课件(25张PPT)
文档属性
| 名称 | 人教版六年级下册数学 3.1.2圆柱的表面积(二)(例4) 课件(25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-03 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
六年级下册—人教版—数学—第三单元
圆柱的表面积(二)(例4)
学习准备
图片来自网络
学习目标
进一步理解并掌握圆柱表面积计算方法。
灵活运用圆柱表面积的有关知识解决实际问题,体会数学与生活的密切联系。
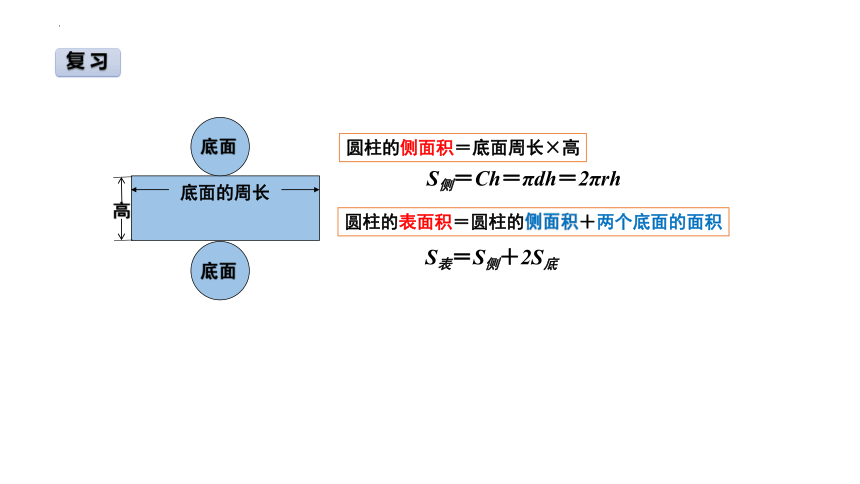
复 习
底面的周长
圆柱的表面积=圆柱的侧面积+两个底面的面积
圆柱的侧面积=底面周长×高
S侧=Ch=πdh=2πrh
S表=S侧+2S底
底面
底面
高
(1)笔袋的侧面积:2×3.14×2×13=163.28(cm )
复 习
做这样一个圆柱形笔袋至少需要多少平方厘米的面料?
13cm
2cm
C
答:至少需要188.4cm 的面料。
侧面积
底面积
2个
笔袋的侧面
笔袋的底面
(2)笔袋的2个底面积:3.14×2 ×2=25.12(cm )
(3)需要用的面料:163.28+25.12=188.4(cm )
h
S底
就是求笔袋的......
例4
(数学书第22页)
20cm
30cm
就是求帽子的......
一顶圆柱形厨师帽,高30cm,帽顶直径20cm。做这样一顶帽子至少需要多少平方厘米的面料?(得数保留整十数。)
侧面积
底面积
1个
(1)帽子的侧面积:
(2)帽顶的面积:
帽子的侧面
帽顶
(3)需要用的面料:
3.14×20×30=1884(cm )
3.14×(20÷2)2=314(cm )
1884+314=2198
≈
(cm )
C
h
r
30cm
?
例4
20cm
30cm
(数学书第22页)
一顶圆柱形厨师帽,高30cm,帽顶直径20cm。做这样一顶帽子至少需要多少平方厘米的面料?(得数保留整十数。)
就是求帽子的......
我用去尾法,得到2190。
我用进一法,2198≈2200。
(3)需要用的面料:
1884+314=2198
≈
(cm )
?
如果得数不是2198,而是2193呢?
例4
一顶圆柱形厨师帽,高30cm,帽顶直径20cm。做这样一顶帽子至少需要多少平方厘米的面料?(得数保留整十数。)
我用四舍五入法,也得到2200。
2200
实际使用的面料要比计算的结果多一些,所以用“进一法”取近似值。
(数学书第22页)
小花
小红
小东
答:至少需要2200cm 的面料。
侧面积
底面积
1个
(1)帽子的侧面积:
(2)帽顶的面积:
帽子的侧面
帽顶
(3)需要用的面料:
3.14×20×30=1884(cm )
3.14×(20÷2)2=314(cm )
1884+314=2198
≈
(cm )
C
h
r
30cm
例4
一顶圆柱形厨师帽,高30cm,帽顶直径20cm。做这样一顶帽子至少需要多少平方厘米的面料?(得数保留整十数。)
(数学书第22页)
20cm
30cm
2200
根据实际问题选用合适的求近似值的方法。
把生活问题转化为圆柱知识进行解决。
回顾
刚才解决问题的过程中,有什么要注意的地方?
侧面积
底面积
1个
(1)帽子的侧面积:
(2)帽顶的面积:
帽子的侧面
帽顶
(3)需要用的面料:
3.14×20×30=1884(cm )
3.14×(20÷2)2=314(cm )
1884+314=2198
≈2200
(cm )
30cm
例4
一顶圆柱形厨师帽,高30cm,帽顶直径20cm。做这样一顶帽子至少
需要多少平方厘米的面料?(得数保留整十数。)
20cm
30cm
回顾刚才解决问题的过程,你发现有什么相同和不同的地方?
生活问题
数学问题
圆柱表面积相关知识解决问题
比一比
(选择正确的答案)修建一个圆柱形的沼气池,底面直径是3m,深2m。在池的侧面与下底面抹上水泥,抹水泥部分的面积是多少平方米?这是求( ) 。
D
(改编自数学书第23页第4题)
A.1个侧面积
B.1个底面积
C.2个底面积
D.1个侧面积+1个底面积
E.1个侧面积+2个底面积
练习
侧面
底面
练习
(选择正确的答案)王阿姨做了一个圆柱形的抱枕,长80厘米,底面直径18厘米,如果侧面用花布,底面用黄色的布。
S侧
S底
(改编自数学书第24页第8题)
(1)花布用了多少,是求( )。
(2)黄布用了多少,是求( )。
(3)一共用了多少布料,是求( )。
A
C
E
A.1个侧面积
B.1个底面积
C.2个底面积
D.1个侧面积+1个底面积
E.1个侧面积+2个底面积
一顶帽子,上面是圆柱形,用黑布做;帽檐部分是一个圆环,用红布做。做这顶帽子,哪种颜色的布用得多
两种颜色的布分别对应哪部分?
每部分是什么图形?
(数学书第23页第7题)
练习
黑布
红布
和 比较
20
10
10
单位:cm
黑布:
红布:
1个底面积+圆柱侧面积
圆环的面积
20
10
10
20
练习
一顶帽子,上面是圆柱形,用黑布做;帽檐部分是一个圆环,用红布做。做这顶帽子,哪种颜色的布用得多
(数学书第23页第7题)
20
10
10
单位:cm
和 比较
黑布
红布
黑布的面积:
3.14×(20÷2) +3.14×20×10=942(cm )
红布的面积:
3.14×[(20÷2+10) -(20÷2) ]=942(cm )
S底
S侧
R
r
黑布的面积=红布的面积
答:两种颜色的布同样多。
练习
一顶帽子,上面是圆柱形,用黑布做;帽檐部分是一个圆环,用红布做。做这顶帽子,哪种颜色的布用得多
(数学书第23页第7题)
和 比较
黑布
红布
一个圆柱形的礼品盒,它的侧面展开是一个长12.56厘米,宽10厘米的长方形。那么这个礼品盒的表面积是多少呢?
礼
品
盒
10cm
12.56cm
对照侧面展开图,你能找到12.56厘米和10厘米在圆柱的什么部分吗?
10cm
C=12.56cm
长方形的长=圆柱的底面周长
长方形的宽=圆柱的高
练习
侧面积:
12.56×10=125.6(cm )
底面半径:
12.56÷3.14÷2=2(cm)
2个底面积:
3.14×2 ×2=25.12(cm )
表面积:
125.6+25.12=150.72(cm )
答:礼品盒的表面积是150.72cm 。
一个圆柱形的礼品盒,它的侧面展开是一个长12.56厘米,宽10厘米的长方形。那么这个礼品盒的表面积是多少呢?
练习
礼
品
盒
10cm
12.56cm
10cm
C=12.56cm
回顾刚才解决问题的过程,你发现有什么相同和不同的地方?
比一比
圆柱、长方体、正方体计算表面积的方法之间有什么联系?
比一比
侧面
S表=S侧+2S底
底面
底面
底面
底面
底面
底面
侧面
侧面
比一比
阅读书本
(数学书第22页)
这节课你有什么收获?
全课总结
需要根据具体情况,确定求哪些面的面积之和。
现实生活中有关表面积计算的情形是复杂多变的。
在计算的时候,要注意找准相关数据。
课后作业:
1.复习数学书第22页例4。
2.完成数学书第22页第2题,第23页第5题。
谢谢观看!
六年级下册—人教版—数学—第三单元
圆柱的表面积(二)(例4)
学习准备
图片来自网络
学习目标
进一步理解并掌握圆柱表面积计算方法。
灵活运用圆柱表面积的有关知识解决实际问题,体会数学与生活的密切联系。
复 习
底面的周长
圆柱的表面积=圆柱的侧面积+两个底面的面积
圆柱的侧面积=底面周长×高
S侧=Ch=πdh=2πrh
S表=S侧+2S底
底面
底面
高
(1)笔袋的侧面积:2×3.14×2×13=163.28(cm )
复 习
做这样一个圆柱形笔袋至少需要多少平方厘米的面料?
13cm
2cm
C
答:至少需要188.4cm 的面料。
侧面积
底面积
2个
笔袋的侧面
笔袋的底面
(2)笔袋的2个底面积:3.14×2 ×2=25.12(cm )
(3)需要用的面料:163.28+25.12=188.4(cm )
h
S底
就是求笔袋的......
例4
(数学书第22页)
20cm
30cm
就是求帽子的......
一顶圆柱形厨师帽,高30cm,帽顶直径20cm。做这样一顶帽子至少需要多少平方厘米的面料?(得数保留整十数。)
侧面积
底面积
1个
(1)帽子的侧面积:
(2)帽顶的面积:
帽子的侧面
帽顶
(3)需要用的面料:
3.14×20×30=1884(cm )
3.14×(20÷2)2=314(cm )
1884+314=2198
≈
(cm )
C
h
r
30cm
?
例4
20cm
30cm
(数学书第22页)
一顶圆柱形厨师帽,高30cm,帽顶直径20cm。做这样一顶帽子至少需要多少平方厘米的面料?(得数保留整十数。)
就是求帽子的......
我用去尾法,得到2190。
我用进一法,2198≈2200。
(3)需要用的面料:
1884+314=2198
≈
(cm )
?
如果得数不是2198,而是2193呢?
例4
一顶圆柱形厨师帽,高30cm,帽顶直径20cm。做这样一顶帽子至少需要多少平方厘米的面料?(得数保留整十数。)
我用四舍五入法,也得到2200。
2200
实际使用的面料要比计算的结果多一些,所以用“进一法”取近似值。
(数学书第22页)
小花
小红
小东
答:至少需要2200cm 的面料。
侧面积
底面积
1个
(1)帽子的侧面积:
(2)帽顶的面积:
帽子的侧面
帽顶
(3)需要用的面料:
3.14×20×30=1884(cm )
3.14×(20÷2)2=314(cm )
1884+314=2198
≈
(cm )
C
h
r
30cm
例4
一顶圆柱形厨师帽,高30cm,帽顶直径20cm。做这样一顶帽子至少需要多少平方厘米的面料?(得数保留整十数。)
(数学书第22页)
20cm
30cm
2200
根据实际问题选用合适的求近似值的方法。
把生活问题转化为圆柱知识进行解决。
回顾
刚才解决问题的过程中,有什么要注意的地方?
侧面积
底面积
1个
(1)帽子的侧面积:
(2)帽顶的面积:
帽子的侧面
帽顶
(3)需要用的面料:
3.14×20×30=1884(cm )
3.14×(20÷2)2=314(cm )
1884+314=2198
≈2200
(cm )
30cm
例4
一顶圆柱形厨师帽,高30cm,帽顶直径20cm。做这样一顶帽子至少
需要多少平方厘米的面料?(得数保留整十数。)
20cm
30cm
回顾刚才解决问题的过程,你发现有什么相同和不同的地方?
生活问题
数学问题
圆柱表面积相关知识解决问题
比一比
(选择正确的答案)修建一个圆柱形的沼气池,底面直径是3m,深2m。在池的侧面与下底面抹上水泥,抹水泥部分的面积是多少平方米?这是求( ) 。
D
(改编自数学书第23页第4题)
A.1个侧面积
B.1个底面积
C.2个底面积
D.1个侧面积+1个底面积
E.1个侧面积+2个底面积
练习
侧面
底面
练习
(选择正确的答案)王阿姨做了一个圆柱形的抱枕,长80厘米,底面直径18厘米,如果侧面用花布,底面用黄色的布。
S侧
S底
(改编自数学书第24页第8题)
(1)花布用了多少,是求( )。
(2)黄布用了多少,是求( )。
(3)一共用了多少布料,是求( )。
A
C
E
A.1个侧面积
B.1个底面积
C.2个底面积
D.1个侧面积+1个底面积
E.1个侧面积+2个底面积
一顶帽子,上面是圆柱形,用黑布做;帽檐部分是一个圆环,用红布做。做这顶帽子,哪种颜色的布用得多
两种颜色的布分别对应哪部分?
每部分是什么图形?
(数学书第23页第7题)
练习
黑布
红布
和 比较
20
10
10
单位:cm
黑布:
红布:
1个底面积+圆柱侧面积
圆环的面积
20
10
10
20
练习
一顶帽子,上面是圆柱形,用黑布做;帽檐部分是一个圆环,用红布做。做这顶帽子,哪种颜色的布用得多
(数学书第23页第7题)
20
10
10
单位:cm
和 比较
黑布
红布
黑布的面积:
3.14×(20÷2) +3.14×20×10=942(cm )
红布的面积:
3.14×[(20÷2+10) -(20÷2) ]=942(cm )
S底
S侧
R
r
黑布的面积=红布的面积
答:两种颜色的布同样多。
练习
一顶帽子,上面是圆柱形,用黑布做;帽檐部分是一个圆环,用红布做。做这顶帽子,哪种颜色的布用得多
(数学书第23页第7题)
和 比较
黑布
红布
一个圆柱形的礼品盒,它的侧面展开是一个长12.56厘米,宽10厘米的长方形。那么这个礼品盒的表面积是多少呢?
礼
品
盒
10cm
12.56cm
对照侧面展开图,你能找到12.56厘米和10厘米在圆柱的什么部分吗?
10cm
C=12.56cm
长方形的长=圆柱的底面周长
长方形的宽=圆柱的高
练习
侧面积:
12.56×10=125.6(cm )
底面半径:
12.56÷3.14÷2=2(cm)
2个底面积:
3.14×2 ×2=25.12(cm )
表面积:
125.6+25.12=150.72(cm )
答:礼品盒的表面积是150.72cm 。
一个圆柱形的礼品盒,它的侧面展开是一个长12.56厘米,宽10厘米的长方形。那么这个礼品盒的表面积是多少呢?
练习
礼
品
盒
10cm
12.56cm
10cm
C=12.56cm
回顾刚才解决问题的过程,你发现有什么相同和不同的地方?
比一比
圆柱、长方体、正方体计算表面积的方法之间有什么联系?
比一比
侧面
S表=S侧+2S底
底面
底面
底面
底面
底面
底面
侧面
侧面
比一比
阅读书本
(数学书第22页)
这节课你有什么收获?
全课总结
需要根据具体情况,确定求哪些面的面积之和。
现实生活中有关表面积计算的情形是复杂多变的。
在计算的时候,要注意找准相关数据。
课后作业:
1.复习数学书第22页例4。
2.完成数学书第22页第2题,第23页第5题。
谢谢观看!
