人教版六年级下学期数学3.1.2圆柱的表面积(一)(例3)课件(共37张PPT)
文档属性
| 名称 | 人教版六年级下学期数学3.1.2圆柱的表面积(一)(例3)课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-04 06:36:43 | ||
图片预览


文档简介
(共35张PPT)
六年级下册—人教版—数学—第三单元
圆柱的表面积(一)(例3)
理解圆柱的表面积的含义。
探究并掌握圆柱侧面积及表面积的计算方法。
会计算圆柱的侧面积和表面积,并解决简单的实际问题。
学习目标
复习回顾
圆柱
长方体
正方体
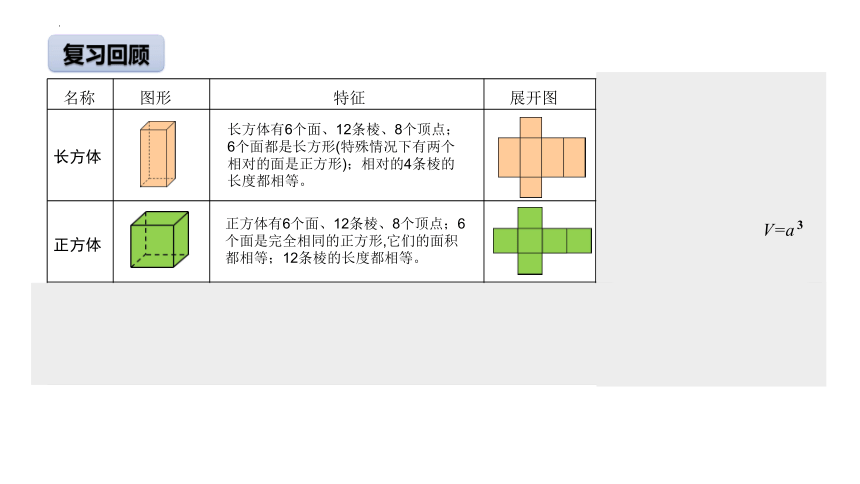
长方体有6个面、12条棱、8个顶点;6个面都是长方形(特殊情况下有两个相对的面是正方形);相对的4条棱的长度都相等。
正方体有6个面、12条棱、8个顶点;6个面是完全相同的正方形,它们的面积都相等;12条棱的长度都相等。
圆柱的两个底面是完全相同的两个圆,侧面是一个曲面,两个底面之间的距离叫做圆柱的高。
S =2(ab+ah+bh)
S =6a
名称
图形
特征
展开图
表面积
体积
?
表
表
2
圆柱的表面积指的是什么?怎样计算呢?
V=abh
V=Sh
V=Sh
V=a
3
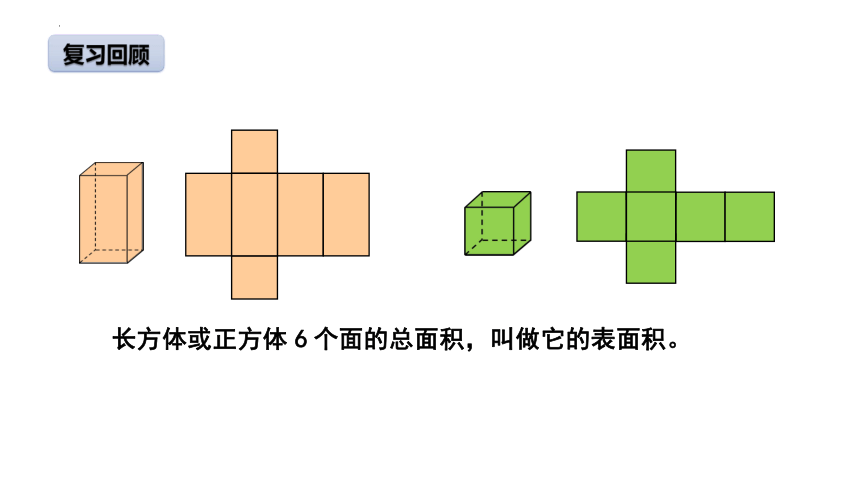
长方体或正方体 6 个面的总面积,叫做它的表面积。
复习回顾
底面
底面
底面
底面
底面的周长
底面的周长
高
高
侧面
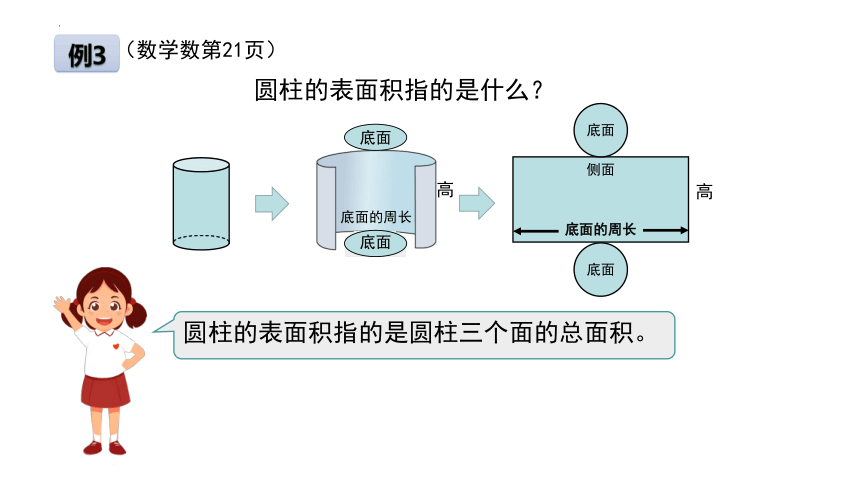
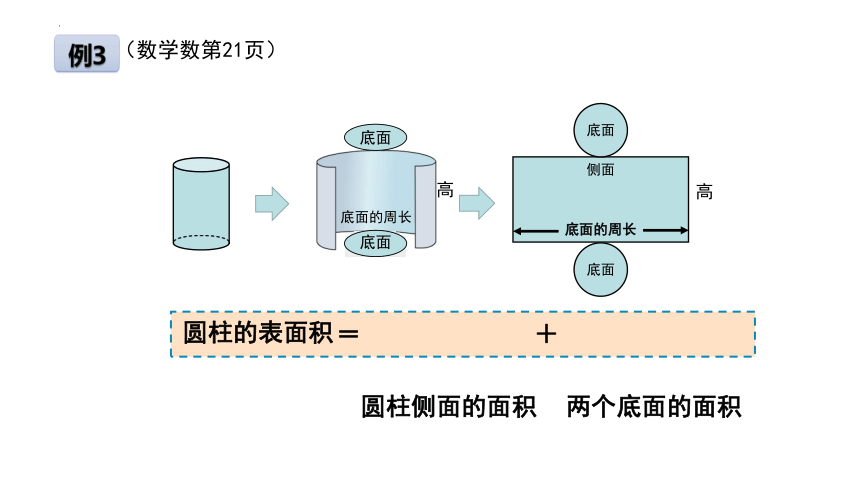
例3
(数学数第21页)
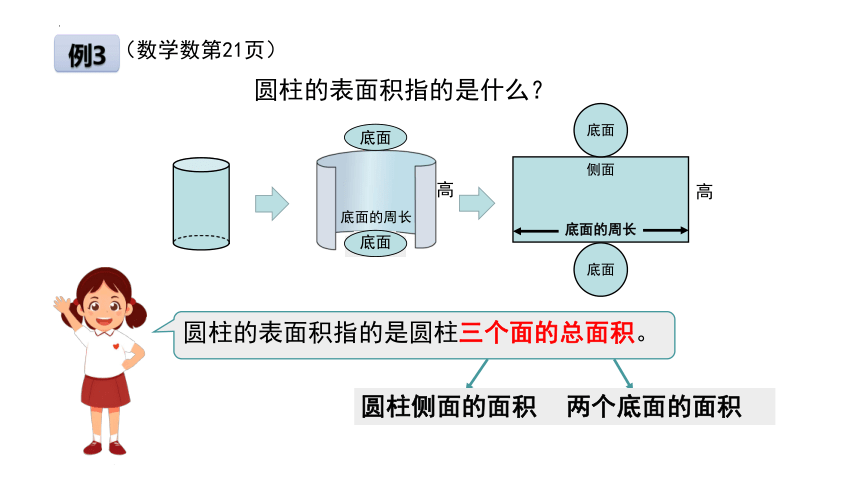
圆柱的表面积指的是什么?
圆柱的表面积指的是圆柱三个面的总面积。
底面
底面
底面
底面
底面的周长
底面的周长
高
高
侧面
圆柱侧面的面积
两个底面的面积
例3
(数学数第21页)
圆柱的表面积指的是圆柱三个面的总面积。
圆柱的表面积指的是什么?
两个底面的面积
圆柱的表面积
=
+
圆柱侧面的面积
例3
(数学数第21页)
底面
底面
底面
底面
底面的周长
底面的周长
高
高
侧面
两个底面的面积
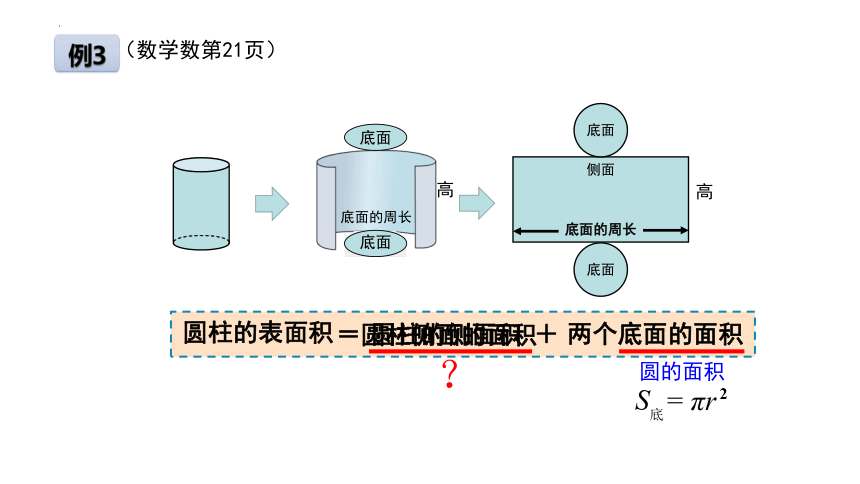
圆柱的表面积
=
圆柱侧面的面积
圆柱的侧面积
+
?
圆的面积
= πr
2
S
底
例3
(数学数第21页)
底面
底面
底面
底面
底面的周长
底面的周长
高
高
侧面
底面
底面
底面
底面
底面的周长
底面的周长
高
高
侧面
例3
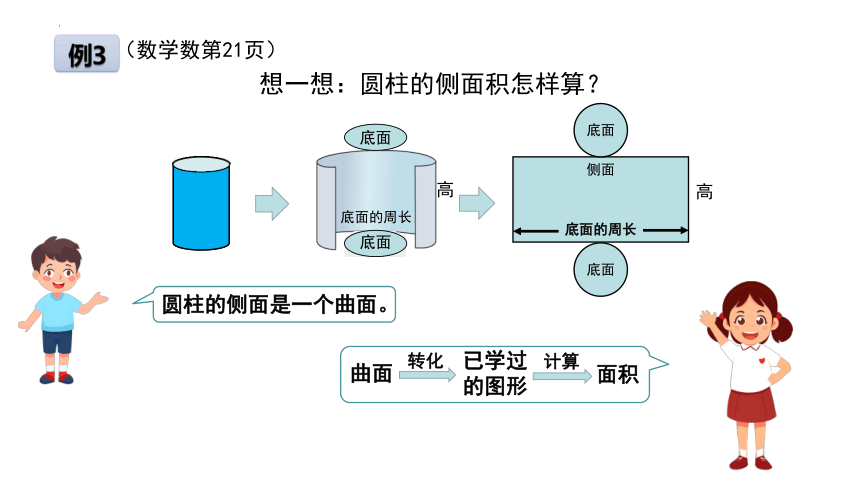
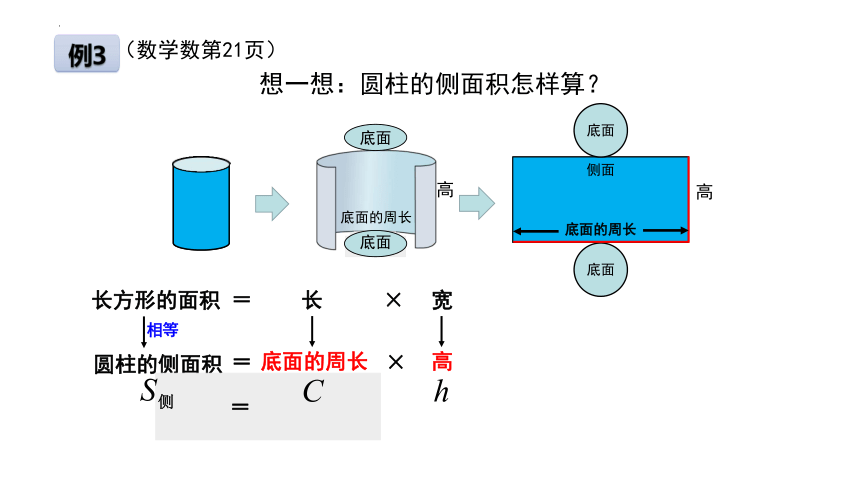
(数学数第21页)
想一想:圆柱的侧面积怎样算?
圆柱的侧面是一个曲面。
曲面
转化
已学过
的图形
面积
计算
底面
底面
底面
底面
底面的周长
底面的周长
高
高
侧面
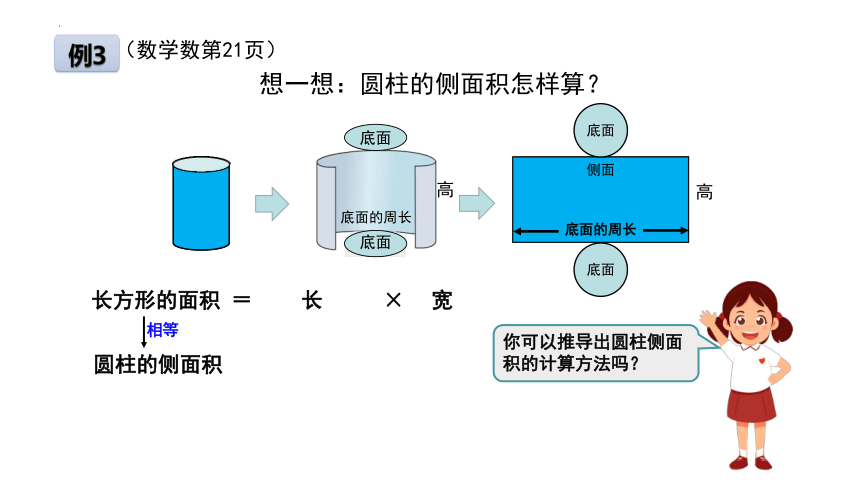
你可以推导出圆柱侧面积的计算方法吗?
长方形的面积
=
长
×
宽
圆柱的侧面积
相等
例3
(数学数第21页)
想一想:圆柱的侧面积怎样算?
底面
底面
底面
底面
底面的周长
高
侧面
长方形的面积
=
长
×
宽
圆柱的侧面积
相等
例3
(数学数第21页)
想一想:圆柱的侧面积怎样算?
底面的周长
高
=
×
=
S
侧
C
h
底面的周长
高
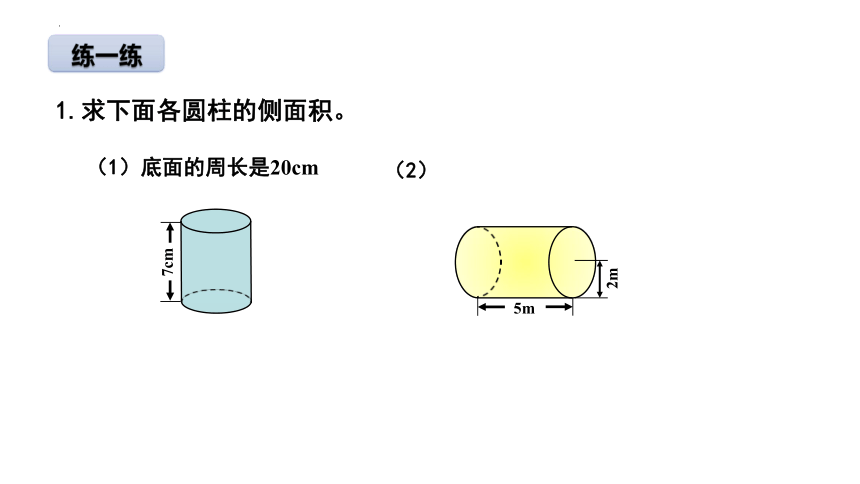
1.求下面各圆柱的侧面积。
(1)底面的周长是20cm
5m
2m
(2)
练一练
7cm
1.求下面各圆柱的侧面积。
(1)底面的周长是20cm
练一练
20cm
20×7=140(cm )
圆柱的侧面积=底面的周长×高
7cm
1.求下面各圆柱的侧面积。
(2)
练一练
圆柱的侧面积=底面的周长×高
2×3.14×2×5=62.8(m )
圆柱底面只知道半径,怎样求侧面积?
底面的周长
高
5m
2m
(1)底面的周长是20cm
1.求下面各圆柱的侧面积。
(2)
比一比
20×7=140(cm )
2×3.14×2×5=62.8(m )
底面的周长
圆柱的侧面积=底面的周长×高
5m
2m
7cm
圆柱的侧面积 =
底面的周长 × 高
圆柱的表面积 = 圆柱的侧面积 + 两个底面的面积
S
侧
C
=
h
S
表
=
+
S
底
2
S
侧
C
=
h
+ 2πr
2
底面
底面
底面
底面
底面的周长
底面的周长
高
高
侧面
例3
(数学数第21页)
圆柱的侧面积:
圆柱底面的面积:
圆柱的表面积:
2.求下面圆柱的表面积。
圆柱的表面积=圆柱的侧面积+两个底面的面积
2×3.14×2×5 = 62.8(m )
3.14×2 = 12.56(m )
62.8+12.56×2 = 87.92(m )
练一练
5m
2m
比一比
圆柱的侧面积=底面的周长×高
圆柱的表面积=圆柱的侧面积+两个底面的面积
根据题目的要求,先判断需要求圆柱哪些面的面积,再进行计算。
Ch
侧
S
= +2πr
Ch
圆柱
长方体
正方体
长方体有6个面、12条棱、8个顶点;6个面都是长方形(特殊情况下有两个相对的面是正方形);相对的4条棱的长度都相等。
正方体有6个面、12条棱、8个顶点;6个面是完全相同的正方形,它们的面积都相等;12条棱的长度都相等。
S =2(ab+ah+bh)
S =6a
V=abh
V=a
名称
图形
特征
展开图
表面积
体积
表
表
2
3
S = +2S
表
2
侧
底
S
V=Sh
V=Sh
圆柱的两个底面是完全相同的两个圆,侧面是一个曲面,两个底面之间的距离叫做圆柱的高。
(2)如果给卷成的圆柱形配两个底面,底面的周长可能是( )cm。
(1)将上面的长方形纸卷成一个圆柱形,这个圆柱的侧面积是( )cm 。
(接口处忽略不计)
10cm
5cm
50
10
1.
5cm
10cm
10cm
5cm
求这张长方形纸的面积
或5
巩固练习
高
底面的周长
巩固练习
2.某种罐头盒的形状为圆柱形,底面半径是5cm,高是20cm。要做
一个这样的罐头盒,至少用多少面积的铁皮?(接缝处忽略不计)
如果要给罐头盒的侧面贴上商标纸,这张商标纸的面积是多少?
(改编自数学书第21页“做一做”)
求圆柱的表面积
圆柱的表面积=圆柱的侧面积+两个底面的面积
2×3.14×5×20 = 628(cm )
3.14×5 = 78.5(cm )
628+78.5×2 = 785(cm )
答:至少要用785平方厘米的铁皮。
就是求这个圆柱的侧面积。
圆柱的侧面积:
圆柱底面的面积:
圆柱的表面积:
20cm
5cm
罐
头
盒
巩固练习
3.一台压路机的前轮是圆柱形,轮宽2m,直径1.2m。前轮转动
一周,压路的面积是多少平方米?
(数学书第23页第2题)
巩固练习
3.一台压路机的前轮是圆柱形,轮宽2m,直径1.2m。前轮转动
一周,压路的面积是多少平方米?
(数学书第23页第2题)
转动一周
压路的面积
圆柱的侧面积
长方形的面积
1.2m
转动一周
压路的面积
巩固练习
3.一台压路机的前轮是圆柱形,轮宽2m,直径1.2m。前轮转动
一周,压路的面积是多少平方米?
(数学书第23页第2题)
圆柱的侧面积
长方形的面积
2m
圆柱的侧面积=底面的周长×高
3.14×1.2×2=7.536(m )
答:压路的面积是7.536平方米。
底面的周长
底面的周长
轮宽
比一比
求圆柱的表面积
求圆柱的侧面积
全课总结
圆柱的表面积指的是圆柱侧面的面积和两个底面的面积之和。
1.复习数学书第21页例3。
2.完成数学书第23页第3题。
课后作业:
谢谢观看!
圆柱的表面积(一)(例3)答疑
六年级下册—人教版—数学—第三单元
7cm
圆柱的表面积=圆柱的侧面积+两个底面的面积
圆柱的侧面积=底面的周长×高
(1)
(2)
(3)
8dm
6dm
已知圆柱底面周长、高;
已知圆柱底面半径、高;
已知圆柱底面直径、高。
20cm
5m
2m
如何灵活计算圆柱的表面积?
答 疑
一根圆柱形木料高10厘米,如果沿底面直径,垂直于底面,把这根木料切成两个完全相同的半圆柱,表面积增加120平方厘米。那么原来圆柱形木料的表面积是多少平方厘米?
1.
圆柱的表面积=圆柱的侧面积+两个底面的面积
圆柱的侧面积=底面的周长×高
是哪一部分的面积?
增加了两个截面
两个完全相同的长方形
10cm
求圆柱的底面直径。
底面直径:
120÷2÷10=6(厘米)
3.14×6×10+2×3.14×(6÷2)
=188.4+56.52
=244.92(平方厘米)
答:原来圆柱形木料的表面积是244.92平方厘米。
宽:
圆柱的表面积:
10cm
5cm
5cm
一根圆柱形木料高10厘米,如果在中间把木料切成两个完全相同的小圆柱,
表面积增加56.52平方厘米。那么原来圆柱形木料的表面积是多少平方厘米?
2.
寻找与圆柱底面周长、
直径、半径的关系。
圆柱的表面积=圆柱的侧面积+两个底面的面积
圆柱的侧面积=底面的周长×高
增加了两个截面
两个与底面完全相同的圆
底面面积:
56.52÷2=28.26(平方厘米)
底面半径:
想 3.14×( )=28.26(平方厘米)
底面半径是 3 厘米。
2 × 3.14×3×10+56.52
=188.4+56.52
=244.92(平方厘米)
答:原来圆柱形木料的表面积是244.92平方厘米。
2
比一比
2
谢谢观看!
六年级下册—人教版—数学—第三单元
圆柱的表面积(一)(例3)
理解圆柱的表面积的含义。
探究并掌握圆柱侧面积及表面积的计算方法。
会计算圆柱的侧面积和表面积,并解决简单的实际问题。
学习目标
复习回顾
圆柱
长方体
正方体
长方体有6个面、12条棱、8个顶点;6个面都是长方形(特殊情况下有两个相对的面是正方形);相对的4条棱的长度都相等。
正方体有6个面、12条棱、8个顶点;6个面是完全相同的正方形,它们的面积都相等;12条棱的长度都相等。
圆柱的两个底面是完全相同的两个圆,侧面是一个曲面,两个底面之间的距离叫做圆柱的高。
S =2(ab+ah+bh)
S =6a
名称
图形
特征
展开图
表面积
体积
?
表
表
2
圆柱的表面积指的是什么?怎样计算呢?
V=abh
V=Sh
V=Sh
V=a
3
长方体或正方体 6 个面的总面积,叫做它的表面积。
复习回顾
底面
底面
底面
底面
底面的周长
底面的周长
高
高
侧面
例3
(数学数第21页)
圆柱的表面积指的是什么?
圆柱的表面积指的是圆柱三个面的总面积。
底面
底面
底面
底面
底面的周长
底面的周长
高
高
侧面
圆柱侧面的面积
两个底面的面积
例3
(数学数第21页)
圆柱的表面积指的是圆柱三个面的总面积。
圆柱的表面积指的是什么?
两个底面的面积
圆柱的表面积
=
+
圆柱侧面的面积
例3
(数学数第21页)
底面
底面
底面
底面
底面的周长
底面的周长
高
高
侧面
两个底面的面积
圆柱的表面积
=
圆柱侧面的面积
圆柱的侧面积
+
?
圆的面积
= πr
2
S
底
例3
(数学数第21页)
底面
底面
底面
底面
底面的周长
底面的周长
高
高
侧面
底面
底面
底面
底面
底面的周长
底面的周长
高
高
侧面
例3
(数学数第21页)
想一想:圆柱的侧面积怎样算?
圆柱的侧面是一个曲面。
曲面
转化
已学过
的图形
面积
计算
底面
底面
底面
底面
底面的周长
底面的周长
高
高
侧面
你可以推导出圆柱侧面积的计算方法吗?
长方形的面积
=
长
×
宽
圆柱的侧面积
相等
例3
(数学数第21页)
想一想:圆柱的侧面积怎样算?
底面
底面
底面
底面
底面的周长
高
侧面
长方形的面积
=
长
×
宽
圆柱的侧面积
相等
例3
(数学数第21页)
想一想:圆柱的侧面积怎样算?
底面的周长
高
=
×
=
S
侧
C
h
底面的周长
高
1.求下面各圆柱的侧面积。
(1)底面的周长是20cm
5m
2m
(2)
练一练
7cm
1.求下面各圆柱的侧面积。
(1)底面的周长是20cm
练一练
20cm
20×7=140(cm )
圆柱的侧面积=底面的周长×高
7cm
1.求下面各圆柱的侧面积。
(2)
练一练
圆柱的侧面积=底面的周长×高
2×3.14×2×5=62.8(m )
圆柱底面只知道半径,怎样求侧面积?
底面的周长
高
5m
2m
(1)底面的周长是20cm
1.求下面各圆柱的侧面积。
(2)
比一比
20×7=140(cm )
2×3.14×2×5=62.8(m )
底面的周长
圆柱的侧面积=底面的周长×高
5m
2m
7cm
圆柱的侧面积 =
底面的周长 × 高
圆柱的表面积 = 圆柱的侧面积 + 两个底面的面积
S
侧
C
=
h
S
表
=
+
S
底
2
S
侧
C
=
h
+ 2πr
2
底面
底面
底面
底面
底面的周长
底面的周长
高
高
侧面
例3
(数学数第21页)
圆柱的侧面积:
圆柱底面的面积:
圆柱的表面积:
2.求下面圆柱的表面积。
圆柱的表面积=圆柱的侧面积+两个底面的面积
2×3.14×2×5 = 62.8(m )
3.14×2 = 12.56(m )
62.8+12.56×2 = 87.92(m )
练一练
5m
2m
比一比
圆柱的侧面积=底面的周长×高
圆柱的表面积=圆柱的侧面积+两个底面的面积
根据题目的要求,先判断需要求圆柱哪些面的面积,再进行计算。
Ch
侧
S
= +2πr
Ch
圆柱
长方体
正方体
长方体有6个面、12条棱、8个顶点;6个面都是长方形(特殊情况下有两个相对的面是正方形);相对的4条棱的长度都相等。
正方体有6个面、12条棱、8个顶点;6个面是完全相同的正方形,它们的面积都相等;12条棱的长度都相等。
S =2(ab+ah+bh)
S =6a
V=abh
V=a
名称
图形
特征
展开图
表面积
体积
表
表
2
3
S = +2S
表
2
侧
底
S
V=Sh
V=Sh
圆柱的两个底面是完全相同的两个圆,侧面是一个曲面,两个底面之间的距离叫做圆柱的高。
(2)如果给卷成的圆柱形配两个底面,底面的周长可能是( )cm。
(1)将上面的长方形纸卷成一个圆柱形,这个圆柱的侧面积是( )cm 。
(接口处忽略不计)
10cm
5cm
50
10
1.
5cm
10cm
10cm
5cm
求这张长方形纸的面积
或5
巩固练习
高
底面的周长
巩固练习
2.某种罐头盒的形状为圆柱形,底面半径是5cm,高是20cm。要做
一个这样的罐头盒,至少用多少面积的铁皮?(接缝处忽略不计)
如果要给罐头盒的侧面贴上商标纸,这张商标纸的面积是多少?
(改编自数学书第21页“做一做”)
求圆柱的表面积
圆柱的表面积=圆柱的侧面积+两个底面的面积
2×3.14×5×20 = 628(cm )
3.14×5 = 78.5(cm )
628+78.5×2 = 785(cm )
答:至少要用785平方厘米的铁皮。
就是求这个圆柱的侧面积。
圆柱的侧面积:
圆柱底面的面积:
圆柱的表面积:
20cm
5cm
罐
头
盒
巩固练习
3.一台压路机的前轮是圆柱形,轮宽2m,直径1.2m。前轮转动
一周,压路的面积是多少平方米?
(数学书第23页第2题)
巩固练习
3.一台压路机的前轮是圆柱形,轮宽2m,直径1.2m。前轮转动
一周,压路的面积是多少平方米?
(数学书第23页第2题)
转动一周
压路的面积
圆柱的侧面积
长方形的面积
1.2m
转动一周
压路的面积
巩固练习
3.一台压路机的前轮是圆柱形,轮宽2m,直径1.2m。前轮转动
一周,压路的面积是多少平方米?
(数学书第23页第2题)
圆柱的侧面积
长方形的面积
2m
圆柱的侧面积=底面的周长×高
3.14×1.2×2=7.536(m )
答:压路的面积是7.536平方米。
底面的周长
底面的周长
轮宽
比一比
求圆柱的表面积
求圆柱的侧面积
全课总结
圆柱的表面积指的是圆柱侧面的面积和两个底面的面积之和。
1.复习数学书第21页例3。
2.完成数学书第23页第3题。
课后作业:
谢谢观看!
圆柱的表面积(一)(例3)答疑
六年级下册—人教版—数学—第三单元
7cm
圆柱的表面积=圆柱的侧面积+两个底面的面积
圆柱的侧面积=底面的周长×高
(1)
(2)
(3)
8dm
6dm
已知圆柱底面周长、高;
已知圆柱底面半径、高;
已知圆柱底面直径、高。
20cm
5m
2m
如何灵活计算圆柱的表面积?
答 疑
一根圆柱形木料高10厘米,如果沿底面直径,垂直于底面,把这根木料切成两个完全相同的半圆柱,表面积增加120平方厘米。那么原来圆柱形木料的表面积是多少平方厘米?
1.
圆柱的表面积=圆柱的侧面积+两个底面的面积
圆柱的侧面积=底面的周长×高
是哪一部分的面积?
增加了两个截面
两个完全相同的长方形
10cm
求圆柱的底面直径。
底面直径:
120÷2÷10=6(厘米)
3.14×6×10+2×3.14×(6÷2)
=188.4+56.52
=244.92(平方厘米)
答:原来圆柱形木料的表面积是244.92平方厘米。
宽:
圆柱的表面积:
10cm
5cm
5cm
一根圆柱形木料高10厘米,如果在中间把木料切成两个完全相同的小圆柱,
表面积增加56.52平方厘米。那么原来圆柱形木料的表面积是多少平方厘米?
2.
寻找与圆柱底面周长、
直径、半径的关系。
圆柱的表面积=圆柱的侧面积+两个底面的面积
圆柱的侧面积=底面的周长×高
增加了两个截面
两个与底面完全相同的圆
底面面积:
56.52÷2=28.26(平方厘米)
底面半径:
想 3.14×( )=28.26(平方厘米)
底面半径是 3 厘米。
2 × 3.14×3×10+56.52
=188.4+56.52
=244.92(平方厘米)
答:原来圆柱形木料的表面积是244.92平方厘米。
2
比一比
2
谢谢观看!
