【课件】8.2.2 两角和与差的正弦、正切 (共66张PPT)
文档属性
| 名称 | 【课件】8.2.2 两角和与差的正弦、正切 (共66张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-04 00:00:00 | ||
图片预览










文档简介
(共66张PPT)
数学-RJB-必修第三册
第八章 向量的数量积与三角恒等变换
8.2.2 两角和与差的正弦、正切
学习目标
1.会推导出两角和与差的正弦公式、正切公式.
2.会用两角和与差的正弦、余弦、正切公式进行简单的三角函数的求值、化简、证明.
3.会利用辅助角公式化asin α+bcos α为一个角的三角函数的形式.
重点:两角和与差的正弦、正切公式的应用.
难点:利用两角和的正弦公式变asin α+bcos α为一个角的三角函数的
形式.
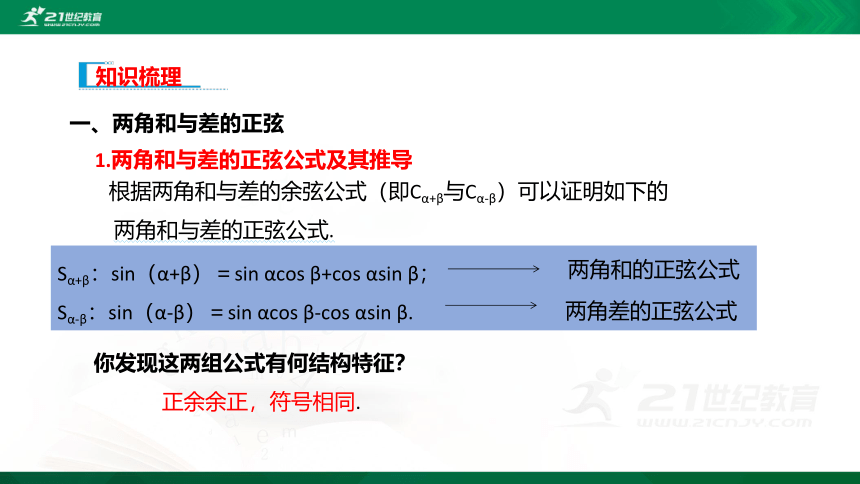
Sα+β:sin(α+β)=sin αcos β+cos αsin β;
Sα-β:sin(α-β)=sin αcos β-cos αsin β.
两角和的正弦公式
两角差的正弦公式
你发现这两组公式有何结构特征?
正余余正,符号相同.
知识梳理
一、两角和与差的正弦
1.两角和与差的正弦公式及其推导
根据两角和与差的余弦公式(即Cα+β与Cα-β)可以证明如下的
两角和与差的正弦公式.
公式的证明:
而且
sin(α-β)=sin[α+(-β)]
=sin αcos(-β)+cos αsin(-β)
=sin αcos β-cos αsin β.
2.辅助角公式
形如(且不同时为零)的式子,引入辅助角,
可变形为sin()或cos()的形式,
因此我们把sin()(或))称为辅助角公式.
其中满足:cos =,sin=.
辅助角公式实质上就是两角和与差的余弦、正弦公式的逆用.
【名师点拨】
通过辅助角公式, (且不同时为零)
可转化为sin()或cos()的形式(具体变换成哪种形式依题而定).
(且不同时为零)可转化为sin()
或cos()的形式.
由此可以很容易地解决它们的周期性、最值、单调性等有关问题.
二、两角和与差的正切公式
思考:在两角和与两角差的正弦、余弦公式的基础上,你能用tan α,tan β表示tan(α+β)和tan(α-β)吗?其中α,β应该满足什么条件?
注意:从推导的过程可以知道,α,β有一定的取值范围,即
α≠kπ+(k∈),
β≠kπ+(k∈),
α±β≠kπ+(k∈),
这样,才能保证tan α,tan β及tan(α±β)都有意义.
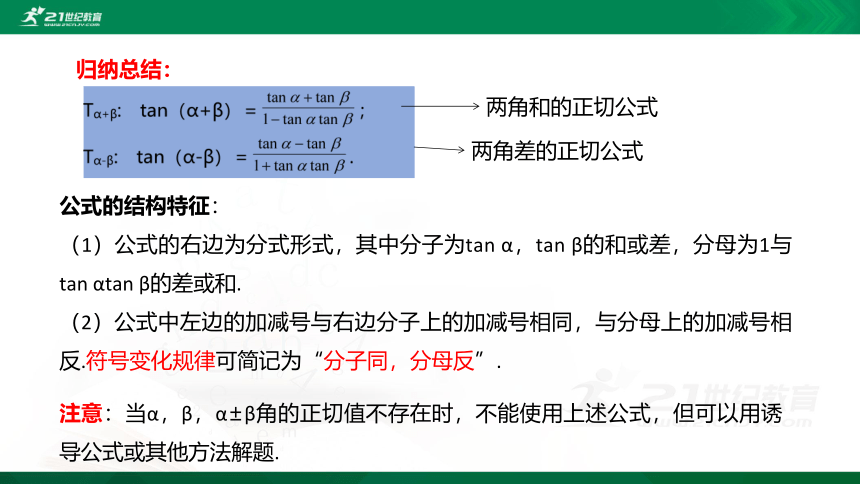
归纳总结:
两角和的正切公式
两角差的正切公式
公式的结构特征:
(1)公式的右边为分式形式,其中分子为tan α,tan β的和或差,分母为1与tan αtan β的差或和.
(2)公式中左边的加减号与右边分子上的加减号相同,与分母上的加减号相反.符号变化规律可简记为“分子同,分母反”.
注意:当α,β,α±β角的正切值不存在时,不能使用上述公式,但可以用诱导公式或其他方法解题.
想一想:对于两角和与差的正切公式,你能写出它的几种变形吗?
提示:tan αtan β,tan α±tan β,tan(α±β)三者知二求一.
常考题型
【必备知识】
1.两角和的正弦公式
sin(α+β)=sin αcos β+cos αsin β.(Sα+β)
2.两角差的正弦公式
sin(α-β)=sin αcos β-cos αsin β.(Sα-β)
A
D
解题方法
三角函数式的化简标准和要求
1.能求出值的应求出值;
2.使三角函数式的种数、项数及角的种类尽可能少;
3.使三角函数式的次数尽可能低;
4.使分母中尽量不含三角函数式和根式.
B
解题方法
用两角和与差的三角函数公式,解决“给值求值”问题的思路
创造应用公式的条件主要指构造角,要注意观察已知角与所求解析式中角的关系,将未知角用已知角表示出来,使之能直接运用公式,像这样的代换方法就是角的变换.由于和、差角与单角是相对的,因此解题过程中根据需要灵活地进行拆角或凑角的变换.
常见角的变换有:
(1)2α+β=(α+β)+α,2α-β=(α-β)+α;
(2)=-,=-;
(3)+=+(α+β),+=+(α-β).
B
A
B
2.给值求角
方法技巧
求角应当先求出角的某一个三角函数值,至于选取角的哪一个三角函数名,可参考下列原则:已知正、余弦函数值,选正弦函数或余弦函数;若角的范围是,选正弦函数或余弦函数都可以;若角的范围是,选正弦函数比余弦函数好;若角的范围是(0,π),选余弦函数比正弦函数好.
总之,最好是角的取值范围在该函数的单调区间内,这样可以使得求得的角唯一,而不需要讨论.
训练题
(3)三角形背景下的求值问题
例 [2020·黑龙江哈六中高一期末]在△ABC中,若sin(A-B)=1-2cos Asin(A+C),则△ABC的形状为 ( )
A.等边三角形 B.直角三角形
C.钝角三角形 D.无法确定
知识拓展
在三角形中,因为三个内角A+B+C=π或+=-,所以在各个角的三角函数式之间有着密切的联系,如sin(A+B)=sin C,=.可以通过某些角的三角函数值的符号,计算某个角的大小,或者判断三角形的形状等.
训练题
B
等腰三角形
4.用两角和与差的正弦公式,证明三角恒等式
例1 求证:=.
例2 已知|A|<1,且sin α=Asin(α+β),cos(α+β)≠0,
求证:tan(α+β)=.
训练题
已知sin α=msin(α+2β),且α+β≠+kπ(k∈Z),m≠1,β≠(k∈Z).
求证:tan(α+β)=·tan β.
【必备知识】
1.两角和的正切公式
tan(α+β)=.(Tα+β)
2.两角差的正切公式
tan(α-β)=.(Tα-β)
训练题
2.用两角和与差的正切公式,条件求值
(1)给值求值
例 [2019·江苏淮安高一期末]已知sin α=,α∈,cos β=-,β∈,则tan(α+β)= .
知识拓展
公式的运用要讲究一个“活”字,即注意公式的正用、逆用、变形应用等.
正用:tan(α±β)=.
逆用:=tan(α±β).
变形应用:
①tan α+tan β=tan(α+β)(1-tan αtan β);
②1-tan αtan β=;
③tan α+tan β+tan αtan βtan(α+β)=tan(α+β);
④tan αtan β=1-.
训练题
C
B
A
B
B
(3)三角形背景下的求值问题
例 [2019·贵州遵义四中高一检测]在△ABC中,tan Atan B>1,判断△ABC的形状.
知识拓展
在三角形中,因为三个内角A+B+C=π或+=-,所以在各个角的三角函数式之间有着密切的联系,如tan (A+B)=-tan C.可以通过某些角的三角函数值的符号,计算某个角的大小,或者判断三角形的形状等.
B
A
小结
2.应用公式需注意的三点
(1)要注意公式的正用、逆用,尤其是公式的逆用,要求能正确地找出所给式子与公式右边的异同,并积极创造条件逆用公式.
(2)注意拆角、拼角的技巧,将未知角用已知角表示出来,使之能直接运用公式.
3.和差角正切公式的应用,要注意变形式的应用
只要出现tan α±tan β,tan αtan β时,就要有灵活应用公式T(α±β)的意识,就不难想到解题思路.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学-RJB-必修第三册
第八章 向量的数量积与三角恒等变换
8.2.2 两角和与差的正弦、正切
学习目标
1.会推导出两角和与差的正弦公式、正切公式.
2.会用两角和与差的正弦、余弦、正切公式进行简单的三角函数的求值、化简、证明.
3.会利用辅助角公式化asin α+bcos α为一个角的三角函数的形式.
重点:两角和与差的正弦、正切公式的应用.
难点:利用两角和的正弦公式变asin α+bcos α为一个角的三角函数的
形式.
Sα+β:sin(α+β)=sin αcos β+cos αsin β;
Sα-β:sin(α-β)=sin αcos β-cos αsin β.
两角和的正弦公式
两角差的正弦公式
你发现这两组公式有何结构特征?
正余余正,符号相同.
知识梳理
一、两角和与差的正弦
1.两角和与差的正弦公式及其推导
根据两角和与差的余弦公式(即Cα+β与Cα-β)可以证明如下的
两角和与差的正弦公式.
公式的证明:
而且
sin(α-β)=sin[α+(-β)]
=sin αcos(-β)+cos αsin(-β)
=sin αcos β-cos αsin β.
2.辅助角公式
形如(且不同时为零)的式子,引入辅助角,
可变形为sin()或cos()的形式,
因此我们把sin()(或))称为辅助角公式.
其中满足:cos =,sin=.
辅助角公式实质上就是两角和与差的余弦、正弦公式的逆用.
【名师点拨】
通过辅助角公式, (且不同时为零)
可转化为sin()或cos()的形式(具体变换成哪种形式依题而定).
(且不同时为零)可转化为sin()
或cos()的形式.
由此可以很容易地解决它们的周期性、最值、单调性等有关问题.
二、两角和与差的正切公式
思考:在两角和与两角差的正弦、余弦公式的基础上,你能用tan α,tan β表示tan(α+β)和tan(α-β)吗?其中α,β应该满足什么条件?
注意:从推导的过程可以知道,α,β有一定的取值范围,即
α≠kπ+(k∈),
β≠kπ+(k∈),
α±β≠kπ+(k∈),
这样,才能保证tan α,tan β及tan(α±β)都有意义.
归纳总结:
两角和的正切公式
两角差的正切公式
公式的结构特征:
(1)公式的右边为分式形式,其中分子为tan α,tan β的和或差,分母为1与tan αtan β的差或和.
(2)公式中左边的加减号与右边分子上的加减号相同,与分母上的加减号相反.符号变化规律可简记为“分子同,分母反”.
注意:当α,β,α±β角的正切值不存在时,不能使用上述公式,但可以用诱导公式或其他方法解题.
想一想:对于两角和与差的正切公式,你能写出它的几种变形吗?
提示:tan αtan β,tan α±tan β,tan(α±β)三者知二求一.
常考题型
【必备知识】
1.两角和的正弦公式
sin(α+β)=sin αcos β+cos αsin β.(Sα+β)
2.两角差的正弦公式
sin(α-β)=sin αcos β-cos αsin β.(Sα-β)
A
D
解题方法
三角函数式的化简标准和要求
1.能求出值的应求出值;
2.使三角函数式的种数、项数及角的种类尽可能少;
3.使三角函数式的次数尽可能低;
4.使分母中尽量不含三角函数式和根式.
B
解题方法
用两角和与差的三角函数公式,解决“给值求值”问题的思路
创造应用公式的条件主要指构造角,要注意观察已知角与所求解析式中角的关系,将未知角用已知角表示出来,使之能直接运用公式,像这样的代换方法就是角的变换.由于和、差角与单角是相对的,因此解题过程中根据需要灵活地进行拆角或凑角的变换.
常见角的变换有:
(1)2α+β=(α+β)+α,2α-β=(α-β)+α;
(2)=-,=-;
(3)+=+(α+β),+=+(α-β).
B
A
B
2.给值求角
方法技巧
求角应当先求出角的某一个三角函数值,至于选取角的哪一个三角函数名,可参考下列原则:已知正、余弦函数值,选正弦函数或余弦函数;若角的范围是,选正弦函数或余弦函数都可以;若角的范围是,选正弦函数比余弦函数好;若角的范围是(0,π),选余弦函数比正弦函数好.
总之,最好是角的取值范围在该函数的单调区间内,这样可以使得求得的角唯一,而不需要讨论.
训练题
(3)三角形背景下的求值问题
例 [2020·黑龙江哈六中高一期末]在△ABC中,若sin(A-B)=1-2cos Asin(A+C),则△ABC的形状为 ( )
A.等边三角形 B.直角三角形
C.钝角三角形 D.无法确定
知识拓展
在三角形中,因为三个内角A+B+C=π或+=-,所以在各个角的三角函数式之间有着密切的联系,如sin(A+B)=sin C,=.可以通过某些角的三角函数值的符号,计算某个角的大小,或者判断三角形的形状等.
训练题
B
等腰三角形
4.用两角和与差的正弦公式,证明三角恒等式
例1 求证:=.
例2 已知|A|<1,且sin α=Asin(α+β),cos(α+β)≠0,
求证:tan(α+β)=.
训练题
已知sin α=msin(α+2β),且α+β≠+kπ(k∈Z),m≠1,β≠(k∈Z).
求证:tan(α+β)=·tan β.
【必备知识】
1.两角和的正切公式
tan(α+β)=.(Tα+β)
2.两角差的正切公式
tan(α-β)=.(Tα-β)
训练题
2.用两角和与差的正切公式,条件求值
(1)给值求值
例 [2019·江苏淮安高一期末]已知sin α=,α∈,cos β=-,β∈,则tan(α+β)= .
知识拓展
公式的运用要讲究一个“活”字,即注意公式的正用、逆用、变形应用等.
正用:tan(α±β)=.
逆用:=tan(α±β).
变形应用:
①tan α+tan β=tan(α+β)(1-tan αtan β);
②1-tan αtan β=;
③tan α+tan β+tan αtan βtan(α+β)=tan(α+β);
④tan αtan β=1-.
训练题
C
B
A
B
B
(3)三角形背景下的求值问题
例 [2019·贵州遵义四中高一检测]在△ABC中,tan Atan B>1,判断△ABC的形状.
知识拓展
在三角形中,因为三个内角A+B+C=π或+=-,所以在各个角的三角函数式之间有着密切的联系,如tan (A+B)=-tan C.可以通过某些角的三角函数值的符号,计算某个角的大小,或者判断三角形的形状等.
B
A
小结
2.应用公式需注意的三点
(1)要注意公式的正用、逆用,尤其是公式的逆用,要求能正确地找出所给式子与公式右边的异同,并积极创造条件逆用公式.
(2)注意拆角、拼角的技巧,将未知角用已知角表示出来,使之能直接运用公式.
3.和差角正切公式的应用,要注意变形式的应用
只要出现tan α±tan β,tan αtan β时,就要有灵活应用公式T(α±β)的意识,就不难想到解题思路.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
