【课件】7.3.3 余弦函数的性质与图像 数学-RJB-必修第三册
文档属性
| 名称 | 【课件】7.3.3 余弦函数的性质与图像 数学-RJB-必修第三册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-05 00:00:00 | ||
图片预览











文档简介
(共60张PPT)
数学-RJB-必修第三册
第七章 三角函数
7.3.3 余弦函数的性质与图像
学习目标
1.能正确使用“五点法”“图像变换法”作出余弦函数和的图像,并能体会正弦曲线和余弦曲线的关系.
2.理解余弦函数的性质,会求余弦函数的周期、单调区间及最值,并能利用余弦函数的图像和性质来解决相关的综合问题.
重点:余弦函数的图像和性质.
难点:余弦函数的图像和性质的综合应用.
知识梳理
一、余弦函数的定义与性质
因为对于任意一个角,都有唯一确定的余弦与之对应,所以是一个函数,一般称为余弦函数.
1.余弦函数的定义
由可知,的性质与图像和正弦型函数的相同,由此可得余弦函数的性质(如下表所示).
尝试与发现
研究余弦函数的性质,你能给出几种不同的方案呢?请你选择其中一个方案,研究余弦函数的性质.
2.余弦函数的性质
定义域
值域
最值
周期性
单调性
奇偶性
零点
当x=π+2kπ (k∈)时,ymin=-1
周期函数,最小正周期为2π
在区间[-π+2kπ,2kπ](k∈)上递增;
在区间[2kπ,π+2kπ](k∈)上递减
偶函数
()
当x=2kπ(k∈)时,ymax=1;
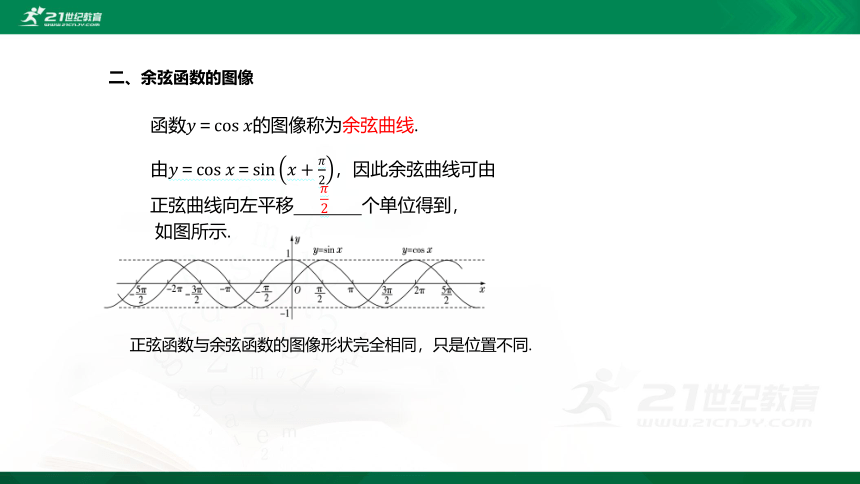
二、余弦函数的图像
函数的图像称为余弦曲线.
由,因此余弦曲线可由
正弦曲线向左平移 个单位得到,
如图所示.
正弦函数与余弦函数的图像形状完全相同,只是位置不同.
由余弦曲线可以看出,其对称轴为(k∈),对称中心为(k∈).
说明:与正弦曲线类似,余弦曲线的对称轴一定过
余弦曲线的最高点或最低点,即此时的余弦值为最
大值或最小值,余弦曲线的对称中心为余弦曲线与
轴的交点,其纵坐标.
【点拨】“五点法”画余弦函数图像
类比学习正弦函数图像的方法,观察余弦曲线,可知在函数y=cos x,x∈[0,2π]的图像上,起关键作用的五个点是它与x轴的交点和函数取得最大值、最小值的点.它们的坐标依次为
(0,1), ,(π,-1), ,(2π,1),
用光滑曲线顺次将它们连接起来就可得到函数y=cos x,x∈[0,2π]的简图.
常考题型
一、余弦函数的性质——定义域、值域、最值
1.利用余弦函数的值域求参数
例1 若cos x=2m-1,且x∈R,则m的取值范围是 ( )
A.(-∞,1] B.[0,+∞)
C.[-1,0] D.[0,1]
【解析】∵ ,
,即,解得,
故的取值范围是[0,1].
【答案】D
【解题提示】(1)(2)利用整体代换法;(3)利用二次函数的性质求解;(4)先分离常数或反解出cos x,再利用-1≤cos x≤1求解.
◆利用余弦函数的性质,求复合函数的最值、值域问题的方法
1.对于y=acos x+b的形式,借助余弦函数的有界性|cos x|≤1求解.
2.对于y=Acos (ωx+φ)+k(Aω≠0)的形式,采用整体代换法
求解,令ωx+φ=t,借助y=cos t的图像及性质求解,注意x的
取值范围对t的取值范围的影响.
3.对于y=的形式,采用分离常数法或反解出cos x,再利
用余弦函数的有界性求解.
4.对于y=acos2x+bcos x+c的形式,利用二次函数的有关知识求解.
二、余弦函数的性质——周期性
1.判断余弦型函数是否为周期函数
例3 判断函数y=,x∈[-π,π]是不是周期函数.若不是,请说明理由,并指出在什么条件下该函数是周期函数.
【解题提示】要判断一个函数为周期函数,一要看定义域,即对任意,有;二是对任意,有.要说明一个函数不是周期函数或者不是以为周期的函数,只要举一反例即可.
【解】∵ x=π时,x+T[-π,π],不符合周期函数的定义,
∴ y=,x∈[-π,π]不是周期函数.
要使函数为周期函数,需将条件x∈[-π,π]改为x∈R.
∵ 当x∈R时,有
y===,
∴ y=是以π为周期的周期函数.
2、求余弦型函数的周期
例4 求下列函数的最小正周期:y=cos 2x.
解:令u=2x,则y=cos 2x=cos u是周期函数,且最小正周期为2π,
∴ cos(u+2π)=cos u,
即cos(2x+2π)=cos[2(x+π)]=cos 2x.
∴ y=cos 2x的最小正周期为π.
◆求余弦型函数周期的方法
1.定义法:对于定义域内每一个x是否存在非零常数T,使f(x+T)=f(x),若存在,则T是它的一个周期.
2.公式法:形如y=Acos (ωx+φ)(其中A,ω,φ为
常数,且A≠0,ω≠0)的函数的周期T=.
三、余弦函数的性质——奇偶性
例5 判断下列函数的奇偶性:
(1)f(x)=sin xcos x;
(2)f(x)=;
(3)f(x)=.
【解】(1)函数的定义域为,关于原点对称.
∵ f(-x)=sin(-x)cos(-x)=-sin xcos x=-f(x),
∴ f(x)=sin xcos x为奇函数.
(2)函数应满足1-sin x≠0,
∴ 函数的定义域为,显然定义域不
关于原点对称,
∴ f(x)=为非奇非偶函数.
(3)由得cos x=1,
∴ 函数的定义域为{x|x=2kπ,k∈Z},定义域关于原点对称.
当cos x=1时,f(x)=0,f(x)=±f(-x).
∴ f(x)=既是奇函数又是偶函数.
◆函数奇偶性的判断方法
判断三角函数的奇偶性,首先要观察定义域是否关于原点对称,在定义域关于原点对称的前提下,再根据
f(-x)与f(x)的关系确定奇偶性.函数解析式能化简的要化简,必须进行恒等变形.
四、余弦函数的性质——单调性
1.利用余弦函数的单调性,比较余弦值的大小
◆利用单调性比较大小的方法
单调性是对一个函数的某个区间而言的,一般按如下情况进行比较:
1.比较同名的三角函数值的大小,将所给的角运用诱导公式转化到同一单调区间,在同一单调区间上运用单调性比较大小,若比较复杂,先化简;
2.比较不同名的三角函数值的大小,应先化为同名的三角函数值,再进行比较.
A
2.利用余弦函数的单调性,求复合函数的单调区间
【解析】(1)∵ -<0,
∴ y=1-cos x的单调性与y=cos x的单调性相反.
∵ y=cos x的单调增区间是[2kπ-π,2kπ](k∈),
∴ y=1-cos x的单调减区间是[2kπ-π,2kπ](k∈Z).
取k=0得D.
【答案】 (1)D (2)A
◆利用余弦函数的单调性,求复合函数的单调区间的方法
1.形如y=acos x+b(a≠0)的函数的单调区间
当a>0时,其单调性同y=cos x的单调性一致;
当a<0时,其单调性同y=cos x的单调性恰好相反.
2.形如y=Acos (ωx+φ)(ω>0)的函数的单调区间
当A>0时,由2kπ≤ωx+φ≤π+2kπ(k∈Z),解得函数的减区间;
由-π+2kπ≤ωx+φ≤2kπ(k∈Z),解得函数的增区间.
当A<0时,由2kπ≤ωx+φ≤π+2kπ(k∈Z),解得函数的增区间;
由-π+2kπ ≤ωx +φ≤2kπ(k∈Z),解得函数的减区间.
若ω<0,则先利用诱导公式化为ω>0的情形.
3.复合函数的单调性
按照同增异减进行求解.和对数有关的函数,因为要保证真数大于零,所以必须先求函数的定义域.
解:由题意得2kπ<2x<2kπ+,k∈,
∴ kπ∴ y=(cos 2x)的增区间为,k∈.
3.已知复合函数的单调性,利用余弦函数的单调性,求参数
训练题
已知f(x)=-8cos在区间上是单调函数,则实数的最大值为 .
五、余弦函数的图像
1.五点法作与余弦函数相关的复合函数的图像
例8 用“五点法”作函数y=2cos x+1,x∈[0,2π]的简图.
【解】∵ x∈[0,2π],∴ 令x=0,,π,,2π.
列表:
x 0 π 2π
cos x 1 0 -1 0 1
y 3 1 -1 1 3
描点,连线,得函数y=2cos x+1,x∈[0,2π]的简图,如图所示.
【点拨】由y=cos x的图像得到y=Acos(ωx+φ)的图像时,规律与方法可类比正弦函数,应先令ωx+φ取0,,π,,2π等(k∈Z)类型的值,反解出x的值后再列表、描点、作图.
训练题
作函数y=cos x-1,x∈[0,2π]的简图.
解:按五个关键点列表:
x 0 π 2π
cos x-1 - -1 - -1 -
描点,连线,得函数y=cos x-1,x∈[0,2π]的简图,如图所示.
2.余弦函数的图像变换
【答案】C
训练题
[浙江卷]把函数y=cos 2x+1的图像上所有点的横坐标
伸长到原来的2倍(纵坐标不变),然后向左平移1个单
位长度,再向下平移1个单位长度,得到的图像是 ( )
A B
C D
A
六、余弦函数的对称性
例10 函数y=的图像与函数y=的图像 ( )
A.有相同的对称轴但无相同的对称中心
B.有相同的对称中心但无相同的对称轴
C.既有相同的对称轴也有相同的对称中心
D.既无相同的对称中心也无相同的对称轴
【解析】由2x-=k1π+,k1∈Z,可得函数y=的图像的对称轴为直线x=+,k1∈Z.
由x-=k2π,k2∈Z,可得函数y=的图像的对称轴为直线x=k2π+,k2∈Z.
当k1=k2=0时,二者有相同的对称轴.
由2x-=k3π,k3∈Z,可得函数y=的图像的对称中心为点,k3∈Z.
由x-=k4π+,k4∈Z,可得函数y=的图像的对称中心为点,k4∈Z.
设+=k4π+,k3,k4∈Z,解得k3=2k4+,与k3,k4∈Z矛盾.
故两个函数的图像没有相同的对称中心.故选A.
【答案】 A
【解题技法】
若求函数y=Acos(ωx+φ)(Aω≠0)的图像的对称中心或对称轴,应将ωx+φ看成一个整体,利用整体代入思想,令ωx+φ等于kπ+或kπ(k∈Z),解出的x的值即对称中心的横坐标(纵坐标为零)或对称轴与x轴的交点的横坐标.
小结
1.余弦函数的图像
图像常用作法:平移法、“五点法”
2.余弦函数的性质
函数 性质 y=cos x
定义域
值域 余弦曲线夹在两条平行线y=1和y=-1之间,故值域是[-1,1]
最值 当x=2kπ(k∈)时,ymax=1;
当x=(2k+1)π(k∈)时,ymin=-1
周期性 周期函数,最小正周期为2π
单调性 在每一个区间[(2k-1)π,2kπ](k∈)上是增加的;
在每一个区间[2kπ,(2k+1)π](k∈)上是减少的
奇偶性 偶函数,图像关于y轴对称
图像的对称性 对称轴为直线x=kπ(k∈),对称中心为点(k∈)
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学-RJB-必修第三册
第七章 三角函数
7.3.3 余弦函数的性质与图像
学习目标
1.能正确使用“五点法”“图像变换法”作出余弦函数和的图像,并能体会正弦曲线和余弦曲线的关系.
2.理解余弦函数的性质,会求余弦函数的周期、单调区间及最值,并能利用余弦函数的图像和性质来解决相关的综合问题.
重点:余弦函数的图像和性质.
难点:余弦函数的图像和性质的综合应用.
知识梳理
一、余弦函数的定义与性质
因为对于任意一个角,都有唯一确定的余弦与之对应,所以是一个函数,一般称为余弦函数.
1.余弦函数的定义
由可知,的性质与图像和正弦型函数的相同,由此可得余弦函数的性质(如下表所示).
尝试与发现
研究余弦函数的性质,你能给出几种不同的方案呢?请你选择其中一个方案,研究余弦函数的性质.
2.余弦函数的性质
定义域
值域
最值
周期性
单调性
奇偶性
零点
当x=π+2kπ (k∈)时,ymin=-1
周期函数,最小正周期为2π
在区间[-π+2kπ,2kπ](k∈)上递增;
在区间[2kπ,π+2kπ](k∈)上递减
偶函数
()
当x=2kπ(k∈)时,ymax=1;
二、余弦函数的图像
函数的图像称为余弦曲线.
由,因此余弦曲线可由
正弦曲线向左平移 个单位得到,
如图所示.
正弦函数与余弦函数的图像形状完全相同,只是位置不同.
由余弦曲线可以看出,其对称轴为(k∈),对称中心为(k∈).
说明:与正弦曲线类似,余弦曲线的对称轴一定过
余弦曲线的最高点或最低点,即此时的余弦值为最
大值或最小值,余弦曲线的对称中心为余弦曲线与
轴的交点,其纵坐标.
【点拨】“五点法”画余弦函数图像
类比学习正弦函数图像的方法,观察余弦曲线,可知在函数y=cos x,x∈[0,2π]的图像上,起关键作用的五个点是它与x轴的交点和函数取得最大值、最小值的点.它们的坐标依次为
(0,1), ,(π,-1), ,(2π,1),
用光滑曲线顺次将它们连接起来就可得到函数y=cos x,x∈[0,2π]的简图.
常考题型
一、余弦函数的性质——定义域、值域、最值
1.利用余弦函数的值域求参数
例1 若cos x=2m-1,且x∈R,则m的取值范围是 ( )
A.(-∞,1] B.[0,+∞)
C.[-1,0] D.[0,1]
【解析】∵ ,
,即,解得,
故的取值范围是[0,1].
【答案】D
【解题提示】(1)(2)利用整体代换法;(3)利用二次函数的性质求解;(4)先分离常数或反解出cos x,再利用-1≤cos x≤1求解.
◆利用余弦函数的性质,求复合函数的最值、值域问题的方法
1.对于y=acos x+b的形式,借助余弦函数的有界性|cos x|≤1求解.
2.对于y=Acos (ωx+φ)+k(Aω≠0)的形式,采用整体代换法
求解,令ωx+φ=t,借助y=cos t的图像及性质求解,注意x的
取值范围对t的取值范围的影响.
3.对于y=的形式,采用分离常数法或反解出cos x,再利
用余弦函数的有界性求解.
4.对于y=acos2x+bcos x+c的形式,利用二次函数的有关知识求解.
二、余弦函数的性质——周期性
1.判断余弦型函数是否为周期函数
例3 判断函数y=,x∈[-π,π]是不是周期函数.若不是,请说明理由,并指出在什么条件下该函数是周期函数.
【解题提示】要判断一个函数为周期函数,一要看定义域,即对任意,有;二是对任意,有.要说明一个函数不是周期函数或者不是以为周期的函数,只要举一反例即可.
【解】∵ x=π时,x+T[-π,π],不符合周期函数的定义,
∴ y=,x∈[-π,π]不是周期函数.
要使函数为周期函数,需将条件x∈[-π,π]改为x∈R.
∵ 当x∈R时,有
y===,
∴ y=是以π为周期的周期函数.
2、求余弦型函数的周期
例4 求下列函数的最小正周期:y=cos 2x.
解:令u=2x,则y=cos 2x=cos u是周期函数,且最小正周期为2π,
∴ cos(u+2π)=cos u,
即cos(2x+2π)=cos[2(x+π)]=cos 2x.
∴ y=cos 2x的最小正周期为π.
◆求余弦型函数周期的方法
1.定义法:对于定义域内每一个x是否存在非零常数T,使f(x+T)=f(x),若存在,则T是它的一个周期.
2.公式法:形如y=Acos (ωx+φ)(其中A,ω,φ为
常数,且A≠0,ω≠0)的函数的周期T=.
三、余弦函数的性质——奇偶性
例5 判断下列函数的奇偶性:
(1)f(x)=sin xcos x;
(2)f(x)=;
(3)f(x)=.
【解】(1)函数的定义域为,关于原点对称.
∵ f(-x)=sin(-x)cos(-x)=-sin xcos x=-f(x),
∴ f(x)=sin xcos x为奇函数.
(2)函数应满足1-sin x≠0,
∴ 函数的定义域为,显然定义域不
关于原点对称,
∴ f(x)=为非奇非偶函数.
(3)由得cos x=1,
∴ 函数的定义域为{x|x=2kπ,k∈Z},定义域关于原点对称.
当cos x=1时,f(x)=0,f(x)=±f(-x).
∴ f(x)=既是奇函数又是偶函数.
◆函数奇偶性的判断方法
判断三角函数的奇偶性,首先要观察定义域是否关于原点对称,在定义域关于原点对称的前提下,再根据
f(-x)与f(x)的关系确定奇偶性.函数解析式能化简的要化简,必须进行恒等变形.
四、余弦函数的性质——单调性
1.利用余弦函数的单调性,比较余弦值的大小
◆利用单调性比较大小的方法
单调性是对一个函数的某个区间而言的,一般按如下情况进行比较:
1.比较同名的三角函数值的大小,将所给的角运用诱导公式转化到同一单调区间,在同一单调区间上运用单调性比较大小,若比较复杂,先化简;
2.比较不同名的三角函数值的大小,应先化为同名的三角函数值,再进行比较.
A
2.利用余弦函数的单调性,求复合函数的单调区间
【解析】(1)∵ -<0,
∴ y=1-cos x的单调性与y=cos x的单调性相反.
∵ y=cos x的单调增区间是[2kπ-π,2kπ](k∈),
∴ y=1-cos x的单调减区间是[2kπ-π,2kπ](k∈Z).
取k=0得D.
【答案】 (1)D (2)A
◆利用余弦函数的单调性,求复合函数的单调区间的方法
1.形如y=acos x+b(a≠0)的函数的单调区间
当a>0时,其单调性同y=cos x的单调性一致;
当a<0时,其单调性同y=cos x的单调性恰好相反.
2.形如y=Acos (ωx+φ)(ω>0)的函数的单调区间
当A>0时,由2kπ≤ωx+φ≤π+2kπ(k∈Z),解得函数的减区间;
由-π+2kπ≤ωx+φ≤2kπ(k∈Z),解得函数的增区间.
当A<0时,由2kπ≤ωx+φ≤π+2kπ(k∈Z),解得函数的增区间;
由-π+2kπ ≤ωx +φ≤2kπ(k∈Z),解得函数的减区间.
若ω<0,则先利用诱导公式化为ω>0的情形.
3.复合函数的单调性
按照同增异减进行求解.和对数有关的函数,因为要保证真数大于零,所以必须先求函数的定义域.
解:由题意得2kπ<2x<2kπ+,k∈,
∴ kπ
3.已知复合函数的单调性,利用余弦函数的单调性,求参数
训练题
已知f(x)=-8cos在区间上是单调函数,则实数的最大值为 .
五、余弦函数的图像
1.五点法作与余弦函数相关的复合函数的图像
例8 用“五点法”作函数y=2cos x+1,x∈[0,2π]的简图.
【解】∵ x∈[0,2π],∴ 令x=0,,π,,2π.
列表:
x 0 π 2π
cos x 1 0 -1 0 1
y 3 1 -1 1 3
描点,连线,得函数y=2cos x+1,x∈[0,2π]的简图,如图所示.
【点拨】由y=cos x的图像得到y=Acos(ωx+φ)的图像时,规律与方法可类比正弦函数,应先令ωx+φ取0,,π,,2π等(k∈Z)类型的值,反解出x的值后再列表、描点、作图.
训练题
作函数y=cos x-1,x∈[0,2π]的简图.
解:按五个关键点列表:
x 0 π 2π
cos x-1 - -1 - -1 -
描点,连线,得函数y=cos x-1,x∈[0,2π]的简图,如图所示.
2.余弦函数的图像变换
【答案】C
训练题
[浙江卷]把函数y=cos 2x+1的图像上所有点的横坐标
伸长到原来的2倍(纵坐标不变),然后向左平移1个单
位长度,再向下平移1个单位长度,得到的图像是 ( )
A B
C D
A
六、余弦函数的对称性
例10 函数y=的图像与函数y=的图像 ( )
A.有相同的对称轴但无相同的对称中心
B.有相同的对称中心但无相同的对称轴
C.既有相同的对称轴也有相同的对称中心
D.既无相同的对称中心也无相同的对称轴
【解析】由2x-=k1π+,k1∈Z,可得函数y=的图像的对称轴为直线x=+,k1∈Z.
由x-=k2π,k2∈Z,可得函数y=的图像的对称轴为直线x=k2π+,k2∈Z.
当k1=k2=0时,二者有相同的对称轴.
由2x-=k3π,k3∈Z,可得函数y=的图像的对称中心为点,k3∈Z.
由x-=k4π+,k4∈Z,可得函数y=的图像的对称中心为点,k4∈Z.
设+=k4π+,k3,k4∈Z,解得k3=2k4+,与k3,k4∈Z矛盾.
故两个函数的图像没有相同的对称中心.故选A.
【答案】 A
【解题技法】
若求函数y=Acos(ωx+φ)(Aω≠0)的图像的对称中心或对称轴,应将ωx+φ看成一个整体,利用整体代入思想,令ωx+φ等于kπ+或kπ(k∈Z),解出的x的值即对称中心的横坐标(纵坐标为零)或对称轴与x轴的交点的横坐标.
小结
1.余弦函数的图像
图像常用作法:平移法、“五点法”
2.余弦函数的性质
函数 性质 y=cos x
定义域
值域 余弦曲线夹在两条平行线y=1和y=-1之间,故值域是[-1,1]
最值 当x=2kπ(k∈)时,ymax=1;
当x=(2k+1)π(k∈)时,ymin=-1
周期性 周期函数,最小正周期为2π
单调性 在每一个区间[(2k-1)π,2kπ](k∈)上是增加的;
在每一个区间[2kπ,(2k+1)π](k∈)上是减少的
奇偶性 偶函数,图像关于y轴对称
图像的对称性 对称轴为直线x=kπ(k∈),对称中心为点(k∈)
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
