苏科版九年级下册 6.1多边形与平行四边形 课件(19张)
文档属性
| 名称 | 苏科版九年级下册 6.1多边形与平行四边形 课件(19张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 442.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-05 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
6.1多边形与平行四边形
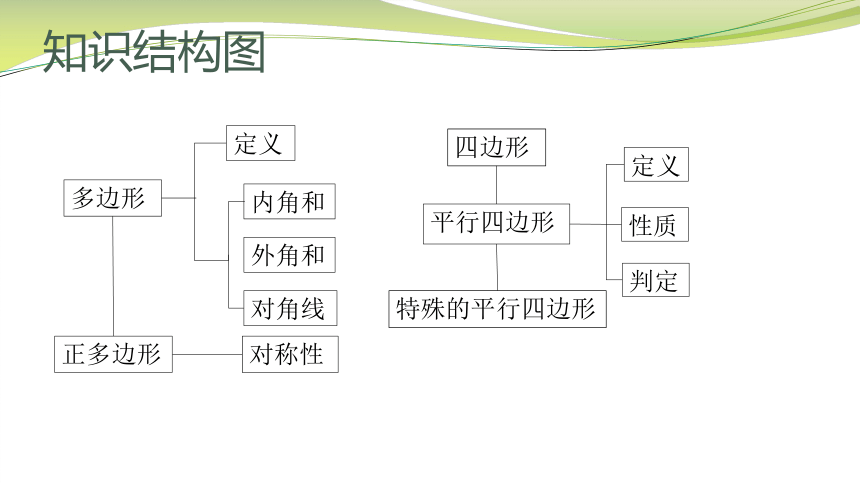
知识结构图
多边形
定义
内角和
外角和
对角线
正多边形
对称性
平行四边形
定义
性质
判定
四边形
特殊的平行四边形
知识清单
1.多边形及其相关概念
在平面内,n条不共线的线段,首尾依次相连所组成的图形叫做n边形.
n边形 (n≥3) 内角和 n边形的内角和为(n-2) 180°
外角和 n边形的外角和为360°
对角线 过n(n>3)边形一个顶点可引(n-3)条对角线,n边形共有 条对角线
知识清单
2.正多边形及其相关概念
正n边形 (n≥3) 定义 各个角都相等,各条边都相等的n边形
内角、外角 n边形的每个内角 或 ;
每个外角 .
对称性 正n边形都是轴对称图形,有n条对称轴;
边数为偶数的正n边形还是中心对称图形.
知识清单
3.平行四边形概念、性质
平行四边形:两组对边分别平行的四边形 边 对边平行且相等 AB∥CD,AD∥BC;
AB=CD,AD=BC.
角 对角相等 ∠DAB=∠DCB,
∠ADC=∠ABC;
对角线 对角线互相平分 AO=CO,BO=DO
对称性 是中心对称图形, 对称中心是对角线的交点
面积 S=底×高
B
A
C
D
O
E
知识清单
(2)同底等高的平行四边形的面积相等.
(1)平行四边形的两条对角线将平行四边形分成面积相等的四个三角形.
(3)若一条直线过平行四边形的对角线的交点,则这条直线等分平行四边形的面积.
与面积有关的几个重要结论:
知识清单
4.平行四边形的判定
边 两组对边分别平行的四边形 是平行四边形 ∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
两组对边分别相等的四边形 是平行四边形 ∵ AB=CD,AD=BC
∴四边形ABCD是平行四边形
一组对边平行且相等的四边形 是平行四边形 ∵ AB∥CD,AB=CD
∴四边形ABCD是平行四边形
对角线 对角线互相平分的四边形 是平行四边形 ∵AO=CO,BO=DO
∴四边形ABCD是平行四边形
B
A
C
D
O
E
D. ∠ABD=∠ADB
热身小练
B
C
A
A
热身小练
72°
A
B
C
D
E
A
B
C
D
E
角平分线
∠1=∠2
1
2
3
∠2=∠3
1
2
3
平行线
等腰三角形
∠2=∠3
AB=BE=6
28或20
6
6
2
6
6
2
典型例题
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
1
∴∠D=∠1.
∵E是DC中点,
∴DE=EC.
在△ADE和△FCE中
∴△ADE≌△FCE
∴AD=FC
又AD=BC
∴BC=FC
(2)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴△ABG∽△CEG
∴ ,
∵CD=2EC,
∴AB=2EC.
∴ ,
∵△GEC的面积是2,
∴S△BGC=2S△GEC=4
∴S△ABG=4S△GEC=8
∴S△ABC=S△BGC+ S△ABG =12
∴S□ABCD=2S△ABC=24
典型例题
(1)利用平行四边形的性质,即可判定 ,即可得到AE=CD,再根据CD∥AE,即可证得四边形ACDE是平行四边形;
(2)利用(1)的结论和平行四边形的性质可得AC=CD,由此即可判定是菱形.
(1)证明:在□ABCD中,AB∥CD,
∴∠EAO=∠CDO
∵点O为AD的中点,∴AO=DO
∴AE=CD
又∵BE∥CD ,
∴四边形ACDE是平行四边形
在△AOE与△DOC中
∴
(2)解:∵四边形ABCD是平行四边形,
∴AB=CD
又AB=AC,
∴AC=CD
∴□ACDE是菱形.
典型例题
例2.如图,在四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为点
E,F.
(1)请你只添加一个条件(不另加辅助线),使得四边形AECF 为平行四边形.你添加的条件是________;
(2)添加了条件后,证明四边形AECF为平行四边形.
(1)由题意可知AE∥CF,要使得四边形AECF为平行四边形,则使得AF∥CE即可,从而添加适当条件即可;
(2)根据(1)的思路,利用平行四边形的定义证明即可.
(1)显然,直接添加AF∥CE,可根据定义得到结果,
(2)证明:∵ AE⊥BD,CF⊥BD,
∴AE∥CF
∵AF∥CE
∴四边形AECF为平行四边形.
AF∥CE
典型例题
若选②,即OE=OF;根据平行四边形的性质可得BO=DO,然后即可证明四边形BEDF是平行四边形,进而可得结论;若选①,即AE=CF;根据平行四边形的性质得出OE=OF后,同上面的思路解答即可;若选③,即BE∥DF,则∠BEO=∠DFO,再根据平行四边形的性质可证△BOE≌△DOF,于是可得结论.
解:若选②,即OE=OF;
证明:∵四边形ABCD是平行四边形,
∴BO=DO,
∵OE=OF,
∴四边形BEDF是平行四边形,∴BE=DF;
若选①,即AE=CF;
证明:∵四边形ABCD是平行四边形,
∴BO=DO,AO=CO,
∵AE=CF,∴OE=OF,
∴四边形BEDF是平行四边形
∴BE=DF;
若选③,即BE∥DF;
证明:∵四边形ABCD是平行四边形,
∴BO=DO,
∵BE∥DF;
∴∠BEO=∠DFO,
又∠BOE=∠DOF,
∴△BOE≌△DOF(AAS),
∴BE=DF;
拓展提高
(1)①利用平行四边形的性质和角平分线的定义先分别求出DE=AD=5,BC=CF=5,即可完成求解.
②证明出EF=CD即可完成求解.
拓展提高
(1)①利用平行四边形的性质和角平分线的定义先分别求出DE=AD=5,BC=CF=5,即可完成求解.
(1)①如图1,四边形ABCD是平行四边形,
∴AB∥CD, ∴∠DEA=∠EAB,
∵AE平分∠DAB ∴∠DAE=∠EAB
∴∠DAE=∠DEA ∴DE=AD=5
同理可得:BC=CF=5
∵点E与点F重合 ∴AB=CD=10
拓展提高
②证明出EF=CD即可完成求解.
②如图2,点E与点C重合,
同理可证DE=DC=AD=5
∴□ABCD是菱形
∵CF=BC=5
∴点F与点D重合
∴EF=DC=5
拓展提高
(2)本小题由于E、F点的位置不确定,故应先分情况讨论,再根据每种情况,利用DE=AD,CF=CB以及点 C,D,E,F相邻两点间的距离相等建立相等关系求解即可.
拓展提高
(2)本小题由于E、F点的位置不确定,故应先分情况讨论,再根据每种情况,利用DE=AD,CF=CB以及点 C,D,E,F相邻两点间的距离相等建立相等关系求解即可.
如图,在□ABCD中,∠DAB,∠ABC的平分线AE,BF分别与直线CD交于点E,F,当点C,D,E,F相邻两点间的距离相等时,求 的值.
(2)情况1,如图3,
可得AD=DE=EF=FC,
∴
情况2,如图4,
同理可得,AD=DE,BC=CF
又∵DF=FE=CE
∴
情况3,如图5,
由上,同理可得,AD=DE,BC=CF
又∵FD=DC=CE
∴
综上: 的值 或 或2.
谢 谢
6.1多边形与平行四边形
知识结构图
多边形
定义
内角和
外角和
对角线
正多边形
对称性
平行四边形
定义
性质
判定
四边形
特殊的平行四边形
知识清单
1.多边形及其相关概念
在平面内,n条不共线的线段,首尾依次相连所组成的图形叫做n边形.
n边形 (n≥3) 内角和 n边形的内角和为(n-2) 180°
外角和 n边形的外角和为360°
对角线 过n(n>3)边形一个顶点可引(n-3)条对角线,n边形共有 条对角线
知识清单
2.正多边形及其相关概念
正n边形 (n≥3) 定义 各个角都相等,各条边都相等的n边形
内角、外角 n边形的每个内角 或 ;
每个外角 .
对称性 正n边形都是轴对称图形,有n条对称轴;
边数为偶数的正n边形还是中心对称图形.
知识清单
3.平行四边形概念、性质
平行四边形:两组对边分别平行的四边形 边 对边平行且相等 AB∥CD,AD∥BC;
AB=CD,AD=BC.
角 对角相等 ∠DAB=∠DCB,
∠ADC=∠ABC;
对角线 对角线互相平分 AO=CO,BO=DO
对称性 是中心对称图形, 对称中心是对角线的交点
面积 S=底×高
B
A
C
D
O
E
知识清单
(2)同底等高的平行四边形的面积相等.
(1)平行四边形的两条对角线将平行四边形分成面积相等的四个三角形.
(3)若一条直线过平行四边形的对角线的交点,则这条直线等分平行四边形的面积.
与面积有关的几个重要结论:
知识清单
4.平行四边形的判定
边 两组对边分别平行的四边形 是平行四边形 ∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
两组对边分别相等的四边形 是平行四边形 ∵ AB=CD,AD=BC
∴四边形ABCD是平行四边形
一组对边平行且相等的四边形 是平行四边形 ∵ AB∥CD,AB=CD
∴四边形ABCD是平行四边形
对角线 对角线互相平分的四边形 是平行四边形 ∵AO=CO,BO=DO
∴四边形ABCD是平行四边形
B
A
C
D
O
E
D. ∠ABD=∠ADB
热身小练
B
C
A
A
热身小练
72°
A
B
C
D
E
A
B
C
D
E
角平分线
∠1=∠2
1
2
3
∠2=∠3
1
2
3
平行线
等腰三角形
∠2=∠3
AB=BE=6
28或20
6
6
2
6
6
2
典型例题
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
1
∴∠D=∠1.
∵E是DC中点,
∴DE=EC.
在△ADE和△FCE中
∴△ADE≌△FCE
∴AD=FC
又AD=BC
∴BC=FC
(2)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴△ABG∽△CEG
∴ ,
∵CD=2EC,
∴AB=2EC.
∴ ,
∵△GEC的面积是2,
∴S△BGC=2S△GEC=4
∴S△ABG=4S△GEC=8
∴S△ABC=S△BGC+ S△ABG =12
∴S□ABCD=2S△ABC=24
典型例题
(1)利用平行四边形的性质,即可判定 ,即可得到AE=CD,再根据CD∥AE,即可证得四边形ACDE是平行四边形;
(2)利用(1)的结论和平行四边形的性质可得AC=CD,由此即可判定是菱形.
(1)证明:在□ABCD中,AB∥CD,
∴∠EAO=∠CDO
∵点O为AD的中点,∴AO=DO
∴AE=CD
又∵BE∥CD ,
∴四边形ACDE是平行四边形
在△AOE与△DOC中
∴
(2)解:∵四边形ABCD是平行四边形,
∴AB=CD
又AB=AC,
∴AC=CD
∴□ACDE是菱形.
典型例题
例2.如图,在四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为点
E,F.
(1)请你只添加一个条件(不另加辅助线),使得四边形AECF 为平行四边形.你添加的条件是________;
(2)添加了条件后,证明四边形AECF为平行四边形.
(1)由题意可知AE∥CF,要使得四边形AECF为平行四边形,则使得AF∥CE即可,从而添加适当条件即可;
(2)根据(1)的思路,利用平行四边形的定义证明即可.
(1)显然,直接添加AF∥CE,可根据定义得到结果,
(2)证明:∵ AE⊥BD,CF⊥BD,
∴AE∥CF
∵AF∥CE
∴四边形AECF为平行四边形.
AF∥CE
典型例题
若选②,即OE=OF;根据平行四边形的性质可得BO=DO,然后即可证明四边形BEDF是平行四边形,进而可得结论;若选①,即AE=CF;根据平行四边形的性质得出OE=OF后,同上面的思路解答即可;若选③,即BE∥DF,则∠BEO=∠DFO,再根据平行四边形的性质可证△BOE≌△DOF,于是可得结论.
解:若选②,即OE=OF;
证明:∵四边形ABCD是平行四边形,
∴BO=DO,
∵OE=OF,
∴四边形BEDF是平行四边形,∴BE=DF;
若选①,即AE=CF;
证明:∵四边形ABCD是平行四边形,
∴BO=DO,AO=CO,
∵AE=CF,∴OE=OF,
∴四边形BEDF是平行四边形
∴BE=DF;
若选③,即BE∥DF;
证明:∵四边形ABCD是平行四边形,
∴BO=DO,
∵BE∥DF;
∴∠BEO=∠DFO,
又∠BOE=∠DOF,
∴△BOE≌△DOF(AAS),
∴BE=DF;
拓展提高
(1)①利用平行四边形的性质和角平分线的定义先分别求出DE=AD=5,BC=CF=5,即可完成求解.
②证明出EF=CD即可完成求解.
拓展提高
(1)①利用平行四边形的性质和角平分线的定义先分别求出DE=AD=5,BC=CF=5,即可完成求解.
(1)①如图1,四边形ABCD是平行四边形,
∴AB∥CD, ∴∠DEA=∠EAB,
∵AE平分∠DAB ∴∠DAE=∠EAB
∴∠DAE=∠DEA ∴DE=AD=5
同理可得:BC=CF=5
∵点E与点F重合 ∴AB=CD=10
拓展提高
②证明出EF=CD即可完成求解.
②如图2,点E与点C重合,
同理可证DE=DC=AD=5
∴□ABCD是菱形
∵CF=BC=5
∴点F与点D重合
∴EF=DC=5
拓展提高
(2)本小题由于E、F点的位置不确定,故应先分情况讨论,再根据每种情况,利用DE=AD,CF=CB以及点 C,D,E,F相邻两点间的距离相等建立相等关系求解即可.
拓展提高
(2)本小题由于E、F点的位置不确定,故应先分情况讨论,再根据每种情况,利用DE=AD,CF=CB以及点 C,D,E,F相邻两点间的距离相等建立相等关系求解即可.
如图,在□ABCD中,∠DAB,∠ABC的平分线AE,BF分别与直线CD交于点E,F,当点C,D,E,F相邻两点间的距离相等时,求 的值.
(2)情况1,如图3,
可得AD=DE=EF=FC,
∴
情况2,如图4,
同理可得,AD=DE,BC=CF
又∵DF=FE=CE
∴
情况3,如图5,
由上,同理可得,AD=DE,BC=CF
又∵FD=DC=CE
∴
综上: 的值 或 或2.
谢 谢
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
