苏科版九年级下册7.1勾股定理及其逆定理 课件(共18张PTT)
文档属性
| 名称 | 苏科版九年级下册7.1勾股定理及其逆定理 课件(共18张PTT) |  | |
| 格式 | pptx | ||
| 文件大小 | 307.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-05 12:08:28 | ||
图片预览




文档简介
(共18张PPT)
7.1 勾股定理及其逆定理
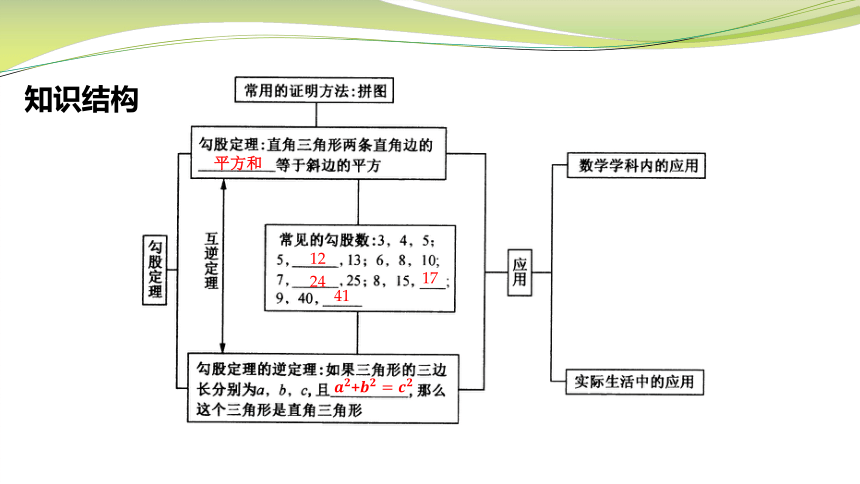
知识结构
平方和
+
12
24
17
41
勾股定理的证明
——拼图法
赵爽弦图
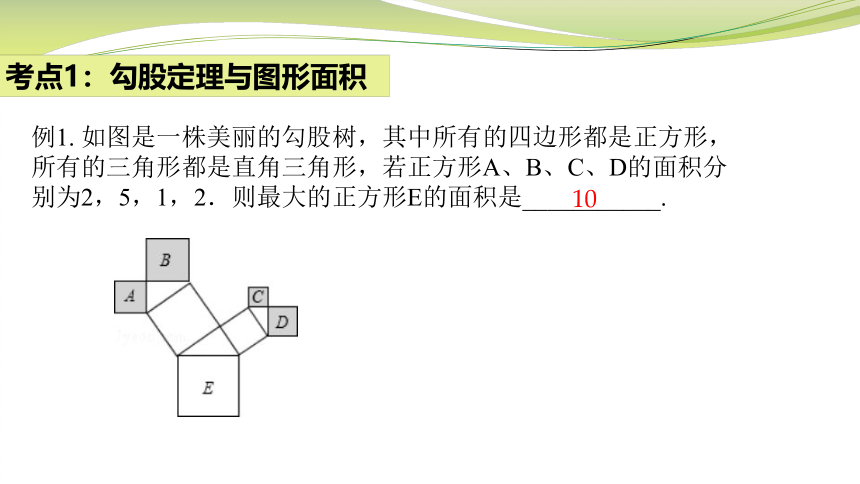
考点1:勾股定理与图形面积
例1. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别为2,5,1,2.则最大的正方形E的面积是___________.
10
变式训练1
2. 如图,已知1号、4号两个正方形的面积为7,2号、3号两个正方形的面积和为4,则a,b,c三个方形的面积和为______.
1. 如图,阴影部分是以直角三角形的三边为直径的半圆,两个小半圆的面积和为100,则大的半圆面积是__________.
15
100
3.一直角三角形的两边长分别为3和4.则第三边的长为________.
1.在Rt△ABC中,∠C=90°,AC:BC=3:4,AB=25,则AC=_____.BC=______.
2.若直角三角形中,一斜边比一直角边大2,且另一直角边长为6,则斜边的长______.
4.等腰三角形ABC的面积为12,底上的高AD为4,则它的腰长为__________.
5.等腰三角形的周长是36 cm,底边上的高是6 cm,则它的面积为_______.
15
20
10
5
48
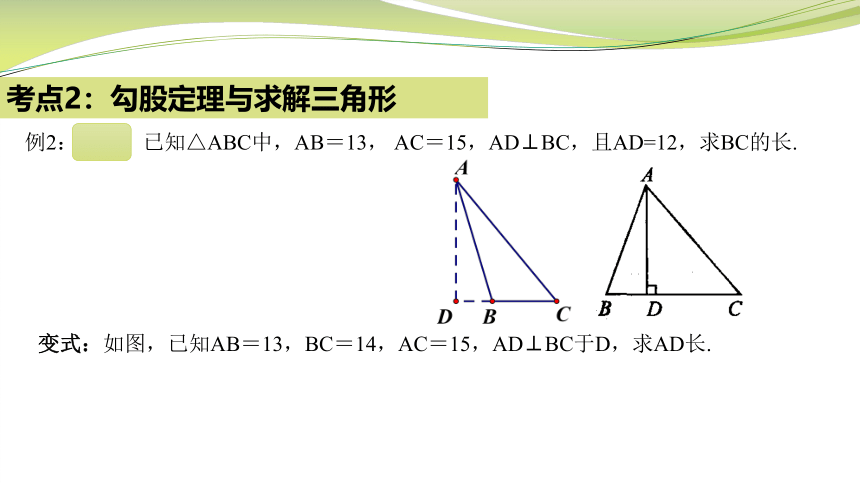
考点2:勾股定理与求解三角形
考点2:勾股定理与求解三角形
例2:如图,已知△ABC中,AB=13, AC=15,AD⊥BC,且AD=12,求BC的长.
变式:如图,已知AB=13,BC=14,AC=15,AD⊥BC于D,求AD长.
考点3:勾股定理与图形折叠
例3.如图,有一块直角三角形纸片,两直角边AC=6cm, BC=8cm,现将直角边AC沿直线折叠,使它落在斜边AB上,且点C落到E点,求△ACD的面积是多少
变式训练3
1.如图,折叠长方形纸片ABCD,使得点D落在边BC上的点F处,折痕为AE,AB=CD=6,AD=BC=10,试求EC的长度.
变式训练3
2. 如图1,有一张矩形纸片ABCD,其中AD=8cm,AB=6cm,将矩形纸片先沿对角线BD对折,点C落在点C'的位置,BC'交AD于点G.
(1)求证:AG=C'G;
(2)如图2,再折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M,求EM的长.
考点4:利用勾股定理逆定理求面积
例4.如图,在正方形ABCD 中AB=4, 点E是CD的中点,点F 在BC上,且FC=1 .则△AEF 的面积是____________
5
1.如图,学校操场边有一块四边形空地ABCD,其中AB⊥AC,AB=CD=4m,BC=9m,AD=7m.为了美化校园环境,创建绿色校园,学校计划将这块四边形空地进行绿化整理.
(1)求需要绿化的空地ABCD的面积;
(2)为方便师生出入,设计了过点A的小路AE,且AE⊥BC于点E,试求小路AE的长.
变式训练4
例5.如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C=___________度.
135
考点4:利用勾股定理逆定理求角度
1.如图,等边△ABC内有一点P,若点P到顶点A、B、C的距离分别为3、4、5,求∠APB的度数.
变式训练5
考点6:赵爽弦图
例1. 下图2是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,在Rt△ABC中,若直角边AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图3所示的“数学风车”,则这个风车的外围周长(图3中的实线)是_______.
76
变式训练6
1. 如图,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案.已知大正方形面积为49,小正方形面积为4.若用x,y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49;②x-y=2;③2xy+4=49;④x+y=9,其中说法正确的是( )
B
A.①② B.①②③ C.①②④ D.①②③④
2.我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图5).图6由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3,若S1+S2+S3=10,则S2的值是___________.
谢谢大家!
7.1 勾股定理及其逆定理
知识结构
平方和
+
12
24
17
41
勾股定理的证明
——拼图法
赵爽弦图
考点1:勾股定理与图形面积
例1. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别为2,5,1,2.则最大的正方形E的面积是___________.
10
变式训练1
2. 如图,已知1号、4号两个正方形的面积为7,2号、3号两个正方形的面积和为4,则a,b,c三个方形的面积和为______.
1. 如图,阴影部分是以直角三角形的三边为直径的半圆,两个小半圆的面积和为100,则大的半圆面积是__________.
15
100
3.一直角三角形的两边长分别为3和4.则第三边的长为________.
1.在Rt△ABC中,∠C=90°,AC:BC=3:4,AB=25,则AC=_____.BC=______.
2.若直角三角形中,一斜边比一直角边大2,且另一直角边长为6,则斜边的长______.
4.等腰三角形ABC的面积为12,底上的高AD为4,则它的腰长为__________.
5.等腰三角形的周长是36 cm,底边上的高是6 cm,则它的面积为_______.
15
20
10
5
48
考点2:勾股定理与求解三角形
考点2:勾股定理与求解三角形
例2:如图,已知△ABC中,AB=13, AC=15,AD⊥BC,且AD=12,求BC的长.
变式:如图,已知AB=13,BC=14,AC=15,AD⊥BC于D,求AD长.
考点3:勾股定理与图形折叠
例3.如图,有一块直角三角形纸片,两直角边AC=6cm, BC=8cm,现将直角边AC沿直线折叠,使它落在斜边AB上,且点C落到E点,求△ACD的面积是多少
变式训练3
1.如图,折叠长方形纸片ABCD,使得点D落在边BC上的点F处,折痕为AE,AB=CD=6,AD=BC=10,试求EC的长度.
变式训练3
2. 如图1,有一张矩形纸片ABCD,其中AD=8cm,AB=6cm,将矩形纸片先沿对角线BD对折,点C落在点C'的位置,BC'交AD于点G.
(1)求证:AG=C'G;
(2)如图2,再折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M,求EM的长.
考点4:利用勾股定理逆定理求面积
例4.如图,在正方形ABCD 中AB=4, 点E是CD的中点,点F 在BC上,且FC=1 .则△AEF 的面积是____________
5
1.如图,学校操场边有一块四边形空地ABCD,其中AB⊥AC,AB=CD=4m,BC=9m,AD=7m.为了美化校园环境,创建绿色校园,学校计划将这块四边形空地进行绿化整理.
(1)求需要绿化的空地ABCD的面积;
(2)为方便师生出入,设计了过点A的小路AE,且AE⊥BC于点E,试求小路AE的长.
变式训练4
例5.如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C=___________度.
135
考点4:利用勾股定理逆定理求角度
1.如图,等边△ABC内有一点P,若点P到顶点A、B、C的距离分别为3、4、5,求∠APB的度数.
变式训练5
考点6:赵爽弦图
例1. 下图2是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,在Rt△ABC中,若直角边AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图3所示的“数学风车”,则这个风车的外围周长(图3中的实线)是_______.
76
变式训练6
1. 如图,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案.已知大正方形面积为49,小正方形面积为4.若用x,y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49;②x-y=2;③2xy+4=49;④x+y=9,其中说法正确的是( )
B
A.①② B.①②③ C.①②④ D.①②③④
2.我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图5).图6由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3,若S1+S2+S3=10,则S2的值是___________.
谢谢大家!
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
