苏科版九年级下册7.2锐角三角函数 课件(共24张PPT)
文档属性
| 名称 | 苏科版九年级下册7.2锐角三角函数 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 613.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-05 12:10:33 | ||
图片预览



文档简介
(共24张PPT)
7.2锐角三角函数(复习)苏科版义务教育教科书《数学》九年级下册
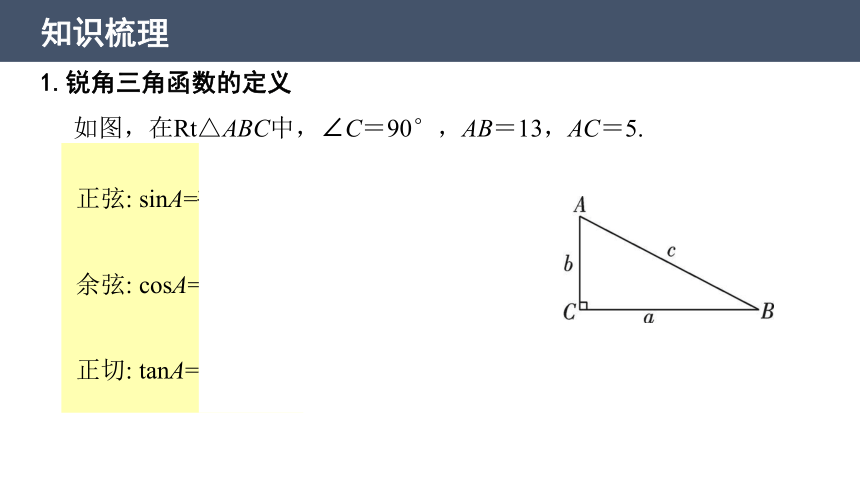
如图,在Rt△ABC中,∠C=90°,AB=13,AC=5.
知识梳理
正弦: sinA== ;
余弦: cosA== ;
正切: tanA== .
1.锐角三角函数的定义
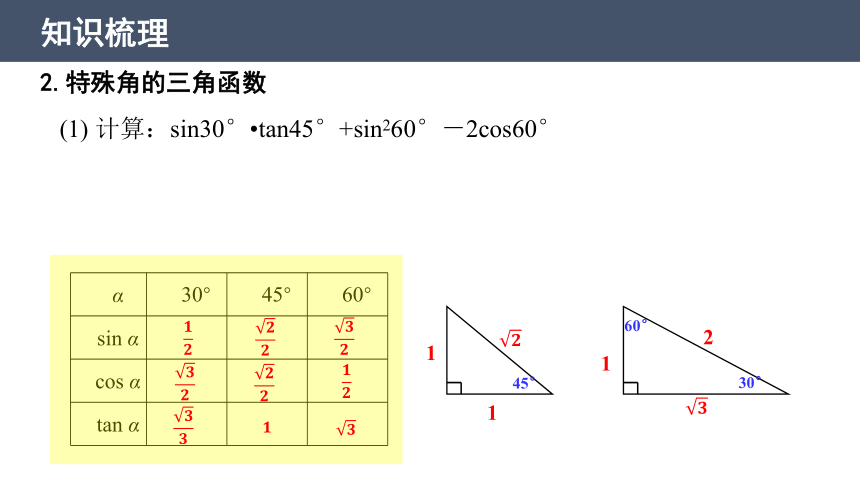
2.特殊角的三角函数
(1) 计算:sin30° tan45°+sin260°-2cos60°
α 30° 45° 60°
sin α
cos α
tan α
30°
60°
45°
1
1
1
2
知识梳理
2.特殊角的三角函数
(2)在△ABC中,∠A、∠B都是锐角,已知sinA=,cosB=,则∠C= .
(3)已知α是锐角,tan(α-15°)= 则sinα的值为 .
知识梳理
如图,在△ABC中,∠C=90°,AB=6,AC=3,求出其余边和角.
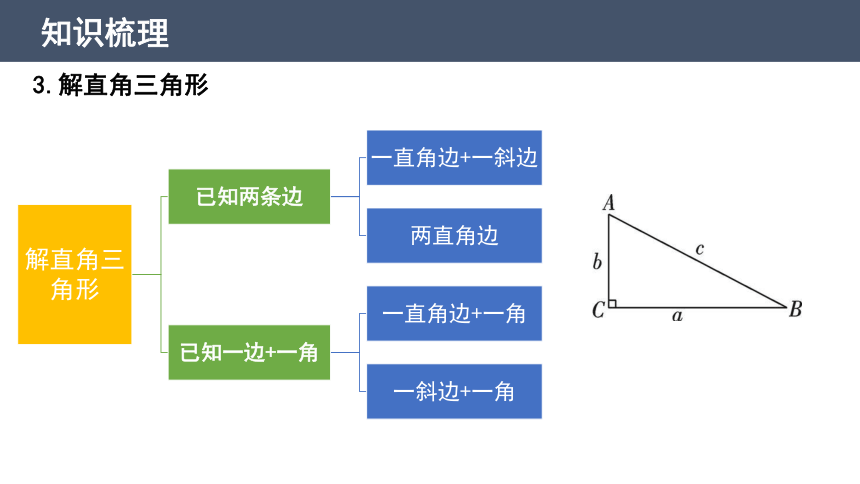
3.解直角三角形
解直角三角形:在直角三角形中,除直角外,共有5个元素,即3条边和2个锐角,由已知元素,求出所有未知元素的过程.
知识梳理
3.解直角三角形
知识梳理
解直角三角形至少知道几个元素?
3.解直角三角形
知识梳理
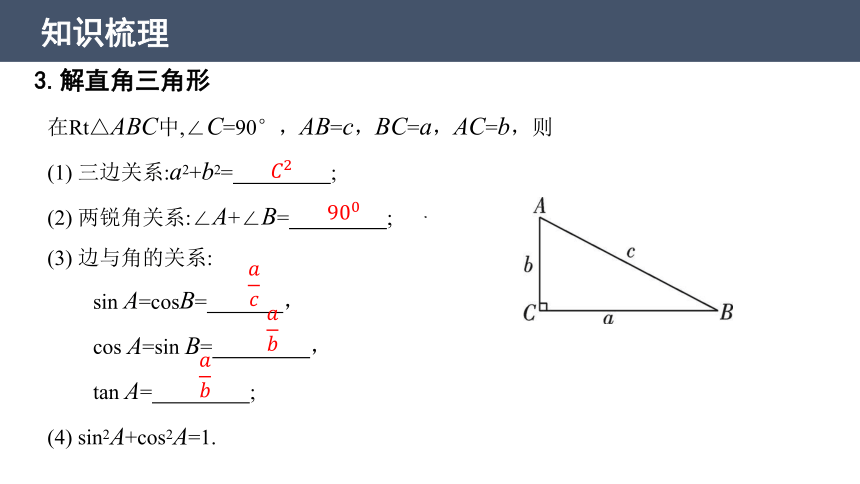
3.解直角三角形
在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b,则
(1) 三边关系:a2+b2= ;
(2) 两锐角关系:∠A+∠B= ;
(3) 边与角的关系:
sin A=cosB= ,
cos A=sin B= ,
tan A= ;
(4) sin2A+cos2A=1.
知识梳理
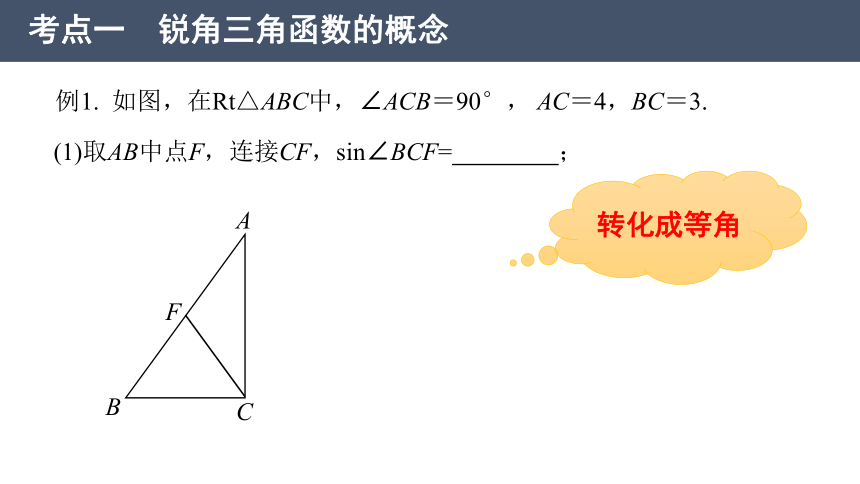
考点一 锐角三角函数的概念
例1. 如图,在Rt△ABC中,∠ACB=90°, AC=4,BC=3.
A
B
C
(1)取AB中点F,连接CF,sin∠BCF= ;
F
转化成等角
例1. 如图,在Rt△ABC中,∠ACB=90°, AC=4,BC=3.
(2)将△ABC沿AC翻折,得到△ADC,取AD中点G,则tan∠GBC= ;
G
A
B
C
D
构造直角三角形
考点一 锐角三角函数的概念
(3)将△ABC沿AC翻折,得到△ADC,再将△ADC沿AD翻折,得到△ADE,连接BE,则tan∠EBC的值为 .
例1. 如图,在Rt△ABC中,∠ACB=90°, AC=4,BC=3.
A
B
C
D
E
考点一 锐角三角函数的概念
H
构造基本
图形1
F
A
B
C
D
E
考点一 锐角三角函数的概念
H
M
构造基本
图形2
一题多解
例2 如图,△ABC的顶点是正方形网格的格点,则cos∠ABC的值为 .
考点二 网格中的锐角三角函数
A
B
C
策略一:顶点在格点,借助网格,连线构造格点直角三角形.
A
D
C
P
E
变式1. 如图正方形网格,则tan∠APD的值为 .
A
D
C
P
E
策略二:顶点不在格点,平移至格点,连线构造格点直角三角形.
考点二 网格中的锐角三角函数
A
F
C
变式2. 如图正方形网格,则sin∠FAC的值为 .
策略三:做垂线,构造直角三角形(等面积法).
考点二 网格中的锐角三角函数
例3. 如图,在△ABC中,∠A=30°,∠B=45°,AC=.
求BC与AB的长.
解:过点C作CD⊥AB于点D.
∵ ∠A=30°,AC=,
cos A=cos 30°==,
∴ AD=.
∵ sin A=sin 30°==,∴ CD=.
∵ tan B=tan 45°==1,∴ BD=.
∴ 在Rt△BCD中,BC==.∴ AB=AD+BD=
D
C
A
B
特殊角,构造直角三角形
考点三 解直角三角形的简单应用
变式1: 如图,在△ABC中,∠A=30°,∠B=45°,AB=1.
求AC与BC的长.
考点三 解直角三角形的简单应用
D
C
A
B
方程思想
变式2:如图,在△ABC中,∠A=30°,∠B=135°,AC=.
求BC与AB的长.
C
A
B
D
考点三 解直角三角形的简单应用
找特殊角,构造直角三角形
考点三 解直角三角形的简单应用
C
A
B
D
D
C
A
B
作垂直,构造含特殊角的直角三角形!
考点四 圆中的锐角三角函数
例4. 如图,AB是⊙O的直径,AB=10,AC=6,则cos ∠ADC的值为________.
利用直径所对的圆周角是直角构造直角三角形
例5. 如图,AD是⊙O的直径,BD、BC都是弦,且BD=BC,经过点B作⊙O的切线交AD的延长线于点E.
求证:∠EBD=∠CAB;
连接OB.∵ BE是⊙O的切线,∴ OB⊥BE.
∴ ∠OBD+∠EBD=90°.
∵ AD是⊙O的直径,∴ ∠ABD=90°.
∴ ∠ABO+∠OBD=90°.
∴ ∠EBD=∠ABO.
∵ OA=OB,∴ ∠OAB=∠ABO.
∴ ∠OAB=∠EBD.∵ BD=BC,∴ =.∴ ∠BAD=∠CAB.
∴ ∠EBD=∠CAB
考点四 圆中的锐角三角函数
(2)若BC=,AC=5,求sin ∠E的值.
利用切线与相关半径的关系构造直角三角形
考点四 圆中的锐角三角函数
M
一题多解
课堂小结
谢 谢!苏科版义务教育教科书《数学》九年级下册
7.2锐角三角函数(复习)苏科版义务教育教科书《数学》九年级下册
如图,在Rt△ABC中,∠C=90°,AB=13,AC=5.
知识梳理
正弦: sinA== ;
余弦: cosA== ;
正切: tanA== .
1.锐角三角函数的定义
2.特殊角的三角函数
(1) 计算:sin30° tan45°+sin260°-2cos60°
α 30° 45° 60°
sin α
cos α
tan α
30°
60°
45°
1
1
1
2
知识梳理
2.特殊角的三角函数
(2)在△ABC中,∠A、∠B都是锐角,已知sinA=,cosB=,则∠C= .
(3)已知α是锐角,tan(α-15°)= 则sinα的值为 .
知识梳理
如图,在△ABC中,∠C=90°,AB=6,AC=3,求出其余边和角.
3.解直角三角形
解直角三角形:在直角三角形中,除直角外,共有5个元素,即3条边和2个锐角,由已知元素,求出所有未知元素的过程.
知识梳理
3.解直角三角形
知识梳理
解直角三角形至少知道几个元素?
3.解直角三角形
知识梳理
3.解直角三角形
在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b,则
(1) 三边关系:a2+b2= ;
(2) 两锐角关系:∠A+∠B= ;
(3) 边与角的关系:
sin A=cosB= ,
cos A=sin B= ,
tan A= ;
(4) sin2A+cos2A=1.
知识梳理
考点一 锐角三角函数的概念
例1. 如图,在Rt△ABC中,∠ACB=90°, AC=4,BC=3.
A
B
C
(1)取AB中点F,连接CF,sin∠BCF= ;
F
转化成等角
例1. 如图,在Rt△ABC中,∠ACB=90°, AC=4,BC=3.
(2)将△ABC沿AC翻折,得到△ADC,取AD中点G,则tan∠GBC= ;
G
A
B
C
D
构造直角三角形
考点一 锐角三角函数的概念
(3)将△ABC沿AC翻折,得到△ADC,再将△ADC沿AD翻折,得到△ADE,连接BE,则tan∠EBC的值为 .
例1. 如图,在Rt△ABC中,∠ACB=90°, AC=4,BC=3.
A
B
C
D
E
考点一 锐角三角函数的概念
H
构造基本
图形1
F
A
B
C
D
E
考点一 锐角三角函数的概念
H
M
构造基本
图形2
一题多解
例2 如图,△ABC的顶点是正方形网格的格点,则cos∠ABC的值为 .
考点二 网格中的锐角三角函数
A
B
C
策略一:顶点在格点,借助网格,连线构造格点直角三角形.
A
D
C
P
E
变式1. 如图正方形网格,则tan∠APD的值为 .
A
D
C
P
E
策略二:顶点不在格点,平移至格点,连线构造格点直角三角形.
考点二 网格中的锐角三角函数
A
F
C
变式2. 如图正方形网格,则sin∠FAC的值为 .
策略三:做垂线,构造直角三角形(等面积法).
考点二 网格中的锐角三角函数
例3. 如图,在△ABC中,∠A=30°,∠B=45°,AC=.
求BC与AB的长.
解:过点C作CD⊥AB于点D.
∵ ∠A=30°,AC=,
cos A=cos 30°==,
∴ AD=.
∵ sin A=sin 30°==,∴ CD=.
∵ tan B=tan 45°==1,∴ BD=.
∴ 在Rt△BCD中,BC==.∴ AB=AD+BD=
D
C
A
B
特殊角,构造直角三角形
考点三 解直角三角形的简单应用
变式1: 如图,在△ABC中,∠A=30°,∠B=45°,AB=1.
求AC与BC的长.
考点三 解直角三角形的简单应用
D
C
A
B
方程思想
变式2:如图,在△ABC中,∠A=30°,∠B=135°,AC=.
求BC与AB的长.
C
A
B
D
考点三 解直角三角形的简单应用
找特殊角,构造直角三角形
考点三 解直角三角形的简单应用
C
A
B
D
D
C
A
B
作垂直,构造含特殊角的直角三角形!
考点四 圆中的锐角三角函数
例4. 如图,AB是⊙O的直径,AB=10,AC=6,则cos ∠ADC的值为________.
利用直径所对的圆周角是直角构造直角三角形
例5. 如图,AD是⊙O的直径,BD、BC都是弦,且BD=BC,经过点B作⊙O的切线交AD的延长线于点E.
求证:∠EBD=∠CAB;
连接OB.∵ BE是⊙O的切线,∴ OB⊥BE.
∴ ∠OBD+∠EBD=90°.
∵ AD是⊙O的直径,∴ ∠ABD=90°.
∴ ∠ABO+∠OBD=90°.
∴ ∠EBD=∠ABO.
∵ OA=OB,∴ ∠OAB=∠ABO.
∴ ∠OAB=∠EBD.∵ BD=BC,∴ =.∴ ∠BAD=∠CAB.
∴ ∠EBD=∠CAB
考点四 圆中的锐角三角函数
(2)若BC=,AC=5,求sin ∠E的值.
利用切线与相关半径的关系构造直角三角形
考点四 圆中的锐角三角函数
M
一题多解
课堂小结
谢 谢!苏科版义务教育教科书《数学》九年级下册
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
