苏科版 九年级下册7.5解直角三角形的应用 课件(共24张PPT)
文档属性
| 名称 | 苏科版 九年级下册7.5解直角三角形的应用 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-05 15:48:30 | ||
图片预览


文档简介
(共24张PPT)
7.3解直角三角形的应用(复习)苏科版义务教育教科书《数学》九年级下册
知识梳理
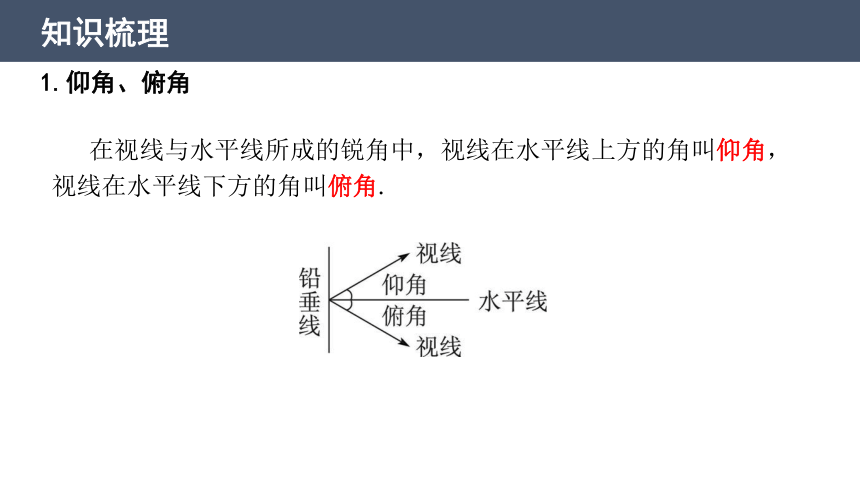
1.仰角、俯角
在视线与水平线所成的锐角中,视线在水平线上方的角叫仰角,
视线在水平线下方的角叫俯角.
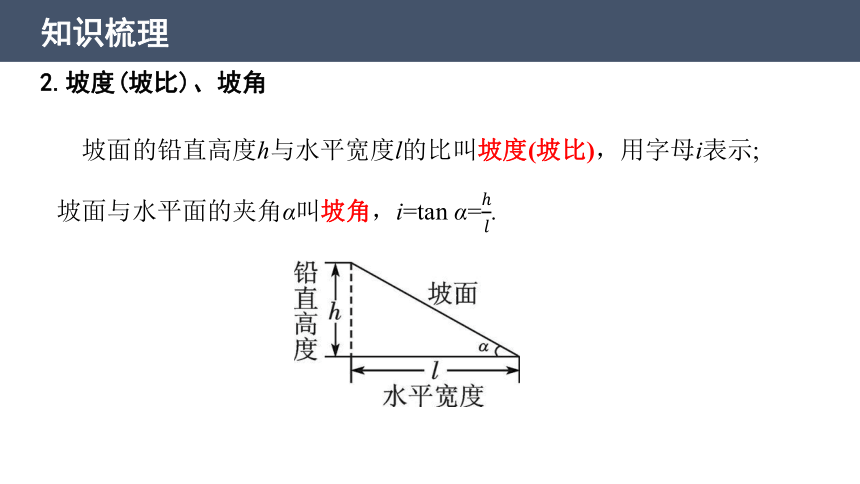
2.坡度(坡比)、坡角
知识梳理
坡面的铅直高度h与水平宽度l的比叫坡度(坡比),用字母i表示;
坡面与水平面的夹角α叫坡角,i=tan α=.
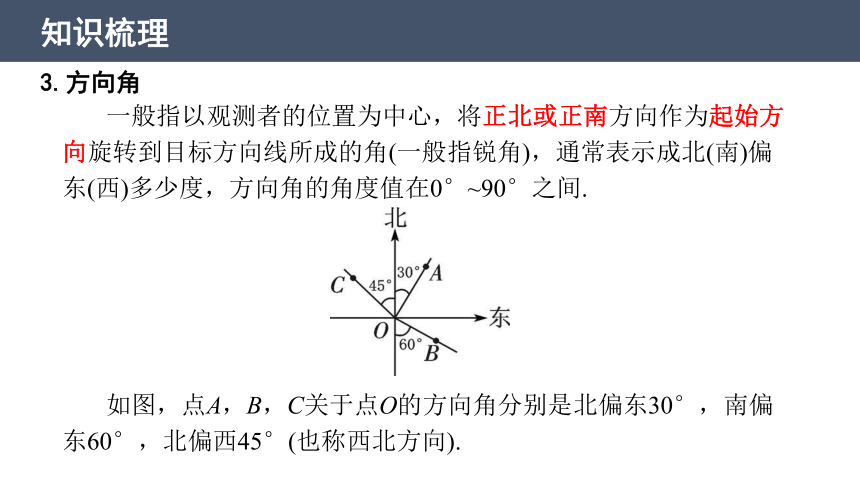
3.方向角
知识梳理
一般指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标方向线所成的角(一般指锐角),通常表示成北(南)偏东(西)多少度,方向角的角度值在0°~90°之间.
如图,点A,B,C关于点O的方向角分别是北偏东30°,南偏东60°,北偏西45°(也称西北方向).
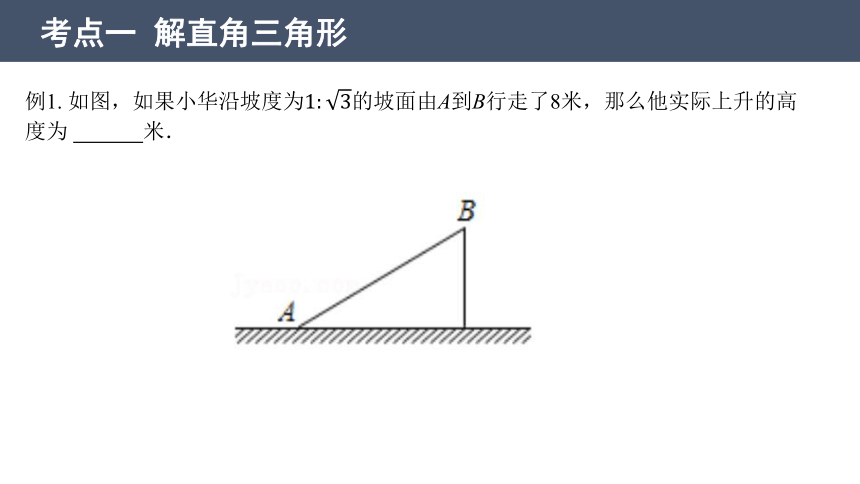
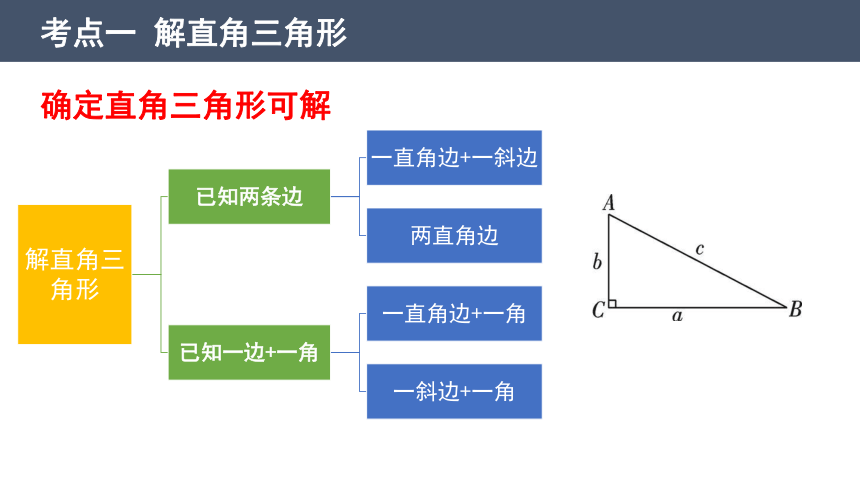
考点一 解直角三角形
例1. 如图,如果小华沿坡度为的坡面由A到B行走了8米,那么他实际上升的高度为 米.
考点一 解直角三角形
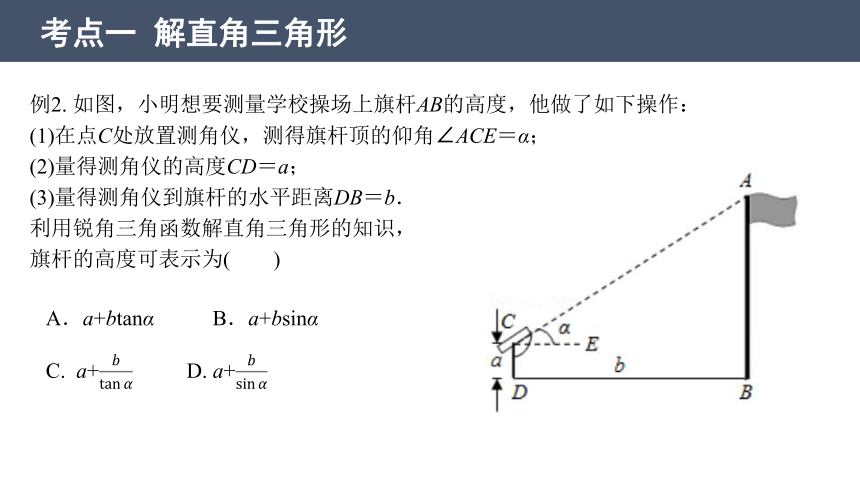
例2. 如图,小明想要测量学校操场上旗杆AB的高度,他做了如下操作:
(1)在点C处放置测角仪,测得旗杆顶的仰角∠ACE=α;
(2)量得测角仪的高度CD=a;
(3)量得测角仪到旗杆的水平距离DB=b.
利用锐角三角函数解直角三角形的知识,
旗杆的高度可表示为( )
A.a+btanα B.a+bsinα
C. a+ D. a+
考点一 解直角三角形
例3. 如图,明年舟山将再添一个最高颜值城市新地标,新城长峙岛上将矗立起一座摩天轮,其直径为90m,旋转1周用时15min.小明从摩天轮的底部(与地面相距0.5m)出发开始观光,摩天轮转动1周,小明在离地面23m以上的空中有多长时间?( )
A.3min B.5min C.6min D.10min
考点一 解直角三角形
确定直角三角形可解
考点二 基本模型
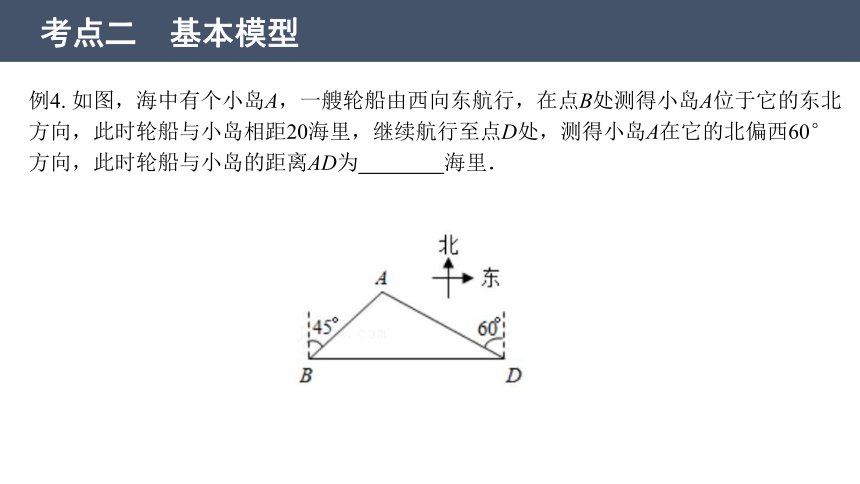
例4. 如图,海中有个小岛A,一艘轮船由西向东航行,在点B处测得小岛A位于它的东北方向,此时轮船与小岛相距20海里,继续航行至点D处,测得小岛A在它的北偏西60°方向,此时轮船与小岛的距离AD为 海里.
考点二 基本模型
例5. 如图,从楼顶A处看楼下荷塘C处的俯角为45°,看楼下荷塘D处的俯角为60°,已知楼高AB为30米,则荷塘的宽CD为 米(结果保留根号).
考点二 基本模型
共边双直角三角形
考点二 基本模型
共边双直角三角形
共边异侧
共边同侧
考点二 基本模型
例6. 如图,某大楼的顶部树有一块广告牌CD,李明在山坡的坡脚A处测得广告牌底部D的仰角为53°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:,AB=12米,AE=24米.(测角器的高度忽略不计,结果精确到0.1米,,,, )
(1)求点B距水平地面AE的高度;
(2)求广告牌CD的高度.
(1) 如图,过点B作BM⊥AE,
由题意可知,i=1:=tan∠BAM,
∴∠BAM=30°,
又∵ AB=12米,
∴BM=6米.
M
考点二 基本模型
M
N
(2)由(1)得:
NE=BM=6(米),AM=(米),
∴ME=AM+AE= (米),
∵∠CBN=45°,
∴CN=BN=ME = (米),
∴CE=CN+NE= 30 (米),
在Rt△ADE中,∠DAE=53°,AE=24米,
∴DE=AE tan53°≈24× =32(米),
∴CD=CE-DE = 30 -32≈8.4(米),
答:广告牌CD的高约8.4米.
考点二 基本模型
共边双直角三角形
共边异侧
共边同侧
(其他变式…)
(其他变式…)
平移
平移
考点二 基本模型
例7. 如图1为放置在水平桌面l上的台灯,底座的高AB为5cm,长度均为20cm的连杆BC,CD与AB始终在同一平面上.
(1)转动连杆BC,CD,使∠BCD成平角,∠ABC=150°,如图2,求连杆端点D离桌面l的高度DE.
(2)将(1)中的连杆CD再绕点C逆时针旋转,使∠BCD=165°,如图3,问此时连杆端点D离桌面l的高度是增加还是减少?增加或减少了多少?(精确到0.1cm,参考数据:
考点二 基本模型
(1)转动连杆BC,CD,使∠BCD成平角,∠ABC=150°,如图2,求连杆端点D离桌面l的高度DE.
(1)如图2中,作BO⊥DE于O.
∵∠OEA=∠BOE=∠BAE=90°,
∴四边形ABOE是矩形,
∴∠OBA=90°,
∴∠DBO=150°-90°=60°,
∴OD=BD sin60°=
∴DE=OD+OE=OD+AB
=+5≈39.6(cm).
O
考点二 基本模型
(2)将(1)中的连杆CD再绕点C逆时针旋转,使∠BCD=165°,如图3,问此时连杆端点D离桌面l的高度是增加还是减少?增加或减少了多少?(精确到0.1cm,参考数据:
(2)作DF⊥l于F,CP⊥DF于P,
BG⊥DF于G,CH⊥BG于H.
则四边形PCHG是矩形,
∵∠CBH=60°,∠CHB=90°,
∴∠BCH=30°,∵∠BCD=165°,∴∠DCP=45°,
∴CH=BCsin60°=DP=CDsin45°=(cm),
∴DF=DP+PG+GF=DP+CH+AB= +5 (cm),
∴下降高度:
DE﹣DF= ≈3.2(cm).
O
F
H
G
P
考点二 基本模型
共边双直角三角形
共边异侧
共边同侧
(其他变式…)
(其他变式…)
平移
平移
解题策略:构造直角三角形,借助共边( 共线边 )传递条件,建立等量关系!
考点三 基于生活经验的建模
例8.图①是某小区折叠道闸的实景图,图②是其工作示意图,道闸由垂直于地面的立柱AB,CD和折叠杆“AE﹣EF”组成,其中AB=CD=1.2m,AB,CD之间的水平距离BD=2.5m,AE=1.5m.道闸工作时,折叠杆“AE﹣EF”可绕点A在一定范围内转动,张角为∠BAE(90°≤∠BAE≤150°),同时杆EF始终与地面BD保持平行.(参考数据:≈1.414,≈1.732)
(1)当张角∠BAE为135°时,求杆EF与地面BD之间的距离(结果精确到0.01m);
(2)试通过计算判断宽度为1.8m,高度为2.45m的小型厢式货车能否正常通过此道闸?
考点三 基于生活经验的建模
(1)当张角∠BAE为135°时,求杆EF与地面BD之间的距离(结果精确到0.01m);
(1)过点E作EM⊥BD,垂足为M,
交AC于点N,则EN⊥AC,
∵AB⊥BD,∴四边形ABMN是矩形,
∴AB=MN=1.2(米),∠BAN=90°,
∵∠BAE=135°,
∴∠EAN=∠BAE-∠BAN=45°,
在Rt△AEN中,EN=AEsin45°=1.5×(米),
∴EM=EN+MN= +1.2≈2.26(米),
答:杆EF与地面BD之间的距离为2.26米;
N
M
考点三 基于生活经验的建模
(2)试通过计算判断宽度为1.8m,高度为2.45m的小型厢式货车能否正常通过此道闸?
(2)如图,取DQ=1.8,
过点Q作GQ⊥BD
当QD=PC=1.8m,
∴BQ=AP=2.5﹣1.8=0.7m,
当∠BAE=150°时,
∴∠EAP=∠BAE﹣∠BAP=60°,
∴ GP=APtan60°= ≈1.212米,
∴GP+PQ=1.212+1.2=2.412米,
∵2.412<2.45,
∴宽度为1.8m,高度为2.45m的小型厢式货车不能正常通过此道闸.
G
P
Q
课堂小结
谢 谢!苏科版义务教育教科书《数学》九年级下册
7.3解直角三角形的应用(复习)苏科版义务教育教科书《数学》九年级下册
知识梳理
1.仰角、俯角
在视线与水平线所成的锐角中,视线在水平线上方的角叫仰角,
视线在水平线下方的角叫俯角.
2.坡度(坡比)、坡角
知识梳理
坡面的铅直高度h与水平宽度l的比叫坡度(坡比),用字母i表示;
坡面与水平面的夹角α叫坡角,i=tan α=.
3.方向角
知识梳理
一般指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标方向线所成的角(一般指锐角),通常表示成北(南)偏东(西)多少度,方向角的角度值在0°~90°之间.
如图,点A,B,C关于点O的方向角分别是北偏东30°,南偏东60°,北偏西45°(也称西北方向).
考点一 解直角三角形
例1. 如图,如果小华沿坡度为的坡面由A到B行走了8米,那么他实际上升的高度为 米.
考点一 解直角三角形
例2. 如图,小明想要测量学校操场上旗杆AB的高度,他做了如下操作:
(1)在点C处放置测角仪,测得旗杆顶的仰角∠ACE=α;
(2)量得测角仪的高度CD=a;
(3)量得测角仪到旗杆的水平距离DB=b.
利用锐角三角函数解直角三角形的知识,
旗杆的高度可表示为( )
A.a+btanα B.a+bsinα
C. a+ D. a+
考点一 解直角三角形
例3. 如图,明年舟山将再添一个最高颜值城市新地标,新城长峙岛上将矗立起一座摩天轮,其直径为90m,旋转1周用时15min.小明从摩天轮的底部(与地面相距0.5m)出发开始观光,摩天轮转动1周,小明在离地面23m以上的空中有多长时间?( )
A.3min B.5min C.6min D.10min
考点一 解直角三角形
确定直角三角形可解
考点二 基本模型
例4. 如图,海中有个小岛A,一艘轮船由西向东航行,在点B处测得小岛A位于它的东北方向,此时轮船与小岛相距20海里,继续航行至点D处,测得小岛A在它的北偏西60°方向,此时轮船与小岛的距离AD为 海里.
考点二 基本模型
例5. 如图,从楼顶A处看楼下荷塘C处的俯角为45°,看楼下荷塘D处的俯角为60°,已知楼高AB为30米,则荷塘的宽CD为 米(结果保留根号).
考点二 基本模型
共边双直角三角形
考点二 基本模型
共边双直角三角形
共边异侧
共边同侧
考点二 基本模型
例6. 如图,某大楼的顶部树有一块广告牌CD,李明在山坡的坡脚A处测得广告牌底部D的仰角为53°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:,AB=12米,AE=24米.(测角器的高度忽略不计,结果精确到0.1米,,,, )
(1)求点B距水平地面AE的高度;
(2)求广告牌CD的高度.
(1) 如图,过点B作BM⊥AE,
由题意可知,i=1:=tan∠BAM,
∴∠BAM=30°,
又∵ AB=12米,
∴BM=6米.
M
考点二 基本模型
M
N
(2)由(1)得:
NE=BM=6(米),AM=(米),
∴ME=AM+AE= (米),
∵∠CBN=45°,
∴CN=BN=ME = (米),
∴CE=CN+NE= 30 (米),
在Rt△ADE中,∠DAE=53°,AE=24米,
∴DE=AE tan53°≈24× =32(米),
∴CD=CE-DE = 30 -32≈8.4(米),
答:广告牌CD的高约8.4米.
考点二 基本模型
共边双直角三角形
共边异侧
共边同侧
(其他变式…)
(其他变式…)
平移
平移
考点二 基本模型
例7. 如图1为放置在水平桌面l上的台灯,底座的高AB为5cm,长度均为20cm的连杆BC,CD与AB始终在同一平面上.
(1)转动连杆BC,CD,使∠BCD成平角,∠ABC=150°,如图2,求连杆端点D离桌面l的高度DE.
(2)将(1)中的连杆CD再绕点C逆时针旋转,使∠BCD=165°,如图3,问此时连杆端点D离桌面l的高度是增加还是减少?增加或减少了多少?(精确到0.1cm,参考数据:
考点二 基本模型
(1)转动连杆BC,CD,使∠BCD成平角,∠ABC=150°,如图2,求连杆端点D离桌面l的高度DE.
(1)如图2中,作BO⊥DE于O.
∵∠OEA=∠BOE=∠BAE=90°,
∴四边形ABOE是矩形,
∴∠OBA=90°,
∴∠DBO=150°-90°=60°,
∴OD=BD sin60°=
∴DE=OD+OE=OD+AB
=+5≈39.6(cm).
O
考点二 基本模型
(2)将(1)中的连杆CD再绕点C逆时针旋转,使∠BCD=165°,如图3,问此时连杆端点D离桌面l的高度是增加还是减少?增加或减少了多少?(精确到0.1cm,参考数据:
(2)作DF⊥l于F,CP⊥DF于P,
BG⊥DF于G,CH⊥BG于H.
则四边形PCHG是矩形,
∵∠CBH=60°,∠CHB=90°,
∴∠BCH=30°,∵∠BCD=165°,∴∠DCP=45°,
∴CH=BCsin60°=DP=CDsin45°=(cm),
∴DF=DP+PG+GF=DP+CH+AB= +5 (cm),
∴下降高度:
DE﹣DF= ≈3.2(cm).
O
F
H
G
P
考点二 基本模型
共边双直角三角形
共边异侧
共边同侧
(其他变式…)
(其他变式…)
平移
平移
解题策略:构造直角三角形,借助共边( 共线边 )传递条件,建立等量关系!
考点三 基于生活经验的建模
例8.图①是某小区折叠道闸的实景图,图②是其工作示意图,道闸由垂直于地面的立柱AB,CD和折叠杆“AE﹣EF”组成,其中AB=CD=1.2m,AB,CD之间的水平距离BD=2.5m,AE=1.5m.道闸工作时,折叠杆“AE﹣EF”可绕点A在一定范围内转动,张角为∠BAE(90°≤∠BAE≤150°),同时杆EF始终与地面BD保持平行.(参考数据:≈1.414,≈1.732)
(1)当张角∠BAE为135°时,求杆EF与地面BD之间的距离(结果精确到0.01m);
(2)试通过计算判断宽度为1.8m,高度为2.45m的小型厢式货车能否正常通过此道闸?
考点三 基于生活经验的建模
(1)当张角∠BAE为135°时,求杆EF与地面BD之间的距离(结果精确到0.01m);
(1)过点E作EM⊥BD,垂足为M,
交AC于点N,则EN⊥AC,
∵AB⊥BD,∴四边形ABMN是矩形,
∴AB=MN=1.2(米),∠BAN=90°,
∵∠BAE=135°,
∴∠EAN=∠BAE-∠BAN=45°,
在Rt△AEN中,EN=AEsin45°=1.5×(米),
∴EM=EN+MN= +1.2≈2.26(米),
答:杆EF与地面BD之间的距离为2.26米;
N
M
考点三 基于生活经验的建模
(2)试通过计算判断宽度为1.8m,高度为2.45m的小型厢式货车能否正常通过此道闸?
(2)如图,取DQ=1.8,
过点Q作GQ⊥BD
当QD=PC=1.8m,
∴BQ=AP=2.5﹣1.8=0.7m,
当∠BAE=150°时,
∴∠EAP=∠BAE﹣∠BAP=60°,
∴ GP=APtan60°= ≈1.212米,
∴GP+PQ=1.212+1.2=2.412米,
∵2.412<2.45,
∴宽度为1.8m,高度为2.45m的小型厢式货车不能正常通过此道闸.
G
P
Q
课堂小结
谢 谢!苏科版义务教育教科书《数学》九年级下册
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
