广东省珠海市2012-2013学年高二上学期期末质检数学文试题(B卷)
文档属性
| 名称 | 广东省珠海市2012-2013学年高二上学期期末质检数学文试题(B卷) |  | |
| 格式 | zip | ||
| 文件大小 | 136.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-25 14:45:28 | ||
图片预览


文档简介
珠海市2012~2013学年度第一学期期末学生学业质量监测
高二文科数学试题(B卷)
时量:120分钟 分值:150分. 内容:圆,数学选修1-1和数学必修3.
一、选择题(本大题共12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的)
1.“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
2.抽查10件产品,设事件A:至少有两件次品,则与A的互斥的事件为( )
A.恰有两件次品 B.恰有一件次品 C.恰有两件正品 D.至少两件正品
3.已知函数,若,则( )
A. B. 或 C. D.
4.椭圆的离心率等于( )
A. B. C. D.2
5.抛物线的焦点坐标为 ( )
A . B. C. D.
6.下列求导运算正确的是( )
A. B.
C. D.
7.如某校高中三年级的300名学生已经编号为0,1,……,299,为了了解学生的学习情况,要抽取一个样本数为60的样本,用系统抽样的方法进行抽取,若第60段所抽到的编号为298,则第1段抽到的编号为( )
A.2 B.3 C.4 D.5
8.已知命题:,则( )
A. B.
C. D.
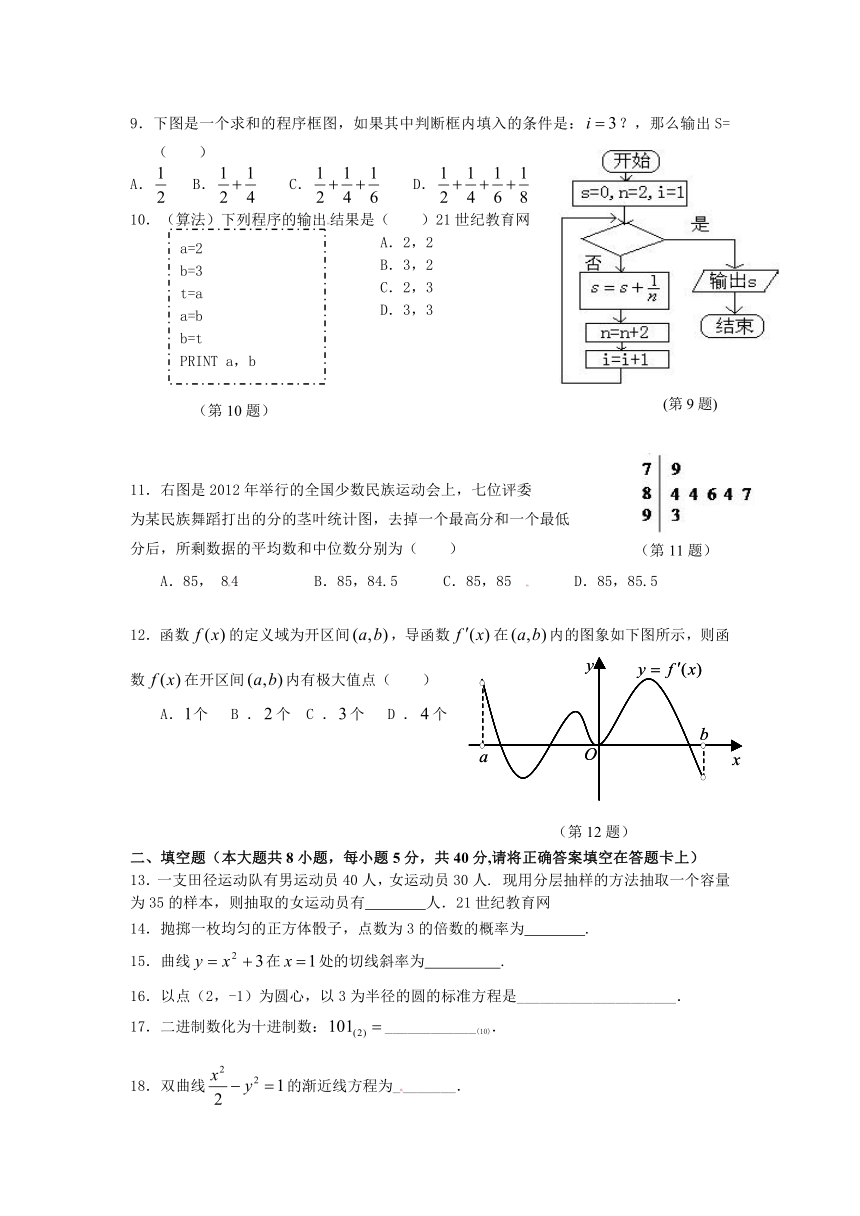
9.下图是一个求和的程序框图,如果其中判断框内填入的条件是:?,那么输出S=( )
A. B. C. D.
10.(算法)下列程序的输出结果是( )21世纪教育网
A.2,2
B.3,2
C.2,3
D.3,3
11.右图是2012年举行的全国少数民族运动会上,七位评委
为某民族舞蹈打出的分的茎叶统计图,去掉一个最高分和一个最低
分后,所剩数据的平均数和中位数分别为( )
A.85, 84 B.85,84.5 C.85,85 D.85,85.5
12.函数的定义域为开区间,导函数在内的图象如下图所示,则函数在开区间内有极大值点( )
A.个 B .个 C .个 D .个
二、填空题(本大题共8小题,每小题5分,共40分,请将正确答案填空在答题卡上)
13.一支田径运动队有男运动员40人,女运动员30人. 现用分层抽样的方法抽取一个容量为35的样本,则抽取的女运动员有 人.21世纪教育网
14.抛掷一枚均匀的正方体骰子,点数为3的倍数的概率为 .
15.曲线在处的切线斜率为 .
16.以点(2,-1)为圆心,以3为半径的圆的标准方程是_____________________.
17.二进制数化为十进制数:____________(10).
18.双曲线的渐近线方程为________.
19.为了了解“预防禽流感疫苗”的使用情况,某市卫生部门对本地区5月份至7月份使用疫苗的所有养鸡场进行了调查,根据下列图表提供的信息,可以得出这三个月本地区平均每月注射了疫苗的鸡的数量为 万只.
20.函数的极小值是 .21世纪教育网
三、解答题(本大题共5小题,每题10分,共50分.请将详细解答过程写在答题卡上)
21.设:P: 指数函数在x∈R内单调递减;Q:.如果P为真,Q为假,求a的取值范围.
22.已知M={3,6,7,8},N={3,4,5},从M和N中各自任取一个数,分别记为和为,求≥11的概率.
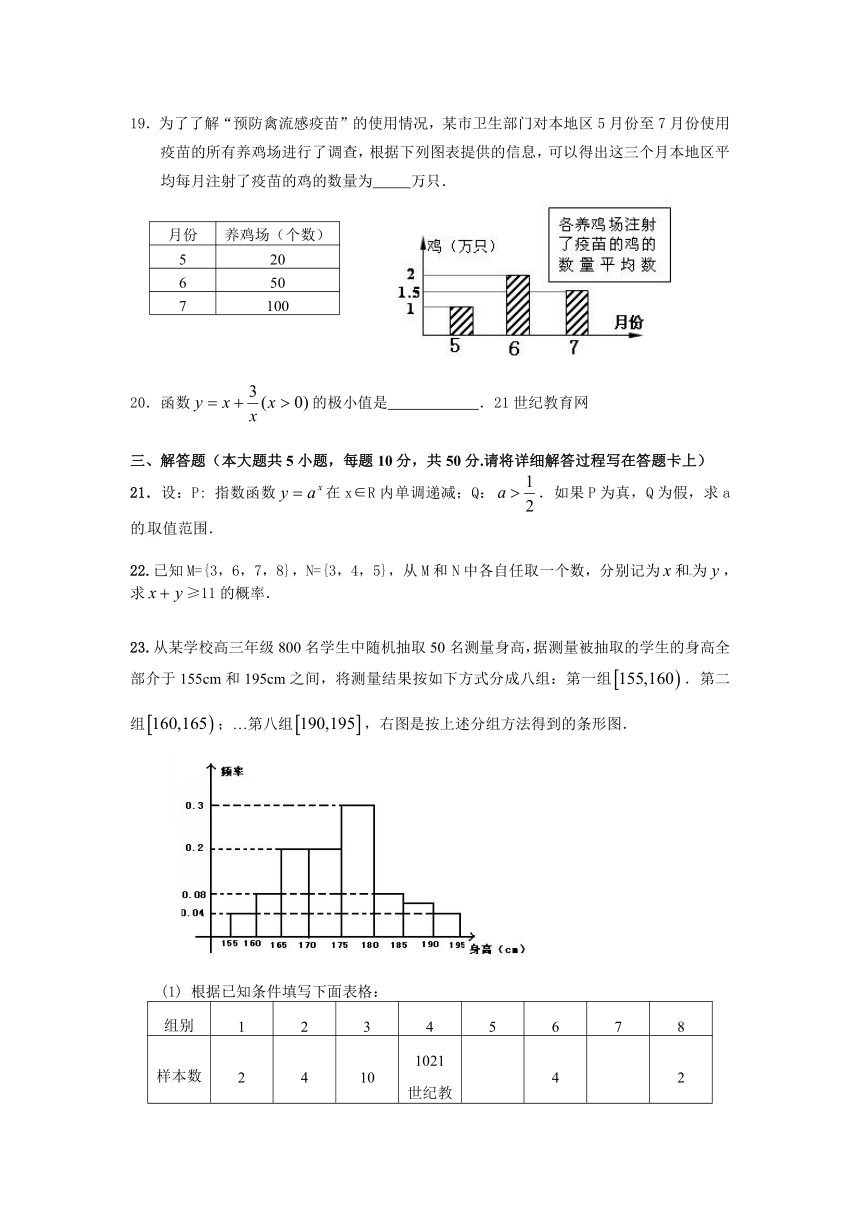
23.从某学校高三年级800名学生中随机抽取50名测量身高,据测量被抽取的学生的身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组.第二组;…第八组,右图是按上述分组方法得到的条形图.
(1) 根据已知条件填写下面表格:
组别
1
2
3
4
5
6
7
8
样本数
2
4
10
1021世纪教育网
4
2
(2) 估计这所学校高三年级800名学生中身高在180cm以上(含180cm)的人数.
24.已知点A(-2,0),B(2,0),直线AP与直线AB相交于点P,它们的斜率之积为,求点P的轨迹方程(化为标准方程).
25.已知函数.
(1)求;(2)求函数的单调区间.21世纪教育网21世纪教育网
珠海市2012~2013学年度第一学期期末学生学业质量监测
高二文科数学试题(B卷)与参考答案
时量:120分钟 分值:150分. 内容:数学选修1-1和数学必修3.
一、选择题(本大题共12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的)
1.(逻辑)“”是“”的( )
A.充分而不必要条件 B 必要而不充分条件
C.充分必要条件 D .既不充分也不必要条件
2.(概率)抽查10件产品,设事件A:至少有两件次品,则与A的互斥的事件为( )
A.恰有两件次品 B.恰有一件次品 C.恰有两件正品 D.至少两件正品
3.(导数)已知函数,若,则
A. B. 或 C. D.
4.(圆锥曲线)椭圆的离心率等于( )
A. B . C . D .2
5.(圆锥曲线)抛物线的焦点坐标为 ( )
A . B . C . D.
6.(导数)下列求导运算正确的是 ( )
A . B .
C . D.21世纪教育网
7.(统计)如某校高中三年级的300名学生已经编号为0,1,……,299,为了了解学生的学习情况,要抽取一个样本数为60的样本,用系统抽样的方法进行抽取,若第60段所抽到的编号为298,则第1段抽到的编号为( )
A.2 B.3 C.4 D.5
8.(逻辑)已知命题:,则( )
A. B.
C. D.
9.(算法)下图是一个求和的程序框图,如果其中判断框内填入的条件是:?,那么输出S=( )
A. B. C. D.
10.(算法)下列程序的输出结果是( )
A.2,2
B.3,2
C.2,3
D.3,3
11.(统计)右图是2012年举行的全国少数民族运动会上,七位评委
为某民族舞蹈打出的分的茎叶统计图,去掉一个最高分和一个最低
分后,所剩数据的平均数和中位数分别为( )。
A.85,84 B.85,84.5 C.,85 D.,85.5
12.(导数)函数的定义域为开区间,导函数在内的图象如下图所示,则函数在开区间内有极大值点( )
A.个 B .个 C .个 D .个
二、填空题(本大题共8小题,每小题5分,共40分,请将正确答案填空在答题卡上)
13.(统计)一支田径运动队有男运动员40人,女运动员30人. 现用分层抽样的方法抽取一个容量为35的样本,则抽取的女运动员有 人.15
14.(概率)抛掷一枚均匀的正方体骰子,点数为3的倍数的概率为 .1/3
15.(导数)曲线在处的切线斜率为 2
16.(圆)以点(2,-1)为圆心,以3为半径的圆的标准方程是_____________________.
17.(算法)二进制数化为十进制数:____________(10).5
18.(圆锥曲线)双曲线的渐近线方程为________.
19.(统计)为了了解“预防禽流感疫苗”的使用情况,某市卫生部门对本地区5月份至7月份使用疫苗的所有养鸡场进行了调查,根据下列图表提供的信息,可以得出这三个月本地区平均每月注射了疫苗的鸡的数量为 万只.90
20.(导数)函数的极小值是 .
三、解答题(本大题共5小题,每题10分,共50分.请将详细解答过程写在答题卡上)21世纪教育网
21.(逻辑估级2.5)设:P: 指数函数在x∈R内单调递减;Q:。如果P为真,Q为假,求a的取值范围。
解:当0 ∴P为真时,0∵Q为假, ∴…(5分)
由题意有P正确,且Q不正确,因此,a∈(0,1)∩…(8分)
即a∈…(10分)[来源:21世纪教育网]
22.(概率估级3)(本题满分10分) 21世纪教育网
已知M={3,6,7,8},N={3,4,5},从M和N中各自任取一个数,分别记为和为,求≥11的概率.
解:从M、N中各取一个数组成数对(x ,y),共有12对,…3分
其中满足的有:
(6,5),(7,4),(7,5),(8,3),(8,4),(8,5),共6对…6分[来源:21世纪教育网]
故所求概率为,所以使的概率为.…10分
23.(统计估级3)从某学校高三年级800名学生中随机抽取50名测量身高,据测量被抽取的学生的身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组.第二组;…第八组,右图是按上述分组方法得到的条形图.
(1) 根据已知条件填写下面表格:
组别
1
2
3
4
5
6
7
8
样本数
2
4
10
10
4
2
(2) 估计这所学校高三年级800名学生中身高在180cm以上(含180cm)的人数;
解: (Ⅰ)由条形图得第七组频率为
21世纪教育网
∴第七组的人数为3人……(2分)
0.3
∴第五组的人数为15人……(4分)
组别
1
2
3
4
5
6
7
8
样本中人数
2
4
10
10
15
4
3
2
(Ⅱ)由条形图得前五组频率为 (0.008+0.016+0.04+0.04+0.06)×5=0.82,
………………………………………6分
后三组频率为1-0.82=0.18 …………………………………8分
估计这所学校高三年级身高在180cm以上(含180cm)的人数:
800×0.18=144(人) …………………(10分)
24.(圆锥曲线估级4)已知点A(-2,0),B(2,0),直线AP与直线AB相交于点P,它们的斜率之积为,求点P的轨迹方程(化为标准方程).
解:设点P,21世纪教育网
直线AP的斜率…… (2分)
直线BP的斜率…… (4分)
根据已知,有:…… (7分)
化简得: ……… (10分)
(没有写扣1分)
25.(导数估级5)已知函数.
(1)求;(2)求函数的单调区间.
解:(1)∵,…… (2分)
∴…… (5分)
(2)∵
当时,也即当或时,单调递增;…… (7分)
当时,也即当时,单调递减;…… (9分)
∴函数的单调递增区间是和,单调递减区间是. (10分)
(在0,2处写成闭区间,也同样计分)
21世纪教育网
21世纪教育网
高二文科数学试题(B卷)
时量:120分钟 分值:150分. 内容:圆,数学选修1-1和数学必修3.
一、选择题(本大题共12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的)
1.“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
2.抽查10件产品,设事件A:至少有两件次品,则与A的互斥的事件为( )
A.恰有两件次品 B.恰有一件次品 C.恰有两件正品 D.至少两件正品
3.已知函数,若,则( )
A. B. 或 C. D.
4.椭圆的离心率等于( )
A. B. C. D.2
5.抛物线的焦点坐标为 ( )
A . B. C. D.
6.下列求导运算正确的是( )
A. B.
C. D.
7.如某校高中三年级的300名学生已经编号为0,1,……,299,为了了解学生的学习情况,要抽取一个样本数为60的样本,用系统抽样的方法进行抽取,若第60段所抽到的编号为298,则第1段抽到的编号为( )
A.2 B.3 C.4 D.5
8.已知命题:,则( )
A. B.
C. D.
9.下图是一个求和的程序框图,如果其中判断框内填入的条件是:?,那么输出S=( )
A. B. C. D.
10.(算法)下列程序的输出结果是( )21世纪教育网
A.2,2
B.3,2
C.2,3
D.3,3
11.右图是2012年举行的全国少数民族运动会上,七位评委
为某民族舞蹈打出的分的茎叶统计图,去掉一个最高分和一个最低
分后,所剩数据的平均数和中位数分别为( )
A.85, 84 B.85,84.5 C.85,85 D.85,85.5
12.函数的定义域为开区间,导函数在内的图象如下图所示,则函数在开区间内有极大值点( )
A.个 B .个 C .个 D .个
二、填空题(本大题共8小题,每小题5分,共40分,请将正确答案填空在答题卡上)
13.一支田径运动队有男运动员40人,女运动员30人. 现用分层抽样的方法抽取一个容量为35的样本,则抽取的女运动员有 人.21世纪教育网
14.抛掷一枚均匀的正方体骰子,点数为3的倍数的概率为 .
15.曲线在处的切线斜率为 .
16.以点(2,-1)为圆心,以3为半径的圆的标准方程是_____________________.
17.二进制数化为十进制数:____________(10).
18.双曲线的渐近线方程为________.
19.为了了解“预防禽流感疫苗”的使用情况,某市卫生部门对本地区5月份至7月份使用疫苗的所有养鸡场进行了调查,根据下列图表提供的信息,可以得出这三个月本地区平均每月注射了疫苗的鸡的数量为 万只.
20.函数的极小值是 .21世纪教育网
三、解答题(本大题共5小题,每题10分,共50分.请将详细解答过程写在答题卡上)
21.设:P: 指数函数在x∈R内单调递减;Q:.如果P为真,Q为假,求a的取值范围.
22.已知M={3,6,7,8},N={3,4,5},从M和N中各自任取一个数,分别记为和为,求≥11的概率.
23.从某学校高三年级800名学生中随机抽取50名测量身高,据测量被抽取的学生的身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组.第二组;…第八组,右图是按上述分组方法得到的条形图.
(1) 根据已知条件填写下面表格:
组别
1
2
3
4
5
6
7
8
样本数
2
4
10
1021世纪教育网
4
2
(2) 估计这所学校高三年级800名学生中身高在180cm以上(含180cm)的人数.
24.已知点A(-2,0),B(2,0),直线AP与直线AB相交于点P,它们的斜率之积为,求点P的轨迹方程(化为标准方程).
25.已知函数.
(1)求;(2)求函数的单调区间.21世纪教育网21世纪教育网
珠海市2012~2013学年度第一学期期末学生学业质量监测
高二文科数学试题(B卷)与参考答案
时量:120分钟 分值:150分. 内容:数学选修1-1和数学必修3.
一、选择题(本大题共12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的)
1.(逻辑)“”是“”的( )
A.充分而不必要条件 B 必要而不充分条件
C.充分必要条件 D .既不充分也不必要条件
2.(概率)抽查10件产品,设事件A:至少有两件次品,则与A的互斥的事件为( )
A.恰有两件次品 B.恰有一件次品 C.恰有两件正品 D.至少两件正品
3.(导数)已知函数,若,则
A. B. 或 C. D.
4.(圆锥曲线)椭圆的离心率等于( )
A. B . C . D .2
5.(圆锥曲线)抛物线的焦点坐标为 ( )
A . B . C . D.
6.(导数)下列求导运算正确的是 ( )
A . B .
C . D.21世纪教育网
7.(统计)如某校高中三年级的300名学生已经编号为0,1,……,299,为了了解学生的学习情况,要抽取一个样本数为60的样本,用系统抽样的方法进行抽取,若第60段所抽到的编号为298,则第1段抽到的编号为( )
A.2 B.3 C.4 D.5
8.(逻辑)已知命题:,则( )
A. B.
C. D.
9.(算法)下图是一个求和的程序框图,如果其中判断框内填入的条件是:?,那么输出S=( )
A. B. C. D.
10.(算法)下列程序的输出结果是( )
A.2,2
B.3,2
C.2,3
D.3,3
11.(统计)右图是2012年举行的全国少数民族运动会上,七位评委
为某民族舞蹈打出的分的茎叶统计图,去掉一个最高分和一个最低
分后,所剩数据的平均数和中位数分别为( )。
A.85,84 B.85,84.5 C.,85 D.,85.5
12.(导数)函数的定义域为开区间,导函数在内的图象如下图所示,则函数在开区间内有极大值点( )
A.个 B .个 C .个 D .个
二、填空题(本大题共8小题,每小题5分,共40分,请将正确答案填空在答题卡上)
13.(统计)一支田径运动队有男运动员40人,女运动员30人. 现用分层抽样的方法抽取一个容量为35的样本,则抽取的女运动员有 人.15
14.(概率)抛掷一枚均匀的正方体骰子,点数为3的倍数的概率为 .1/3
15.(导数)曲线在处的切线斜率为 2
16.(圆)以点(2,-1)为圆心,以3为半径的圆的标准方程是_____________________.
17.(算法)二进制数化为十进制数:____________(10).5
18.(圆锥曲线)双曲线的渐近线方程为________.
19.(统计)为了了解“预防禽流感疫苗”的使用情况,某市卫生部门对本地区5月份至7月份使用疫苗的所有养鸡场进行了调查,根据下列图表提供的信息,可以得出这三个月本地区平均每月注射了疫苗的鸡的数量为 万只.90
20.(导数)函数的极小值是 .
三、解答题(本大题共5小题,每题10分,共50分.请将详细解答过程写在答题卡上)21世纪教育网
21.(逻辑估级2.5)设:P: 指数函数在x∈R内单调递减;Q:。如果P为真,Q为假,求a的取值范围。
解:当0
由题意有P正确,且Q不正确,因此,a∈(0,1)∩…(8分)
即a∈…(10分)[来源:21世纪教育网]
22.(概率估级3)(本题满分10分) 21世纪教育网
已知M={3,6,7,8},N={3,4,5},从M和N中各自任取一个数,分别记为和为,求≥11的概率.
解:从M、N中各取一个数组成数对(x ,y),共有12对,…3分
其中满足的有:
(6,5),(7,4),(7,5),(8,3),(8,4),(8,5),共6对…6分[来源:21世纪教育网]
故所求概率为,所以使的概率为.…10分
23.(统计估级3)从某学校高三年级800名学生中随机抽取50名测量身高,据测量被抽取的学生的身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组.第二组;…第八组,右图是按上述分组方法得到的条形图.
(1) 根据已知条件填写下面表格:
组别
1
2
3
4
5
6
7
8
样本数
2
4
10
10
4
2
(2) 估计这所学校高三年级800名学生中身高在180cm以上(含180cm)的人数;
解: (Ⅰ)由条形图得第七组频率为
21世纪教育网
∴第七组的人数为3人……(2分)
0.3
∴第五组的人数为15人……(4分)
组别
1
2
3
4
5
6
7
8
样本中人数
2
4
10
10
15
4
3
2
(Ⅱ)由条形图得前五组频率为 (0.008+0.016+0.04+0.04+0.06)×5=0.82,
………………………………………6分
后三组频率为1-0.82=0.18 …………………………………8分
估计这所学校高三年级身高在180cm以上(含180cm)的人数:
800×0.18=144(人) …………………(10分)
24.(圆锥曲线估级4)已知点A(-2,0),B(2,0),直线AP与直线AB相交于点P,它们的斜率之积为,求点P的轨迹方程(化为标准方程).
解:设点P,21世纪教育网
直线AP的斜率…… (2分)
直线BP的斜率…… (4分)
根据已知,有:…… (7分)
化简得: ……… (10分)
(没有写扣1分)
25.(导数估级5)已知函数.
(1)求;(2)求函数的单调区间.
解:(1)∵,…… (2分)
∴…… (5分)
(2)∵
当时,也即当或时,单调递增;…… (7分)
当时,也即当时,单调递减;…… (9分)
∴函数的单调递增区间是和,单调递减区间是. (10分)
(在0,2处写成闭区间,也同样计分)
21世纪教育网
21世纪教育网
同课章节目录
