广东省珠海市2012-2013学年高二上学期期末质检数学理试题(B卷)
文档属性
| 名称 | 广东省珠海市2012-2013学年高二上学期期末质检数学理试题(B卷) |  | |
| 格式 | zip | ||
| 文件大小 | 223.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-25 14:45:48 | ||
图片预览




文档简介
珠海市2012~2013学年度第一学期期末学生学业质量监测
高二理科数学试题
时量:120分钟 分值:150分. 内容:圆,数学选修2-1和数学选修2-2.
一、选择题(本大题共12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的)
1.“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
若函数在区间上有,在区间上有,则
有( )
A.区间上单调递减,在区间上单调递增
B.区间上单调递减,在区间上单调递减
C.区间上单调递增,在区间上单调递增
D.区间上单调递增,在区间上单调递减
3.已知函数,若,则
A. B. 或 C. D.
4.椭圆的离心率等于( )21世纪教育网
A. B. C. D.2
5.抛物线的焦点坐标为 ( )
A. B. C. D.
6.下列求导运算正确的是 ( )
A. B.
C. D.
7.复数是纯虚数,则实数的值为
A.3 B.0 C.2 D.3或2
8.已知命题: ,则( )21世纪教育网
A. B.
C. D.
9.已知空间坐标系中,,, 是线段的中点,则点的坐标为
A. B. C. D.
10.已知,,则( )
A. B. C. D.
11.三角形的面积为为三角形的边长,r为三角形内切圆的半径,利用类比推理,可得出四面体的体积为( )
A.
B.
C. (分别为四面体的四个面的面积,r为四面体内切球的半径)
D.
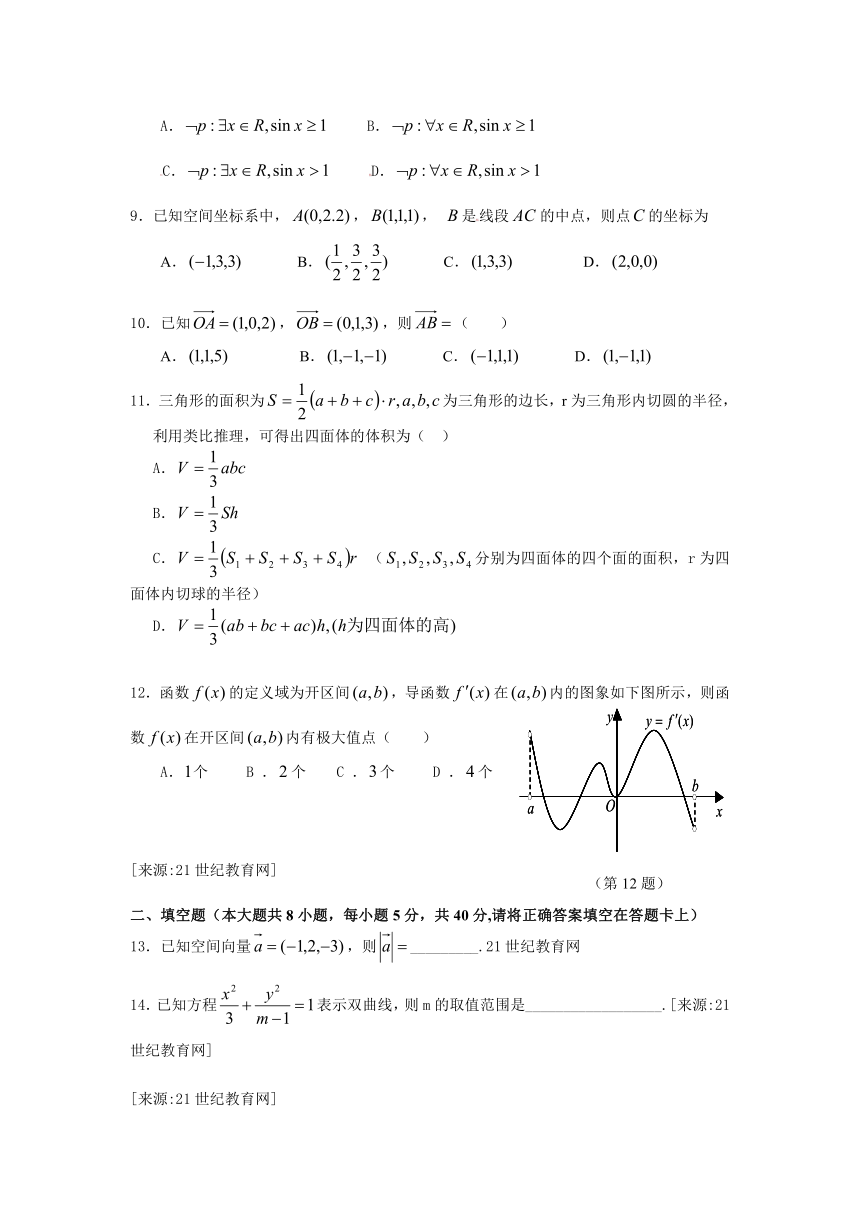
12.函数的定义域为开区间,导函数在内的图象如下图所示,则函数在开区间内有极大值点( )
A.个 B .个 C .个 D .个
[来源:21世纪教育网]
二、填空题(本大题共8小题,每小题5分,共40分,请将正确答案填空在答题卡上)
13.已知空间向量,则_________.21世纪教育网
14.已知方程表示双曲线,则m的取值范围是__________________.[来源:21世纪教育网]
[来源:21世纪教育网]
15.计算 .
16.以点(2,-1)为圆心,以3为半径的圆的标准方程是_____________________.
17.空间向量与所成的角为_________.
18.双曲线的渐近线方程为________.
19.设i是虚数单位,计算:_________.
20.函数的极小值是 .
三、解答题(本大题共5小题,每题10分,共50分.请将详细解答过程写在答题卡上)
21.设:P: 指数函数在x∈R内单调递减;Q:。如果P为真,Q为假,求a的取值范围.
22.已知抛物线,直线,求直线与抛物线的交点坐标.
21世纪教育网
23.如图,在长方体中,,。
(1)求证;
(2)求直线与平面所成角的正弦值.21世纪教育网
24.已知点A(-2,0),B(2,0),直线AP与直线AB相交于点P,它们的斜率之积为,求点P的轨迹方程(化为标准方程).
25.已知函数.
(1)求;(2)求函数的单调区间.
21世纪教育网
珠海市2012~2013学年度第一学期期末学生学业质量监测
高二理科数学试题(B卷)与参考答案
时量:120分钟 分值:150分. 内容:数学选修2-1和数学选修2-2.
一、选择题(本大题共12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的)
1.(逻辑)“”是“”的( )
A.充分而不必要条件 B. 必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
(导数)若函数在区间上有,在区间上有,则
有( )
A.区间上单调递减,在区间上单调递增
B.区间上单调递减,在区间上单调递减
C.区间上单调递增,在区间上单调递增
D.区间上单调递增,在区间上单调递减
3.(导数)已知函数,若,则珠海市2012-2013学年度第一学期期末考试
高二化学科试卷答案及评分标准
单项选择题(每题2分,共40分,20小题)
题号
1
2
3
4
5
6
7
8[21世纪教育网
9
10
11
12
13
14
15
16
17
18
19
20
答案
D
C
C
B
B
B
A
A
B
D
B
D
D
B
A
B
C
B
C
B
双项选择题(共15分,5小题,每小题3分,漏选且正确得2分,错选得0分)
题号
21
22
23
24
25
答案
AC
AB
BC
AB
AC
非选择题(共45分)
26、(共12分)
A、(1)1 (2)>(3)CH3COO-+H2OCH3COOH+OH- (4)C(每空2分)
B、Cu(OH)2 (2分) Cu2++2NH3·H2O = Cu(OH)2↓ +2NH4+ (2分)21世纪教育网
27、(共8分)21世纪教育网
①增大 ②增大 ③减小 ④不变(各2分,共8分)
28、(共15分)
(1)1000mL容量瓶(2分) ,胶头滴管(2分)
(2)①酸式(2分) ②锥形瓶内溶液颜色的变化(2分)
(3)①无影响 ②偏高 ③偏小 ④偏高 (每空1分)
(4)80.8%(3分)
29、(共10分)(每空2分)21世纪教育网
(1)放; (2)K=C2(NO2)/C2(NO)C(O2) (3)b; 0.0015mol/(L·s); (4)c
A. B. 或 C. D.
4.(圆锥曲线)椭圆的离心率等于( )珠海市2012-2013学年度第一学期期末考试
高二化学科试卷答案及评分标准
单项选择题(每题2分,共40分,20小题)
题号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
答案
D
C
C
B
B
B
A
A
B
D
B
D
D
B
A
B
C
B
C
B
双项选择题(共15分,5小题,每小题3分,漏选且正确得2分,错选得0分)
题号
21
22
2321世纪教育网
24
25
答案
AC
AB
BC
AB
AC
非选择题(共45分)
26、(共12分)
A、(1)1 (2)>(3)CH3COO-+H2OCH3COOH+OH- (4)C(每空2分)
B、Cu(OH)2 (2分) Cu2++2NH3·H2O = Cu(OH)2↓ +2NH4+ (2分)
27、(共8分)21世纪教育网
①增大 ②增大 ③减小 ④不变(各2分,共8分)
28、(共15分)
(1)1000mL容量瓶(2分) ,胶头滴管(2分)
(2)①酸式(2分) ②锥形瓶内溶液颜色的变化(2分)
(3)①无影响 ②偏高 ③偏小 ④偏高 (每空1分)
(4)80.8%(3分)
29、(共10分)(每空2分)21世纪教育网
(1)放; (2)K=C2(NO2)/C2(NO)C(O2) (3)b; 0.0015mol/(L·s); (4)c
A. B. C. D.2
5.(圆锥曲线)抛物线的焦点坐标为 ( )
A. B. C. D.
6.(导数)下列求导运算正确的是 ( )
A. B.
C. D.
7.(复数)复数是纯虚数,则实数的值为
A.3 B.0 C.2 D.3或2
8.(逻辑)已知命题:,则( )
A. B.
C. D.
9.(空间向量)已知空间坐标系中,,,是线段的中点,则点的坐标为
A. B. C. D.
10.已知,,则( )
A. B. C. D.
11.(推理)三角形的面积为为三角形的边长,r为三角形内切圆的半径,利用类比推理,可得出四面体的体积为( )
A.
B.
C. (分别为四面体的四个面的面积,r为四面体内切球的半径)
D.
12.(导数)函数的定义域为开区间,导函数在内的图象如下图所示,则函数在开区间内有极大值点( )
A.个 B .个 C .个 D .个
二、填空题(本大题共8小题,每小题5分,共40分,请将正确答案填空在答题卡上)
13.(空间向量)已知空间向量,则_________.
14.(圆锥曲线)已知方程表示双曲线,则m的取值范围是__________________.
15.(导数)计算 .10
16.(圆)以点(2,-1)为圆心,以3为半径的圆的标准方程是_____________________.21世纪教育网
17.空间向量与所成的角为_________.
18.(圆锥曲线)双曲线的渐近线方程为________.
19.(复数)设i是虚数单位,计算:_________.
20.(导数)函数的极小值是 .
三、解答题(本大题共5小题,每题10分,共50分.请将详细解答过程写在答题卡上)
21.(逻辑估级2.5)设:P: 指数函数在x∈R内单调递减;Q:。如果P为真,Q为假,求a的取值范围。
解:当0 ∴P为真时,0∵Q为假, ∴…(5分)
由题意有P正确,且Q不正确,因此,a∈(0,1)∩…(8分)
即a∈…(10分)
(圆锥曲线估级3)已知抛物线,直线,求直线与抛物线的交点坐标。
解:联立方程得……(2分)
将(2)代入(1)得:,化简得:……(4分)
解得:……(7分)
代入(2)得:……(8分)
∴或……(9分)
直线与抛物线的交点坐标为或。……(10分)
23.(空间向量)如图,在长方体中,,。
(1)求证;
(2)求直线与平面所成角的正弦值.
解:(1)如图,以D为原点,以DC直线为Y轴,以DA直线为Z轴,建立空间直角坐标系。
则…(2分)21世纪教育网
,,…(3分)
,…(4分)
∴…(5分)
(2)∵,…
∴,…(7分)
,
∴是平面的法向量…(8分)
∴与所成角的余弦值的绝对值等于直线与平面所成角的正弦值,
.…(9分)
直线与平面所成角的正弦值为.…(10分)
24.(圆锥曲线估级4)已知点A(-2,0),B(2,0),直线AP与直线AB相交于点P,它们的斜率之积为,求点P的轨迹方程(化为标准方程).[来源:21世纪教育网]
解:设点P,
直线AP的斜率…… (2分)
直线BP的斜率…… (4分)
根据已知,有:…… (7分)
化简得: ……… (10分)
(没有写扣1分)
25.(导数估级5)已知函数.
(1)求;(2)求函数的单调区间.
解:(1)∵,…… (2分)
∴…… (5分)
(2)∵
当时,也即当或时,单调递增;…… (7分)
当时,也即当时,单调递减;…… (9分)
∴函数的单调递增区间是和,单调递减区间是. (10分)
(在0,2处写成闭区间,也同样计分)
21世纪教育网
高二理科数学试题
时量:120分钟 分值:150分. 内容:圆,数学选修2-1和数学选修2-2.
一、选择题(本大题共12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的)
1.“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
若函数在区间上有,在区间上有,则
有( )
A.区间上单调递减,在区间上单调递增
B.区间上单调递减,在区间上单调递减
C.区间上单调递增,在区间上单调递增
D.区间上单调递增,在区间上单调递减
3.已知函数,若,则
A. B. 或 C. D.
4.椭圆的离心率等于( )21世纪教育网
A. B. C. D.2
5.抛物线的焦点坐标为 ( )
A. B. C. D.
6.下列求导运算正确的是 ( )
A. B.
C. D.
7.复数是纯虚数,则实数的值为
A.3 B.0 C.2 D.3或2
8.已知命题: ,则( )21世纪教育网
A. B.
C. D.
9.已知空间坐标系中,,, 是线段的中点,则点的坐标为
A. B. C. D.
10.已知,,则( )
A. B. C. D.
11.三角形的面积为为三角形的边长,r为三角形内切圆的半径,利用类比推理,可得出四面体的体积为( )
A.
B.
C. (分别为四面体的四个面的面积,r为四面体内切球的半径)
D.
12.函数的定义域为开区间,导函数在内的图象如下图所示,则函数在开区间内有极大值点( )
A.个 B .个 C .个 D .个
[来源:21世纪教育网]
二、填空题(本大题共8小题,每小题5分,共40分,请将正确答案填空在答题卡上)
13.已知空间向量,则_________.21世纪教育网
14.已知方程表示双曲线,则m的取值范围是__________________.[来源:21世纪教育网]
[来源:21世纪教育网]
15.计算 .
16.以点(2,-1)为圆心,以3为半径的圆的标准方程是_____________________.
17.空间向量与所成的角为_________.
18.双曲线的渐近线方程为________.
19.设i是虚数单位,计算:_________.
20.函数的极小值是 .
三、解答题(本大题共5小题,每题10分,共50分.请将详细解答过程写在答题卡上)
21.设:P: 指数函数在x∈R内单调递减;Q:。如果P为真,Q为假,求a的取值范围.
22.已知抛物线,直线,求直线与抛物线的交点坐标.
21世纪教育网
23.如图,在长方体中,,。
(1)求证;
(2)求直线与平面所成角的正弦值.21世纪教育网
24.已知点A(-2,0),B(2,0),直线AP与直线AB相交于点P,它们的斜率之积为,求点P的轨迹方程(化为标准方程).
25.已知函数.
(1)求;(2)求函数的单调区间.
21世纪教育网
珠海市2012~2013学年度第一学期期末学生学业质量监测
高二理科数学试题(B卷)与参考答案
时量:120分钟 分值:150分. 内容:数学选修2-1和数学选修2-2.
一、选择题(本大题共12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的)
1.(逻辑)“”是“”的( )
A.充分而不必要条件 B. 必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
(导数)若函数在区间上有,在区间上有,则
有( )
A.区间上单调递减,在区间上单调递增
B.区间上单调递减,在区间上单调递减
C.区间上单调递增,在区间上单调递增
D.区间上单调递增,在区间上单调递减
3.(导数)已知函数,若,则珠海市2012-2013学年度第一学期期末考试
高二化学科试卷答案及评分标准
单项选择题(每题2分,共40分,20小题)
题号
1
2
3
4
5
6
7
8[21世纪教育网
9
10
11
12
13
14
15
16
17
18
19
20
答案
D
C
C
B
B
B
A
A
B
D
B
D
D
B
A
B
C
B
C
B
双项选择题(共15分,5小题,每小题3分,漏选且正确得2分,错选得0分)
题号
21
22
23
24
25
答案
AC
AB
BC
AB
AC
非选择题(共45分)
26、(共12分)
A、(1)1 (2)>(3)CH3COO-+H2OCH3COOH+OH- (4)C(每空2分)
B、Cu(OH)2 (2分) Cu2++2NH3·H2O = Cu(OH)2↓ +2NH4+ (2分)21世纪教育网
27、(共8分)21世纪教育网
①增大 ②增大 ③减小 ④不变(各2分,共8分)
28、(共15分)
(1)1000mL容量瓶(2分) ,胶头滴管(2分)
(2)①酸式(2分) ②锥形瓶内溶液颜色的变化(2分)
(3)①无影响 ②偏高 ③偏小 ④偏高 (每空1分)
(4)80.8%(3分)
29、(共10分)(每空2分)21世纪教育网
(1)放; (2)K=C2(NO2)/C2(NO)C(O2) (3)b; 0.0015mol/(L·s); (4)c
A. B. 或 C. D.
4.(圆锥曲线)椭圆的离心率等于( )珠海市2012-2013学年度第一学期期末考试
高二化学科试卷答案及评分标准
单项选择题(每题2分,共40分,20小题)
题号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
答案
D
C
C
B
B
B
A
A
B
D
B
D
D
B
A
B
C
B
C
B
双项选择题(共15分,5小题,每小题3分,漏选且正确得2分,错选得0分)
题号
21
22
2321世纪教育网
24
25
答案
AC
AB
BC
AB
AC
非选择题(共45分)
26、(共12分)
A、(1)1 (2)>(3)CH3COO-+H2OCH3COOH+OH- (4)C(每空2分)
B、Cu(OH)2 (2分) Cu2++2NH3·H2O = Cu(OH)2↓ +2NH4+ (2分)
27、(共8分)21世纪教育网
①增大 ②增大 ③减小 ④不变(各2分,共8分)
28、(共15分)
(1)1000mL容量瓶(2分) ,胶头滴管(2分)
(2)①酸式(2分) ②锥形瓶内溶液颜色的变化(2分)
(3)①无影响 ②偏高 ③偏小 ④偏高 (每空1分)
(4)80.8%(3分)
29、(共10分)(每空2分)21世纪教育网
(1)放; (2)K=C2(NO2)/C2(NO)C(O2) (3)b; 0.0015mol/(L·s); (4)c
A. B. C. D.2
5.(圆锥曲线)抛物线的焦点坐标为 ( )
A. B. C. D.
6.(导数)下列求导运算正确的是 ( )
A. B.
C. D.
7.(复数)复数是纯虚数,则实数的值为
A.3 B.0 C.2 D.3或2
8.(逻辑)已知命题:,则( )
A. B.
C. D.
9.(空间向量)已知空间坐标系中,,,是线段的中点,则点的坐标为
A. B. C. D.
10.已知,,则( )
A. B. C. D.
11.(推理)三角形的面积为为三角形的边长,r为三角形内切圆的半径,利用类比推理,可得出四面体的体积为( )
A.
B.
C. (分别为四面体的四个面的面积,r为四面体内切球的半径)
D.
12.(导数)函数的定义域为开区间,导函数在内的图象如下图所示,则函数在开区间内有极大值点( )
A.个 B .个 C .个 D .个
二、填空题(本大题共8小题,每小题5分,共40分,请将正确答案填空在答题卡上)
13.(空间向量)已知空间向量,则_________.
14.(圆锥曲线)已知方程表示双曲线,则m的取值范围是__________________.
15.(导数)计算 .10
16.(圆)以点(2,-1)为圆心,以3为半径的圆的标准方程是_____________________.21世纪教育网
17.空间向量与所成的角为_________.
18.(圆锥曲线)双曲线的渐近线方程为________.
19.(复数)设i是虚数单位,计算:_________.
20.(导数)函数的极小值是 .
三、解答题(本大题共5小题,每题10分,共50分.请将详细解答过程写在答题卡上)
21.(逻辑估级2.5)设:P: 指数函数在x∈R内单调递减;Q:。如果P为真,Q为假,求a的取值范围。
解:当0
由题意有P正确,且Q不正确,因此,a∈(0,1)∩…(8分)
即a∈…(10分)
(圆锥曲线估级3)已知抛物线,直线,求直线与抛物线的交点坐标。
解:联立方程得……(2分)
将(2)代入(1)得:,化简得:……(4分)
解得:……(7分)
代入(2)得:……(8分)
∴或……(9分)
直线与抛物线的交点坐标为或。……(10分)
23.(空间向量)如图,在长方体中,,。
(1)求证;
(2)求直线与平面所成角的正弦值.
解:(1)如图,以D为原点,以DC直线为Y轴,以DA直线为Z轴,建立空间直角坐标系。
则…(2分)21世纪教育网
,,…(3分)
,…(4分)
∴…(5分)
(2)∵,…
∴,…(7分)
,
∴是平面的法向量…(8分)
∴与所成角的余弦值的绝对值等于直线与平面所成角的正弦值,
.…(9分)
直线与平面所成角的正弦值为.…(10分)
24.(圆锥曲线估级4)已知点A(-2,0),B(2,0),直线AP与直线AB相交于点P,它们的斜率之积为,求点P的轨迹方程(化为标准方程).[来源:21世纪教育网]
解:设点P,
直线AP的斜率…… (2分)
直线BP的斜率…… (4分)
根据已知,有:…… (7分)
化简得: ……… (10分)
(没有写扣1分)
25.(导数估级5)已知函数.
(1)求;(2)求函数的单调区间.
解:(1)∵,…… (2分)
∴…… (5分)
(2)∵
当时,也即当或时,单调递增;…… (7分)
当时,也即当时,单调递减;…… (9分)
∴函数的单调递增区间是和,单调递减区间是. (10分)
(在0,2处写成闭区间,也同样计分)
21世纪教育网
同课章节目录
