人教版四年级下册数学 5.3三角形内角和 教案
文档属性
| 名称 | 人教版四年级下册数学 5.3三角形内角和 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 540.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-04 10:59:12 | ||
图片预览


文档简介
人教版小学数学四年级下册《三角形内角和》教学设计
教学目标:
1、通过测量、撕拼、折叠等方法,探索并发现三角形内角和是 180°的规律。
2、在探究过程中,经历知识产生、发展和变化过程,通过交流比较,培养策略意识和初步的空间思维能力。
3、体验探究的过程和方法,感受思维提升的过程,激发求知欲和探索兴趣。
重点:
探究发现和验证“三角形内角和 180度”这一规律的过程,并归纳总结出规律。
难点:
对不同探究方法的指导和学生对规律的应用。
教具学具准备:
学生三角尺,不同形状的三角形,量角器,多媒体课件,教师三角尺 (分组,选组长,明确分工,记录单)。
教法学法:
小组合作、探究学习法
教学过程
课前交流:
孩子们,这节课我们以小组比赛的形式进行,比一比哪个小组表现最出色!上课之前咱们先做个手指操放松一下。
师:最后一个手势是个什么图形?
生:三角形
师:这节课我们就一起走进三角形王国继续学习和三角形有关的知识。上课!
一、创设情境,生成问题。
师:说起三角形,老师想考考大家,三角形按角分可以分成几类?分别是?
生:3类,分别是直角三角形、锐角三角形、钝角三角形。
师:上节课的知识掌握的真不错!现在有请三角形三兄弟闪亮登场。
生 1:大家好,我是直角三角形,我的个头最大,我的内角和最大!
生 2:大家好,我是锐角三角形,我的个头最小,我的内角和最小......
生 3:大家好,我是钝角三角形,我的钝角比你们每个内角都大,我的内角和才是最大的!
师:同学们,你们同意他们的说法吗?
生:不同意,他们的内角和是一样大的,都是 180度。
师:他们的内角和都是 180度吗?这只是我们的猜想,板贴“猜想”。这节课我们就一起研究三角形的内角和。板书课题:三角形的内角和
二、探索交流,解决问题
1、分组验证不同三角形的内角和有了猜想就成功了一半,接下来我们就分组验证三角形的内角和到底是不是 180度!请看分工要求:拿出学具包,先讨论方法,再分工安排用不同的的方法推导三角形的内角和。1组 2组研究讨论锐角三角形的内角和。3组 4组研究讨论直角三角形的内角和。5组 6组研究讨论钝角三角形的内角和。
2、全班汇报交流锐角三角形:
生 1:我们用了量一量的方法,分别测出三个内角的度数,然后求和,我们组的结论是:三角形的内角和大约是 180度。我的汇报完毕,谁还有补充?
生 2:我们用了撕一撕的方法,先将三个内角撕下来,然后拼在一起刚好组成一个平角。所以我们的结论是三角形的内角和是 180度。我的汇报完毕,谁还有疑问或补充?
生 3:我们用了折一折的方法,也折成一个平角,因此我们的结论也是三角形的内角和是 180度。
请 2其同学对前两个小组的汇报点评。
直角三角形:三名同学汇报量、撕、折的方法。
师:除了这三种方法,还有不同的方法可以证明直角三角形的内角和是 180度吗?
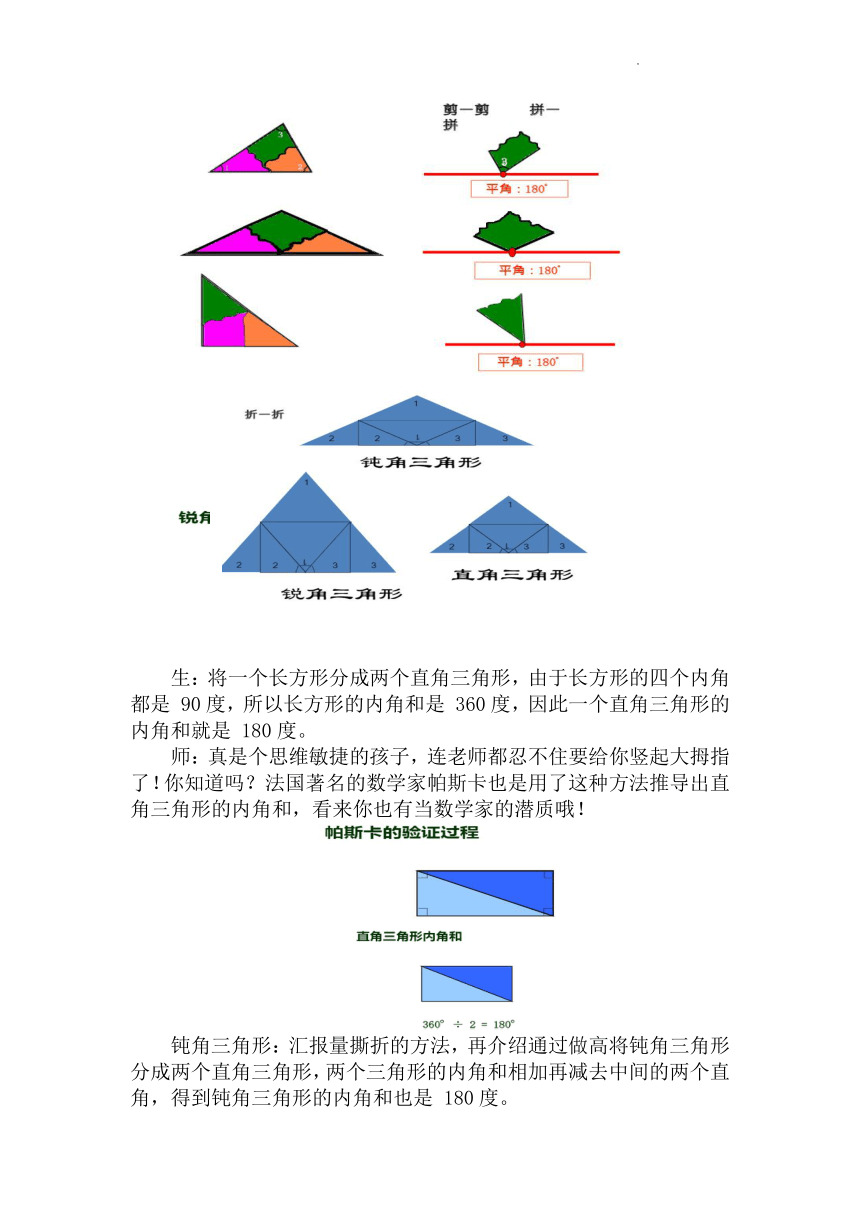
生:将一个长方形分成两个直角三角形,由于长方形的四个内角都是 90度,所以长方形的内角和是 360度,因此一个直角三角形的内角和就是 180度。
师:真是个思维敏捷的孩子,连老师都忍不住要给你竖起大拇指了!你知道吗?法国著名的数学家帕斯卡也是用了这种方法推导出直角三角形的内角和,看来你也有当数学家的潜质哦!
钝角三角形:汇报量撕折的方法,再介绍通过做高将钝角三角形分成两个直角三角形,两个三角形的内角和相加再减去中间的两个直角,得到钝角三角形的内角和也是 180度。
师:团结的力量可真大,为了便于观察,老师把同学们的方法请到大屏幕上,请看!通过对这三兄弟内角和的研究,你得到了什么结论?
生:三角形的内角和是 180度。
板书:三角形的内角和是 180度。不管是帕斯卡的方法还是剪一剪折一折的方法,都用到了一种重要的数学思想方法——转化,这种方法很重要,同学们可要牢牢掌握哦!
三、巩固应用,内化提高
既然我们已经知道三角形的内角和是 180度,接下来电脑博士要考考大家。
1、看图,算出笑脸所遮盖角的度数。
180 °— 80 °— 30 °=70 °180 °— 40 °— 20 °=120 °
2、猜猜三角形的各个角的度数
3、把下面这个三角形沿虚线剪成两个小三角形,每个小三角形的内角和是多少度?
答:每个小三角形的内角和仍是180 °
四、回顾整理,反思提升全课总结
同学们回顾一下我们今天所学的知识,你有什么收获啊。
结论:所有的三角形内角和都是180°
课后反思
《三角形的内角和》在学生学习了三角形的特征以及三角形分类的基础上,进一步研究三角形三个角的关系。让学生猜测-质疑-验证得出“三角形的内角和等于 180°”,引导学生观察、实验、猜测,逐步培养学生的逻辑推理能力。 我设计验证过程让学生分三大组分别研究锐角三角形、直角三角形和钝角三角形,鼓励学生通过不同方法研究,通过量一量、算一算、折一折、撕一撕、拼一拼的方法让学生验证各类三角形的内角和,一是加深对三角形内角和的理解就是三个内角的度数之和,二是让学生在小组内通过动手操作、记录、观察,验证三角形的内角和是否为 180°。我这样设计是为了让每一组的研究更具有针对性,达到由小组交流合作上升到全班合作,但也导致有些同学没有对其它两个种类三角形进行实际操作,应该布置孩子课下根据本节课的学习再熟悉其它两类三角形内角和的探讨。 探究新知是为了应用,这节课在练习的安排上,我注意把握练习层次,共安排三个层次,由易到难,逐步加深。第一层练习是已知两角度数求第三个角的度数,让学生应用结论思考分析,检验语言的严密性。第二层练习是特殊三角形中,求另一个角。练习内容的安排从知识的直接应用到间接应用,数学信息的出现从比较显现到较为隐藏。最后设置综合性较强题目。 本节课我采用逐步设置疑问,让学生动手、动脑、动口,积极参与知识学习的全过程,渗透多观察、动脑想、大胆猜、勤钻研的研讨式学习方法,培养学生学习数学的兴趣,给学生提供更多的活动机会和空间,使学生在参与的过程中得到充足的体验和发展。
教学目标:
1、通过测量、撕拼、折叠等方法,探索并发现三角形内角和是 180°的规律。
2、在探究过程中,经历知识产生、发展和变化过程,通过交流比较,培养策略意识和初步的空间思维能力。
3、体验探究的过程和方法,感受思维提升的过程,激发求知欲和探索兴趣。
重点:
探究发现和验证“三角形内角和 180度”这一规律的过程,并归纳总结出规律。
难点:
对不同探究方法的指导和学生对规律的应用。
教具学具准备:
学生三角尺,不同形状的三角形,量角器,多媒体课件,教师三角尺 (分组,选组长,明确分工,记录单)。
教法学法:
小组合作、探究学习法
教学过程
课前交流:
孩子们,这节课我们以小组比赛的形式进行,比一比哪个小组表现最出色!上课之前咱们先做个手指操放松一下。
师:最后一个手势是个什么图形?
生:三角形
师:这节课我们就一起走进三角形王国继续学习和三角形有关的知识。上课!
一、创设情境,生成问题。
师:说起三角形,老师想考考大家,三角形按角分可以分成几类?分别是?
生:3类,分别是直角三角形、锐角三角形、钝角三角形。
师:上节课的知识掌握的真不错!现在有请三角形三兄弟闪亮登场。
生 1:大家好,我是直角三角形,我的个头最大,我的内角和最大!
生 2:大家好,我是锐角三角形,我的个头最小,我的内角和最小......
生 3:大家好,我是钝角三角形,我的钝角比你们每个内角都大,我的内角和才是最大的!
师:同学们,你们同意他们的说法吗?
生:不同意,他们的内角和是一样大的,都是 180度。
师:他们的内角和都是 180度吗?这只是我们的猜想,板贴“猜想”。这节课我们就一起研究三角形的内角和。板书课题:三角形的内角和
二、探索交流,解决问题
1、分组验证不同三角形的内角和有了猜想就成功了一半,接下来我们就分组验证三角形的内角和到底是不是 180度!请看分工要求:拿出学具包,先讨论方法,再分工安排用不同的的方法推导三角形的内角和。1组 2组研究讨论锐角三角形的内角和。3组 4组研究讨论直角三角形的内角和。5组 6组研究讨论钝角三角形的内角和。
2、全班汇报交流锐角三角形:
生 1:我们用了量一量的方法,分别测出三个内角的度数,然后求和,我们组的结论是:三角形的内角和大约是 180度。我的汇报完毕,谁还有补充?
生 2:我们用了撕一撕的方法,先将三个内角撕下来,然后拼在一起刚好组成一个平角。所以我们的结论是三角形的内角和是 180度。我的汇报完毕,谁还有疑问或补充?
生 3:我们用了折一折的方法,也折成一个平角,因此我们的结论也是三角形的内角和是 180度。
请 2其同学对前两个小组的汇报点评。
直角三角形:三名同学汇报量、撕、折的方法。
师:除了这三种方法,还有不同的方法可以证明直角三角形的内角和是 180度吗?
生:将一个长方形分成两个直角三角形,由于长方形的四个内角都是 90度,所以长方形的内角和是 360度,因此一个直角三角形的内角和就是 180度。
师:真是个思维敏捷的孩子,连老师都忍不住要给你竖起大拇指了!你知道吗?法国著名的数学家帕斯卡也是用了这种方法推导出直角三角形的内角和,看来你也有当数学家的潜质哦!
钝角三角形:汇报量撕折的方法,再介绍通过做高将钝角三角形分成两个直角三角形,两个三角形的内角和相加再减去中间的两个直角,得到钝角三角形的内角和也是 180度。
师:团结的力量可真大,为了便于观察,老师把同学们的方法请到大屏幕上,请看!通过对这三兄弟内角和的研究,你得到了什么结论?
生:三角形的内角和是 180度。
板书:三角形的内角和是 180度。不管是帕斯卡的方法还是剪一剪折一折的方法,都用到了一种重要的数学思想方法——转化,这种方法很重要,同学们可要牢牢掌握哦!
三、巩固应用,内化提高
既然我们已经知道三角形的内角和是 180度,接下来电脑博士要考考大家。
1、看图,算出笑脸所遮盖角的度数。
180 °— 80 °— 30 °=70 °180 °— 40 °— 20 °=120 °
2、猜猜三角形的各个角的度数
3、把下面这个三角形沿虚线剪成两个小三角形,每个小三角形的内角和是多少度?
答:每个小三角形的内角和仍是180 °
四、回顾整理,反思提升全课总结
同学们回顾一下我们今天所学的知识,你有什么收获啊。
结论:所有的三角形内角和都是180°
课后反思
《三角形的内角和》在学生学习了三角形的特征以及三角形分类的基础上,进一步研究三角形三个角的关系。让学生猜测-质疑-验证得出“三角形的内角和等于 180°”,引导学生观察、实验、猜测,逐步培养学生的逻辑推理能力。 我设计验证过程让学生分三大组分别研究锐角三角形、直角三角形和钝角三角形,鼓励学生通过不同方法研究,通过量一量、算一算、折一折、撕一撕、拼一拼的方法让学生验证各类三角形的内角和,一是加深对三角形内角和的理解就是三个内角的度数之和,二是让学生在小组内通过动手操作、记录、观察,验证三角形的内角和是否为 180°。我这样设计是为了让每一组的研究更具有针对性,达到由小组交流合作上升到全班合作,但也导致有些同学没有对其它两个种类三角形进行实际操作,应该布置孩子课下根据本节课的学习再熟悉其它两类三角形内角和的探讨。 探究新知是为了应用,这节课在练习的安排上,我注意把握练习层次,共安排三个层次,由易到难,逐步加深。第一层练习是已知两角度数求第三个角的度数,让学生应用结论思考分析,检验语言的严密性。第二层练习是特殊三角形中,求另一个角。练习内容的安排从知识的直接应用到间接应用,数学信息的出现从比较显现到较为隐藏。最后设置综合性较强题目。 本节课我采用逐步设置疑问,让学生动手、动脑、动口,积极参与知识学习的全过程,渗透多观察、动脑想、大胆猜、勤钻研的研讨式学习方法,培养学生学习数学的兴趣,给学生提供更多的活动机会和空间,使学生在参与的过程中得到充足的体验和发展。
