上海市徐汇区2013年中考一模(即期末)数学试题
文档属性
| 名称 | 上海市徐汇区2013年中考一模(即期末)数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 212.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-25 18:19:43 | ||
图片预览


文档简介
2012学年第一学期徐汇区初三年级数学学科
期终学习能力诊断卷 2013、1
(时间100分钟 满分150分)
考生注意∶
1.本试卷含三个大题,共25题;答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;
2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.
一.选择题(本大题共6题,每题4分,满分24分)
【下列各题的四个选项中,有且只有一个选项是正确的】
1.在中,,,,那么等于…………( )
A.; B..; C.; D..
2.将抛物线沿轴向上平移1个单位后所得抛物线的解析式是 …………( )
A.; B.; C.; D..
3.坡比等于1∶的斜坡的坡角等于 ………………………………………………( )
A.; B.; C.; D..
4.关于二次函数的图像,下列说法正确的是…………………………( ).
A.开口向下; B.最低点是;
C.对称轴是直线; D.对称轴的右侧部分是上升的.
5.如图1,相交于点,下列条件中能判定∥的是 …………( )
A.; B.;
C.; D..
6.如图2,在中,,垂足为,那么下列结论中错误的
是………………………………………………………………………………………( )
A.; B.;
C.; D..
二.填空题(本大题共12题,每题4分,满分48分)
7.计算: ▲ .
8.计算: ▲ .
9.抛物线与轴的交点坐标是 ▲ .
10.如果两个相似三角形对应角平分线的比是,那么它们对应高的比是 ▲ .
11.如图3,已知∥∥,,,那么 ▲ .
12.点是线段上一点,,点分别是线段的中点,那么
等于 ▲ .
13.抛物线过和两点 ,那么该抛物线的对称轴是 ▲ .
14.在以O为坐标原点的直角坐标平面内有一点A(2,4),如果AO与x轴正半轴的夹角
为,那么= .
15.小明同学身高1.5米,经太阳光照射,在地面的影长为2米,他此时测得旗杆在同一地
面的影长为12米,那么旗杆高为 __ ▲ 米.
16.抛物线与x轴交于点(点在点的左侧),与轴交于点,且,,那么的值是 ▲ .
17.两个等腰直角三角形和的位置如图4所示,
点和点分别在一直线上,,
,,点分别是、
的重心,联结,那么 ▲ .
18.在中,,,,点是斜边AB的中点,把绕点旋转,使得点落在射线上,点落在点.那么的长是_____▲________.
三.(本大题共7题,第19—22题每题10分;第23、24题每题12分;第25题14分;
满分78分)
19.(本题满分10分)
抛物线经过点、两点.
(1)求抛物线顶点的坐标; (5分)
(2)抛物线与轴的另一交点为,求的面积. (5分)
20.(本题满分10分)
如图5,在中,点是边的中点,,.
(1)求的长; (5分)
(2)设,=,求向量(用向量、表示). (5分)
21.(本题满分10分)
如图6,在中,平分交于点,过点作∥交于
点.
(1)求证:; (5分)
(2)如果,,,求的长. (5分)
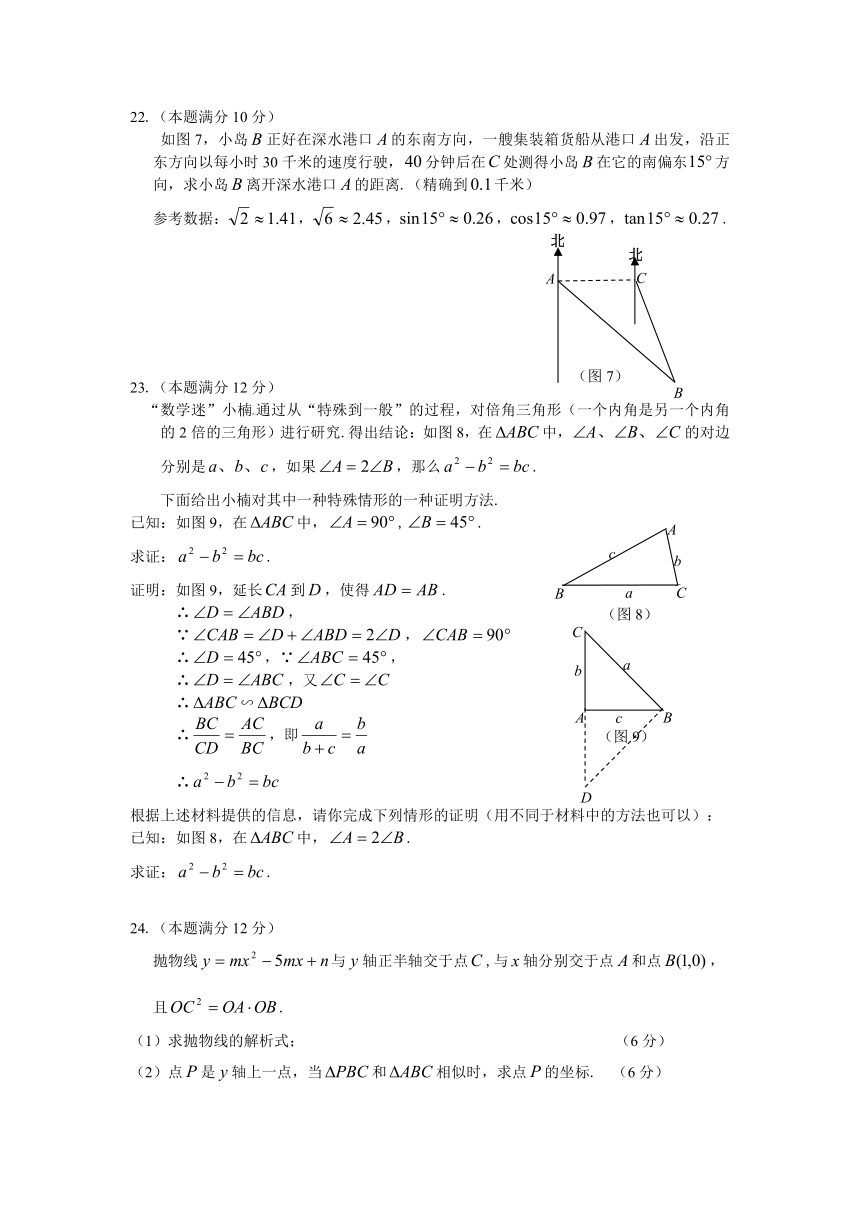
22.(本题满分10分)
如图7,小岛正好在深水港口的东南方向,一艘集装箱货船从港口出发,沿正东方向以每小时30千米的速度行驶,分钟后在处测得小岛在它的南偏东方向,求小岛离开深水港口的距离.(精确到千米)
参考数据:,,,,.
23.(本题满分12分)
“数学迷”小楠通过从“特殊到一般”的过程,对倍角三角形(一个内角是另一个内角的2倍的三角形)进行研究.得出结论:如图8,在中,的对边分别是,如果,那么.
下面给出小楠对其中一种特殊情形的一种证明方法.
已知:如图9,在中,,.
求证:.
证明:如图9,延长到,使得.
∴,
∵,
∴,∵,
∴,又
∴∽
∴,即
∴
根据上述材料提供的信息,请你完成下列情形的证明(用不同于材料中的方法也可以):
已知:如图8,在中,.
求证:.
24.(本题满分12分)
抛物线与轴正半轴交于点,与轴分别交于点和点,
且.
(1)求抛物线的解析式; (6分)
(2)点是轴上一点,当和相似时,求点的坐标. (6分)
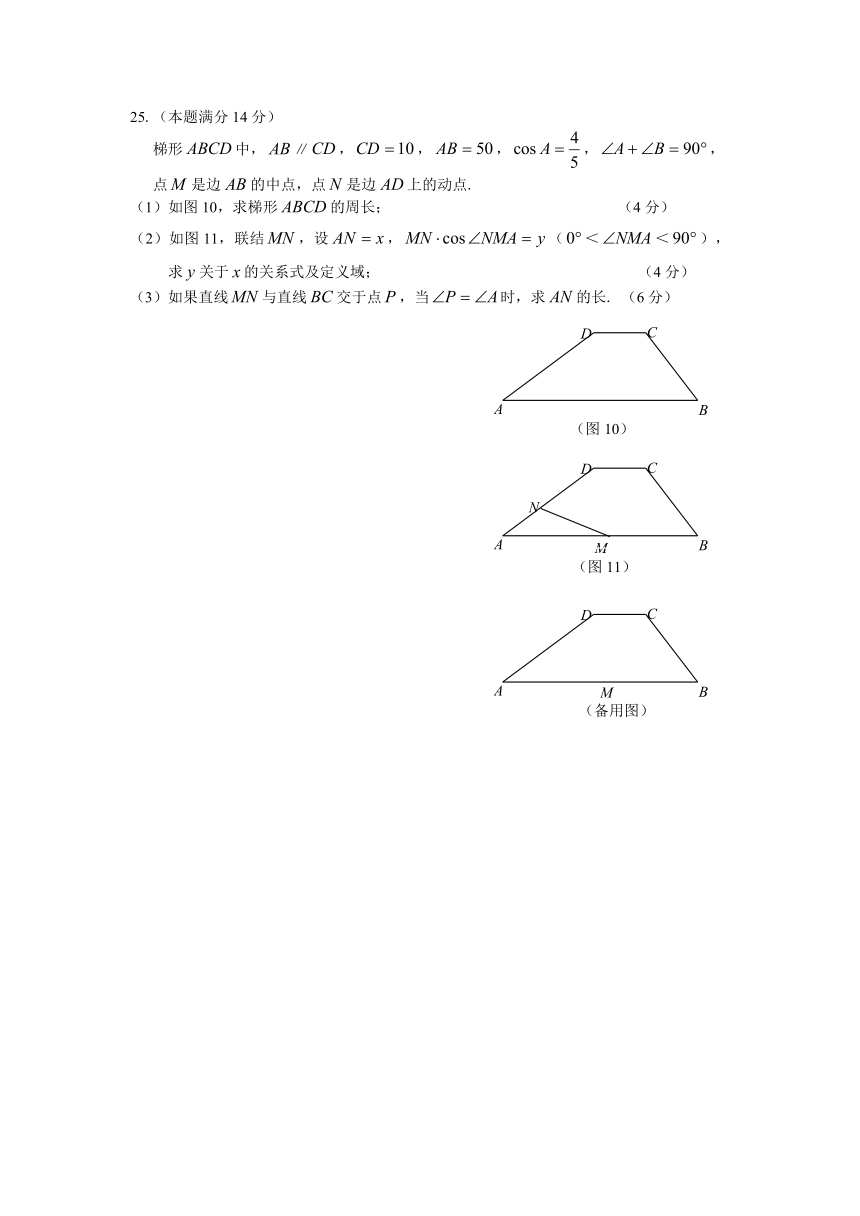
25.(本题满分14分)
梯形中,∥,,,,,
点是边的中点,点是边上的动点.
(1)如图10,求梯形的周长; (4分)
(2)如图11,联结,设,(<<),求关于的关系式及定义域; (4分)
(3)如果直线与直线交于点,当时,求的长. (6分)
2012学年第一学期徐汇区初三年级数学学科
期终学习能力诊断卷参考答案和评分标准
一、选择题:(本大题共6题,每题4分,满分24分)
1.C; 2.B; 3.A; 4.D; 5.D; 6.B.
二.填空题:(本大题共12题,满分48分)
7.; 8.; 9.; 10.; 11.; 12.(或);
13.直线; 14.; 15.; 16.或; 17.(或); 18..
三、(本大题共7题,第19、20、21、22题每题10分,第23、24题每题12分,第25题14分,满分78分)
19. 解:(1)由题意,得………………………………………(1分)
解得………………………………………………………(1分)
∴………………………………………………(1分)
∴……………………………………………………………(2分)
(2)由题意,得,解得;
∴ …………………………………………………………(2分)
又、
∴ …………………………………………(3分)
20.解:(1)∵点是边的中点,,∴(1分)
∴,………………………………(1分)
∴,又.∴∽……………(1分)
∴,即,∴ …………………(2分)
(2)∵点是边的中点,∴…………………(2分)
∴ .…………………………………(3分)
21.(1)证明:∵平分,∴.……………………(1分)
∵DE∥BC ,∴ ……………………………(1分)
∴.∴ ……………………………(1分)
∵DE∥BC ,∴ ……………………………………(1分)
∴,∴ ………………………(1分)
(2)解:设中边上的高为.
∴,…………………………………(2分)
∵DE∥BC,∴. ………………………………………(1分)
∴,∴. …………………………………………(2分)
22.解: 由题意,得. ……………………………………(2分)
【方法一】过点作,垂足为.……………………………………(1分)
在中,,
∴, ……(2分)
在中,, …(1分)
∴ …………………………………………(2分)
∴≈.…(2分)
【方法二】过点作,交延长线于. ………………………(1分)
在中,,
设,∴. ………………………(2分)
∵ ……………(1分)
∴,∴ ,得 ……………………(2分)
∴ …………………(2分)
答:小岛离开深水港口的距离是千米.
23.证明: 延长到,使得.……………………………………(2分)
∴,……………………………………………………(2分)
∵,………………………………(2分)
∵,∴,又
∴∽ …………………………………………………(2分)
∴,即………………………………………(2分)
∴………………………………………………………(2分)
24.解:(1)由题意,得抛物线对称轴是直线,……………………………(1分)
∵点和点关于直线对称,点,∴………(1分)
∵,∴…………………………(1分)
∵点在轴正半轴上,∴ ………………………………(1分)
∴ ………………………………………………(2分)
(2)由题意,可得,, …………………(1分)
∵,∴,又
∴∽ ,∴ ………………………(1分)
∴和相似时,分下列两种情况:
当时,得,∴,
∴,∴.………………………(2分)
当时,得,∴,
∴,∴.………………(2分)
综合,当和相似时或.
25.解:(1)过点作∥,交于点.………………………………(1分)
∴,∵,
∴,∴
∵∥,∴四边形是平行四边形;
∴,,∴
在中,,∴,
∴ ………………………(1分)
∴ …………………………(1分)
∴.…………………………………(1分)
(2)过点作,垂足为.∴,…(1分)
∴,∴,
∴,∴,
∵点是边的中点,∴,
∴ ;…………………………………………………………(2分)
定义域是<< .…………………………………………………(1分)
(3)分别延长交于点 ,联结.
∵,∴,;
∴.
直线与直线交于点,当时,分两种情况:
当点在的延长线上时,
∵,∴;∵,
∴,∴;
∵,∴;∴,
∴;∴.…(3分)
当点在的延长线上时,
∵,,∴,
∴,∴,∴.…(3分)
综合、 ,当时,或.
期终学习能力诊断卷 2013、1
(时间100分钟 满分150分)
考生注意∶
1.本试卷含三个大题,共25题;答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;
2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.
一.选择题(本大题共6题,每题4分,满分24分)
【下列各题的四个选项中,有且只有一个选项是正确的】
1.在中,,,,那么等于…………( )
A.; B..; C.; D..
2.将抛物线沿轴向上平移1个单位后所得抛物线的解析式是 …………( )
A.; B.; C.; D..
3.坡比等于1∶的斜坡的坡角等于 ………………………………………………( )
A.; B.; C.; D..
4.关于二次函数的图像,下列说法正确的是…………………………( ).
A.开口向下; B.最低点是;
C.对称轴是直线; D.对称轴的右侧部分是上升的.
5.如图1,相交于点,下列条件中能判定∥的是 …………( )
A.; B.;
C.; D..
6.如图2,在中,,垂足为,那么下列结论中错误的
是………………………………………………………………………………………( )
A.; B.;
C.; D..
二.填空题(本大题共12题,每题4分,满分48分)
7.计算: ▲ .
8.计算: ▲ .
9.抛物线与轴的交点坐标是 ▲ .
10.如果两个相似三角形对应角平分线的比是,那么它们对应高的比是 ▲ .
11.如图3,已知∥∥,,,那么 ▲ .
12.点是线段上一点,,点分别是线段的中点,那么
等于 ▲ .
13.抛物线过和两点 ,那么该抛物线的对称轴是 ▲ .
14.在以O为坐标原点的直角坐标平面内有一点A(2,4),如果AO与x轴正半轴的夹角
为,那么= .
15.小明同学身高1.5米,经太阳光照射,在地面的影长为2米,他此时测得旗杆在同一地
面的影长为12米,那么旗杆高为 __ ▲ 米.
16.抛物线与x轴交于点(点在点的左侧),与轴交于点,且,,那么的值是 ▲ .
17.两个等腰直角三角形和的位置如图4所示,
点和点分别在一直线上,,
,,点分别是、
的重心,联结,那么 ▲ .
18.在中,,,,点是斜边AB的中点,把绕点旋转,使得点落在射线上,点落在点.那么的长是_____▲________.
三.(本大题共7题,第19—22题每题10分;第23、24题每题12分;第25题14分;
满分78分)
19.(本题满分10分)
抛物线经过点、两点.
(1)求抛物线顶点的坐标; (5分)
(2)抛物线与轴的另一交点为,求的面积. (5分)
20.(本题满分10分)
如图5,在中,点是边的中点,,.
(1)求的长; (5分)
(2)设,=,求向量(用向量、表示). (5分)
21.(本题满分10分)
如图6,在中,平分交于点,过点作∥交于
点.
(1)求证:; (5分)
(2)如果,,,求的长. (5分)
22.(本题满分10分)
如图7,小岛正好在深水港口的东南方向,一艘集装箱货船从港口出发,沿正东方向以每小时30千米的速度行驶,分钟后在处测得小岛在它的南偏东方向,求小岛离开深水港口的距离.(精确到千米)
参考数据:,,,,.
23.(本题满分12分)
“数学迷”小楠通过从“特殊到一般”的过程,对倍角三角形(一个内角是另一个内角的2倍的三角形)进行研究.得出结论:如图8,在中,的对边分别是,如果,那么.
下面给出小楠对其中一种特殊情形的一种证明方法.
已知:如图9,在中,,.
求证:.
证明:如图9,延长到,使得.
∴,
∵,
∴,∵,
∴,又
∴∽
∴,即
∴
根据上述材料提供的信息,请你完成下列情形的证明(用不同于材料中的方法也可以):
已知:如图8,在中,.
求证:.
24.(本题满分12分)
抛物线与轴正半轴交于点,与轴分别交于点和点,
且.
(1)求抛物线的解析式; (6分)
(2)点是轴上一点,当和相似时,求点的坐标. (6分)
25.(本题满分14分)
梯形中,∥,,,,,
点是边的中点,点是边上的动点.
(1)如图10,求梯形的周长; (4分)
(2)如图11,联结,设,(<<),求关于的关系式及定义域; (4分)
(3)如果直线与直线交于点,当时,求的长. (6分)
2012学年第一学期徐汇区初三年级数学学科
期终学习能力诊断卷参考答案和评分标准
一、选择题:(本大题共6题,每题4分,满分24分)
1.C; 2.B; 3.A; 4.D; 5.D; 6.B.
二.填空题:(本大题共12题,满分48分)
7.; 8.; 9.; 10.; 11.; 12.(或);
13.直线; 14.; 15.; 16.或; 17.(或); 18..
三、(本大题共7题,第19、20、21、22题每题10分,第23、24题每题12分,第25题14分,满分78分)
19. 解:(1)由题意,得………………………………………(1分)
解得………………………………………………………(1分)
∴………………………………………………(1分)
∴……………………………………………………………(2分)
(2)由题意,得,解得;
∴ …………………………………………………………(2分)
又、
∴ …………………………………………(3分)
20.解:(1)∵点是边的中点,,∴(1分)
∴,………………………………(1分)
∴,又.∴∽……………(1分)
∴,即,∴ …………………(2分)
(2)∵点是边的中点,∴…………………(2分)
∴ .…………………………………(3分)
21.(1)证明:∵平分,∴.……………………(1分)
∵DE∥BC ,∴ ……………………………(1分)
∴.∴ ……………………………(1分)
∵DE∥BC ,∴ ……………………………………(1分)
∴,∴ ………………………(1分)
(2)解:设中边上的高为.
∴,…………………………………(2分)
∵DE∥BC,∴. ………………………………………(1分)
∴,∴. …………………………………………(2分)
22.解: 由题意,得. ……………………………………(2分)
【方法一】过点作,垂足为.……………………………………(1分)
在中,,
∴, ……(2分)
在中,, …(1分)
∴ …………………………………………(2分)
∴≈.…(2分)
【方法二】过点作,交延长线于. ………………………(1分)
在中,,
设,∴. ………………………(2分)
∵ ……………(1分)
∴,∴ ,得 ……………………(2分)
∴ …………………(2分)
答:小岛离开深水港口的距离是千米.
23.证明: 延长到,使得.……………………………………(2分)
∴,……………………………………………………(2分)
∵,………………………………(2分)
∵,∴,又
∴∽ …………………………………………………(2分)
∴,即………………………………………(2分)
∴………………………………………………………(2分)
24.解:(1)由题意,得抛物线对称轴是直线,……………………………(1分)
∵点和点关于直线对称,点,∴………(1分)
∵,∴…………………………(1分)
∵点在轴正半轴上,∴ ………………………………(1分)
∴ ………………………………………………(2分)
(2)由题意,可得,, …………………(1分)
∵,∴,又
∴∽ ,∴ ………………………(1分)
∴和相似时,分下列两种情况:
当时,得,∴,
∴,∴.………………………(2分)
当时,得,∴,
∴,∴.………………(2分)
综合,当和相似时或.
25.解:(1)过点作∥,交于点.………………………………(1分)
∴,∵,
∴,∴
∵∥,∴四边形是平行四边形;
∴,,∴
在中,,∴,
∴ ………………………(1分)
∴ …………………………(1分)
∴.…………………………………(1分)
(2)过点作,垂足为.∴,…(1分)
∴,∴,
∴,∴,
∵点是边的中点,∴,
∴ ;…………………………………………………………(2分)
定义域是<< .…………………………………………………(1分)
(3)分别延长交于点 ,联结.
∵,∴,;
∴.
直线与直线交于点,当时,分两种情况:
当点在的延长线上时,
∵,∴;∵,
∴,∴;
∵,∴;∴,
∴;∴.…(3分)
当点在的延长线上时,
∵,,∴,
∴,∴,∴.…(3分)
综合、 ,当时,或.
同课章节目录
