上海市嘉定区2013年中考一模(即期末)数学试题
文档属性
| 名称 | 上海市嘉定区2013年中考一模(即期末)数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 344.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-25 18:19:58 | ||
图片预览




文档简介
2012学年嘉定区九年级第一次质量调研
数学试卷
(满分150分,考试时间100分钟)
考生注意:
1.本试卷含三个大题,共25题;
2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;
3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.
一、选择题:(本大题共6题,每题4分,满分24分)
【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.】
一、选择题:(本大题共6题,每题4分,满分24分)
1. 对于线段、,如果,那么下列四个选项一定正确的是(▲)
(A); (B); (C); (D).
2. 如图1,在直角坐标平面内有一点,那么射线与轴正半轴的
夹角的余弦值是(▲)
(A); (B); (C); (D).
3. 已知抛物线如图2所示,那么、的取值范围是(▲)
(A),; (B),;
(C),; (D),.
4.下列四个命题中,真命题的个数为(▲)
①面积相等的两个直角三角形相似;
②周长相等的两个直角三角形相似;
③有一个锐角相等的两个直角三角形相似;
④斜边和直角边对应成比例的两个直角三角形相似.
(A); (B); (C); (D).
5.正多边形的一个内角的度数不可能是(▲)
(A); (B); (C); (D).
6. 已知⊙的半径长为,若⊙(与不重合)上的点满足,则下列位置关系中,⊙与⊙不可能存在的位置关系是(▲)
(A)相交; (B)内切; (C)外切; (D)外离.
二、填空题(本大题共12题,每题4分,满分48分)
7. 如图3,在△ABC中,∥,与边相交于点,与边
相交于点,如果,,,那么的长为 ▲ .
8. 已知,,且与反向,如果用向量表示向量,那么= ▲ .
9. 如图4,飞机在目标的正上方米处.如果飞行员测得目标的俯角
为,那么地面目标、之间的距离为 ▲ 米(结果保留根号).
10.如果二次函数的图像经过原点,那么的值为 ▲ .
11.二次函数的图像在轴左侧的部分是 ▲ 的.(从“上升”或“下降”中选择).
12.二次函数图像的对称轴是直线 ▲ .
13.把抛物线先向右平移3个单位,再向下平移2个单位,所得抛物线的顶点坐标是 ▲ .
14.已知⊙的半径长为,点满足,那么过点的直线与⊙
不可能存在的位置关系是 ▲ (从“相交”、“相切”、“相离”中选择).
15.正六边形的边心距与半径长的比值为 ▲ .
16.对于平面图形,如果存在一个圆,使图形上的任意一点到圆心的距离都不大于这个圆的半径,则称图形被这个圆“覆盖”.例如图5中的三角形被一个圆“覆盖”.如果边长为的正六边形被一个半径长为的圆“覆盖”,那么的取值范围为 ▲ .
17.如图6,已知⊙与⊙相交于点、,,,⊙的半径长为,那么⊙的半径长为 ▲ .
18.如图7,弧所在的⊙的半径长为,正三角形的顶点、分别在半径、上,点在弧上,.如果,那么这个正三角形的边长为 ▲ .
三、简答题(本大题共7题,满分78分)
19.(本题满分10分)
计算:.
20.(本题满分10分)
如图8,已知△ABC中,,,矩形
的边在△ABC的边上,顶点、分别在
边、上,设的长为,矩形的面积为.
求关于的函数关系式,并写出这个函数的定义域.
21.(本题满分10分,第(1)小题5分,第(2)小题5分)
如图9,已知点、分别在△ABC的边和上,∥,,四边形的面积等于.
(1)求△ABC的面积;
(2)如果向量,向量,请用、表示向量.
22.(本题满分10分,第(1)小题6分,第(2)小题4分)
如图10,一条细绳系着一个小球在平面内摆动.已知细绳从悬挂点到球心的长度为厘米,小球在左、右两个最高位置时(不考虑阻力等其他因素),细绳相应所成的角为.
(1)求小球在最高位置和最低位置时的高度差;
(2)联结,求的余切值.
23.(本题满分12分,第(1)小题6分,第(2)小题6分)
已知:点是的边的一个动点(如图11),过点作,垂足为,点在边上(点与点不重合),且满足,联结、.
(1)当平分时,求证:;
(2)若,.当时,求的长.
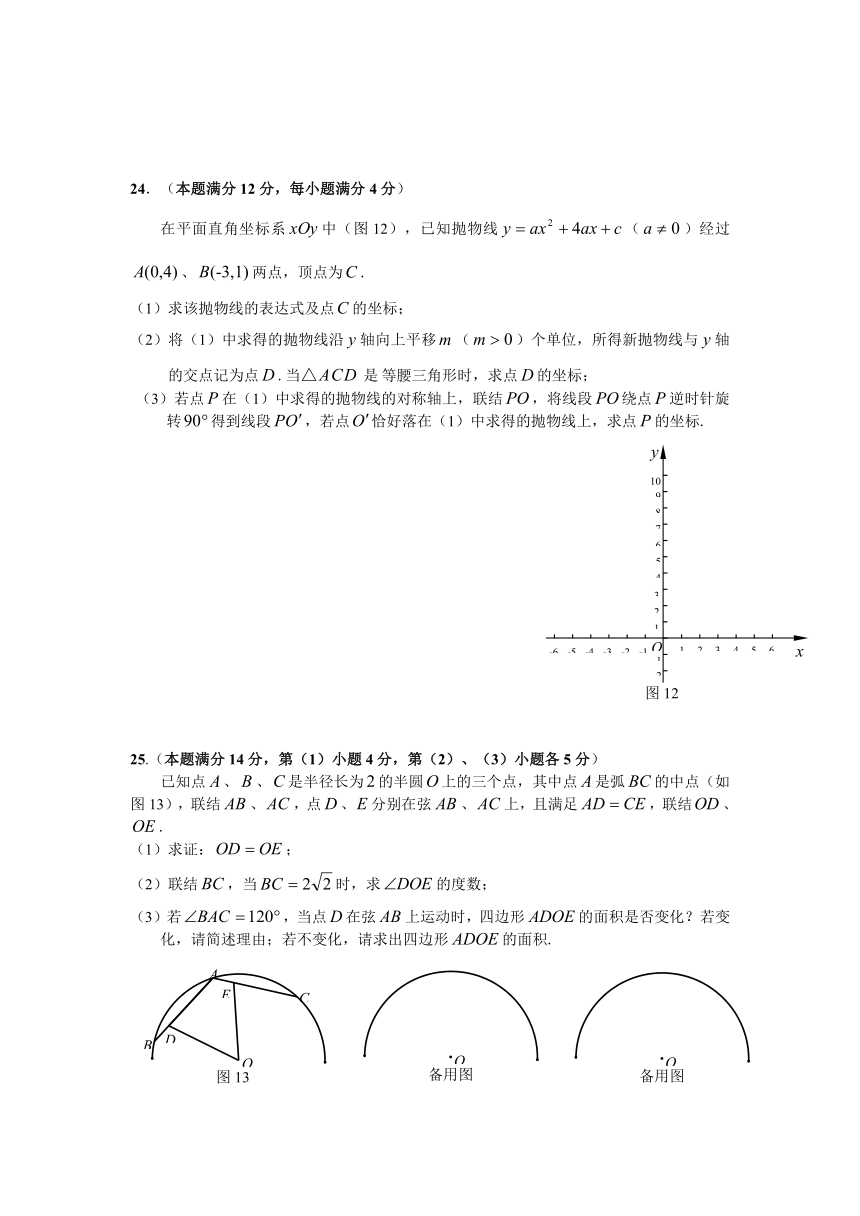
24.(本题满分12分,每小题满分4分)
在平面直角坐标系中(图12),已知抛物线()经过、两点,顶点为.
(1)求该抛物线的表达式及点的坐标;
(2)将(1)中求得的抛物线沿轴向上平移()个单位,所得新抛物线与轴的交点记为点.当△ACD是等腰三角形时,求点的坐标;
(3)若点在(1)中求得的抛物线的对称轴上,联结,将线段绕点逆时针旋转得到线段,若点恰好落在(1)中求得的抛物线上,求点的坐标.
25.(本题满分14分,第(1)小题4分,第(2)、(3)小题各5分)
已知点、、是半径长为的半圆上的三个点,其中点是弧的中点(如图13),联结、,点、分别在弦、上,且满足,联结、.
(1)求证:;
(2)联结,当时,求的度数;
(3)若,当点在弦上运动时,四边形的面积是否变化?若变化,请简述理由;若不变化,请求出四边形的面积.
2012学年嘉定区九年级第一次质量调研
数学试卷答案要点与评分标准
说 明:
1.解答只列出试题的一种或几种解法.如果学生的解法与所列解法不同,可参照解答中评分标准相应评分;
2.第一、二大题若无特殊说明,每题评分只有满分或零分;答案若为分数,需要化成最简分数.
3.第三大题中各题右端所注分数,表示学生正确解答到这一步应得分数;
4.评阅试卷,要坚持每题评阅到底,不能因学生解答中出现错误而中断对本题的评阅.如果学生的解答在某一步出现错误,影响后继部分而未改变本题解答的实质,视影响的程度决定后继部分的给分,但原则上不超过后继部分应得分数的一半;
5.评分时,给分或扣分均以1分为基本单位.
一、选择题:(本大题共6题,每题4分,满分24分)
1.C; 2.C; 3.B; 4.C; 5.A; 6.D.
二、填空题(本大题共12题,每题4分,满分48分)
7.(或者); 8.; 9.; 10.;
11.下降; 12.; 13.(4,2); 14.相离;
15.; 16.; 17.; 18..
三、简答题(本大题共7题,满分78分)
19.解:=…………(6分)
.……………………………(2+1+1)分
20.解:过点作,交于,交于(如图8).…………(1分)
∵四边形,在边上,
∴∥.…………………………………………………………………(1分)
得 △ADG∽△ABC.………………………………………………………(1分)
∵∥,,∴.
∴.……………………………………………………………(1分)
在△ABC中,∵,,,∴.
.…………………………………(1分)
∵,,∴∥.
又∥, ∴.∴.…(1分)
由,,得
.………………………………………………………………(1分)
解得 .……………………………… ……………………(1分)
∴.………………………………………(1分)
定义域为.…………………………………………………………(1分)
21.解:(1)∵∥,∴△ADE∽△ABC.∴.………(1+1分)
∵,∴. ∴.…………………………(1分)
又∵,∴.解得 .………………(1分)
∴.………………………………………………………(1分)
(2)∵向量,向量,∴向量.…………………(1分)
∵∥,∴.………………………………………………(1分)
∵,∴.………………………… … ……………(1分)
∴ 向量.………………… ……… ……………(2分)
22.解:(1)过点作,垂足为点. ……………(1分)
小球在最高位置和最低位置时的高度差就是的长.
根据题意,可知.………………(1分)
在中,∵,
∴. …… (2分)
∴.…………………………(2分)
(2)联结.…………………………………………………(1分)
在中,.…………(1分)
∴.……………(2分)
23.解:(1)∵,,
∴,.………………………………(1分)
∵平分,∴.
∵,∴. …… …………(1分)
又∵,∴△DCF∽△FCB. ………………(1分)
∴.………………………………………………(2分)
∵,∴. …………………………(1分)
(2)在中,由,,
易得,,,.………………………(1分)
过点作,垂足为(如图11-2).
在Rt△BCH中,.………………………(1分)
.
设(备注:也可以设),
在Rt△BDE中,,.
由,可得. …………………(1分)
由,易得,
又,∴.
方法1:∴.………………………………………(1分)
∵,,
∴. …………………………………(1分)
解得.即.………………………(1分)
方法2:∴△HCF∽△EFD. …………………(1分)
∴.
将,,,代入上式,得
. ……………………………………………………………………(1分)
解得 .即.………………………………………………………(1分)
24.解:(1)由抛物线经过,,
得……………………………………………………………(1分)
解这个方程组,得 ……………………………………………………(1分)
因此,所求的抛物线的表达式为.…………………………………(1分)
由,易得顶点的坐标为(,).…………(1分)
(2)因为点是将抛物线沿轴向上
平移()个单位所得新抛物线与轴的交点.
所以,点必定在点的上方(如图12-1),
得 .………………………………(1分)
∵△ACD是等腰三角形,∴.………………(1分)
在Rt△AOC中,,,由勾股定理可得
.
∴,.……(1分)
∴点的坐标为(,).………………………(1分)
(3)因为点在抛物线的对称轴上,故
可设点的坐标为(,).
由题意知:,.
过点作,垂足为.
∵,.
∴.
∵,,
,∴△≌△.
∴,.
当点在第二象限时(如图12-2),
,,.
故而可得点的坐标为(,).……(1分)
备注:若点在第一象限,其坐标也是(,),下同.
∵点(,)恰好在上,∴.
整理,得 .解得 ,(舍去).
故可得点(,).……………………………(1分)
当点在第三象限时(如图12-3),
,,.
由此可得点的坐标为(,)……(1分)
∵(,)在抛物线上,
∴ .
整理,得 ,解得(舍去),.
故而可知(,). ………(1分)
25.解:(1)方法1:联结、、(如图13-1),易得.
在⊙中,∵,∴.…………………… ……(1分)
∵,,,∴△AOB≌△AOC.
∴. ………………………………………………(1分)
又 ∵,∴.
∴.
∵,,,
∴△AOD≌△COE.…………………………………………(1分)
∴. ……………………………………………………(1分)
方法2:在⊙中,∵,∴. …………………(1分)
过点分别作,,垂足分别为、(如图13-2),
∵,,∴,.
由 易得 ,.……………………(1分)
∵,,∴,即 .
∵,,,
∴△ODM≌△OEN. ……………………………………………………(1分)
∴. ……………………………………………………………(1分)
(2)如图13-3,在△BOC中,由,,得
,.
∴. ∴. ………(1+1分)
∵,是圆心,
∴. ………………………………(1分)
∵△AOD≌△COE,∴.………………………………………(1分)
∴.……………(1分)
若使用锐角三角比或其他方法,请参照评分.
(3)当点在弦上运动时,四边形的面积不变.理由如下:…………(1分)
∵,
∴,……………(1分)
又∵,∴△AOC是等边三角形.
∴.…………………………………………(1分)
由(1)中的△AOD≌△COE,可知.
∴.……(1分)
过点作,垂足为,易得,
∴. …………………(1分)
数学试卷
(满分150分,考试时间100分钟)
考生注意:
1.本试卷含三个大题,共25题;
2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;
3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.
一、选择题:(本大题共6题,每题4分,满分24分)
【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.】
一、选择题:(本大题共6题,每题4分,满分24分)
1. 对于线段、,如果,那么下列四个选项一定正确的是(▲)
(A); (B); (C); (D).
2. 如图1,在直角坐标平面内有一点,那么射线与轴正半轴的
夹角的余弦值是(▲)
(A); (B); (C); (D).
3. 已知抛物线如图2所示,那么、的取值范围是(▲)
(A),; (B),;
(C),; (D),.
4.下列四个命题中,真命题的个数为(▲)
①面积相等的两个直角三角形相似;
②周长相等的两个直角三角形相似;
③有一个锐角相等的两个直角三角形相似;
④斜边和直角边对应成比例的两个直角三角形相似.
(A); (B); (C); (D).
5.正多边形的一个内角的度数不可能是(▲)
(A); (B); (C); (D).
6. 已知⊙的半径长为,若⊙(与不重合)上的点满足,则下列位置关系中,⊙与⊙不可能存在的位置关系是(▲)
(A)相交; (B)内切; (C)外切; (D)外离.
二、填空题(本大题共12题,每题4分,满分48分)
7. 如图3,在△ABC中,∥,与边相交于点,与边
相交于点,如果,,,那么的长为 ▲ .
8. 已知,,且与反向,如果用向量表示向量,那么= ▲ .
9. 如图4,飞机在目标的正上方米处.如果飞行员测得目标的俯角
为,那么地面目标、之间的距离为 ▲ 米(结果保留根号).
10.如果二次函数的图像经过原点,那么的值为 ▲ .
11.二次函数的图像在轴左侧的部分是 ▲ 的.(从“上升”或“下降”中选择).
12.二次函数图像的对称轴是直线 ▲ .
13.把抛物线先向右平移3个单位,再向下平移2个单位,所得抛物线的顶点坐标是 ▲ .
14.已知⊙的半径长为,点满足,那么过点的直线与⊙
不可能存在的位置关系是 ▲ (从“相交”、“相切”、“相离”中选择).
15.正六边形的边心距与半径长的比值为 ▲ .
16.对于平面图形,如果存在一个圆,使图形上的任意一点到圆心的距离都不大于这个圆的半径,则称图形被这个圆“覆盖”.例如图5中的三角形被一个圆“覆盖”.如果边长为的正六边形被一个半径长为的圆“覆盖”,那么的取值范围为 ▲ .
17.如图6,已知⊙与⊙相交于点、,,,⊙的半径长为,那么⊙的半径长为 ▲ .
18.如图7,弧所在的⊙的半径长为,正三角形的顶点、分别在半径、上,点在弧上,.如果,那么这个正三角形的边长为 ▲ .
三、简答题(本大题共7题,满分78分)
19.(本题满分10分)
计算:.
20.(本题满分10分)
如图8,已知△ABC中,,,矩形
的边在△ABC的边上,顶点、分别在
边、上,设的长为,矩形的面积为.
求关于的函数关系式,并写出这个函数的定义域.
21.(本题满分10分,第(1)小题5分,第(2)小题5分)
如图9,已知点、分别在△ABC的边和上,∥,,四边形的面积等于.
(1)求△ABC的面积;
(2)如果向量,向量,请用、表示向量.
22.(本题满分10分,第(1)小题6分,第(2)小题4分)
如图10,一条细绳系着一个小球在平面内摆动.已知细绳从悬挂点到球心的长度为厘米,小球在左、右两个最高位置时(不考虑阻力等其他因素),细绳相应所成的角为.
(1)求小球在最高位置和最低位置时的高度差;
(2)联结,求的余切值.
23.(本题满分12分,第(1)小题6分,第(2)小题6分)
已知:点是的边的一个动点(如图11),过点作,垂足为,点在边上(点与点不重合),且满足,联结、.
(1)当平分时,求证:;
(2)若,.当时,求的长.
24.(本题满分12分,每小题满分4分)
在平面直角坐标系中(图12),已知抛物线()经过、两点,顶点为.
(1)求该抛物线的表达式及点的坐标;
(2)将(1)中求得的抛物线沿轴向上平移()个单位,所得新抛物线与轴的交点记为点.当△ACD是等腰三角形时,求点的坐标;
(3)若点在(1)中求得的抛物线的对称轴上,联结,将线段绕点逆时针旋转得到线段,若点恰好落在(1)中求得的抛物线上,求点的坐标.
25.(本题满分14分,第(1)小题4分,第(2)、(3)小题各5分)
已知点、、是半径长为的半圆上的三个点,其中点是弧的中点(如图13),联结、,点、分别在弦、上,且满足,联结、.
(1)求证:;
(2)联结,当时,求的度数;
(3)若,当点在弦上运动时,四边形的面积是否变化?若变化,请简述理由;若不变化,请求出四边形的面积.
2012学年嘉定区九年级第一次质量调研
数学试卷答案要点与评分标准
说 明:
1.解答只列出试题的一种或几种解法.如果学生的解法与所列解法不同,可参照解答中评分标准相应评分;
2.第一、二大题若无特殊说明,每题评分只有满分或零分;答案若为分数,需要化成最简分数.
3.第三大题中各题右端所注分数,表示学生正确解答到这一步应得分数;
4.评阅试卷,要坚持每题评阅到底,不能因学生解答中出现错误而中断对本题的评阅.如果学生的解答在某一步出现错误,影响后继部分而未改变本题解答的实质,视影响的程度决定后继部分的给分,但原则上不超过后继部分应得分数的一半;
5.评分时,给分或扣分均以1分为基本单位.
一、选择题:(本大题共6题,每题4分,满分24分)
1.C; 2.C; 3.B; 4.C; 5.A; 6.D.
二、填空题(本大题共12题,每题4分,满分48分)
7.(或者); 8.; 9.; 10.;
11.下降; 12.; 13.(4,2); 14.相离;
15.; 16.; 17.; 18..
三、简答题(本大题共7题,满分78分)
19.解:=…………(6分)
.……………………………(2+1+1)分
20.解:过点作,交于,交于(如图8).…………(1分)
∵四边形,在边上,
∴∥.…………………………………………………………………(1分)
得 △ADG∽△ABC.………………………………………………………(1分)
∵∥,,∴.
∴.……………………………………………………………(1分)
在△ABC中,∵,,,∴.
.…………………………………(1分)
∵,,∴∥.
又∥, ∴.∴.…(1分)
由,,得
.………………………………………………………………(1分)
解得 .……………………………… ……………………(1分)
∴.………………………………………(1分)
定义域为.…………………………………………………………(1分)
21.解:(1)∵∥,∴△ADE∽△ABC.∴.………(1+1分)
∵,∴. ∴.…………………………(1分)
又∵,∴.解得 .………………(1分)
∴.………………………………………………………(1分)
(2)∵向量,向量,∴向量.…………………(1分)
∵∥,∴.………………………………………………(1分)
∵,∴.………………………… … ……………(1分)
∴ 向量.………………… ……… ……………(2分)
22.解:(1)过点作,垂足为点. ……………(1分)
小球在最高位置和最低位置时的高度差就是的长.
根据题意,可知.………………(1分)
在中,∵,
∴. …… (2分)
∴.…………………………(2分)
(2)联结.…………………………………………………(1分)
在中,.…………(1分)
∴.……………(2分)
23.解:(1)∵,,
∴,.………………………………(1分)
∵平分,∴.
∵,∴. …… …………(1分)
又∵,∴△DCF∽△FCB. ………………(1分)
∴.………………………………………………(2分)
∵,∴. …………………………(1分)
(2)在中,由,,
易得,,,.………………………(1分)
过点作,垂足为(如图11-2).
在Rt△BCH中,.………………………(1分)
.
设(备注:也可以设),
在Rt△BDE中,,.
由,可得. …………………(1分)
由,易得,
又,∴.
方法1:∴.………………………………………(1分)
∵,,
∴. …………………………………(1分)
解得.即.………………………(1分)
方法2:∴△HCF∽△EFD. …………………(1分)
∴.
将,,,代入上式,得
. ……………………………………………………………………(1分)
解得 .即.………………………………………………………(1分)
24.解:(1)由抛物线经过,,
得……………………………………………………………(1分)
解这个方程组,得 ……………………………………………………(1分)
因此,所求的抛物线的表达式为.…………………………………(1分)
由,易得顶点的坐标为(,).…………(1分)
(2)因为点是将抛物线沿轴向上
平移()个单位所得新抛物线与轴的交点.
所以,点必定在点的上方(如图12-1),
得 .………………………………(1分)
∵△ACD是等腰三角形,∴.………………(1分)
在Rt△AOC中,,,由勾股定理可得
.
∴,.……(1分)
∴点的坐标为(,).………………………(1分)
(3)因为点在抛物线的对称轴上,故
可设点的坐标为(,).
由题意知:,.
过点作,垂足为.
∵,.
∴.
∵,,
,∴△≌△.
∴,.
当点在第二象限时(如图12-2),
,,.
故而可得点的坐标为(,).……(1分)
备注:若点在第一象限,其坐标也是(,),下同.
∵点(,)恰好在上,∴.
整理,得 .解得 ,(舍去).
故可得点(,).……………………………(1分)
当点在第三象限时(如图12-3),
,,.
由此可得点的坐标为(,)……(1分)
∵(,)在抛物线上,
∴ .
整理,得 ,解得(舍去),.
故而可知(,). ………(1分)
25.解:(1)方法1:联结、、(如图13-1),易得.
在⊙中,∵,∴.…………………… ……(1分)
∵,,,∴△AOB≌△AOC.
∴. ………………………………………………(1分)
又 ∵,∴.
∴.
∵,,,
∴△AOD≌△COE.…………………………………………(1分)
∴. ……………………………………………………(1分)
方法2:在⊙中,∵,∴. …………………(1分)
过点分别作,,垂足分别为、(如图13-2),
∵,,∴,.
由 易得 ,.……………………(1分)
∵,,∴,即 .
∵,,,
∴△ODM≌△OEN. ……………………………………………………(1分)
∴. ……………………………………………………………(1分)
(2)如图13-3,在△BOC中,由,,得
,.
∴. ∴. ………(1+1分)
∵,是圆心,
∴. ………………………………(1分)
∵△AOD≌△COE,∴.………………………………………(1分)
∴.……………(1分)
若使用锐角三角比或其他方法,请参照评分.
(3)当点在弦上运动时,四边形的面积不变.理由如下:…………(1分)
∵,
∴,……………(1分)
又∵,∴△AOC是等边三角形.
∴.…………………………………………(1分)
由(1)中的△AOD≌△COE,可知.
∴.……(1分)
过点作,垂足为,易得,
∴. …………………(1分)
同课章节目录
