广西壮族自治区2022年普通高中学业水平考试数学拔高卷(4月)(Word版含答案)
文档属性
| 名称 | 广西壮族自治区2022年普通高中学业水平考试数学拔高卷(4月)(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 313.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-04 11:20:57 | ||
图片预览




文档简介
2022广西普通高中学业水平考试 拔高卷
数 学
(全卷满分 100 分,考试时间 120 分钟)
注意事项:
1.答题前,考生务必将自己的姓名、座位号、考籍号填写在答题卡上.
2.考生作答时,请在答题卡上作答(答题注意事项见答题卡),在本试题上作答无效.
一、选择题:本大题共 20 小题,每小题 3 分,共 60 分.在每小题给出的四个选项中,只 有一项是符合题目要求的.
1.表示集合中整数元素的个数,设集合,,则( )
A. B. C. D.
2.已知复数满足,则的共轭复数是( )
A. B. C. D.
3.已知函数是定义在上的偶函数,且在上单调递增,则( )
A. B.
C. D.
4.宋代诗词大师欧阳修的《卖油翁》中有一段关于卖油翁的精湛技艺的细节描写:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿.”如果铜钱是直径为的圆,钱中间的正方形孔的边长为,则卖油翁向葫芦内注油,油正好进入孔中的概率是( )
A. B. C. D.
5.命题:,,命题:,,则是的( )
A.充分非必要条件 B.必要非充分条件
C.必要充分条件 D.既不充分也不必要条件
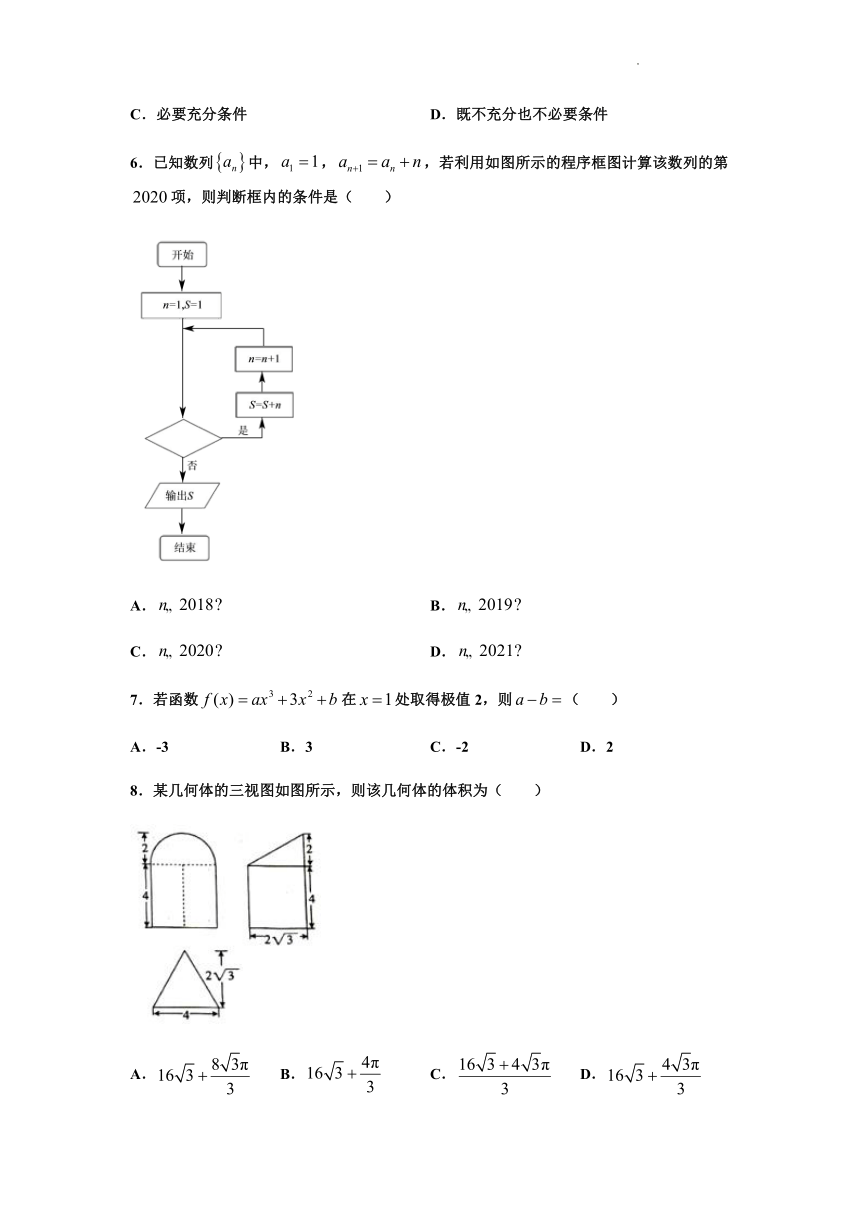
6.已知数列中,,,若利用如图所示的程序框图计算该数列的第项,则判断框内的条件是( )
A. B.
C. D.
7.若函数在处取得极值2,则( )
A.-3 B.3 C.-2 D.2
8.某几何体的三视图如图所示,则该几何体的体积为( )
A. B. C. D.
9.设,则( )
A. B. C. D.
10.给出下列三个命题:
①“”的否定;
②在中,“”是“”的充要条件;
③将函数的图象向左平移个单位长度,得到函数的图象.
其中假命题的个数是( )
A.0 B.1 C.2 D.3
11.将函数图象向右平移个单位长度,所得图象对应的函数
A. 在区间上单调递减 B. 在区间上单调递增
C. 在区间上单调递减 D. 在区间上单调递增
12.若点A的坐标为(3,1),F为抛物线y2=2x的焦点,点P是抛物线上的一动点,则|PA|+|PF|取最小值时点P的坐标为
A. (0,0) B. (1,1) C. (2,2) D. (,1)
13.某几何体三视图如图所示,则该几何体表面积为
A. B.
C. D.
14.已知函数f(x)是(﹣∞,+∞)上的减函数,
那么a的取值范围是
A. (0,1) B. (0,) C. [,) D. (,)
15.若则
A. B. 2 C. D. -2
16.设x,y满足约束条件,目标函数z=ax+by(a>0,b>0)的最大值为2,则的最小值为
A. 5 B. C. D. 9
17.已知非零向量,满足 ,且 ,则与的夹角为( )
A. B. C. D.
18.已知,则( )
A. B. C. D.
19.若函数在上的最大值为4,则的取值范围为( )
A. B. C. D.
20.17世纪德国著名的天文学家开普勒曾经这样说过:“几何学里有两件宝,一个是勾股定理,另一个是黄金分割.如果把勾股定理比作黄金矿的话,那么可以把黄金分割比作钻石矿.”黄金三角形有两种,其中底与腰之比为黄金分割比的黄金三角形被认为是最美的三角形,它是一个顶角为的等腰三角形(另一种是顶角为的等腰三角形).例如,五角星由五个黄金三角形与一个正五边形组成,如图所示,在其中一个黄金中,.根据这些信息,可得( )
A. B. C. D.
二.填空题:本大题共 4 小题,每小题 3 分,共 12 分.
21.函数的最大值是___.
22.函数的值域为________.
23.为满足人民对美好生活的向往,环保部门要求相关企业加强污水治理,排放未达标的企业要限期整改,设企业的污水排放量W与时间t的关系为,用的大小评价在这段时间内企业污水治理能力的强弱,已知整改期内,甲、乙两企业的污水排放量与时间的关系如下图所示.
给出下列四个结论:
①在这段时间内,甲企业的污水治理能力比乙企业强;
②在时刻,甲企业的污水治理能力比乙企业强;
③在时刻,甲、乙两企业的污水排放都已达标;
④甲企业在这三段时间中,在的污水治理能力最强.
其中所有正确结论的序号是____________________.
24.已知函数,对一切,恒成立,则的取值范围是________.
三.解答题:本大题共 4 小题,共 28 分.解答应写出文字说明、证明过程或演算步骤.
25.设函数f(x)=ax-,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
(Ⅰ)求f(x)的解析式;
(Ⅱ)证明:曲线y=f(x)上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,并求此定值.
26.如图,在正四棱柱ABCD-A1B1C1D1中,E为AD中点, F为B1C1中点.
(1)求证:A1F∥平面ECC1;
(2)在CD上是否存在一点G,使BG⊥平面ECC1 若存
在,请确定点G的位置,并证明你的结论;若不存在,请说明理由.
27.某校某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图(已知本次测试成绩满分100分,且均为不低于50分的整数),请根据图表中的信息解答下列问题.
(1)求全班的学生人数及频率分布直方图中分数在[70,80)之间的矩形的高;
(2)为了帮助学生提高数学成绩,决定在班里成立“二帮一”小组,即从成绩[90,100]中选两位同学,共同帮助[50,60)中的某一位同学,已知甲同学的成绩为53分,乙同学的成绩为96分,求甲、乙恰好被安排在同一小组的概率.
28.已知函数f(x)=ax2-xln x.
(1)若f(x)在(0,+∞)上单调递增,求a的取值范围;
(2)若a=e(e为自然对数的底数),证明:当x>0时,f(x)样卷参考答案
一、选择题(共 20 小题,每小题 3 分,共 60 分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C D A B A D D C
题号 11 12 13 14 15 16 17 18 19 20
答案 B D D C B C C C C C
填空题(共 4 小题,每小题 3 分,共 12 分)
21.;
22.;
23.①②③;
24..
三、解答题(共 4 小题,共 28 分)
25.(Ⅰ)方程7x-4y-12=0可化为y=x-3.
当x=2时,y=.
又f '(x)=a+,
于是, 解得
故.
(Ⅱ)设P(x0,y0)为曲线上任一点,由y'=1+知曲线在点P(x0,y0)处的切线方程为,
即.
令x=0得y=-,从而得切线与直线x=0的交点坐标为( 0,).
令y=x得y=x=2x0,从而得切线与直线y=x的交点坐标为(2x0,2x0).
所以点P(x0,y0)处的切线与直线x=0,y=x所围成的三角形面积为
故曲线y=f(x)上任一点处的切线与直线x=0,y=x所围成的三角形的面积为定值,此定值为6.
26.
(1)如图,在正四棱柱ABCD-A1B1C1D1中,取BC的中点M,连接AM,FM.
∴B1F∥BM且B1F=BM,
∴四边形B1FMB是平行四边形,
∴FM∥B1B且FM=B1B.
∴FM∥A1A且FM=A1A,
∴四边形AA1FM是平行四边形,
∴FA1∥AM.
∵E为AD中点,
∴AE∥MC且AE=MC,
∴四边形AMCE是平行四边形,
∴CE∥AM,∴CE∥A1F.
∵A1F 平面ECC1,EC 平面ECC1,∴A1F∥平面ECC1.
(2)在CD上存在一点G,使BG⊥平面ECC1,此时G为CD的中点.
取CD的中点G,连接BG,如图D 8-4-9.
∵DE=GC,CD=BC,∠ADC=∠BCD,
∴△CDE≌△BCG, ∴∠ECD=∠GBC.
∵∠CGB+∠GBC=90°,∴∠CGB+∠DCE=90°,∴BG⊥EC.
∵CC1⊥平面ABCD,BG 平面ABCD,
∴CC1⊥BG,又EC∩CC1=C,∴BG⊥平面ECC1.
故在CD上存在中点G,使BG⊥平面ECC1.
27.
【解】(1)由茎叶图知分数在[50,60)上的频数为4,频率为0.008×10=0.08,
故全班的学生人数为50人,
∵分数在[70,80)间的频数为:50﹣(4+14+8+4)=20,
∴频率是,∴矩形的高是0.04.
(2)成绩在[50,60)分数段内的人数有4人,记为甲、A、B、C,成绩在[90,100)分数段内的人数有4人,记为乙、a,b,c,则“二帮一”小组有以下24种分组办法:
甲乙a,甲乙b,甲乙c,甲ab,甲ac,甲bc,A乙a,A乙b,
A乙c,Aab,Aac,Abc,B乙a,B乙b,B乙c,Bab,
Bac,Bbc,C乙a,C乙b,C乙c,Cab,Cac,Cbc,
其中,甲、乙两同学被分在同一小组有3种办法:甲乙a,甲乙b,甲乙c,
∴甲乙两同学恰好被安排在同一小组的概率为P.
28.
(1)f '(x)=2ax-ln x-1.
因为f(x)在(0,+∞)上单调递增,所以当x>0时,f '(x)≥0恒成立,
即2ax-ln x-1≥0恒成立,即2a≥恒成立.
设g(x)=,则2a≥g(x)max.
g'(x)=-,由g'(x)>0,得ln x<0,即00,即x>1.
所以g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
则g(x)max=g(1)=1.
所以2a≥1,即a≥,故a的取值范围是[,+∞).
(2)当a=e时,要证f(x)因为x>0,所以只需证ex-ln xex-ex.
设h(x)=ln x+,则h'(x)=(x>0).
由h'(x)<0,得00,得x>.则h(x)在(0,)上单调递减,在(,+∞)上单调递增.所以h(x)min=h()=0,从而h(x)≥0,即ln x+≥0.
设φ(x)=ex-ex(x>0),则φ'(x)=e-ex(x>0).
由φ'(x)>0,得01.则φ(x)在(0,1)上单调递增,在(1,+∞)上单调递减.所以φ(x)max=φ(1)=0,从而φ(x)≤0,即ex-ex≤0.
因为h(x)和φ(x)不同时为0,所以ln x+>ex-ex,故原不等式成立.
数 学
(全卷满分 100 分,考试时间 120 分钟)
注意事项:
1.答题前,考生务必将自己的姓名、座位号、考籍号填写在答题卡上.
2.考生作答时,请在答题卡上作答(答题注意事项见答题卡),在本试题上作答无效.
一、选择题:本大题共 20 小题,每小题 3 分,共 60 分.在每小题给出的四个选项中,只 有一项是符合题目要求的.
1.表示集合中整数元素的个数,设集合,,则( )
A. B. C. D.
2.已知复数满足,则的共轭复数是( )
A. B. C. D.
3.已知函数是定义在上的偶函数,且在上单调递增,则( )
A. B.
C. D.
4.宋代诗词大师欧阳修的《卖油翁》中有一段关于卖油翁的精湛技艺的细节描写:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿.”如果铜钱是直径为的圆,钱中间的正方形孔的边长为,则卖油翁向葫芦内注油,油正好进入孔中的概率是( )
A. B. C. D.
5.命题:,,命题:,,则是的( )
A.充分非必要条件 B.必要非充分条件
C.必要充分条件 D.既不充分也不必要条件
6.已知数列中,,,若利用如图所示的程序框图计算该数列的第项,则判断框内的条件是( )
A. B.
C. D.
7.若函数在处取得极值2,则( )
A.-3 B.3 C.-2 D.2
8.某几何体的三视图如图所示,则该几何体的体积为( )
A. B. C. D.
9.设,则( )
A. B. C. D.
10.给出下列三个命题:
①“”的否定;
②在中,“”是“”的充要条件;
③将函数的图象向左平移个单位长度,得到函数的图象.
其中假命题的个数是( )
A.0 B.1 C.2 D.3
11.将函数图象向右平移个单位长度,所得图象对应的函数
A. 在区间上单调递减 B. 在区间上单调递增
C. 在区间上单调递减 D. 在区间上单调递增
12.若点A的坐标为(3,1),F为抛物线y2=2x的焦点,点P是抛物线上的一动点,则|PA|+|PF|取最小值时点P的坐标为
A. (0,0) B. (1,1) C. (2,2) D. (,1)
13.某几何体三视图如图所示,则该几何体表面积为
A. B.
C. D.
14.已知函数f(x)是(﹣∞,+∞)上的减函数,
那么a的取值范围是
A. (0,1) B. (0,) C. [,) D. (,)
15.若则
A. B. 2 C. D. -2
16.设x,y满足约束条件,目标函数z=ax+by(a>0,b>0)的最大值为2,则的最小值为
A. 5 B. C. D. 9
17.已知非零向量,满足 ,且 ,则与的夹角为( )
A. B. C. D.
18.已知,则( )
A. B. C. D.
19.若函数在上的最大值为4,则的取值范围为( )
A. B. C. D.
20.17世纪德国著名的天文学家开普勒曾经这样说过:“几何学里有两件宝,一个是勾股定理,另一个是黄金分割.如果把勾股定理比作黄金矿的话,那么可以把黄金分割比作钻石矿.”黄金三角形有两种,其中底与腰之比为黄金分割比的黄金三角形被认为是最美的三角形,它是一个顶角为的等腰三角形(另一种是顶角为的等腰三角形).例如,五角星由五个黄金三角形与一个正五边形组成,如图所示,在其中一个黄金中,.根据这些信息,可得( )
A. B. C. D.
二.填空题:本大题共 4 小题,每小题 3 分,共 12 分.
21.函数的最大值是___.
22.函数的值域为________.
23.为满足人民对美好生活的向往,环保部门要求相关企业加强污水治理,排放未达标的企业要限期整改,设企业的污水排放量W与时间t的关系为,用的大小评价在这段时间内企业污水治理能力的强弱,已知整改期内,甲、乙两企业的污水排放量与时间的关系如下图所示.
给出下列四个结论:
①在这段时间内,甲企业的污水治理能力比乙企业强;
②在时刻,甲企业的污水治理能力比乙企业强;
③在时刻,甲、乙两企业的污水排放都已达标;
④甲企业在这三段时间中,在的污水治理能力最强.
其中所有正确结论的序号是____________________.
24.已知函数,对一切,恒成立,则的取值范围是________.
三.解答题:本大题共 4 小题,共 28 分.解答应写出文字说明、证明过程或演算步骤.
25.设函数f(x)=ax-,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
(Ⅰ)求f(x)的解析式;
(Ⅱ)证明:曲线y=f(x)上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,并求此定值.
26.如图,在正四棱柱ABCD-A1B1C1D1中,E为AD中点, F为B1C1中点.
(1)求证:A1F∥平面ECC1;
(2)在CD上是否存在一点G,使BG⊥平面ECC1 若存
在,请确定点G的位置,并证明你的结论;若不存在,请说明理由.
27.某校某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图(已知本次测试成绩满分100分,且均为不低于50分的整数),请根据图表中的信息解答下列问题.
(1)求全班的学生人数及频率分布直方图中分数在[70,80)之间的矩形的高;
(2)为了帮助学生提高数学成绩,决定在班里成立“二帮一”小组,即从成绩[90,100]中选两位同学,共同帮助[50,60)中的某一位同学,已知甲同学的成绩为53分,乙同学的成绩为96分,求甲、乙恰好被安排在同一小组的概率.
28.已知函数f(x)=ax2-xln x.
(1)若f(x)在(0,+∞)上单调递增,求a的取值范围;
(2)若a=e(e为自然对数的底数),证明:当x>0时,f(x)
一、选择题(共 20 小题,每小题 3 分,共 60 分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C D A B A D D C
题号 11 12 13 14 15 16 17 18 19 20
答案 B D D C B C C C C C
填空题(共 4 小题,每小题 3 分,共 12 分)
21.;
22.;
23.①②③;
24..
三、解答题(共 4 小题,共 28 分)
25.(Ⅰ)方程7x-4y-12=0可化为y=x-3.
当x=2时,y=.
又f '(x)=a+,
于是, 解得
故.
(Ⅱ)设P(x0,y0)为曲线上任一点,由y'=1+知曲线在点P(x0,y0)处的切线方程为,
即.
令x=0得y=-,从而得切线与直线x=0的交点坐标为( 0,).
令y=x得y=x=2x0,从而得切线与直线y=x的交点坐标为(2x0,2x0).
所以点P(x0,y0)处的切线与直线x=0,y=x所围成的三角形面积为
故曲线y=f(x)上任一点处的切线与直线x=0,y=x所围成的三角形的面积为定值,此定值为6.
26.
(1)如图,在正四棱柱ABCD-A1B1C1D1中,取BC的中点M,连接AM,FM.
∴B1F∥BM且B1F=BM,
∴四边形B1FMB是平行四边形,
∴FM∥B1B且FM=B1B.
∴FM∥A1A且FM=A1A,
∴四边形AA1FM是平行四边形,
∴FA1∥AM.
∵E为AD中点,
∴AE∥MC且AE=MC,
∴四边形AMCE是平行四边形,
∴CE∥AM,∴CE∥A1F.
∵A1F 平面ECC1,EC 平面ECC1,∴A1F∥平面ECC1.
(2)在CD上存在一点G,使BG⊥平面ECC1,此时G为CD的中点.
取CD的中点G,连接BG,如图D 8-4-9.
∵DE=GC,CD=BC,∠ADC=∠BCD,
∴△CDE≌△BCG, ∴∠ECD=∠GBC.
∵∠CGB+∠GBC=90°,∴∠CGB+∠DCE=90°,∴BG⊥EC.
∵CC1⊥平面ABCD,BG 平面ABCD,
∴CC1⊥BG,又EC∩CC1=C,∴BG⊥平面ECC1.
故在CD上存在中点G,使BG⊥平面ECC1.
27.
【解】(1)由茎叶图知分数在[50,60)上的频数为4,频率为0.008×10=0.08,
故全班的学生人数为50人,
∵分数在[70,80)间的频数为:50﹣(4+14+8+4)=20,
∴频率是,∴矩形的高是0.04.
(2)成绩在[50,60)分数段内的人数有4人,记为甲、A、B、C,成绩在[90,100)分数段内的人数有4人,记为乙、a,b,c,则“二帮一”小组有以下24种分组办法:
甲乙a,甲乙b,甲乙c,甲ab,甲ac,甲bc,A乙a,A乙b,
A乙c,Aab,Aac,Abc,B乙a,B乙b,B乙c,Bab,
Bac,Bbc,C乙a,C乙b,C乙c,Cab,Cac,Cbc,
其中,甲、乙两同学被分在同一小组有3种办法:甲乙a,甲乙b,甲乙c,
∴甲乙两同学恰好被安排在同一小组的概率为P.
28.
(1)f '(x)=2ax-ln x-1.
因为f(x)在(0,+∞)上单调递增,所以当x>0时,f '(x)≥0恒成立,
即2ax-ln x-1≥0恒成立,即2a≥恒成立.
设g(x)=,则2a≥g(x)max.
g'(x)=-,由g'(x)>0,得ln x<0,即0
所以g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
则g(x)max=g(1)=1.
所以2a≥1,即a≥,故a的取值范围是[,+∞).
(2)当a=e时,要证f(x)
设h(x)=ln x+,则h'(x)=(x>0).
由h'(x)<0,得0
设φ(x)=ex-ex(x>0),则φ'(x)=e-ex(x>0).
由φ'(x)>0,得0
因为h(x)和φ(x)不同时为0,所以ln x+>ex-ex,故原不等式成立.
同课章节目录
