2.3.1平面向量基本定理
图片预览




文档简介
课件18张PPT。 dúshūfǎ yǒusāndào xīnyǎnkǒu xìnjiēyào 读书法 有三到 心眼口 信皆要
fāngdúcǐ wùmùbǐ cǐwèizhōng bǐwùqǐ 方读此 勿慕彼 此未终 彼勿起
kuānwéixiàn jǐnyònggōng gōngfūdào zhìsètōng 宽为限 紧用功 工夫到 滞塞通
xīnyǒuyí suízhájì jiùrénwèn qiúquèyì 心有疑 随札记 就人问 求确义
易解:读书的方法要注重三到,眼到、口到、心到,这些都很重要。读着这本书,不要想另一本书,这本书没读完,不要读另一本书。读书计划不妨宽松一些,实际执行时要加紧用功,功夫到了,原先困顿疑惑之处就而然都迎刃而解了。 求学当中,心里有疑问,应随时笔记,一有机会就向良师益友请教,务必确实明白它的真义。(子曰:“敏而好学,不耻下问。” ) 2.3.1平面向量基本定理学习目标:(1)掌握平面向量基本定理;
(2)会运用平面向量基本定理表示平面内任意一个向量;
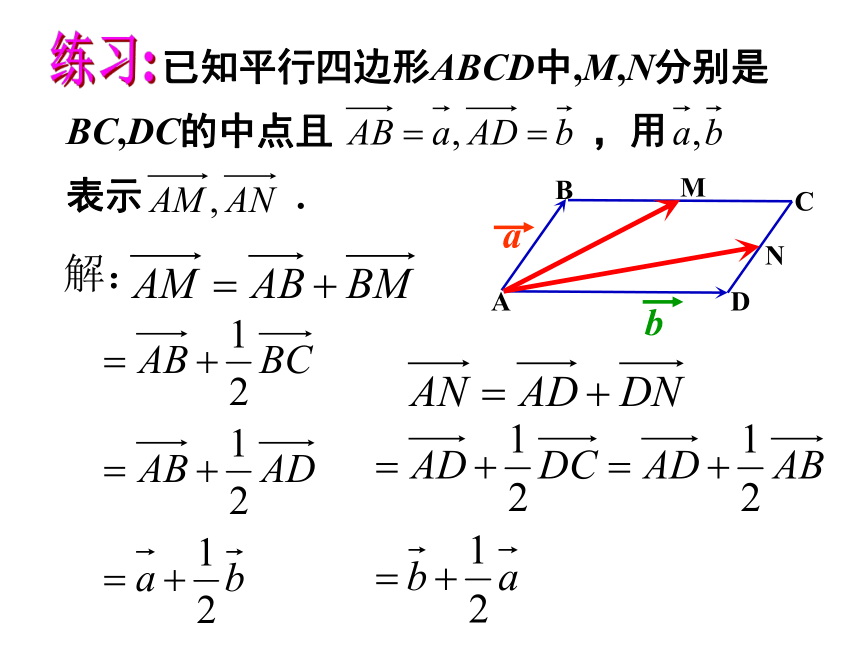
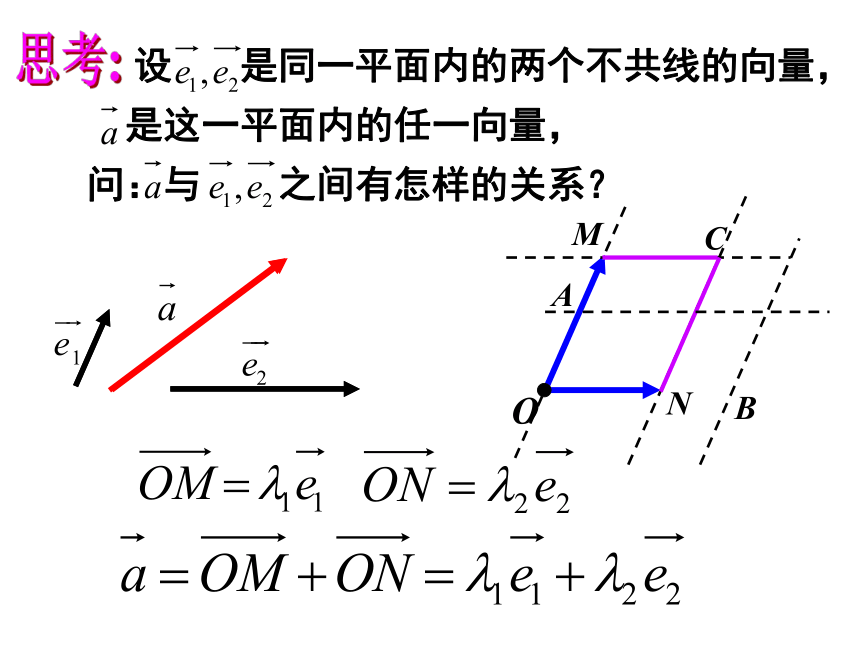
(3)掌握向量夹角的定义及求法. 已知平行四边形ABCD中,M,N分别是BC,DC的中点且 ,用 表示 . 练习:OCABMN思考: 设 是同一平面内的两个不共线的向量,
是这一平面内的任一向量,
问:与 之间有怎样的关系?一、平面向量基本定理:如果 是同一平面内的两个不共线向量,那么对于这一平面内的任一向量 有且只有一对实数 ,使2、基底不唯一,关键是不共线.4、基底给定时,分解形式唯一.说明:
1、把不共线的非零向量 叫做表示这一平面内所有向量的一组基底.3、由定理可将任一向量 在给出基底
的条件下进行分解. 我们学过功的概念,即一个物体在力F的作用下产生位移s(如图)思考:二、向量的夹角
不共线向量有不同方向,它们的位置关系可用夹角来表示。夹角的范围:注意:两向量必须是同起点的结论1:在三角形ABC中M是BC中点G是△ABC重心OBAP结论2:若O, A, B, P在同一平面内A,B,P三点共线不共线化归思想构造思想结论3:结论4:例3:设 是两个不共线向量,已知
若A,B,D三点共线,求实数 ? 化归思想例3:设 是两个不共线向量,已知
若A,B,D三点共线,求实数 ? 构造思想
易解:读书的方法要注重三到,眼到、口到、心到,这些都很重要。读着这本书,不要想另一本书,这本书没读完,不要读另一本书。读书计划不妨宽松一些,实际执行时要加紧用功,功夫到了,原先困顿疑惑之处就而然都迎刃而解了。 求学当中,心里有疑问,应随时笔记,一有机会就向良师益友请教,务必确实明白它的真义。(子曰:“敏而好学,不耻下问。” ) 2.3.1平面向量基本定理学习目标:(1)掌握平面向量基本定理;
(2)会运用平面向量基本定理表示平面内任意一个向量;
(3)掌握向量夹角的定义及求法. 已知平行四边形ABCD中,M,N分别是BC,DC的中点且 ,用 表示 . 练习:OCABMN思考: 设 是同一平面内的两个不共线的向量,
是这一平面内的任一向量,
问:与 之间有怎样的关系?一、平面向量基本定理:如果 是同一平面内的两个不共线向量,那么对于这一平面内的任一向量 有且只有一对实数 ,使2、基底不唯一,关键是不共线.4、基底给定时,分解形式唯一.说明:
1、把不共线的非零向量 叫做表示这一平面内所有向量的一组基底.3、由定理可将任一向量 在给出基底
的条件下进行分解. 我们学过功的概念,即一个物体在力F的作用下产生位移s(如图)思考:二、向量的夹角
不共线向量有不同方向,它们的位置关系可用夹角来表示。夹角的范围:注意:两向量必须是同起点的结论1:在三角形ABC中M是BC中点G是△ABC重心OBAP结论2:若O, A, B, P在同一平面内A,B,P三点共线不共线化归思想构造思想结论3:结论4:例3:设 是两个不共线向量,已知
若A,B,D三点共线,求实数 ? 化归思想例3:设 是两个不共线向量,已知
若A,B,D三点共线,求实数 ? 构造思想
