【课件】3.1.1 函数及其表示方法-第2课时 函数的表示方法 高中数学-RJB-必修第一册-第三章(共28张PPT)
文档属性
| 名称 | 【课件】3.1.1 函数及其表示方法-第2课时 函数的表示方法 高中数学-RJB-必修第一册-第三章(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-05 16:12:44 | ||
图片预览






文档简介
(共28张PPT)
高中数学-RJ·B-必修第一册
3.1.1 函数及其表示方法
第三章 函数
3.1.1 函数及其表示方法
重点:会选择恰当的方法表示函数.
难点:分段函数的简单应用.
1.掌握函数的三种表示法:解析法、图像法、列表法,以及各种表示法的优缺点.
2.在实际问题中,能够选择恰当的表示法来表示函数.
3.能利用函数图像求函数的值域,并确定函数值的变化趋势
4.了解简单的分段函数,会画分段函数的图像,会求分段函数的函数值.
学习目标
知识梳理
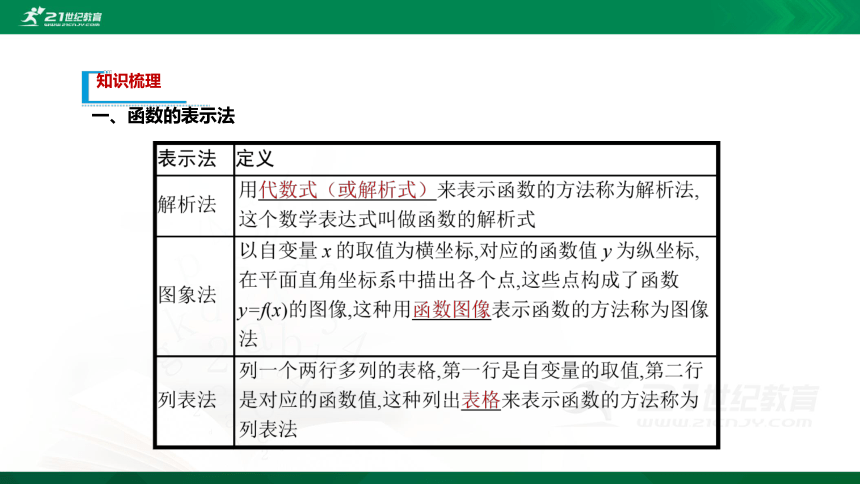
一、函数的表示法
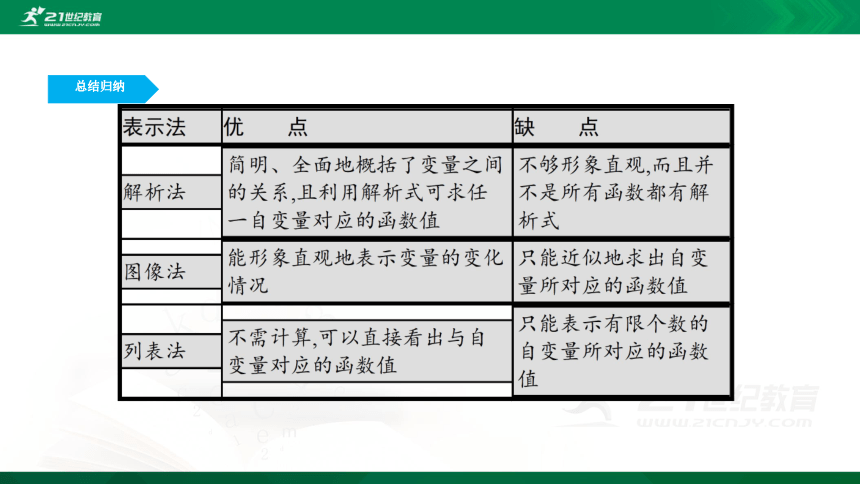
总结归纳
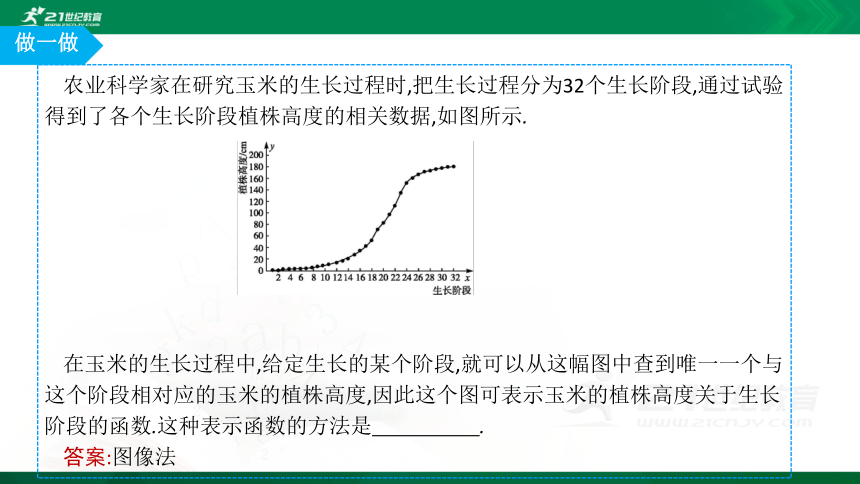
农业科学家在研究玉米的生长过程时,把生长过程分为32个生长阶段,通过试验得到了各个生长阶段植株高度的相关数据,如图所示.
在玉米的生长过程中,给定生长的某个阶段,就可以从这幅图中查到唯一一个与这个阶段相对应的玉米的植株高度,因此这个图可表示玉米的植株高度关于生长阶段的函数.这种表示函数的方法是 .
答案:图像法
做一做
二、分段函数的定义
◎如果一个函数,在其定义域内,
对于自变量的不同取值区间,有不同的对应方式,则称其
为分段函数.
例1
一 用列表法表示函数
常考题型
用列表法将函数f(x)表示如下:
则f(f(2))= .
答案:0
1.已知两个函数f(x)和g(x)的定义域和值域都是集合{1,2,3},其定义如下表:
填写函数f(g(x))的表格,其中三个数依次为 ( )
A.2,1,3 B.1,2,3 C.3,2,1 D.1,3,2
小试牛刀
A
x 1 2 3 x 1 2 3
f(x) 2 3 1 g(x) 1 3 2
x 1 2 3
f[g(x)]
【解析】 因为g(1)=1,所以f(g(1))=f(1)=2;因为g(2)=3,所以f(g(2))=f(3)=1;因为g(3)=2,所以f(g(3))=f(2)=3.
例2
(1)由已知函数定义域为{0,1,2},列表如下:
其图像是离散的点列,如图所示,值域为{1,3,5}.
作出下列函数的图像并求出其值域.
(1)y=2x+1,x∈Z且0≤x≤2;(2)y= ,x∈[2,+∞);(3)y=x2+2x,x∈[-2,2].
【解】
二、函数图像的画法
x 0 1 2
y 1 3 5
2.已知函数y=f(x)的对应关系如下表,
函数y=g(x)的图像是如图所示的曲线ABC,其中A(1,3),B(2,1),C(3,2),
则f(g(2))的值为 ( )
A.3 B.2 C.1 D.0
小试牛刀
B
x 1 2 3
f(x) 2 3 0
例2
(1)由已知函数定义域为{0,1,2},列表如下:
其图象是离散的点列,如图所示,值域为{1,3,5}.
作出下列函数的图像并求出其值域.
(1)y=2x+1,x∈Z且0≤x≤2;(2)y= ,x∈[2,+∞);(3)y=x2+2x,x∈[-2,2].
【解】
二、函数图像的画法
x 0 1 2
y 1 3 5
例2
(2)由已知函数定义域为[2,+∞),列表如下:
其图像是反比例函数y= 图像的一部分,如图所示,
观察图像知函数值域为(0,1].
作出下列函数的图像并求出其值域.
(1)y=2x+1,x∈Z且0≤x≤2;(2)y=,x∈[2,+∞);(3)y=x2+2x,x∈[-2,2].
【解】
二、函数图像的画法
x 2 3 4 5 …
y 1 …
例2
(3)由已知函数定义域为[-2,2],列表如下:
不能其图像是抛物线y=x2+2x在-2≤x≤2之间的部分,如图所示,
由图像可得函数的值域是[-1,8].
作出下列函数的图像并求出其值域.
(1)y=2x+1,x∈Z且0≤x≤2;(2)y= ,x∈[2,+∞);(3)y=x2+2x,x∈[-2,2].
【解】
二、函数图像的画法
x -2 -1 0 1 2
y 0 -1 0 3 8
1.作出下列函数的图像.
(1)y=;(2)y=|x2-2x|+1.
【解】(1)∵ y==2+,∴ 先作函数y= 的图像,把它向右平移1个单位长度得到函数y=的图像,再把平移后的图像向上平移2个单位长度得到函数y=的图像,如图所示.
小试牛刀
2.画出函数y=-2x+1,x∈[0,2]的图像,并根据图像写出函数的值域.
【解】函数y=-2x+1,x∈[0,2]的图像如图所示,
由图像可知,y=-2x+1,x∈[0,2]的值域为[-3,1].
小试牛刀
作函数图像时需注意的六个问题
1.先确定函数的定义域,要在定义域内作图;
2.图像是实线或实点,定义域外的部分有时可用虚线来衬托整个图像;
3.要标出某些关键点,例如图像的顶点、端点、与坐标轴的交点;
4.要作y=|g(x)|的图像,可先作y=g(x)的图像,然后x轴及x轴上方的部分保持不变,
将x轴下方的部分沿x轴翻折上去即可.
5.要作y=g(|x|)的图像,可先作 y=g(x)的图像,然后y轴及y轴右侧的部分保持不变,将轴右侧的部分图像沿y轴翻折过去即可.
6.一般地,函数y=|x-a|的图像关于直线x=a对称.
解题归纳
例3
三 灵活应用三种方法表示函数
某商场新进了10台彩电,每台售价3 000元,试求销售额y与售出台数x之间的函数关系,分别用列表法、图像法、解析法表示出来.
【解】
(2)图像法:如图所示.
(3)解析法:y=3 000x,x∈{1,2,3,…,10}.
(1)列表法如下.
x/台 1 2 3 4 5
y/元 3 000 6 000 9 000 12 000 15 000
x/台 6 7 8 9 10
y/元 18 000 21 000 24 000 27 000 30 000
例4
四 图像的识别
如图所示的4个图像中,与所给的3个事件吻合最好的顺序为 ( )
①我离开学校不久后,发现把作业本忘在教室,于是立刻返回教室里取了作业本再回家;
②我放学回家骑着车一路匀速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
③我放学从学校出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.
(1) (2) (3) (4)
A.(1)(2)(4) B.(4)(1)(2)
C.(4)(1)(3) D.(4)(2)(3)
B
【解析】
①根据回学校后,离学校的距离又变为0,可判断①的图像开始后不久又回归为0,与(4)吻合;
②由途中遇到一次交通堵塞,可判断中间有一段函数值没有发生变化,与(1)吻合;
③由为了赶时间开始加速,可判断函数的图像上升速度越来越快,与(2)吻合.
综上,所给4个图像中,与所给的3个事件吻合最好的顺序为(4)(1)(2).故选B.
如图,△ABC为等腰直角三角形,直线l与AB相交且l⊥AB,若直线l截这个三角形所得的位于直线右侧的图形面积为y,点A到直线l的距离为x,则y=f(x)的图像大致为 ( )
A B C D
小试牛刀
C
(1)首先在阅读材料、理解题意的基础上,把实际问题抽象为函数问题.
(2)利用函数知识建立相应的函数模型.
(3)再利用函数知识对函数模型进行分析、研究,得出数学结论.
(4)最后把数学结论(结果)应用到实际问题中.
解题归纳
五、 与分段函数有关的实际问题
例5
由于某海域水污染严重,为了获得第一手的水文资料,潜水员需要潜入水深为60米的水底进行作业.根据经验,潜水员下潜的平均速度为v米/单位时间,每单位时间消耗氧气 升,在水底作业10个单位时间,每单位时间消耗氧气0.9升,返回水面的平均速度为米/单位时间,每单位时间消耗氧气1.5升,记该潜水员完成此次任务的消耗氧气总量为y升.求y关于v的函数关系式.
由题意得,下潜过程用时单位时间,消耗氧气 ×= (升),
水底作业过程中消耗氧气10×0.9=9(升),
返回水面过程用时=(单位时间),消耗氧气×1.5=(升),
∴ 消耗氧气总量y=++9+= (v>0)(升).
【解】
求实际问题中函数的解析式,关键是充分利用条件建立关于变量的等式.
确定函数的定义域时,除了考虑函数解析式自身的限制条件外,还要考虑问题的实际意义.
解题归纳
小结
两个知识点:
1.函数的表示方法(图像法、解析法、列表法);2.分段函数的定义.
五种题型:
1.用列表法表示函数;
2.函数图像的画法;
3.灵活应用方法表示函数;
4.图像的识别;
5.与分段函数有关的实际问题.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
高中数学-RJ·B-必修第一册
3.1.1 函数及其表示方法
第三章 函数
3.1.1 函数及其表示方法
重点:会选择恰当的方法表示函数.
难点:分段函数的简单应用.
1.掌握函数的三种表示法:解析法、图像法、列表法,以及各种表示法的优缺点.
2.在实际问题中,能够选择恰当的表示法来表示函数.
3.能利用函数图像求函数的值域,并确定函数值的变化趋势
4.了解简单的分段函数,会画分段函数的图像,会求分段函数的函数值.
学习目标
知识梳理
一、函数的表示法
总结归纳
农业科学家在研究玉米的生长过程时,把生长过程分为32个生长阶段,通过试验得到了各个生长阶段植株高度的相关数据,如图所示.
在玉米的生长过程中,给定生长的某个阶段,就可以从这幅图中查到唯一一个与这个阶段相对应的玉米的植株高度,因此这个图可表示玉米的植株高度关于生长阶段的函数.这种表示函数的方法是 .
答案:图像法
做一做
二、分段函数的定义
◎如果一个函数,在其定义域内,
对于自变量的不同取值区间,有不同的对应方式,则称其
为分段函数.
例1
一 用列表法表示函数
常考题型
用列表法将函数f(x)表示如下:
则f(f(2))= .
答案:0
1.已知两个函数f(x)和g(x)的定义域和值域都是集合{1,2,3},其定义如下表:
填写函数f(g(x))的表格,其中三个数依次为 ( )
A.2,1,3 B.1,2,3 C.3,2,1 D.1,3,2
小试牛刀
A
x 1 2 3 x 1 2 3
f(x) 2 3 1 g(x) 1 3 2
x 1 2 3
f[g(x)]
【解析】 因为g(1)=1,所以f(g(1))=f(1)=2;因为g(2)=3,所以f(g(2))=f(3)=1;因为g(3)=2,所以f(g(3))=f(2)=3.
例2
(1)由已知函数定义域为{0,1,2},列表如下:
其图像是离散的点列,如图所示,值域为{1,3,5}.
作出下列函数的图像并求出其值域.
(1)y=2x+1,x∈Z且0≤x≤2;(2)y= ,x∈[2,+∞);(3)y=x2+2x,x∈[-2,2].
【解】
二、函数图像的画法
x 0 1 2
y 1 3 5
2.已知函数y=f(x)的对应关系如下表,
函数y=g(x)的图像是如图所示的曲线ABC,其中A(1,3),B(2,1),C(3,2),
则f(g(2))的值为 ( )
A.3 B.2 C.1 D.0
小试牛刀
B
x 1 2 3
f(x) 2 3 0
例2
(1)由已知函数定义域为{0,1,2},列表如下:
其图象是离散的点列,如图所示,值域为{1,3,5}.
作出下列函数的图像并求出其值域.
(1)y=2x+1,x∈Z且0≤x≤2;(2)y= ,x∈[2,+∞);(3)y=x2+2x,x∈[-2,2].
【解】
二、函数图像的画法
x 0 1 2
y 1 3 5
例2
(2)由已知函数定义域为[2,+∞),列表如下:
其图像是反比例函数y= 图像的一部分,如图所示,
观察图像知函数值域为(0,1].
作出下列函数的图像并求出其值域.
(1)y=2x+1,x∈Z且0≤x≤2;(2)y=,x∈[2,+∞);(3)y=x2+2x,x∈[-2,2].
【解】
二、函数图像的画法
x 2 3 4 5 …
y 1 …
例2
(3)由已知函数定义域为[-2,2],列表如下:
不能其图像是抛物线y=x2+2x在-2≤x≤2之间的部分,如图所示,
由图像可得函数的值域是[-1,8].
作出下列函数的图像并求出其值域.
(1)y=2x+1,x∈Z且0≤x≤2;(2)y= ,x∈[2,+∞);(3)y=x2+2x,x∈[-2,2].
【解】
二、函数图像的画法
x -2 -1 0 1 2
y 0 -1 0 3 8
1.作出下列函数的图像.
(1)y=;(2)y=|x2-2x|+1.
【解】(1)∵ y==2+,∴ 先作函数y= 的图像,把它向右平移1个单位长度得到函数y=的图像,再把平移后的图像向上平移2个单位长度得到函数y=的图像,如图所示.
小试牛刀
2.画出函数y=-2x+1,x∈[0,2]的图像,并根据图像写出函数的值域.
【解】函数y=-2x+1,x∈[0,2]的图像如图所示,
由图像可知,y=-2x+1,x∈[0,2]的值域为[-3,1].
小试牛刀
作函数图像时需注意的六个问题
1.先确定函数的定义域,要在定义域内作图;
2.图像是实线或实点,定义域外的部分有时可用虚线来衬托整个图像;
3.要标出某些关键点,例如图像的顶点、端点、与坐标轴的交点;
4.要作y=|g(x)|的图像,可先作y=g(x)的图像,然后x轴及x轴上方的部分保持不变,
将x轴下方的部分沿x轴翻折上去即可.
5.要作y=g(|x|)的图像,可先作 y=g(x)的图像,然后y轴及y轴右侧的部分保持不变,将轴右侧的部分图像沿y轴翻折过去即可.
6.一般地,函数y=|x-a|的图像关于直线x=a对称.
解题归纳
例3
三 灵活应用三种方法表示函数
某商场新进了10台彩电,每台售价3 000元,试求销售额y与售出台数x之间的函数关系,分别用列表法、图像法、解析法表示出来.
【解】
(2)图像法:如图所示.
(3)解析法:y=3 000x,x∈{1,2,3,…,10}.
(1)列表法如下.
x/台 1 2 3 4 5
y/元 3 000 6 000 9 000 12 000 15 000
x/台 6 7 8 9 10
y/元 18 000 21 000 24 000 27 000 30 000
例4
四 图像的识别
如图所示的4个图像中,与所给的3个事件吻合最好的顺序为 ( )
①我离开学校不久后,发现把作业本忘在教室,于是立刻返回教室里取了作业本再回家;
②我放学回家骑着车一路匀速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
③我放学从学校出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.
(1) (2) (3) (4)
A.(1)(2)(4) B.(4)(1)(2)
C.(4)(1)(3) D.(4)(2)(3)
B
【解析】
①根据回学校后,离学校的距离又变为0,可判断①的图像开始后不久又回归为0,与(4)吻合;
②由途中遇到一次交通堵塞,可判断中间有一段函数值没有发生变化,与(1)吻合;
③由为了赶时间开始加速,可判断函数的图像上升速度越来越快,与(2)吻合.
综上,所给4个图像中,与所给的3个事件吻合最好的顺序为(4)(1)(2).故选B.
如图,△ABC为等腰直角三角形,直线l与AB相交且l⊥AB,若直线l截这个三角形所得的位于直线右侧的图形面积为y,点A到直线l的距离为x,则y=f(x)的图像大致为 ( )
A B C D
小试牛刀
C
(1)首先在阅读材料、理解题意的基础上,把实际问题抽象为函数问题.
(2)利用函数知识建立相应的函数模型.
(3)再利用函数知识对函数模型进行分析、研究,得出数学结论.
(4)最后把数学结论(结果)应用到实际问题中.
解题归纳
五、 与分段函数有关的实际问题
例5
由于某海域水污染严重,为了获得第一手的水文资料,潜水员需要潜入水深为60米的水底进行作业.根据经验,潜水员下潜的平均速度为v米/单位时间,每单位时间消耗氧气 升,在水底作业10个单位时间,每单位时间消耗氧气0.9升,返回水面的平均速度为米/单位时间,每单位时间消耗氧气1.5升,记该潜水员完成此次任务的消耗氧气总量为y升.求y关于v的函数关系式.
由题意得,下潜过程用时单位时间,消耗氧气 ×= (升),
水底作业过程中消耗氧气10×0.9=9(升),
返回水面过程用时=(单位时间),消耗氧气×1.5=(升),
∴ 消耗氧气总量y=++9+= (v>0)(升).
【解】
求实际问题中函数的解析式,关键是充分利用条件建立关于变量的等式.
确定函数的定义域时,除了考虑函数解析式自身的限制条件外,还要考虑问题的实际意义.
解题归纳
小结
两个知识点:
1.函数的表示方法(图像法、解析法、列表法);2.分段函数的定义.
五种题型:
1.用列表法表示函数;
2.函数图像的画法;
3.灵活应用方法表示函数;
4.图像的识别;
5.与分段函数有关的实际问题.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
