【课件】3.1.2 函数的单调性-第1课时 高中数学-RJB-必修第一册-第三章(共24张PPT)
文档属性
| 名称 | 【课件】3.1.2 函数的单调性-第1课时 高中数学-RJB-必修第一册-第三章(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-05 16:19:07 | ||
图片预览








文档简介
(共24张PPT)
数学-RJB-必修第一册
3.1.2 函数的单调性
第1课时
第三章 函数的概念与性质
重点:理解函数单调性的概念;判断函数的单调性.
难点:判断函数的单调性.
1.了解函数的单调区间、单调性等概念.
2.会划分函数的单调区间,判断单调性.
3.会用定义证明函数的单调性.
学习目标
知识梳理
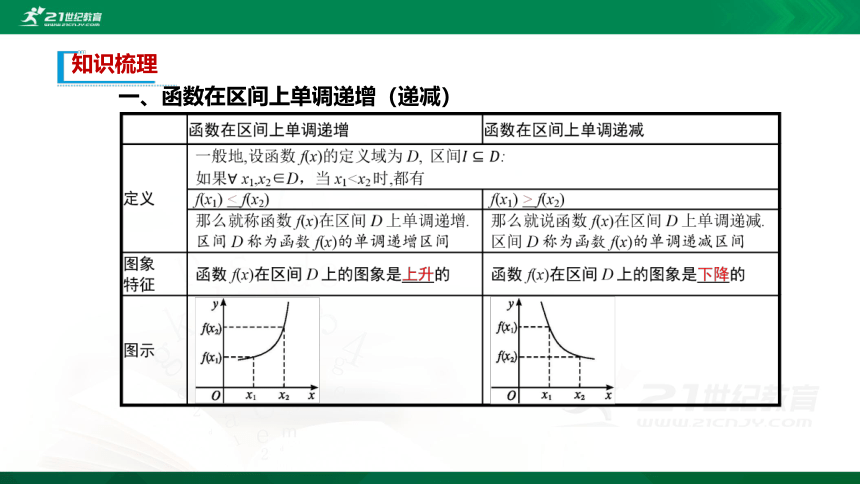
一、函数在区间上单调递增(递减)
总结归纳
1.函数f(x)在区间D上是增函数,x1,x2∈D,且x1≠x2
(x1-x2)[f(x1)-f(x2)]>0
2.函数f(x)在区间D上是减函数,x1,x2∈D,且x1≠x2
(x1-x2)[f(x1)-f(x2)]<0
特别提醒
函数在区间上单调递增(递减)的定义是用数学符号来刻画函数的图象特征,它反映了函数图象的变化趋势(当自变量增大时,函数值是增大还是减小,图象是上升还是下降);函数y=f(x)在区间D上是单调递增(递减),等价于对于D中任意的两个自变量x1,x2,且x1f(x2));其中“任意”二字是关键,不能用具体的两个自变量代替,否则就会产生错误.比如函数f(x)取x1=-1,x2=1,f(x1)=-1,f(x2)=1,f(x1)【做一做1-1】 已知函数f(x)的图象如图所示,则( )
A.函数f(x)在区间[-1,2]上是增函数
B.函数f(x)在区间[-1,2]上是减函数
C.函数f(x)在区间[-1,4]上是减函数
D.函数f(x)在区间[2,4]上是增函数
答案:A
【做一做1-2】 已知函数y=f(x)在区间(a,b)内是单调递减,x1,x2∈(a,b),且x1A.f(x1)f(x2)
C.f(x1)=f(x2) D.以上都有可能
答案:B
二、函数的增减性
1.定义:如果函数y=f(x)在区间I上单调递增或单调递减,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间I叫做y=f(x)的单调区间.
2.图象特征:函数y=f(x)在区间I上具有单调性,则函数y=f(x)在区间I上的图象是上升的或下降的.
总结归纳
基本初等函数的单调区间如下表所示:
【做一做2】已知[0,3]是函数f(x)定义域内的一个区间,若f(1)A.是单调递增 B.是单调递减
C.不单调递增就是单调递减 D.增减性不能确定
解析:虽然1,2∈[0,3],1<2,且f(1)答案:D
例1
一 利用图象确定函数的单调区间
常考题型
已知函数f(x)=-x2+2|x|+3.
(1)用分段函数的形式表示f(x); (2)画出f(x)的图象;
(3)根据图象写出f(x)的单调区间.
【分析】
(1)当x≥0时,f(x)=-x2+2x+3=-(x-1)2+4;
当x<0时,f(x)=-x2-2x+3=-(x+1)2+4,
即f(x)
(1)需要讨论x≥0和x<0两种情况; (2)利用画分段函数图象的步骤画出;
(3)借助函数图象写出单调区间.
【解】
例1
一 利用图象确定函数的单调区间
常考题型
已知函数f(x)=-x2+2|x|+3.
(1)用分段函数的形式表示f(x); (2)画出f(x)的图象;
(3)根据图象写出f(x)的单调区间.
【分析】
(1)需要讨论x≥0和x<0两种情况; (2)利用画分段函数图象的步骤画出;
(3)借助函数图象写出单调区间.
【解】
(2)函数f(x)的图象如图所示.
例1
一 利用图象确定函数的单调区间
常考题型
已知函数f(x)=-x2+2|x|+3.
(1)用分段函数的形式表示f(x); (2)画出f(x)的图象;
(3)根据图象写出f(x)的单调区间.
【分析】
(1)需要讨论x≥0和x<0两种情况; (2)利用画分段函数图象的步骤画出;
(3)借助函数图象写出单调区间.
【解】
(3)函数f(x)的图象在区间(-∞,-1]和[0,1]上是上升的,
在区间(-1,0)和(1,+∞)内是下降的,
所以f(x)的单调递增区间是(-∞,-1],[0,1],单调递减区间是[-1,0],[1,+∞).
1.对于基本初等函数≠0),常借助函数图象去探求函数的单调区间.
2.对于含有绝对值的函数,往往要转化成分段函数,画出其图象,借助图象的变化趋势分析函数的单调性(区间).
解题归纳
1.已知函数f(x)则的单调递增区间是单调递减区间是
小试牛刀
【解析】画出f(x)的图象如图所示,
可知f(x)在区间(-∞,0]和[1,+∞)上都是增函数,在(0,1)上是减函数.
【答案】 (- ∞,0],[1,+∞) (0,1)
例2
设x1,x2是区间(0,1)内的任意两个实数,且x1则f(x1)-f(x2)
=(x1-x2)
∵0∴x1x2-1<0,x1-x2<0,x1x2>0.
∴f(x)=x(0,1)内是减函数.
∴f(x1)-f(x2)>0,即f(x1)>f(x2).
求证:函数f(x)=x
【证明】
二、证明函数的单调性
例3
三、函数单调性的应用
已知函数f(x)的定义域为[-2,2],且f(x)在区间[-2,2]上是增函数,
f(1-m)【分析】利用单调性将函数值的大小关系转化为自变量的大小关系,即脱去符号f,转化为关于m的一元一次不等式组,解出m的取值范围.
【解】因为f(x)在区间[-2,2]上单调递增,且f(1-m)解题归纳
1.利用函数的单调性可以比较函数值或自变量的大小.在解决比较函数值大小的问题时,要注意将对应的自变量转化到同一个单调区间上.需要注意的是,不要忘记函数的定义域.
2.(1)若f(x)在区间D上是增函数,x1,x2是区间D内的任意两个实数,则f(x1)>f(x2) x1>x2;f(x1)(2)若f(x)在区间D上是减函数,x1,x2是区间D内的任意两个实数,则f(x1)>f(x2) x1x2.
小试牛刀
已知函数y=f(x)是区间(-∞,+∞)内的增函数,且f(2x-3)>f(5x+6),求实数x的取值范围.
【解】由题意知2x-3>5x+6,
解得x<-3.
故实数x的取值范围是(-∞,-3).
小结
两个知识点:
1.函数在区间上单调递增(递减);2.函数的增减性;
三种题型:
1.利用图象确定函数的单调区间;
2.证明函数的单调性;
3.函数单调性的应用.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学-RJB-必修第一册
3.1.2 函数的单调性
第1课时
第三章 函数的概念与性质
重点:理解函数单调性的概念;判断函数的单调性.
难点:判断函数的单调性.
1.了解函数的单调区间、单调性等概念.
2.会划分函数的单调区间,判断单调性.
3.会用定义证明函数的单调性.
学习目标
知识梳理
一、函数在区间上单调递增(递减)
总结归纳
1.函数f(x)在区间D上是增函数,x1,x2∈D,且x1≠x2
(x1-x2)[f(x1)-f(x2)]>0
2.函数f(x)在区间D上是减函数,x1,x2∈D,且x1≠x2
(x1-x2)[f(x1)-f(x2)]<0
特别提醒
函数在区间上单调递增(递减)的定义是用数学符号来刻画函数的图象特征,它反映了函数图象的变化趋势(当自变量增大时,函数值是增大还是减小,图象是上升还是下降);函数y=f(x)在区间D上是单调递增(递减),等价于对于D中任意的两个自变量x1,x2,且x1
A.函数f(x)在区间[-1,2]上是增函数
B.函数f(x)在区间[-1,2]上是减函数
C.函数f(x)在区间[-1,4]上是减函数
D.函数f(x)在区间[2,4]上是增函数
答案:A
【做一做1-2】 已知函数y=f(x)在区间(a,b)内是单调递减,x1,x2∈(a,b),且x1
C.f(x1)=f(x2) D.以上都有可能
答案:B
二、函数的增减性
1.定义:如果函数y=f(x)在区间I上单调递增或单调递减,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间I叫做y=f(x)的单调区间.
2.图象特征:函数y=f(x)在区间I上具有单调性,则函数y=f(x)在区间I上的图象是上升的或下降的.
总结归纳
基本初等函数的单调区间如下表所示:
【做一做2】已知[0,3]是函数f(x)定义域内的一个区间,若f(1)
C.不单调递增就是单调递减 D.增减性不能确定
解析:虽然1,2∈[0,3],1<2,且f(1)
例1
一 利用图象确定函数的单调区间
常考题型
已知函数f(x)=-x2+2|x|+3.
(1)用分段函数的形式表示f(x); (2)画出f(x)的图象;
(3)根据图象写出f(x)的单调区间.
【分析】
(1)当x≥0时,f(x)=-x2+2x+3=-(x-1)2+4;
当x<0时,f(x)=-x2-2x+3=-(x+1)2+4,
即f(x)
(1)需要讨论x≥0和x<0两种情况; (2)利用画分段函数图象的步骤画出;
(3)借助函数图象写出单调区间.
【解】
例1
一 利用图象确定函数的单调区间
常考题型
已知函数f(x)=-x2+2|x|+3.
(1)用分段函数的形式表示f(x); (2)画出f(x)的图象;
(3)根据图象写出f(x)的单调区间.
【分析】
(1)需要讨论x≥0和x<0两种情况; (2)利用画分段函数图象的步骤画出;
(3)借助函数图象写出单调区间.
【解】
(2)函数f(x)的图象如图所示.
例1
一 利用图象确定函数的单调区间
常考题型
已知函数f(x)=-x2+2|x|+3.
(1)用分段函数的形式表示f(x); (2)画出f(x)的图象;
(3)根据图象写出f(x)的单调区间.
【分析】
(1)需要讨论x≥0和x<0两种情况; (2)利用画分段函数图象的步骤画出;
(3)借助函数图象写出单调区间.
【解】
(3)函数f(x)的图象在区间(-∞,-1]和[0,1]上是上升的,
在区间(-1,0)和(1,+∞)内是下降的,
所以f(x)的单调递增区间是(-∞,-1],[0,1],单调递减区间是[-1,0],[1,+∞).
1.对于基本初等函数≠0),常借助函数图象去探求函数的单调区间.
2.对于含有绝对值的函数,往往要转化成分段函数,画出其图象,借助图象的变化趋势分析函数的单调性(区间).
解题归纳
1.已知函数f(x)则的单调递增区间是单调递减区间是
小试牛刀
【解析】画出f(x)的图象如图所示,
可知f(x)在区间(-∞,0]和[1,+∞)上都是增函数,在(0,1)上是减函数.
【答案】 (- ∞,0],[1,+∞) (0,1)
例2
设x1,x2是区间(0,1)内的任意两个实数,且x1
=(x1-x2)
∵0
∴f(x)=x(0,1)内是减函数.
∴f(x1)-f(x2)>0,即f(x1)>f(x2).
求证:函数f(x)=x
【证明】
二、证明函数的单调性
例3
三、函数单调性的应用
已知函数f(x)的定义域为[-2,2],且f(x)在区间[-2,2]上是增函数,
f(1-m)
【解】因为f(x)在区间[-2,2]上单调递增,且f(1-m)
1.利用函数的单调性可以比较函数值或自变量的大小.在解决比较函数值大小的问题时,要注意将对应的自变量转化到同一个单调区间上.需要注意的是,不要忘记函数的定义域.
2.(1)若f(x)在区间D上是增函数,x1,x2是区间D内的任意两个实数,则f(x1)>f(x2) x1>x2;f(x1)
小试牛刀
已知函数y=f(x)是区间(-∞,+∞)内的增函数,且f(2x-3)>f(5x+6),求实数x的取值范围.
【解】由题意知2x-3>5x+6,
解得x<-3.
故实数x的取值范围是(-∞,-3).
小结
两个知识点:
1.函数在区间上单调递增(递减);2.函数的增减性;
三种题型:
1.利用图象确定函数的单调区间;
2.证明函数的单调性;
3.函数单调性的应用.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
