【课件】3.1.3 函数的奇偶性 高中数学-RJB-必修第一册-第三章(共28张PPT)
文档属性
| 名称 | 【课件】3.1.3 函数的奇偶性 高中数学-RJB-必修第一册-第三章(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-05 16:30:48 | ||
图片预览








文档简介
(共28张PPT)
数学-RJB-必修第一册
3.1.3 函数的奇偶性
第三章 函数
学习目标
1.结合具体函数,了解函数奇偶性的含义.
2.掌握偶函数的图像关于y轴对称、奇函数的图像关于原点对称的特性.
3.掌握奇函数在关于原点对称的两个区间上具有相同的单调性、偶函数在关于原点对称的两个区间上具有相反的单调性的特性.
重点:函数奇偶性的含义,判断函数的奇偶性.
难点:函数奇偶性的应用.
知识梳理
1.偶函数和奇函数
名师点拨
1.奇函数和偶函数的定义中的“任意”是指定义域中所有的实数;因为-x与x同时属于定义域,即具有奇偶性的函数的定义域关于原点对称.
2.函数f(x)是偶函数 对定义域内任意一个x,有f(-x)-f(x)=0 f(x)的图像关于y轴对称.
3.函数f(x)是奇函数 对定义域内任意一个x,有f(-x)+f(x)=0 f(x)的图像关于原点对称.
【做一做1-1】
若函数y=f(x),x∈[-1,a](a>-1)是奇函数,则a等于( )
A.-1 B.0 C.1 D.无法确定
答案:C
【做一做1-2】
下列函数是偶函数的是( )
A.y=2x B.y=2x2+3
解析:由偶函数的定义知,y=2x2+3是偶函数.
答案:B
2.奇偶性
归纳总结
基本函数的奇偶性如下:
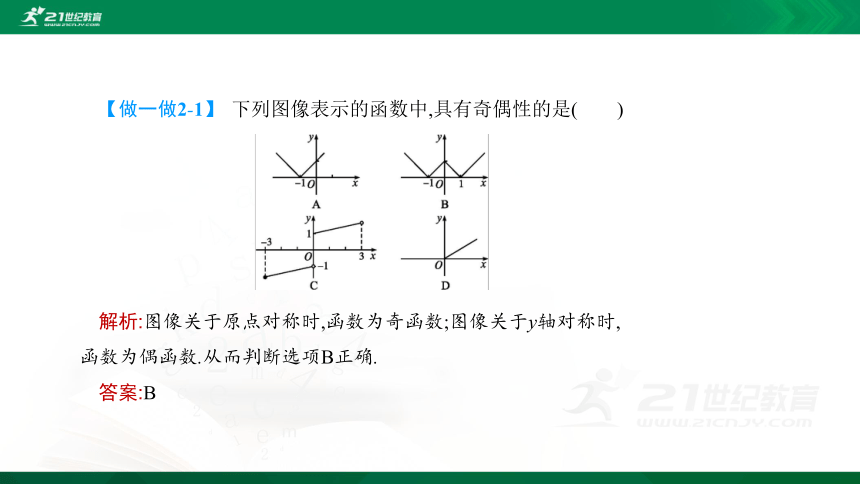
【做一做2-1】 下列图像表示的函数中,具有奇偶性的是( )
解析:图像关于原点对称时,函数为奇函数;图像关于y轴对称时,函数为偶函数.从而判断选项B正确.
答案:B
【做一做2-2】 若函数f(x)=x2-2mx+4是偶函数,则实数m= .
答案:0
剖析
理解函数的奇偶性
函数f(x)的奇偶性的定义是用f(-x)=±f(x)来刻画函数f(x)的图像的特征(图象关于原点或y轴对称)的;函数的奇偶性是对于函数的整个定义域来说的,这一点与函数的单调性不同.从这个意义上来讲,函数的单调性是函数的局部性质,而奇偶性是函数的整体性质.只有对函数f(x)的定义域内的每一个值x,都有f(-x)=f(x)或f(-x)=-f(x),才能说f(x)为偶函数或奇函数;定义中要求“对于函数f(x)的定义域内任意一个自变量x,都有f(-x)=f(x)或f(-x)=-f(x)”成立,其前提为f(-x)和f(x)都有意义,所以-x也属于f(x)的定义域,即自变量x的取值范围要关于原点对称,于是奇(偶)函数的定义域是一个关于原点对称的数集,这是函数存在奇偶性的前提.例如将函数f(x)=x2+1,f(x)=x的定义域分别限定为(0,+∞)与(-3,3],则它们都为非奇非偶函数;函数奇偶性的定义中的等式f(-x)=-f(x)(或f(-x)=f(x))是其定义域上的恒等式,而不是对部分x成立.
尽管当|x|≤1时,都有f(-x)=f(x),但当|x|>1时,f(-x)≠f(x),所以它不是偶函数.
常考题型
一、判断函数的奇偶性
【例1】 判断下列函数的奇偶性:
分析:先求出定义域,再判断f(-x)与f(x)的关系.
解:(1)因为函数的定义域为{x|x≠-1},不关于原点对称,所以f(x)既不是奇函数又不是偶函数.
(2)因为函数的定义域为R,关于原点对称,
f(-x)=(-x)3-2(-x)=2x-x3=-f(x),所以f(x)是奇函数.
(3)因为函数的定义域为R,关于原点对称,
所以f(x)是偶函数.
【变式训练1】 判断下列函数的奇偶性:
(1)f(x)=x2+1,x∈[-2,2);(2)f(x)=|x-1|+|x+1|;(3)f(x)=0,x∈R.
解:(1)∵f(x)的定义域[-2,2)不关于原点对称,
∴f(x)既不是奇函数又不是偶函数.
(2)f(x)的定义域为R,关于原点对称,
又f(-x)=|-x-1|+|-x+1|=|x+1|+|x-1|=f(x),
∴f(x)为偶函数.
(3)∵f(x)=0,x∈R,
∴f(-x)=f(x),且f(-x)=-f(x),
∴f(x)既是奇函数又是偶函数.
二、奇(偶)函数的图像问题
分析:先证明f(x)是偶函数,再依据其图像关于y轴对称作图.
则f(x)的图像关于y轴对称,其图像如图所示.
解题归纳
利用函数的奇偶性作图,其依据是奇函数的图像关于原点对称,偶函数的图像关于y轴对称.
【变式训练2】 已知奇函数f(x)的定义域为[-5,5],其y轴右侧图像如图所示,写出使f(x)>0的x的取值集合.
解:由于f(x)为奇函数,y轴右侧图像已知,结合奇函数图象关于原点对称,作出y轴左侧图像,如图所示,由图像知,当x∈(0,2)时,f(x)>0;当x∈(-5,-2)时,f(x)>0,所以使f(x)>0的x的取值集合为(-5,-2)∪(0,2).
三、利用函数的奇偶性求参数
【例3】 已知函数f(x)=(x+a)(x-4)为偶函数,则实数a= .
解析:因为函数f(x)为偶函数,所以f(-x)=f(x),即(-x+a)(-x-4) =(x+a)(x-4),即x2+(4-a)x-4a=x2-(4-a)x-4a,故4-a=-(4-a),解得a=4.
答案:4
反思
利用函数奇偶性求参数值的常见类型及求解策略:
(1)定义域含参数:奇(偶)函数f(x)的定义域为[a,b],根据定义域关于原点对称,可以利用a+b=0求参数.
(2)解析式含参数:根据f(-x)=-f(x)或f(-x)=f(x)列式,比较系数可解.
【变式训练3】 若函数f(x)=ax2+bx+3a+b是偶函数,定义域为[a-1,2a],则a= ,b= .
解析:因为偶函数的定义域关于原点对称,所以a-1=-2a,
结合偶函数图像的特点,易得b=0.
四、利用函数的奇偶性求函数的解析式
【例4】 若f(x)是定义在R上的奇函数,当x<0时,f(x)=x(1-x),求函数f(x)的解析式.
解:∵f(x)是定义在R上的奇函数,∴f(-x)=-f(x).当x>0时,-x<0,
∴f(x)=-f(-x)=x(1+x).
当x=0时,f(-0)=-f(0),即f(0)=-f(0),∴f(0)=0.
反思
1.若f(x)是奇函数,且f(0)有意义,则f(0)=0;
2.已知函数的奇偶性和函数在某区间上的解析式,求该函数在与已知区间关于原点对称的区间上的解析式时,首先设出所求区间上的自变量,利用奇、偶函数的定义域关于原点对称的特点,把它转化到已知解析式的区间上,代入已知的解析式,然后再次利用函数的奇偶性求解即可.
【变式训练4】 已知f(x)是R上的偶函数,当x∈(0,+∞)时,f(x)=x2+x-1,求当x∈(-∞,0)时,f(x)的解析式.
解:设x<0,则-x>0.
∴f(-x)=(-x)2+(-x)-1=x2-x-1.
∵函数f(x)是偶函数,∴f(-x)=f(x).
∴当x∈(-∞,0)时,f(x)=x2-x-1.
小结
两个知识点:
1.偶函数和奇函数 ;2.奇偶性.
四种题型:
1.判断函数的奇偶性;
2.奇(偶)函数的图像问题;
3.利用函数的奇偶性求参数;
4.利用函数的奇偶性求函数的解析式.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学-RJB-必修第一册
3.1.3 函数的奇偶性
第三章 函数
学习目标
1.结合具体函数,了解函数奇偶性的含义.
2.掌握偶函数的图像关于y轴对称、奇函数的图像关于原点对称的特性.
3.掌握奇函数在关于原点对称的两个区间上具有相同的单调性、偶函数在关于原点对称的两个区间上具有相反的单调性的特性.
重点:函数奇偶性的含义,判断函数的奇偶性.
难点:函数奇偶性的应用.
知识梳理
1.偶函数和奇函数
名师点拨
1.奇函数和偶函数的定义中的“任意”是指定义域中所有的实数;因为-x与x同时属于定义域,即具有奇偶性的函数的定义域关于原点对称.
2.函数f(x)是偶函数 对定义域内任意一个x,有f(-x)-f(x)=0 f(x)的图像关于y轴对称.
3.函数f(x)是奇函数 对定义域内任意一个x,有f(-x)+f(x)=0 f(x)的图像关于原点对称.
【做一做1-1】
若函数y=f(x),x∈[-1,a](a>-1)是奇函数,则a等于( )
A.-1 B.0 C.1 D.无法确定
答案:C
【做一做1-2】
下列函数是偶函数的是( )
A.y=2x B.y=2x2+3
解析:由偶函数的定义知,y=2x2+3是偶函数.
答案:B
2.奇偶性
归纳总结
基本函数的奇偶性如下:
【做一做2-1】 下列图像表示的函数中,具有奇偶性的是( )
解析:图像关于原点对称时,函数为奇函数;图像关于y轴对称时,函数为偶函数.从而判断选项B正确.
答案:B
【做一做2-2】 若函数f(x)=x2-2mx+4是偶函数,则实数m= .
答案:0
剖析
理解函数的奇偶性
函数f(x)的奇偶性的定义是用f(-x)=±f(x)来刻画函数f(x)的图像的特征(图象关于原点或y轴对称)的;函数的奇偶性是对于函数的整个定义域来说的,这一点与函数的单调性不同.从这个意义上来讲,函数的单调性是函数的局部性质,而奇偶性是函数的整体性质.只有对函数f(x)的定义域内的每一个值x,都有f(-x)=f(x)或f(-x)=-f(x),才能说f(x)为偶函数或奇函数;定义中要求“对于函数f(x)的定义域内任意一个自变量x,都有f(-x)=f(x)或f(-x)=-f(x)”成立,其前提为f(-x)和f(x)都有意义,所以-x也属于f(x)的定义域,即自变量x的取值范围要关于原点对称,于是奇(偶)函数的定义域是一个关于原点对称的数集,这是函数存在奇偶性的前提.例如将函数f(x)=x2+1,f(x)=x的定义域分别限定为(0,+∞)与(-3,3],则它们都为非奇非偶函数;函数奇偶性的定义中的等式f(-x)=-f(x)(或f(-x)=f(x))是其定义域上的恒等式,而不是对部分x成立.
尽管当|x|≤1时,都有f(-x)=f(x),但当|x|>1时,f(-x)≠f(x),所以它不是偶函数.
常考题型
一、判断函数的奇偶性
【例1】 判断下列函数的奇偶性:
分析:先求出定义域,再判断f(-x)与f(x)的关系.
解:(1)因为函数的定义域为{x|x≠-1},不关于原点对称,所以f(x)既不是奇函数又不是偶函数.
(2)因为函数的定义域为R,关于原点对称,
f(-x)=(-x)3-2(-x)=2x-x3=-f(x),所以f(x)是奇函数.
(3)因为函数的定义域为R,关于原点对称,
所以f(x)是偶函数.
【变式训练1】 判断下列函数的奇偶性:
(1)f(x)=x2+1,x∈[-2,2);(2)f(x)=|x-1|+|x+1|;(3)f(x)=0,x∈R.
解:(1)∵f(x)的定义域[-2,2)不关于原点对称,
∴f(x)既不是奇函数又不是偶函数.
(2)f(x)的定义域为R,关于原点对称,
又f(-x)=|-x-1|+|-x+1|=|x+1|+|x-1|=f(x),
∴f(x)为偶函数.
(3)∵f(x)=0,x∈R,
∴f(-x)=f(x),且f(-x)=-f(x),
∴f(x)既是奇函数又是偶函数.
二、奇(偶)函数的图像问题
分析:先证明f(x)是偶函数,再依据其图像关于y轴对称作图.
则f(x)的图像关于y轴对称,其图像如图所示.
解题归纳
利用函数的奇偶性作图,其依据是奇函数的图像关于原点对称,偶函数的图像关于y轴对称.
【变式训练2】 已知奇函数f(x)的定义域为[-5,5],其y轴右侧图像如图所示,写出使f(x)>0的x的取值集合.
解:由于f(x)为奇函数,y轴右侧图像已知,结合奇函数图象关于原点对称,作出y轴左侧图像,如图所示,由图像知,当x∈(0,2)时,f(x)>0;当x∈(-5,-2)时,f(x)>0,所以使f(x)>0的x的取值集合为(-5,-2)∪(0,2).
三、利用函数的奇偶性求参数
【例3】 已知函数f(x)=(x+a)(x-4)为偶函数,则实数a= .
解析:因为函数f(x)为偶函数,所以f(-x)=f(x),即(-x+a)(-x-4) =(x+a)(x-4),即x2+(4-a)x-4a=x2-(4-a)x-4a,故4-a=-(4-a),解得a=4.
答案:4
反思
利用函数奇偶性求参数值的常见类型及求解策略:
(1)定义域含参数:奇(偶)函数f(x)的定义域为[a,b],根据定义域关于原点对称,可以利用a+b=0求参数.
(2)解析式含参数:根据f(-x)=-f(x)或f(-x)=f(x)列式,比较系数可解.
【变式训练3】 若函数f(x)=ax2+bx+3a+b是偶函数,定义域为[a-1,2a],则a= ,b= .
解析:因为偶函数的定义域关于原点对称,所以a-1=-2a,
结合偶函数图像的特点,易得b=0.
四、利用函数的奇偶性求函数的解析式
【例4】 若f(x)是定义在R上的奇函数,当x<0时,f(x)=x(1-x),求函数f(x)的解析式.
解:∵f(x)是定义在R上的奇函数,∴f(-x)=-f(x).当x>0时,-x<0,
∴f(x)=-f(-x)=x(1+x).
当x=0时,f(-0)=-f(0),即f(0)=-f(0),∴f(0)=0.
反思
1.若f(x)是奇函数,且f(0)有意义,则f(0)=0;
2.已知函数的奇偶性和函数在某区间上的解析式,求该函数在与已知区间关于原点对称的区间上的解析式时,首先设出所求区间上的自变量,利用奇、偶函数的定义域关于原点对称的特点,把它转化到已知解析式的区间上,代入已知的解析式,然后再次利用函数的奇偶性求解即可.
【变式训练4】 已知f(x)是R上的偶函数,当x∈(0,+∞)时,f(x)=x2+x-1,求当x∈(-∞,0)时,f(x)的解析式.
解:设x<0,则-x>0.
∴f(-x)=(-x)2+(-x)-1=x2-x-1.
∵函数f(x)是偶函数,∴f(-x)=f(x).
∴当x∈(-∞,0)时,f(x)=x2-x-1.
小结
两个知识点:
1.偶函数和奇函数 ;2.奇偶性.
四种题型:
1.判断函数的奇偶性;
2.奇(偶)函数的图像问题;
3.利用函数的奇偶性求参数;
4.利用函数的奇偶性求函数的解析式.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
